三電平逆變器驅(qū)動(dòng)的IPMSM模型預(yù)測電流控制系統(tǒng)研究

賈紅云 李明陽

1 南京信息工程大學(xué) 自動(dòng)化學(xué)院,南京,210044 2 南京信息工程大學(xué) 大氣環(huán)境與裝備技術(shù)協(xié)同創(chuàng)新中心,南京,210044

0 引言

內(nèi)置式永磁同步電機(jī)(Interior Permanent Magnet Synchronous Motor,IPMSM)憑借其功率因數(shù)高、結(jié)構(gòu)簡單、體積小和轉(zhuǎn)矩慣性比大等優(yōu)點(diǎn),在電動(dòng)汽車和航空航天等領(lǐng)域獲得廣泛的應(yīng)用[1-2]．三電平逆變器作為多電平逆變器研究的基礎(chǔ),因輸出電平數(shù)比傳統(tǒng)的兩電平逆變器多一個(gè),因此相較于兩電平逆變器,輸出電壓電流波形正弦度更好,所含諧波分量更少,且每相橋臂上每個(gè)功率管承受的電壓更小,適合應(yīng)用在高壓大容量場合[3-4]．

模型預(yù)測控制(Model Predictive Control,MPC)根據(jù)是否考慮變換器的離散特性分為有限控制集MPC(Finite-Control-Set Model Predictive Control,FCS-MPC)[5-6]和連續(xù)控制集MPC(Continuous-Control-Set Model Predictive Control,CCS-MPC)[7-8]．CCS-MPC中的控制量是通過脈寬調(diào)制(Pulse Width Modulation,PWM)的方式作用給受控對(duì)象的,導(dǎo)致功率管的開關(guān)頻率和開關(guān)損耗增大.文獻(xiàn)[9-11]利用CCS-MPC代替矢量控制電流環(huán)的比例積分控制器,顯著加快了系統(tǒng)動(dòng)態(tài)調(diào)節(jié)過程和電流的響應(yīng)速度．FCS-MPC根據(jù)逆變器每相橋臂開關(guān)狀態(tài)所構(gòu)成的空間電壓矢量的有限性,遍歷每一個(gè)空間電壓矢量,選擇使價(jià)值函數(shù)取值最小的電壓空間矢量作為控制量．FCS-MPC具有約束條件處理簡單、多變量控制、動(dòng)態(tài)響應(yīng)快速等優(yōu)點(diǎn),但是因?yàn)榭臻g電壓矢量的數(shù)目是有限的,而且方向和幅值固定,導(dǎo)致輸出電流脈動(dòng)較大．文獻(xiàn)[12]對(duì)FCS-MPC在電力電子系統(tǒng)中的發(fā)展前景進(jìn)行了分析;文獻(xiàn)[13]把逆變器作為研究對(duì)象,針對(duì)傳統(tǒng)單矢量模型預(yù)測控制提出滯后補(bǔ)償?shù)目刂撇呗裕壳?FCS-MPC已由傳統(tǒng)單矢量MPC控制向多矢量MPC控制發(fā)展．

本文中電機(jī)控制系統(tǒng)電流環(huán)采用單矢量模型預(yù)測電流控制(Model Predictive Current Control,MPCC),并對(duì)三電平逆變器驅(qū)動(dòng)的IPMSM-MPCC系統(tǒng)進(jìn)行研究．首先對(duì)內(nèi)置式永磁同步電機(jī)數(shù)學(xué)模型、預(yù)測電流算法進(jìn)行介紹,然后對(duì)延遲補(bǔ)償算法、三電平逆變器拓?fù)浣Y(jié)構(gòu)及其空間矢量表示進(jìn)行分析,最后用Matlab/Simulink建立控制系統(tǒng)仿真模型,仿真結(jié)果表明:相比于傳統(tǒng)兩電平逆變器驅(qū)動(dòng)的IPMSM-MPCC控制系統(tǒng),三電平逆變器驅(qū)動(dòng)的IPMSM-MPCC輸出電流諧波

含量較小,系統(tǒng)的動(dòng)靜態(tài)性能較好．

1 IPMSM數(shù)學(xué)模型

本文選用內(nèi)置式永磁同步電機(jī)作為控制對(duì)象．在不計(jì)電機(jī)中的磁滯損耗、渦流損耗和電機(jī)鐵芯飽和的情況下,電機(jī)在同步旋轉(zhuǎn)坐標(biāo)系(d-q)下的定子電壓方程為

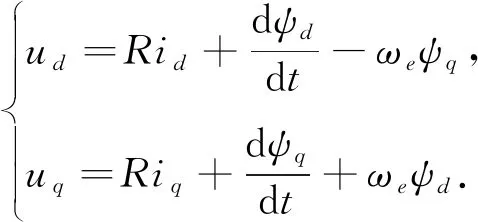
(1)

電機(jī)的定子磁鏈方程為

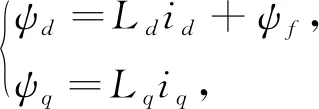
(2)

其中:id和iq分別是定子電流的直、交軸分量;R為定子電阻;ψd和ψq分別是定子磁鏈直、交軸分量;ud和uq分別為定子電壓直、交軸分量;Ld和Lq分別為定子電感的直、交軸分量;ψf為轉(zhuǎn)子永磁體磁鏈；ωe是電機(jī)旋轉(zhuǎn)的電角速度．

根據(jù)式(1)和式(2)可得電機(jī)在同步旋轉(zhuǎn)坐標(biāo)系下的定子電流狀態(tài)方程:

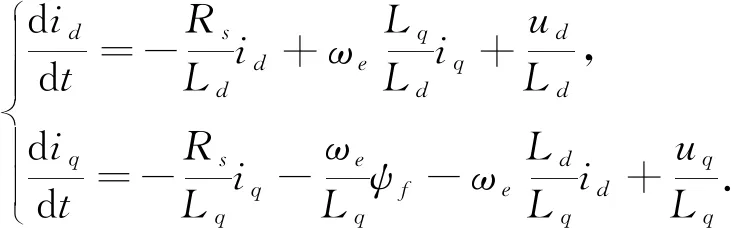
(3)

令Ts為采樣周期,對(duì)式(3)進(jìn)行一階歐拉離散化得預(yù)測電流公式為

(4)

式中:id(k+1|k)和iq(k+1|k)分別為在k時(shí)刻對(duì)直、交軸電流k+1時(shí)刻的預(yù)測值;id(k)和iq(k)分別為當(dāng)前時(shí)刻的直、交軸電流采樣值．

2 三電平逆變器拓?fù)浣Y(jié)構(gòu)及空間矢量表示

圖1為二極管鉗位型三電平逆變器拓?fù)浣Y(jié)構(gòu)．由圖1可以看出每個(gè)橋臂都由4個(gè)功率開關(guān)管、2個(gè)串聯(lián)的鉗位二極管以及4個(gè)續(xù)流二極管組成,與直流電源并聯(lián)的2個(gè)電容C1、C2用于均壓．

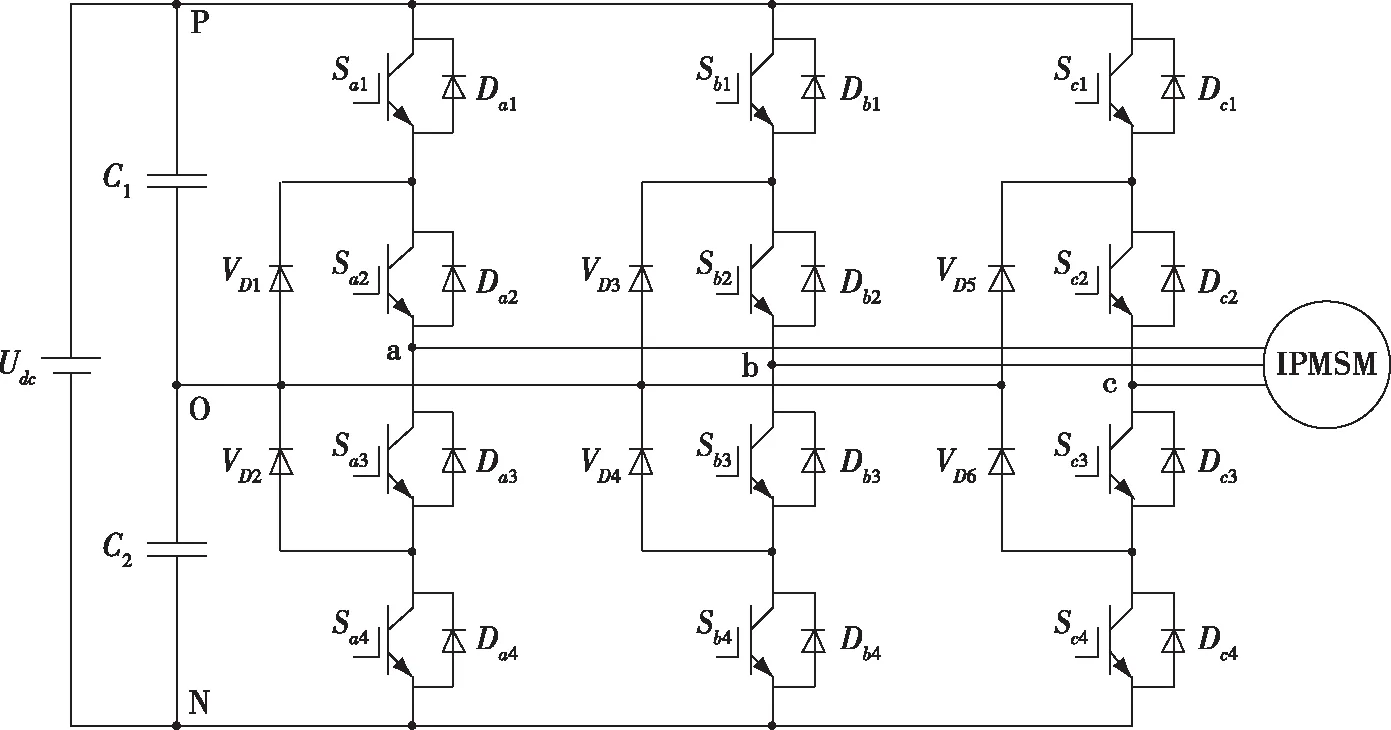
圖1 二極管鉗位型三電平逆變器拓?fù)浣Y(jié)構(gòu)Fig.1 Topology of diode clamped three-level inverter

根據(jù)功率開關(guān)管的開關(guān)次序,每個(gè)橋臂可以得到正、零和負(fù)3種電平,對(duì)應(yīng)的開關(guān)狀態(tài)分別用字母P、O和N表示．以A相為例,定義導(dǎo)通狀態(tài)為1,關(guān)斷狀態(tài)為0,當(dāng)Sa1=Sa2=1,Sa3=Sa4=0時(shí),定為P狀態(tài),輸出電壓為Udc/2;當(dāng)Sa2=Sa3=1,Sa1=Sa2=0時(shí),定為O狀態(tài),輸出電壓為0;當(dāng)Sa1=Sa2=0,Sa3=Sa4=1時(shí),定為N狀態(tài),輸出電壓為-Udc/2．為最大化降低開關(guān)損耗,每次的電壓矢量變化,只能有一相橋臂電路狀態(tài)改變．Sa1和Sa4不能同時(shí)導(dǎo)通,且Sa1和Sa3,Sa2和Sa4工作狀態(tài)是互補(bǔ)的．每相橋臂有3種開關(guān)狀態(tài),則3個(gè)橋臂就可構(gòu)成33=27種開關(guān)狀態(tài),對(duì)應(yīng)著27個(gè)電壓矢量．圖2為三電平逆變器的電壓空間矢量分布．

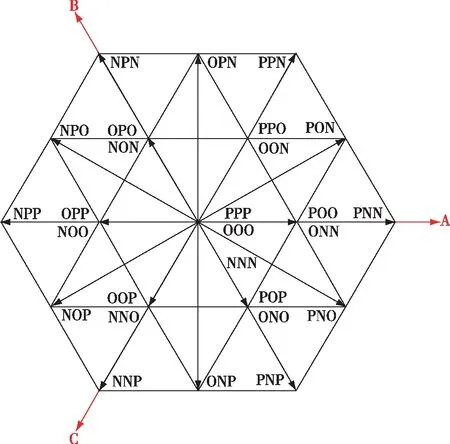
圖2 三電平逆變器的電壓空間矢量分布Fig.2 Voltage space vector distribution of three-level inverter

以A相為例,定義P狀態(tài)時(shí)Sa=1,O狀態(tài)時(shí)Sa=0,N狀態(tài)時(shí)Sa=-1,則這27個(gè)空間電壓矢量(19種不同的電壓矢量)的計(jì)算公式為

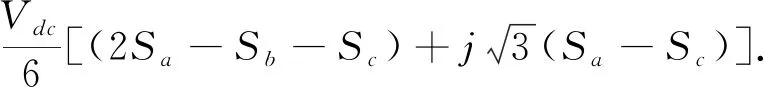
(5)

3 單矢量模型預(yù)測電流控制

MPCC是根據(jù)當(dāng)前時(shí)刻采集到的定子電流和轉(zhuǎn)速的信息,再結(jié)合電機(jī)數(shù)學(xué)模型,預(yù)測出每個(gè)電壓矢量對(duì)應(yīng)下一時(shí)刻的電流值,然后通過目標(biāo)函數(shù)取值最小的電壓矢量作用給逆變器(圖3)．

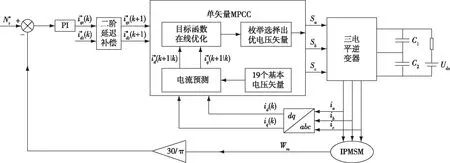
圖3 單矢量MPCC控制系統(tǒng)原理Fig.3 Schematic diagram of single vector MPCC control system

三電平中性點(diǎn)鉗位逆變器相比于傳統(tǒng)兩電平逆變器產(chǎn)生的空間電壓矢量更多,對(duì)這些所有可能的電壓矢量預(yù)測會(huì)加大系統(tǒng)的計(jì)算量．如果采樣時(shí)間足夠小的話,則有:

(6)

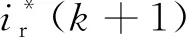
然而當(dāng)采樣周期較大時(shí),因k時(shí)刻的電流采樣值和當(dāng)前時(shí)刻開關(guān)狀態(tài)對(duì)應(yīng)時(shí)刻有延遲,所以如果采用式(6)的近似方法會(huì)造成較大的輸出紋波．針對(duì)延遲問題,采用二階拉格朗日外推預(yù)測法．該算法簡單且準(zhǔn)確性高．采用二階拉格朗日外推公式得:

(7)

(8)

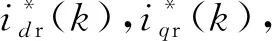
直流側(cè)的電容電壓用差分方程可表示為

(9)

(10)

分別對(duì)式(9)和(10)離散化可得:

(11)

(12)

根據(jù)式(4)、(7)和(8)可得目標(biāo)函數(shù)為

(13)

式中,λ為權(quán)值系數(shù),調(diào)節(jié)的值可以使得逆變器并聯(lián)的2個(gè)電容中點(diǎn)電壓達(dá)到平衡．

通過預(yù)測方程計(jì)算27種開關(guān)狀態(tài)對(duì)應(yīng)的空間電壓矢量下一時(shí)刻d軸和q軸電流的預(yù)測值，然后建立目標(biāo)函數(shù)，滾動(dòng)優(yōu)化選取使目標(biāo)函數(shù)值最小的電壓矢量作為最優(yōu)電壓矢量，最終產(chǎn)生最優(yōu)電壓矢量對(duì)應(yīng)開關(guān)狀態(tài)的PWM脈沖信號(hào)輸出到逆變器.圖3為三電平逆變器驅(qū)動(dòng)的PMSM單矢量模型預(yù)測控制系統(tǒng)結(jié)構(gòu).

4 仿真分析

本節(jié)對(duì)三電平逆變器驅(qū)動(dòng)的內(nèi)置式永磁同步電機(jī)MPCC進(jìn)行仿真分析(圖4),在Matlab/Simulink仿真平臺(tái)上進(jìn)行建模,IPMSM仿真參數(shù)如表1所示．

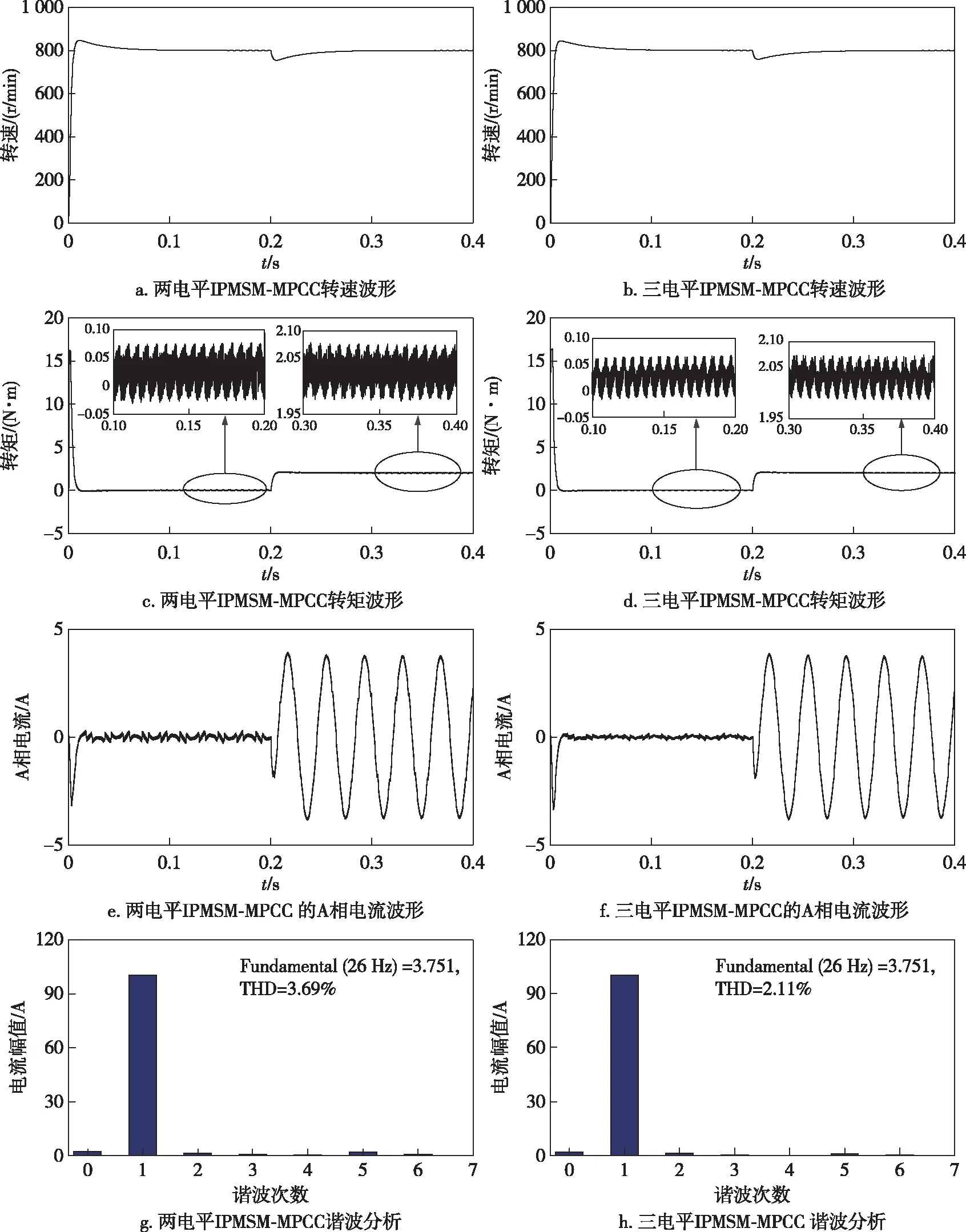
圖4 兩電平IPMSM-MPCC與三電平IPMSM-MPCC動(dòng)態(tài)響應(yīng)對(duì)比Fig.4 Comparison of dynamic response between two-level IPMSM-MPCC (left plots) and three-level IPMSM-MPCC (right plots)

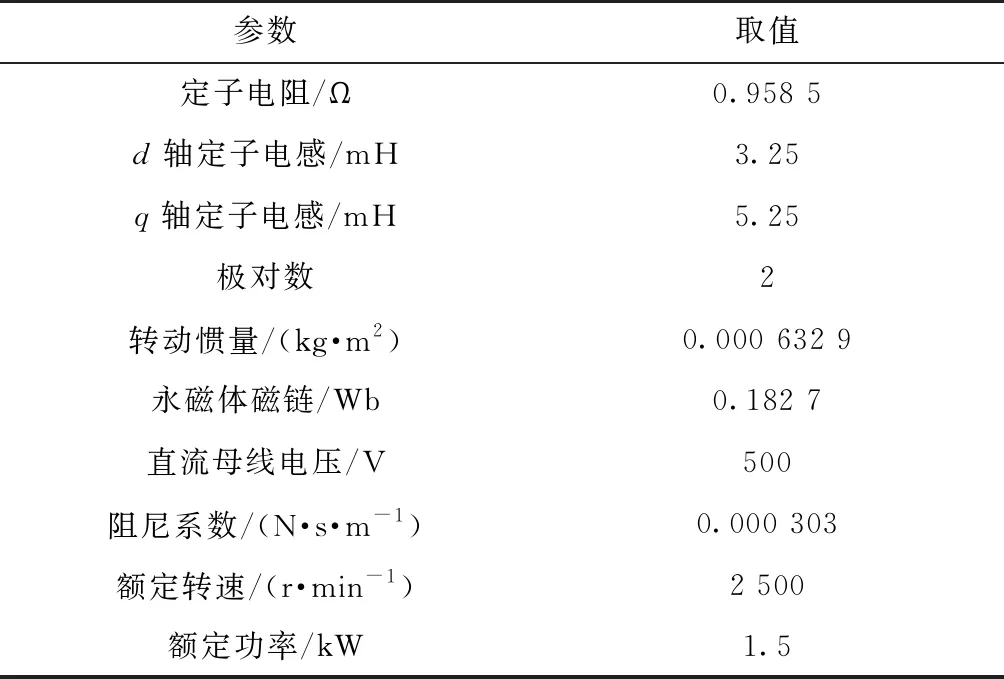
表1 IPMSM仿真參數(shù)

給定初始轉(zhuǎn)速800 r/min,空載啟動(dòng),在0.2 s突加負(fù)載轉(zhuǎn)矩2 N·m,圖4a、4c、4e、4g分別為兩電平逆變器驅(qū)動(dòng)的IPMSM-MPCC轉(zhuǎn)速、電磁轉(zhuǎn)矩、A相電流波形及其諧波分析結(jié)果，圖4b、4d、4f、4h分別為三電平逆變器驅(qū)動(dòng)的IPMSM-MPCC轉(zhuǎn)速、電磁轉(zhuǎn)矩、A相電流波形及其諧波分析結(jié)果．從圖4a和4b可以看出2個(gè)系統(tǒng)均能很好地跟蹤上參考轉(zhuǎn)速．比較圖4c和4d可以得到三電平逆變器驅(qū)動(dòng)相比于兩電平逆變器驅(qū)動(dòng)具有更好的轉(zhuǎn)矩脈動(dòng)抑制效果,更有利于在工業(yè)控制中應(yīng)用．比較圖4e、4f和圖4g、4h可以看出三電平逆變器驅(qū)動(dòng)的IPMSM-MPCC輸出的電流含諧波比兩電平逆變器驅(qū)動(dòng)的系統(tǒng)低1.58個(gè)百分點(diǎn),因此前者電流諧波程度更低、正弦度更好．

給定初始轉(zhuǎn)速800 r/min,空載啟動(dòng),在0.2 s突加負(fù)載轉(zhuǎn)矩20 N·m,圖5a和5b分別為兩電平逆變器驅(qū)動(dòng)的IPMSM-MPCC和三電平逆變器驅(qū)動(dòng)的IPMSM-MPCC線電壓Uab的波形,通過比較可得出后者系統(tǒng)的線電壓更加穩(wěn)定,波形正弦度更好,且因?yàn)楹笳呤侨娖綘顟B(tài),所以相比于兩電平逆變器驅(qū)動(dòng)更有利于減小轉(zhuǎn)矩脈動(dòng)．

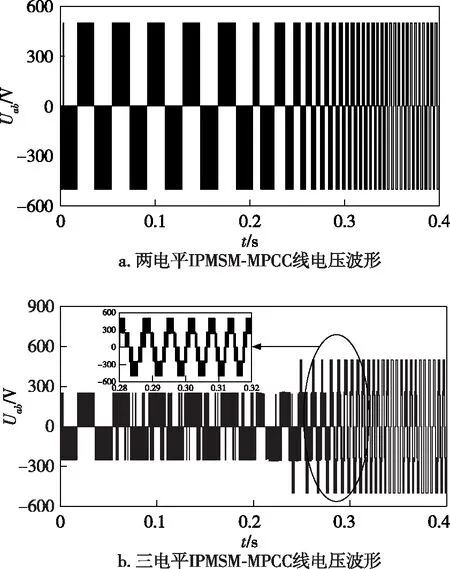
圖5 兩電平IPMSM-MPCC與三電平IPMSM-MPCC線電壓對(duì)比Fig.5 Comparison of line voltage between two-level IPMSM-MPCC (a) and three-level IPMSM-MPCC (b)

5 結(jié)語

本文對(duì)二極管鉗位型三電平逆變器驅(qū)動(dòng)的IPMSM-MPCC系統(tǒng)進(jìn)行研究分析,利用MATLAB/Simulink建立系統(tǒng)仿真模型,并分別對(duì)三電平逆變器驅(qū)動(dòng)的IPMSM-MPCC系統(tǒng)和兩電平逆變器驅(qū)動(dòng)的IPMSM-MPCC系統(tǒng)進(jìn)行對(duì)比分析,經(jīng)對(duì)比驗(yàn)證,相比于兩電平逆變器驅(qū)動(dòng)系統(tǒng),前者輸出的電壓電流波形正弦度更好,含諧波分量更少,對(duì)電機(jī)轉(zhuǎn)矩脈動(dòng)的抑制更好,單個(gè)開關(guān)管所承受的電壓應(yīng)力更小,更適合應(yīng)用在高電壓大容量場合,適合向工業(yè)控制領(lǐng)域推廣．