全自動食品售賣機機械振動控制方法

郝軍，丁澤慶

1.駐馬店技師學院（駐馬店 463000）；2.南陽技師學院（南陽 473000）

機械振動會影響自動售貨機的工作效率。為解決這個問題，科學家們通過多種方法研究如何控制振動[1-3]，如張保生等[4]設計船舶主機設備振動控制方法，根據艦船主機結構的特征，確定主機設備振動位置，為振動控制提供基礎，保證其擁有更好的減振性能，具有良好實際效果；魏春嶺等[5]在航天器姿態機動中，結合經典的Bang-Bang姿態機動指令和姿態跟蹤控制器，實施機動路徑的跟蹤，形成低頻柔性模態的振動抑制。但是，上述方法都是被動控制方法，主動性弱，主要依靠人工控制，能耗大，成本高。

對此，試驗建立所需的濾波器形式和參數，使機動后的穩定時間等效于模態振動周期，提出一種全自動食品售賣機機械振動控制方法。

1 全自動食品售賣機機械振動理論與模型優化

當自動售貨機的工作頻率與外界環境相同時，會引起自動售貨機的機械振動[6]。自動售貨機的機械振動模型屬于線彈性結構，如圖1所示。

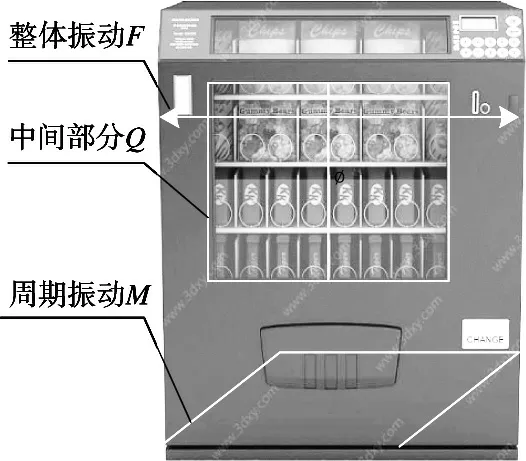
圖1 全自動食品售賣機機械振動模型

圖1 中，全自動食品售賣機在實際運行中，設備故障程度加劇時，由故障引起振動隨之加劇且一般具有一定的周期成分，當機器振動不平衡、不對中時，全自動食品售賣機的整體振動力F增強，隨機振動中的周期振動力M也會加強；與其他設備不同的是，全自動食品售賣機中間部分Q是空的，易產生共振，松動，整體不穩定性擴大，整臺全自動食品售賣機機械振動力也隨之增大。對此，利用牛頓第二定律計算出全自動食品售賣機機械振動模型每一個結構的受力情況，計算如式（1）。

式中：Mu為全自動食品售賣機的模態質量；Ku為全自動食品售賣機的模態剛度；Cu為全自動食品售賣機的模態阻尼；Fu為機電模型受到的阻力。

如果被控制的機械結構和壓電元件共同承受振動作用[7]，那么所形成的電耦合方式不同，表示為

式中：F為全自動食品售賣機在機械振動過程中產生的力；Au為全自動食品售賣機的機械動力；I為全自動食品售賣機的機械振動損失應力。

自動售貨機在運行過程中，經常會產生機械能、動能等多種能量，根據能量守恒定律，計算全自動食品售賣機機械結構電耦合方式，提高自動售貨機各部件的能耗，從而達到控制自動售貨機振動頻率，提高控制效果的目的。

2 全自動食品售賣機結構響應分析

將自動售貨機其離散化可得到自動售貨機結構系統的動平衡方程[8-9]，表示為

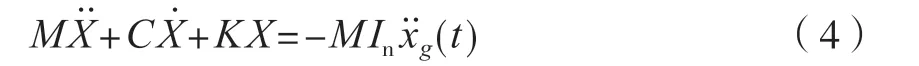
式中：M為全自動食品售賣機的體系質量；C為阻尼；K為全自動食品售賣機剛度矩陣；為全自動食品售賣機結構體系相對地面的加速度；為全自動食品售賣機結構體系運動速度；X為位移向量，In為位移影響向量；為地面水平運動在t時刻的運動加速度。

計算全自動食品售賣機結構體系在振動的瞬時過程中，給定的初始條件，即

式中：X0為全自動食品售賣機結構體系的位移；為全自動食品售賣機結構體系的速度，利用直接積分法在時域內，獲取全自動食品售賣機結構體系在t1時刻的位移和加速度等信息。利用上述計算過程，可以獲取到和Xt在t時刻的參數值，從而推導出和時刻的參數值。

如果全自動食品售賣機在振動過程中的加速度在[t,t+Δt]區間內為線性變化，通過導入控制參數θ[10]，可以得到振動加速度在[t,t+θΔt]內也是線性變化。

假設0≤τ≤θΔt，根據振動過程中的加速度假設條件可以得到，全自動食品售賣機在振動過程中的加速度向量在[t,t+θΔt]范圍內，可以描述為

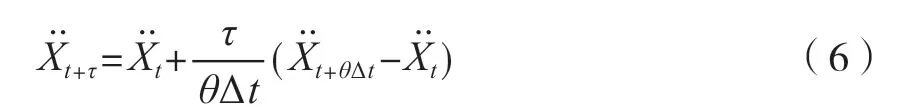
τ=θΔt時，積分處理式（7），可以得到

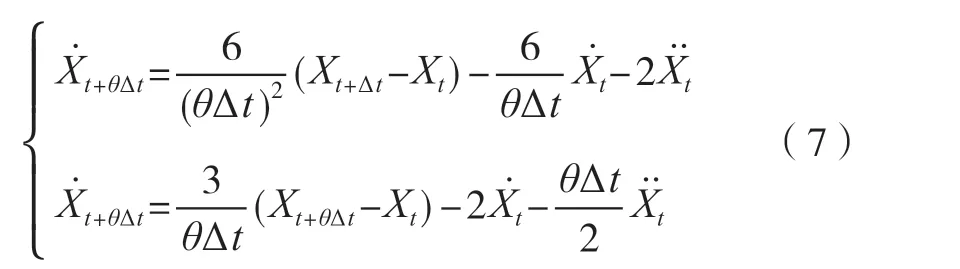
全自動食品售賣機在t+θΔt時刻發生振動時，其結構體系的動力學方程可以描述為

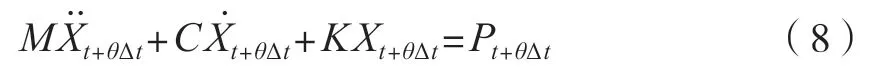
式中：Pt+θΔt為全自動食品售賣機在振動過程中的外載荷向量，Pt+θΔt=-MInxg（t+Δt）為振動等效荷載。將式（7）代入到式（8）中，可以得到一個關于Vt+θΔt的表達式，為

在全自動食品售賣機振動的頻域范圍內，可以對全自動食品售賣機結構體系的動力學方程進行傅里葉變換處理[11]，可以得到

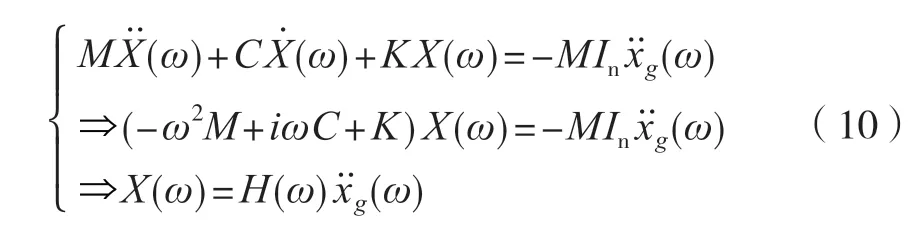
式中：H(ω)為全自動食品售賣機結構體系位移相對于的頻率傳遞函數矩陣，根據全自動食品售賣機的隨機振動思想[12]，其相對位移功率密度函數矩陣可以描述為

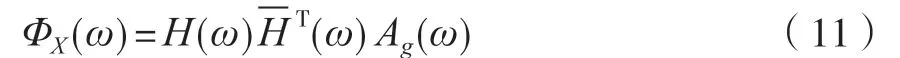
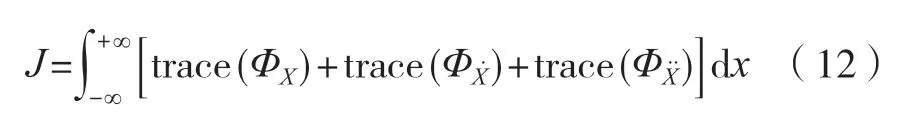
通過對自動售貨機結構系統的離散化，建立自動售貨機結構系統的動平衡方程。

根據給定的初始條件和全自動食品售賣機的振動原理，計算自動售貨機在振動過程中的加速度，并對自動售貨機結構系統的動力學方程進行傅立葉變換處理，完成自動售貨機結構系統的機械振動響應分析。

3 全自動食品售賣機機械振動控制

分析自動售貨機結構系統在機械振動作用下的非線性信號。采用經驗模態分解方法將非線性信號分解為固有模態函數，在變換之前，假設機械振動信號的每1個采樣間隔對應于1個頻率值，采用Hilbert變換處理每一個固有模態函數分量yj(t)，可以得到

式中：cj(t)為第j個采樣點的固有模態函數，P為柯西主值，yj(t)與cj(t)之間形成共軛時，就可以獲得解析信號，即

其中，Aj(t)為第j個固有模態函數分量的信號振幅；θj(t)為相位角，i為全自動食品售賣機的結構體系層數。與解析信號Zj(t)對應的頻率表示為

利用Hilbert變換可以得到全自動食品售賣機的多個固態模態函數分量[13-14]，可以將x(t)表示為

令被控制的全自動食品售賣機的機械結構具有n個自由度，在不考慮全自動食品售賣機質量和阻尼的情況下，將全自動食品售賣機結構體系的動力學平衡方程變換為

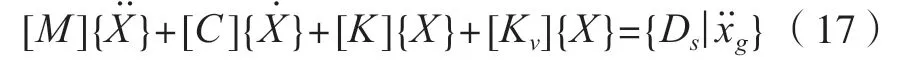
式中：Kv為全自動食品售賣機的機械結構附加剛度矩陣，Ds為機械振動作用下全自動食品售賣機的位置矩陣。通過引入狀態空間[15]，將式（17）的方程還可以變換為

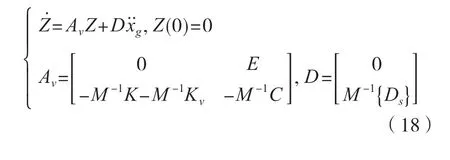
式中：Z為狀態向量，為變換處理后的狀態向量，Av為附加振幅，D為全自動食品售賣機的經過狀態變換后的位置矩陣。

完成狀態變換處理之后，假設將主動變剛度設備安裝在全自動食品售賣機機械結構的第i層，那么在全自動食品售賣機機械結構的第i層和第i-1層之間產生控制力，那么存在

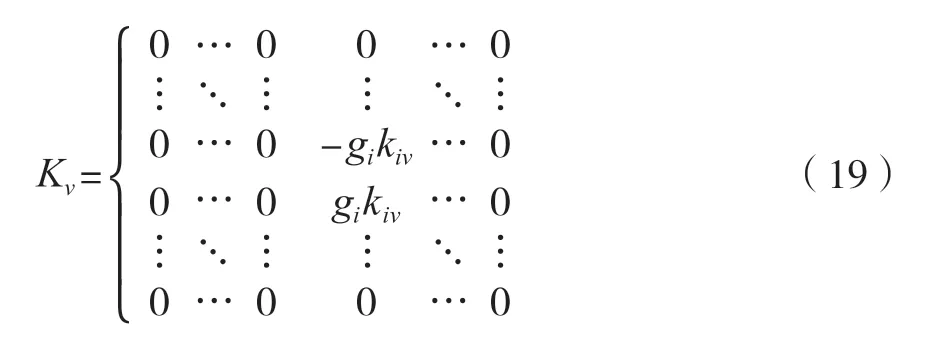
假設Pj為第j個采樣間隔時間內全自動食品售賣機的振動頻率參數值，為避免出現共軛現象，振動頻率參數值Pj接近任何一個固有頻率時，就可以通過開關函數對全自動食品售賣機的機械振動進行控制，控制過程中的切換函數為

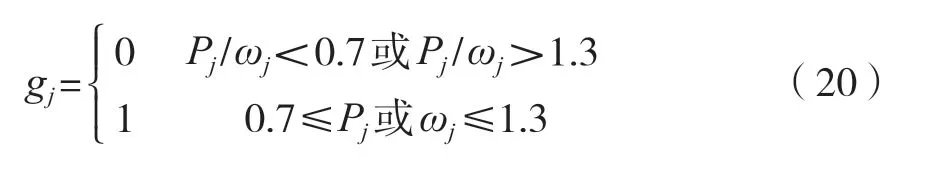
因此，利用自動售貨機的多個固態模態函數分量，對自動售貨機結構系統的動力平衡方程進行變換，并結合控制過程中的切換功能，實現自動售貨機的機械振動控制。

4 試驗對比分析

為驗證所提方法在耗電量方面的性能，分別引入文獻[4]的機械振動控制方法和文獻[5]的機械振動控制方法，作為對比方法，測試3種控制方法的機械振動控制耗電情況，結果如圖2所示。

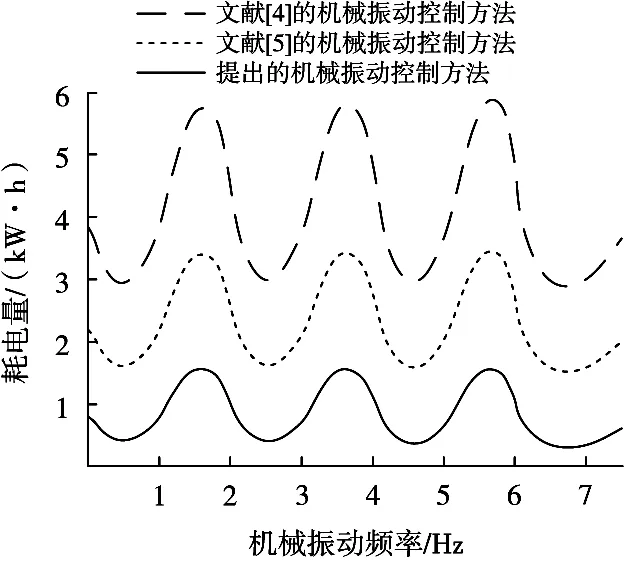
圖2 機械振動控制耗電量對比結果

從圖2的結果可以看出，文獻[4]的機械振動控制方法在規定的波動周期內，機械振動在最高點的耗電量為5.75 kW·h，文獻[5]的機械振動控制方法在規定的波動周期內，機械振動在最高點的耗電量為3.42 kW·h，而所提方法在規定的波動周期內，機械振動在最高點的耗電量為1.55 kW·h，因此可以得到，所提方法比其他2種方法的耗電量分別低73%和54.7%。

為驗證所提方法對全自動食品售賣機機械振動的控制效果，分別引入文獻[4]的機械振動控制方法和文獻[5]的機械振動控制方法，測試3種控制方法的機械振動頻率情況，結果如圖3所示。

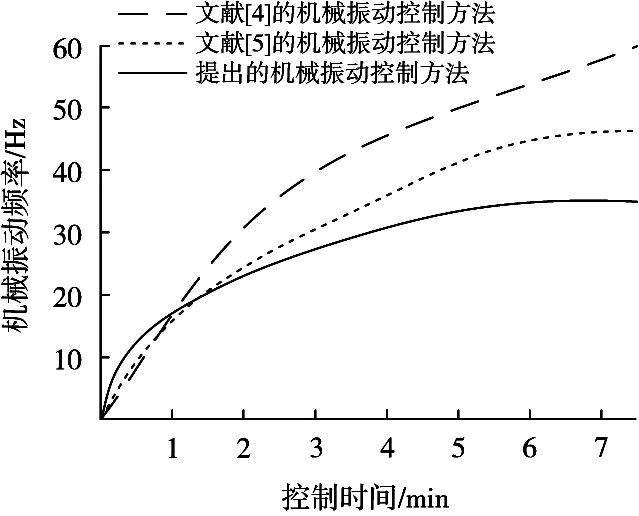
圖3 機械振動頻率情況

從圖3的結果可以看出，機械振動控制時間1 min時，3種控制方法測試得到的機械振動頻率非常接近，機械振動控制時間從第2 min開始，3種控制方法測試得到的機械振動頻率越來越快，且3種方法的差距也越來越大，由此可以得出，所提方法可以有效控制全自動食品售賣機的機械振動。

3種方法的控制能耗對比情況如圖4所示。

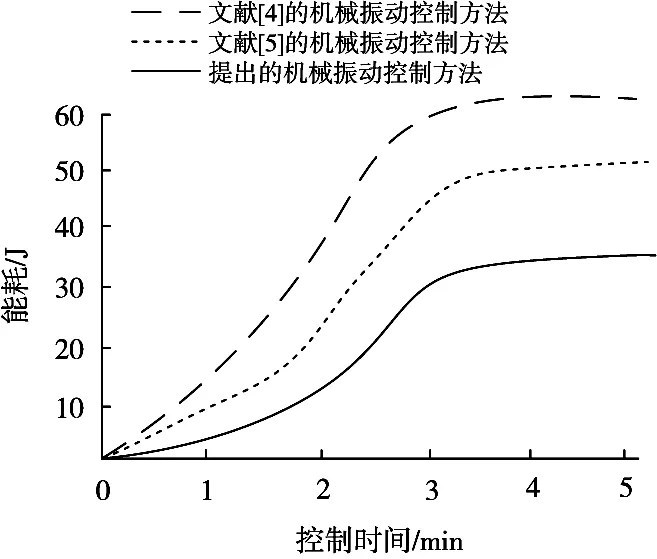
圖4 控制能耗對比情況

在測試初期，3種控制方法的能耗差距就非常大，隨著控制時間變化，文獻[4]的機械振動控制方法得到的控制能耗最高，所提方法的控制能耗最低，因此可以得到，所提方法可以降低全自動食品售賣機的機械振動控制能耗。

綜合試驗結果可以看出，在相同控制時間下，所提方法的可靠性更高。

5 結語

提出全自動食品售賣機機械振動控制方法，通過建立全自動食品售賣機機械振動理論模型，對全自動食品售賣機結構體系進行響應分析，結合全自動食品售賣機機械振動控制流程，實現全自動食品售賣機機械振動的控制。結果顯示，所提方法在耗電量、機械振動頻率和控制能耗方面，具有更高的可靠性。