基于連續-非連續方法的高填方邊坡變形穩定性分析

司憲志，寧 宇，石 崇*，黃青富，張一平

(1.河海大學 巖土工程研究所，江蘇 南京 210098；2.中國電建集團昆明勘測設計研究院有限公司，云南 昆明 650051)

我國西南地區多為山地丘陵地貌，在這些區域進行機場建造時，為制造出合適的場地條件和凈空條件，勢必會進行深挖高填工作，產生大量的高填方邊坡[1]，同時山地及丘陵地帶復雜的地質條件，也給機場建設的安全性帶來了挑戰，填方地基及高填方體的穩定性問題成為山區機場建設中存在的核心問題[2]，加強對該高填方邊坡穩定性的研究，尋求科學、合理、有效的評價及防治措施，具有重要的現實意義。數值模擬由于其成本低、效果明顯的特點被廣泛地應用于邊坡穩定性分析[3]中，在連續數值仿真方法方面：陳正東[4]等基于有限差分軟件FLAC3D軟件，建立了三維邊坡數值計算模型，研究了開挖后的邊坡體的位移變形特征，并據此對開挖后的邊坡進行了穩定性評價；潘網生[5]等基于FLAC3D拉格朗日快速差分算法模擬煤層開挖，揭示邊坡變形過程及其滑動機理；言志信[6]等以含軟弱層的錨固巖體邊坡為研究對象，利用FLAC3D軟件模擬分析了地震作用下含軟弱層巖體邊坡兩錨固界面剪切作用及其演化。但連續數值方法中單元之間需要公用節點才能合理描述荷載力的傳遞，所能模擬的變形量有限，當變形增大到一定程度時，單元會發生畸變導致剛度矩陣無法求解，導致計算終止。在非連續數值仿真方法方面：李龍起[7]等利用顆粒流軟件PFC2D對土質滑坡在持續降雨作用下的變形發展過程進行模擬研究，揭示了該滑坡的發展及破壞模式；楊忠平[8]等用振動臺物理模型試驗，結合UDEC離散元分析方法，研究了頻發微震作用下典型上覆軟弱巖體邊坡的累計損傷過程、動力響應特征及破壞模式，Hung[9]等通過有限元分析和離散元分析，探討了同震滑坡的破壞前機制和破壞后運動過程與初始時間和運動擺度相關的顯著特征。離散單元方法中塊體或顆粒可以分離，通過每個時間步不斷地接觸判斷更新塊體或顆粒的運動方程，不受變形量限制，但是大量的接觸判斷導致計算速度降低。

綜上所述，如果能將連續-非連續耦合數值模擬方法相互結合，潛在破壞區域采用非連續方法模擬，對于基巖部分變形量小不會出現大變形破壞的區域則采用連續數值模擬方法分析，則既能滿足計算效率的要求，又不受變形量限制。本文基于連續-非連續理論，通過邊界墻耦合方法建立了某高填方邊坡連續-非連續數值模型，研究了該邊坡在天然工況下攔擋壩的應力分布情況，將強度折減法應用于細觀模擬，進行了邊坡在降雨工況下的穩定性分析，并求解了邊坡的安全系數，分析了邊坡在極端工況下可能的變形破壞情況。

1 連續非連續數值模擬方法

1.1 連續-非連續邊界耦合

在連續-非連續相互耦合分析中，有限差分軟件FLAC用來從宏觀上模擬連續區域內的力學行為，而顆粒流軟件PFC用來從細觀上模擬離散區域內介質的力學行為，兩者間的相互耦合依賴于連續區域與離散區域的接觸邊界，不同區域間的計算數據是借助于Socket O/I接口來進行相互傳輸與交換[10-11]，連續-非連續耦合計算原理見圖1。

圖1 連續-非連續耦合計算原理Fig.1 Calculation principle of continuous-discontinuous coupling method

本文采用基于邊界控制墻體的連續-非連續耦合方法，在離散區域和連續區域之間創建邊界墻體，離散區域的顆粒運動過程中作用于墻體上的接觸力和接觸彎矩，采用等效力的方法分配到邊界墻體的頂點上，進而將力的信息傳遞給連續區域的單元，這些力參與到連續區域的有限差分法分析，同樣連續區域的運動也會帶動邊界墻體的運動，進而將位置和速度通過邊界墻傳遞給離散區域，由此實現離散區域與連續區域的耦合計算。

1.2 強度折減法

強度折減法通常應用于計算邊坡的安全系數，它是通過逐漸減小邊坡體材料的強度參數，從而使邊坡體進入到臨界破壞狀態來求解安全系數。對于Mohr-Coulomb破壞準則來說，安全系數F根據下面的方程來定義：

(1)

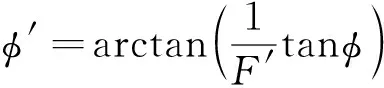
(2)

式中c′為折減后的粘聚力；φ′為折減后的內摩擦角；F′為折減系數。

通過不斷調整邊坡的巖土體強度指標，即內聚力c和內摩擦角φ，然后對邊坡進行穩定性分析，隨后通過不斷增加折減系數，進行一系列的計算直至邊坡達到極限平衡狀態，這時候得到的折減系數即為安全系數[12]。

2 工程應用

2.1 工程概況

現擬建某高填方機場，場區高差近400 m，海拔1 500～1 900 m，本期規劃機場設計標高1 743 m，挖方量約1 655×104m3，最大挖方高度約70余米，填方量約1 457×104m3，最大填方高度70余米。由于填方高度較大，存在的主要工程地質問題為高填方邊坡的穩定性問題以及不均勻沉降問題。

2.2 計算模型與條件

基于以上工程地質狀況通過FLAC3D與PFC對NPH3剖面建立連續非連續耦合模型，三維模型尺寸為280 m×8 m×162 m，如圖2所示，模型分為基巖、壩體、風化帶和土石堆積四部分。土石堆積體用離散元顆粒表示，生成顆粒33 600個，顆粒的直徑分布在0.4～0.8 m之間，土石混合體部分顆粒的孔隙率為0.55，顆粒間的接觸采用接觸粘結模型。擋土壩和基巖由于變形較小，故采用連續單元模型，由于單元的尺寸會對計算結果產生影響，網格密度越高計算結果越精細，但密度過高的網格，其計算效率也越低，為保證合理的計算效率，依據文獻[13-15]中相同尺度的模型取單元尺寸大小，單元網格尺寸應取2～5 m，本模型中取3 m，通過ANSYS劃分網格后再將模型導入FLAC3D中，共生成單元網格7 897個，單元節點12 225個，對連續區域的模型使用Mohr-Coulomb準則，模型的約束條件設置為左右兩側約束水平位移，底邊固定，模型的宏細觀參數標定如表1所示。

圖2 三維數值模型Fig.2 3D numerical model

表 1 數值模型巖土體宏細觀參數

3 結果分析

3.1 天然工況

對建立的連續-非連續耦合模型賦予表1所示的宏細觀參數，并使其在自重下平衡，最終得到的天然工況下土石堆積體力鏈分布如圖3所示，由于自重作用，堆積體底部力鏈較為粗壯，頂部力鏈相對稀疏，在堆積體和風化巖的接觸界面，由于接觸界面并不為水平，堆積體有相對滑動趨勢，但是在壩體的作用下并無位移，因此堆積體與壩體接觸部位力鏈相對粗壯，且堆積體右側力鏈出現部分張拉力鏈。天然工況下堆積體的大主應力分布

圖3 天然工況下堆積體力鏈圖Fig.3 Stacking force chain diagram under natural working conditions

如圖4所示，由于堆積體的作用，壩體左下角出現應力集中，最大主應力為3.2 MPa。

圖4 攔擋壩壩體的大主應力等值線圖Fig.4 Contour map of high principal stress of retaining dam

3.2 降雨工況

在降雨條件下，降雨過程中及降雨后雨水滲透土體邊坡，會引起坡體非飽和帶的土體基質吸力降低，由于雨水向下滲透以及地下水位的升高，會導致巖土體的容重發生變化，同時由于水對巖土體的軟化作用，使得巖土體的物理力學參數降低[16-18]，此外水會對土體產生滲流力與浮力的作用，因此邊坡體內的滲流場的變化會引起應力場的變化，同時滲流場的變化也會相應地影響到邊坡體中的應力場，水的流動與土體的變形是相互制約相互作用的，在模擬中實現降雨中應力場與滲流場的耦合過程較為復雜，因此為簡化降雨工況，將降雨過程簡化為對土石堆積體的細觀參數進行折減，表2[19-26]統計了近年來8例滑坡中土體飽和狀態及天然狀態其物理力學參數的折減百分比，土體參數的折減范圍在4%～29%，將各案例中土體參數的折減百分比通過氣泡圖來展示(圖5)，可見折減百分比大部分在10%～20%，所統計滑坡土體參數折減的平均值在15.45%左右，對于宏觀土體應對其內聚力及內摩擦角進行折減，對于土體顆粒的細觀參數，根據文獻[11，27]的研究，并依據工程經驗，應對離散顆粒間接觸的摩擦系數、接觸粘結張拉強度和接觸粘結強度折減15%。

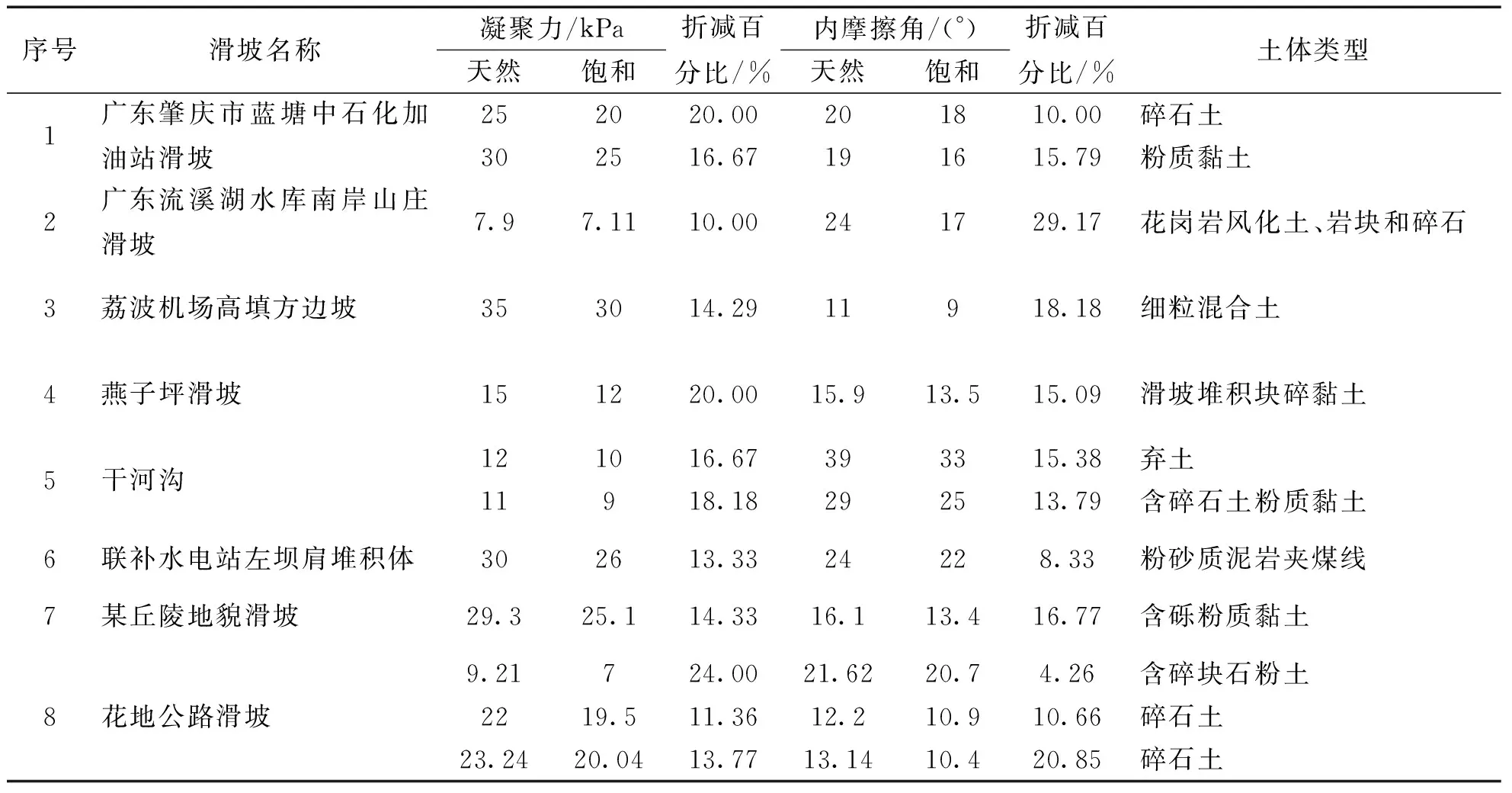
表2 滑坡體材料折減參數

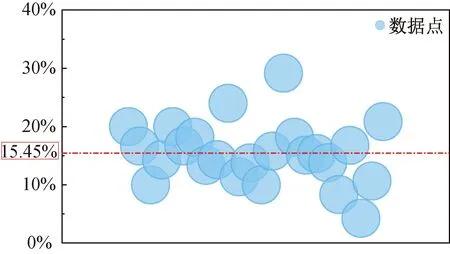
圖5 土體參數折減百分比氣泡圖Fig.5 Bubble chart of reduction percentage of soil parameters

為監測壩體以及堆積體的位移情況，在壩體背面設置監測線，沿堆積體坡面設置監測點，由于監測單獨顆粒具有一定的隨機性，因此設置數個顆粒團作為一個監測點，并取這幾個顆粒的平均位移作為測點的位移，測線及測點分布如圖6所示。

圖6 測線及測點設置Fig.6 Setup of measuring lines and points

降雨工況下壩體的位移等值線圖如圖7(a)所示，壩體位移較小，最大位移處位于壩體頂部，為3.8 mm，從壩體頂部至壩體底部位移逐漸減小，壩體背面的位移曲線如圖7(b)所示，壩體位移隨高程增加而增加，但降雨工況下位移相對較小。

圖7 降雨工況下壩體位移Fig.7 Dam displacement under rainfall condition

降雨工況下堆積體的位移如圖8(a)所示，最大位移處位于堆積體的頂部，為0.5 m。堆積體坡面沿高程方向的位移曲線如圖8(c)所示，堆積體的位移沿坡面從坡底向坡頂逐漸增加，位移與高程基本呈線性相關，出現這一現象的原因是由于降雨工況下堆積體的材料參數折減導致的不均勻沉降。由圖8(b) 可見，堆積體的位移主要朝下，在與風化帶接觸界面角度的影響下，堆積體產生少量沿坡面方向的位移，但在壩體的阻擋作用下，未產生明顯的沿坡面方向位移。

3.3 強度折減

利用強度折減法對堆積體的力學參數進行折減以尋求邊坡安全系數，對堆積體顆粒間接觸的摩擦系數、接觸粘結張拉強度和接觸粘結強度進行折減，按照二分法依次折減，若堆積體出現明顯滑動面或塌落，則判定為破壞，當折減至臨界破壞狀態，則取安全系數為讓模型恰好出現破壞的折減系數。圖8為對模型采用二分法折減時堆積體的位移云圖，當折減系數為2.0時，堆積體出現明顯塌落，并沿圖示曲線滑塌，則調整折減系數為1.50，堆積體并無明顯滑動面，繼續折減直至堆積體恰好出現破壞，如圖9(d)和圖9(f)所示，當折減系數為1.60時，堆積體恰好出現滑動面，當折減系數為1.59時，堆積體無滑動面出現，因此判定堆積體的安全系數為1.60。

圖8 降雨工況下堆積體位移Fig.8 Displacement of accumulation body under rainfall condition

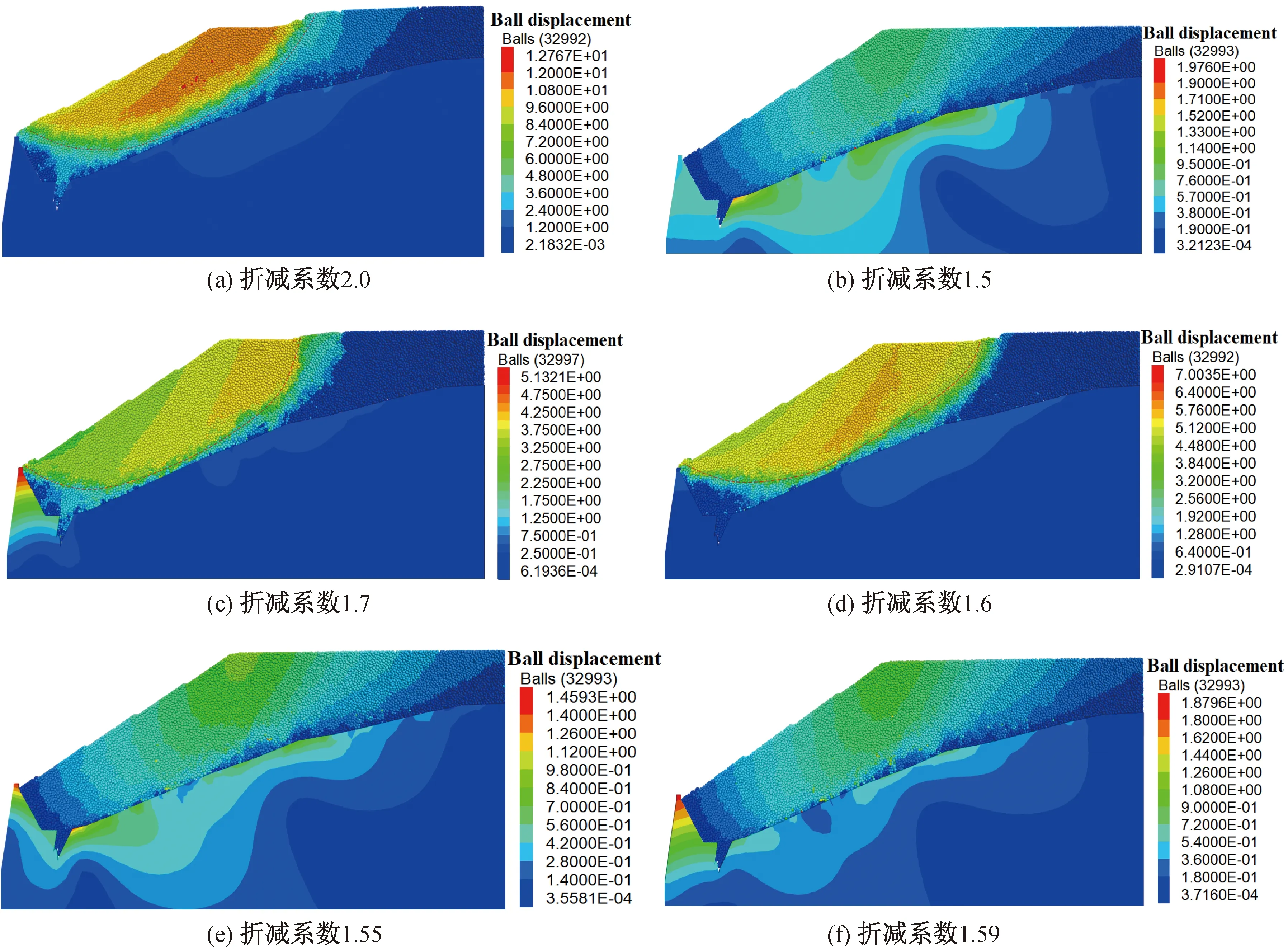
圖9 不同折減系數下堆積體位移云圖Fig.9 Displacement nephogram of accumulation under different reduction factors

當折減系數為1.60時，堆積體顆粒的位移情況如圖10(b)所示，堆積體顆粒出現塌落，并沿圖示曲線滑塌，在壩體頂端滑出，但壩體無明顯位移，顆粒的位移方向如圖10(a)所示，滑塌區域的顆粒位移方向基本一致，位移最大的區域位于滑塌體中部，堆積體顆粒的力鏈如圖10(c)所示，滑塌區域頂部(如圖所示方框內)力鏈出現斷裂，可見滑塌區域與后方堆積體出現明顯的錯動；堆積體顆粒的接觸破壞模式如圖10(d)所示，不同的接觸狀態表明不同的接觸破壞方式。從圖中接觸粘結破壞模式可以看出，堆積體的滑動面附近大部分顆粒接觸處于非粘結狀態和由剪切破壞導致的接觸非粘結狀態，產生的裂隙大部分位于滑動面附近，與實際滑坡相符合。

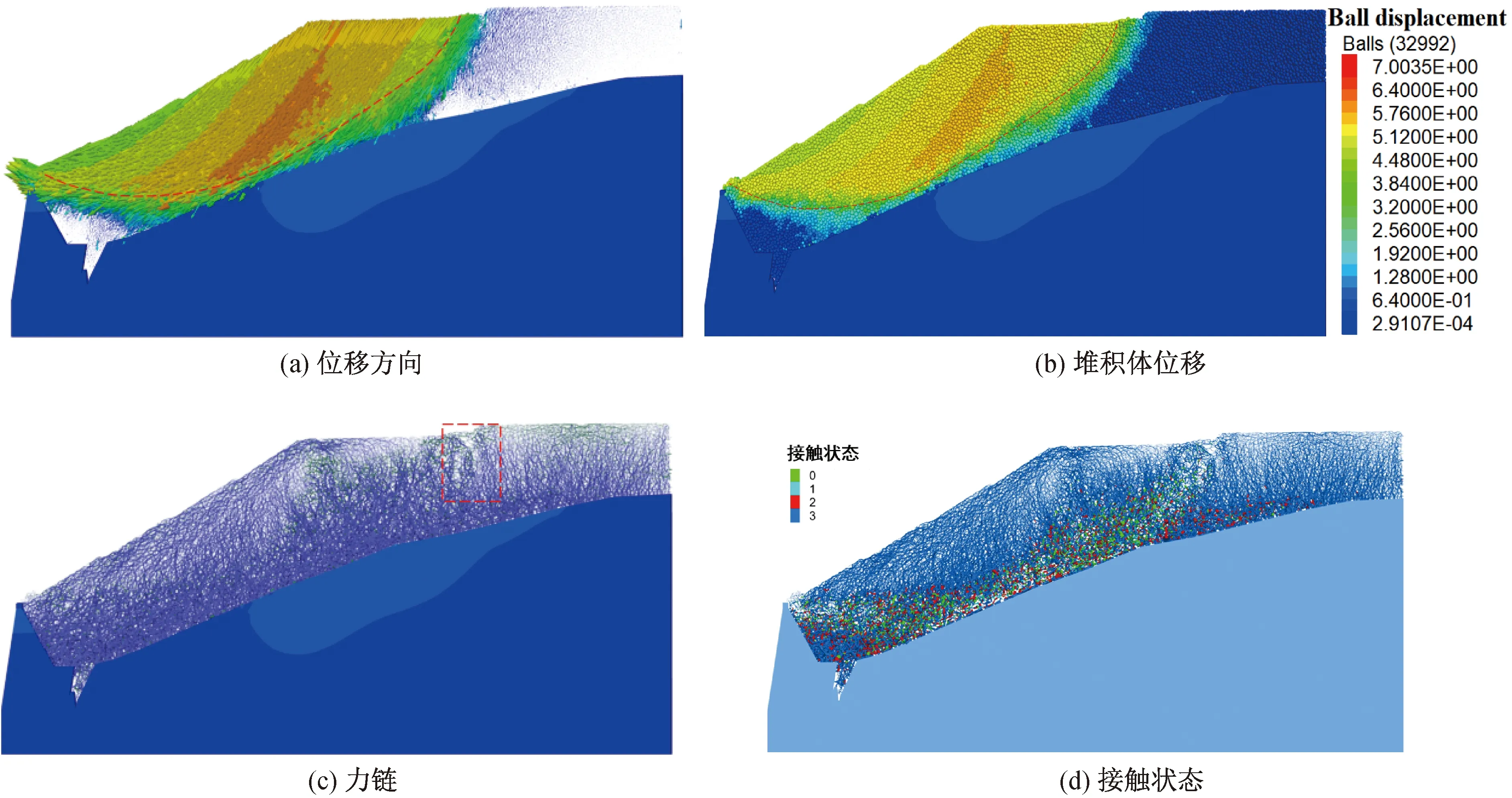
注：圖例中0表示相鄰顆粒處于非粘結狀態，1表示接觸非粘結并且是由于張拉導致破壞，2表示接觸非粘結并且是由于剪切破導致產生，3表示接觸處于粘結狀態且粘結完好無損。圖10 折減系數為1.60時顆粒情況Fig.10 Particle size distribution with reduction factor of 1.60

堆積體坡面沿高程方向的顆粒位移情況圖11所示，坡面位移最大的區域位于堆積體頂部，為3.78 m，位移最小的區域位于堆積體坡面底部，為1.64 m，除堆積體底部與壩體接觸區域外，堆積體坡面的位移基本與高程成正比，結合圖10(b)，高填方邊坡在極端情況(如持續高強度降雨、地震等)下，潛在失穩區域更大，發生失穩時滑面更深，范圍更廣，更應做好邊坡的支擋工作。

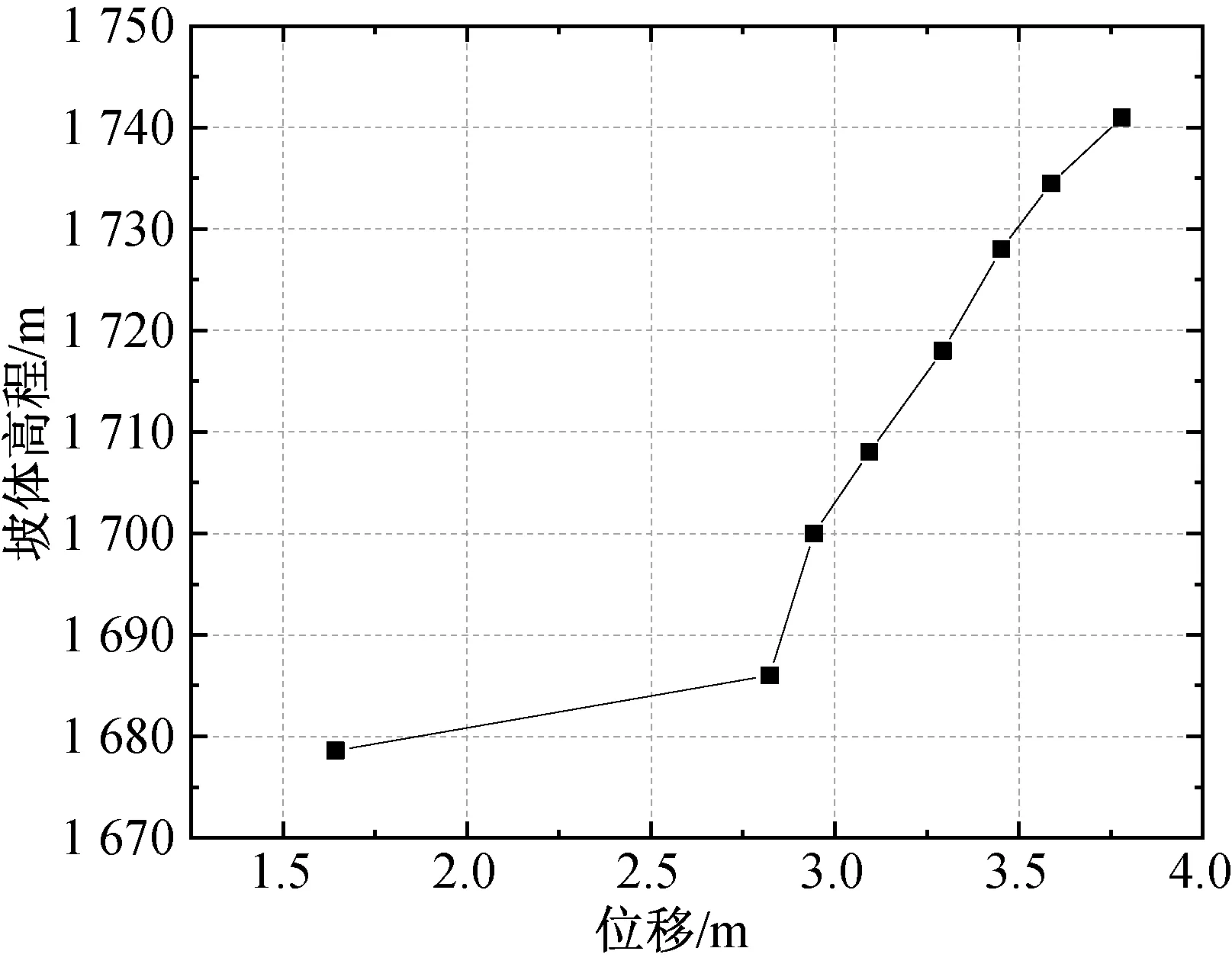
圖11 折減系數為1.60時坡面高程位移Fig.11 Elevation displacement of slope with reduction factor of 1.60

4 結論

本文基于連續-非連續耦合數值模擬方法，依據邊界墻耦合理論建立PFC-FLAC耦合模型，并通過強度折減法對邊坡進行了穩定性分析，得到結論如下：

1) 通過該方法驗證了連續-非連續耦合分析在邊坡工程中的應用可行性，運用連續-非連續方法分析可以更直觀高效地評估邊坡穩定性。

2) 通過強度折減法求解了某工程高填方邊坡的安全系數，并研究了其在降雨工況下和極端工況下的邊坡穩定性情況，得出在降雨工況下邊坡較為穩定，在極端工況下邊坡產生大范圍滑塌，滑塌區域沿壩體頂部滑出。

3) 高填方邊坡在極端工況下產生滑坡時，會產生更大的滑坡區域，更應做好對高填方邊坡的支護工作。