b-距離空間中隱性壓縮不動(dòng)點(diǎn)定理

王宏穎，賀飛

(內(nèi)蒙古大學(xué)數(shù)學(xué)科學(xué)學(xué)院，內(nèi)蒙古呼和浩特010021)

1.引言

1993年，Czerwik[1]引入了b-距離空間的概念.當(dāng)空間系數(shù)s=1時(shí)，該類空間為距離空間，因此b-距離空間是距離空間的推廣.此后許多學(xué)者將各種形式的不動(dòng)點(diǎn)定理建立到b-距離空間中，例如見文[2-4].另一方面，2011年，Berinde等人[5]在距離空間中建立了含有六元連續(xù)函數(shù)的隱性壓縮不動(dòng)點(diǎn)定理.之后，有些學(xué)者在距離空間討論并發(fā)展含有六元函數(shù)的壓縮不動(dòng)點(diǎn)定理的其他形式，例如見文[6-10].最近，Karapinar等人[11]和Aydi等人[12]定義了一類新的函數(shù)，并分別在距離空間，四角距離空間下建立了幾類隱性壓縮的不動(dòng)點(diǎn)定理.

本文在b-距離空間中建立了兩類含有六元連續(xù)函數(shù)的隱性壓縮不動(dòng)點(diǎn)定理.第一個(gè)結(jié)果將Berinde等人[5]的隱性壓縮不動(dòng)點(diǎn)定理推廣到b-距離空間.應(yīng)用我們的結(jié)果可以推出b-距離空間的Banach型，Chatterjea型，Kannan型壓縮不動(dòng)點(diǎn)定理.2015年，Dung等人[13]成功解決了Jovanovi等人[14]提出的公開問題，即將b-距離空間中經(jīng)典Banach壓縮不動(dòng)點(diǎn)定理的壓縮系數(shù)從放寬為[0，1).我們的結(jié)果也可以推出Dung等人的結(jié)果.第二個(gè)結(jié)果將距離空間中Karapinar等人[11]提出的新的Kannan型壓縮不動(dòng)點(diǎn)定理和四角距離空間中Aydi等人[12]提出的新的′Ciri′c-Reich-Rus型壓縮不動(dòng)點(diǎn)定理建立到b-距離空間，并統(tǒng)一了這兩種類型的壓縮條件.

2.預(yù)備知識(shí)與主要結(jié)果

首先我們來回顧一下b-距離空間一些基本定義和性質(zhì).

定義2.1[1]設(shè)X是一個(gè)非空集合，s≥1是給定的正實(shí)數(shù)，如果函數(shù)d:X×X→[0，∞)滿足以下條件:

(b1)d(x，y)=0，當(dāng)且僅當(dāng)x=y;

(b2)d(x，y)=d(y，x);

(b3)d(x，y)≤s[d(x，z)+d(z，y)]，

則稱d為X的b-距離，且稱(X，d)為b-距離空間，其中s稱為(X，d)的系數(shù).

顯然，b-距離空間是距離空間的推廣.

定義2.2[1]設(shè)(X，d)是系數(shù)為s≥1的b-距離空間，{xn}是X中的點(diǎn)列.

1)點(diǎn)列{xn}收斂于x∈X，當(dāng)且僅當(dāng)

2)點(diǎn)列{xn}是Cauchy列，當(dāng)且僅當(dāng)

3)空間(X，d)是完備，當(dāng)且僅當(dāng)X中的任意Cauchy列都收斂.

下面是Suzuki[15]提出的b-距離空間中的一個(gè)重要引理.進(jìn)一步，此引理可以被推廣到類擬b-距離空間中，參見文[16].

引理2.1[15]設(shè)(X，d)是系數(shù)s≥1的b-距離空間，{xn}?X.如果存在一個(gè)r∈[0，1)，使得對任意n∈N，滿足

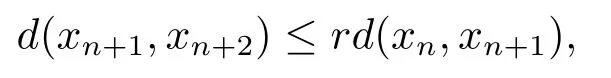
那么{xn}是一個(gè)Cauchy列.

下面介紹含有六元函數(shù)的隱性壓縮的相關(guān)概念.

設(shè)F是滿足以下兩個(gè)條件的六元實(shí)值連續(xù)函數(shù)F:→R+的集合，

(F1)F關(guān)于第五變元是非增的，且對任意s≥1，存在h∈[0，1)，滿足

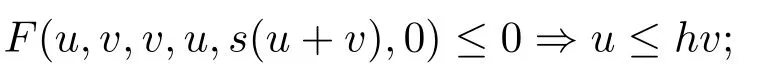
(F2)對任意的u＞0，有F(u，u，0，0，u，u)＞0.

我們給出一些滿足隱性關(guān)系的六元連續(xù)函數(shù)F的具體例子.

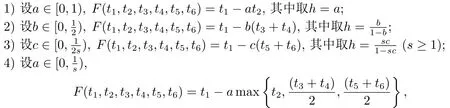
其中取h=max(s≥1);

5)設(shè)a∈[0，1)，且

6)設(shè)a∈[0，

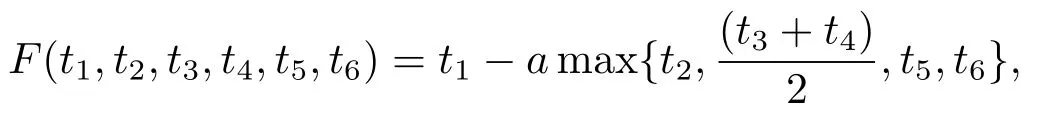
其中取h=(s≥1).

下面例子說明隱性壓縮條件中的(F1)和(F2)是相互獨(dú)立的.

本計(jì)劃第二天清晨永遠(yuǎn)離開秦川，可是現(xiàn)在，艾莉突然想在這里多住幾天。很顯然女人不過將她當(dāng)成一個(gè)試圖混進(jìn)豪宅的女孩——煮咖啡，煮牛奶，洗刷餐具，洗刷馬桶，拿不菲的薪水，住豪華的房子……然后，趁女主人不注意，與男主人調(diào)情或者偷情——艾莉相信這樣的生活對很多年輕并且貧困的女孩極具吸引力。現(xiàn)在她必須讓女人相信她是秦川買來的充氣娃娃——工廠出來的產(chǎn)品，供男人發(fā)泄性欲的玩具。她對他們的生活不會(huì)造成絲毫影響。

例2.2令a∈[0，1)，L≥0.

1)設(shè)F(t1，t2，t3，t4，t5，t6)=t1-at2-Lt6.容易證明F滿足(F1)，其中取h=a，但當(dāng)L＞1時(shí)，F(xiàn)不滿足(F2);

2)設(shè)F(t1，t2，t3，t4，t5，t6)=t1-at2-Lt3.容易證明F滿足(F2)，但當(dāng)L＞1時(shí)，F(xiàn)不滿足(F1).

例2.3設(shè)F:R6+→R+，容易驗(yàn)證下列定義的F同時(shí)滿足(F1)和(F2).

1)設(shè)λ∈[0，1)，α∈(0，1)，F(xiàn)(t1，t2，t3，t4，t5，t6)=t1-其中取h=

2)設(shè)a∈[0，1)，α，β＞0，α+β＜1，

下面給出本文第一個(gè)主要結(jié)果.

定理2.1設(shè)(X，d)是系數(shù)為s的完備b-距離空間.設(shè)T是X→X的自映射，且滿足存在F∈F，使得對任意x，y∈X，有

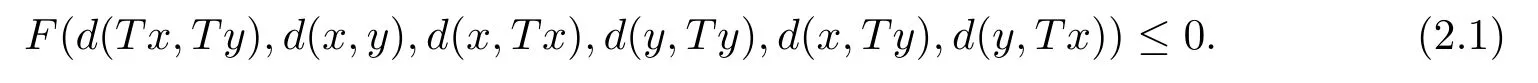
如果d連續(xù)或者T連續(xù)，那么

(a)T在X中有唯一不動(dòng)點(diǎn)x*;

(b)由xn+1=Txn，n=0，1，···定義的迭代點(diǎn)列收斂于x*;

(c)當(dāng)sh＜1時(shí)，有以下估計(jì)成立

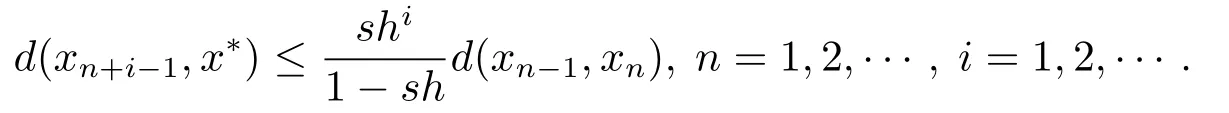
證任取x0∈X，令xn+1=Txn=Tnx0，n=0，1，2，···，由此構(gòu)造迭代點(diǎn)列{xn}.

第1步證明{xn}是Cauchy列.

由(2.1)式可得

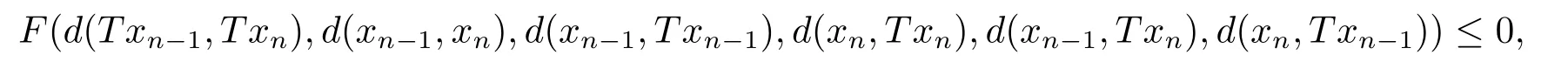
即

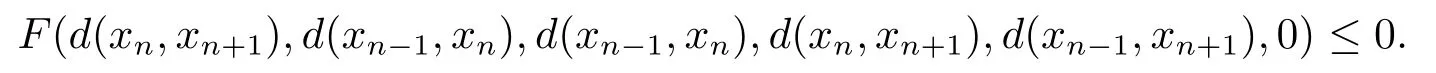
由b-距離空間的三角不等式可得

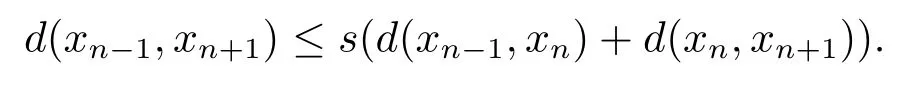
由于F滿足條件(F1)且關(guān)于第五變元是非增的，故

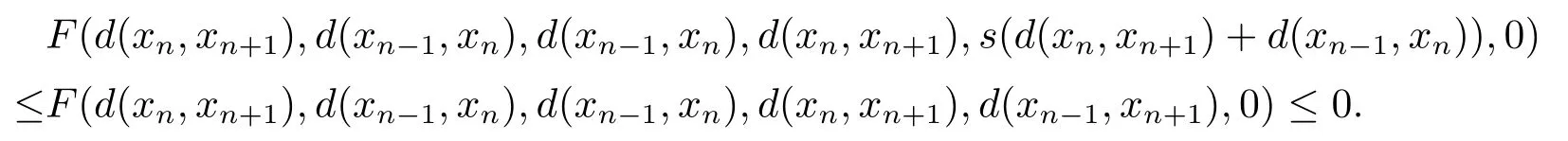
由F滿足條件(F1)可知，存在h∈[0，1)，使得

由(2.2)和引理2.1可得，{xn}是X中Cauchy列.又由于X是完備的，故存在x*∈X，使得

此時(shí)結(jié)論(b)得證.

第2步證明x*為T的不動(dòng)點(diǎn).

以下分d連續(xù)和T連續(xù)兩種情況證明.

情況1若d有連續(xù)性.

由(2.1)可得

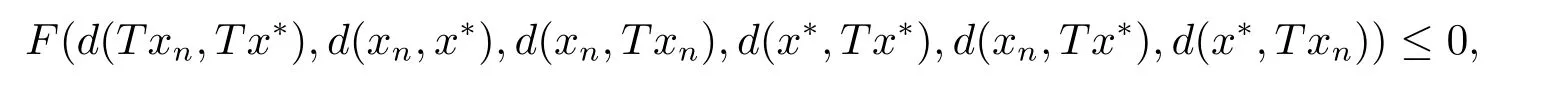
即

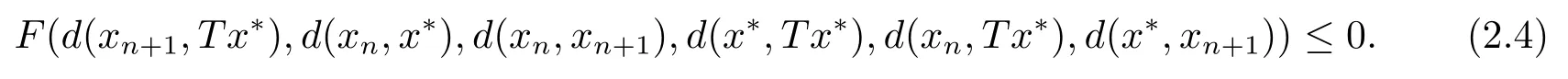
對(2.4)兩邊同時(shí)取極限，由F和d的連續(xù)性可得

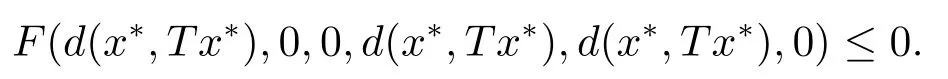
由于F關(guān)于第五變元是非增的，故

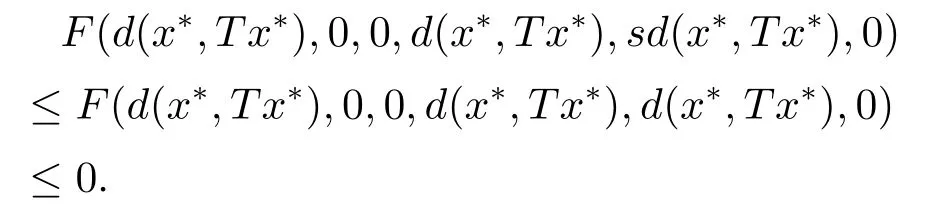
由上式和F滿足條件(F1)可知，存在h∈[0，1)，使得d(x*，Tx*)≤h0=0，即x*=Tx*.

情況2若T是連續(xù)的.

由(2.3)和T的連續(xù)性可得

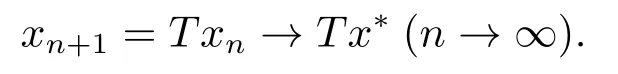
由于極限的唯一性，故x*=Tx*.

第3步證明不動(dòng)點(diǎn)的唯一性.

反證法，假設(shè)T存在另一個(gè)不動(dòng)點(diǎn)y*且x*y*，則d(x*，y*)＞0.由(2.1)可得

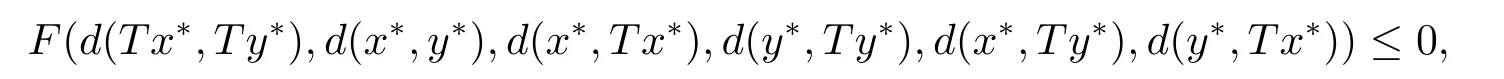
即

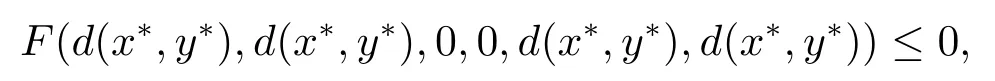
與F滿足條件(F2)矛盾.因此T有唯一的不動(dòng)點(diǎn)x*.

下證結(jié)論(c)成立.

由(2.2)可得

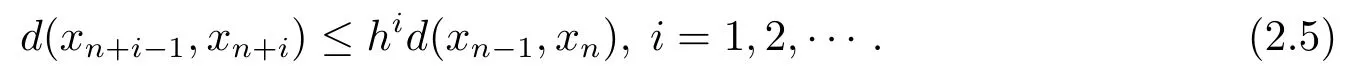
由(2.5)及三角不等式可得

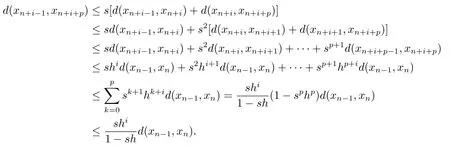
令p→∞時(shí)，可得結(jié)論(c)成立.

評(píng)注2.1當(dāng)s=1時(shí)，定理2.1為Berinde[5]在距離空間下建立的含有六元函數(shù)的隱性壓縮不動(dòng)點(diǎn)定理(文[5]中定理3.3)，因此是Berinde結(jié)果的推廣.

2018年，Karapinar等人[11]在距離空間中給出了另一類新的壓縮形式的定義，并證明了相關(guān)隱性壓縮不動(dòng)點(diǎn)定理.2019年，Aydi等人[12]在四角距離空間下建立了該類隱性壓縮不動(dòng)點(diǎn)定理.之后許多學(xué)者在不同空間下建立該類型的隱性壓縮不動(dòng)點(diǎn)定理.下面我們將Karapinar等人和Aydi等人的結(jié)果建立到b-距離空間.

定理2.2設(shè)(X，d)是系數(shù)為s的完備b-距離空間，T是X→X的自映射滿足，存在六元實(shí)值連續(xù)函數(shù)F:R+滿足條件(F1)，使得對任意x，y∈XFix{T}，有若d連續(xù)或者T連續(xù)時(shí)，則

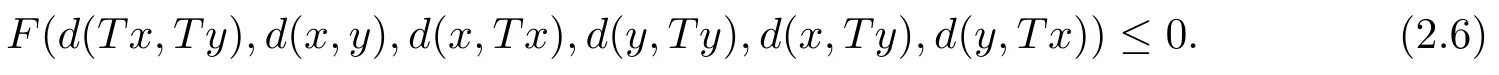
(a)T在X中有不動(dòng)點(diǎn)x*;

(b)由xn+1=Txn，n=0，1，···定義的迭代點(diǎn)列收斂于x*;

(c)當(dāng)sh＜1時(shí)，有以下估計(jì)成立

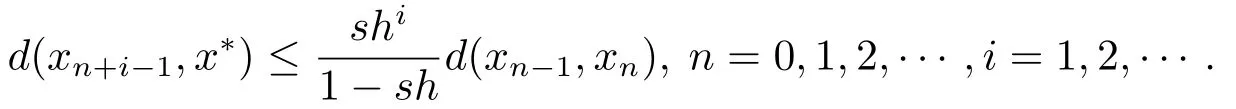
證任取x0∈XFix{T}，令xn+1=Txn=Tnx0，n=0，1，2，···，由此構(gòu)造迭代點(diǎn)列{xn}.不妨假設(shè)xnFix{T}，n=1，2，3···.

類似于定理2.1的第一步，可以證明{xn}是Cauchy列.由于X是完備的，故存在x*∈X，使得xn→x*(n→∞).下面分兩種情況證明x*是T的不動(dòng)點(diǎn).

情況1當(dāng)d連續(xù)時(shí).

反證法，假設(shè)x*Tx*，則x*∈XFix{T}.由(2.6)可得

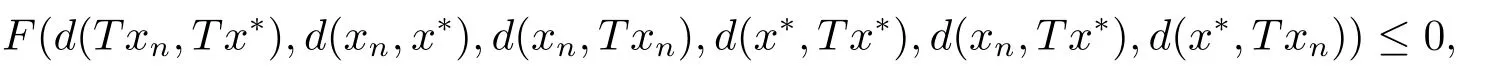
即

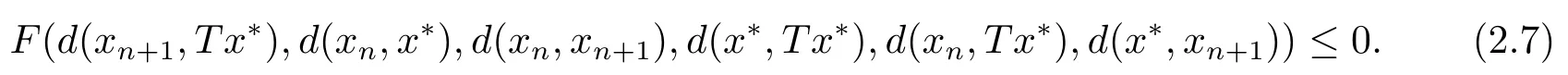
對(2.7)兩邊同時(shí)取極限，且由F滿足條件(F1)可得，

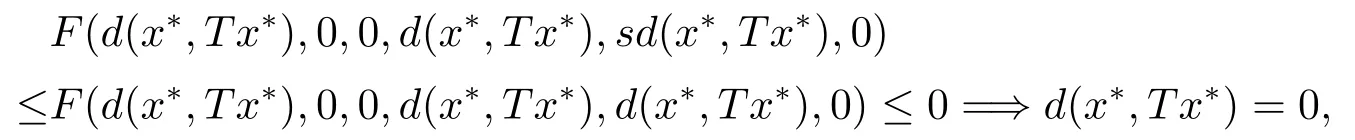
則與x*Tx*產(chǎn)生矛盾.因此x*是T不動(dòng)點(diǎn).

情況2當(dāng)T連續(xù)時(shí).

由T連續(xù)可得，

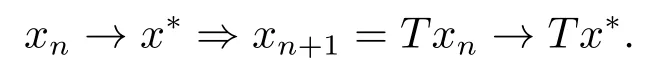
由于極限的唯一性，故x*=Tx*是T的不動(dòng)點(diǎn).

結(jié)論(b)，(c)的證明與定理2.1的證明相同，在此省略.

3.推論

這一部分我們將給出兩個(gè)主要定理的推論.

將定理2.1中的F取為例2.1中的1)可得下面的結(jié)果.

推論3.1設(shè)(X，d)是系數(shù)為s的完備b-距離空間，T是X→X的自映射.如果存在λ∈[0，1)滿足，對任意x，y∈X，有d(Tx，Ty)≤λd(x，y)，那么T在X中有唯一不動(dòng)點(diǎn).

評(píng)注3.1注意到推論3.1的條件d(Tx，Ty)≤λd(x，y)可以推出T是連續(xù)的.特別地，推論3.1就是文[14]中定理2.1，這個(gè)結(jié)果解決了Jovanovi′c等人[15]提出的公開問題.

將定理2.1中的F取為例2.1中的2)可得下面的結(jié)果.

推論3.2設(shè)(X，d)是系數(shù)為s的完備b-距離空間.設(shè)T是X→X的自映射滿足，存在λ∈對任意x，y∈X，有

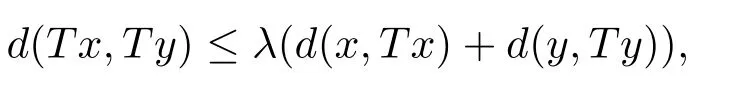
若d連續(xù)或者T連續(xù)時(shí)，則T在X中有唯一不動(dòng)點(diǎn).

評(píng)注3.2推論3.2是b-距離空間中的Kannan型壓縮不動(dòng)點(diǎn)定理，且壓縮條件與空間系數(shù)s無關(guān).

將定理2.1中的F取為例2.1中的3)可得下面的結(jié)果.

推論3.3設(shè)(X，d)是系數(shù)為s的完備b-距離空間.設(shè)T是X→X的自映射滿足，存在λ∈，對任意x，y∈X，有

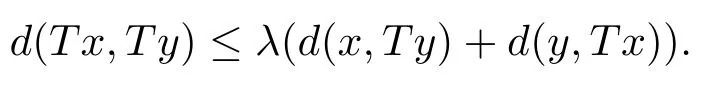
若d連續(xù)或者T連續(xù)時(shí)，則T在X中有唯一不動(dòng)點(diǎn).

評(píng)注3.3推論3.3是b-距離空間中的Chatterjea型壓縮不動(dòng)點(diǎn)定理.

將定理2.1中的F取為例2.1中的4)可得下面的結(jié)果.

推論3.4設(shè)(X，d)是系數(shù)為s的完備b-距離空間.設(shè)T是X→X的自映射滿足，存在λ∈對任意x，y∈X，有

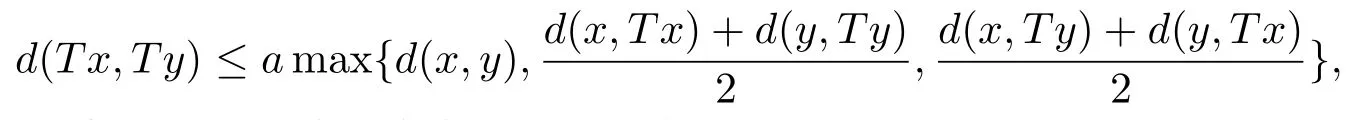
若d連續(xù)或者T連續(xù)時(shí)，則T在X中有唯一不動(dòng)點(diǎn).

將定理2.1中的F取為例2.1中的5)可得下面的結(jié)果.

推論3.5設(shè)(X，d)是系數(shù)為s的完備b-距離空間.設(shè)T是X→X的自映射滿足，存在λ1∈且對任意x，y∈X，有

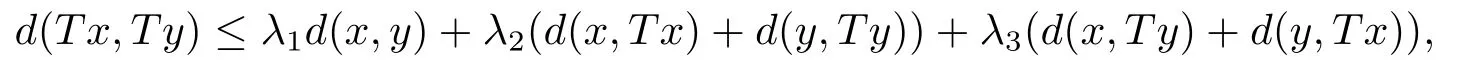
若d連續(xù)或者T連續(xù)時(shí)，則T在X中有唯一不動(dòng)點(diǎn).

將定理2.2中的F取為例2.3中的1)可得下面的結(jié)果.

推論3.6設(shè)(X，d)是系數(shù)為s的完備b-距離空間.設(shè)T是X→X的自映射滿足，對任意x，y∈XFix{T}，有

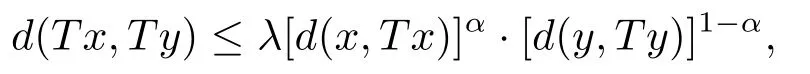
其中λ∈[0，1)，α∈(0，1).若d連續(xù)或者T連續(xù)時(shí)，則T在X中有不動(dòng)點(diǎn).

評(píng)注3.4推論3.6將Karapinar等人[11]提出的新的Kannan型壓縮不動(dòng)點(diǎn)定理建立到b-距離空間，這是Karapinar等人結(jié)果的推廣.

將定理2.2中的F取為例2.3中的2)可得下面的結(jié)果.

推論3.7設(shè)(X，d)是系數(shù)為s的完備b-距離空間.設(shè)T是X→X的自映射滿足，對任意的x，y∈XFix{T}，有

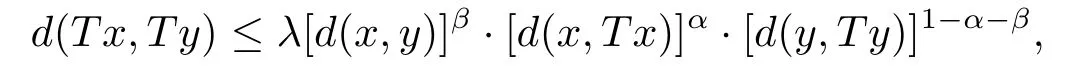
其中λ∈[0，1)，α，β＞0，且α+β＜1.若d連續(xù)或者T連續(xù)時(shí)，則T在X中有不動(dòng)點(diǎn).

評(píng)注3.5推論3.7將Aydi等人[12]提出的新的′Ciri′c-Reich-Rus型壓縮不動(dòng)點(diǎn)定理建立到b-距離空間.