擬齊次核的半離散Hilbert型不等式的最佳搭配參數

洪勇，陳強，吳春陽

(1.廣州華商學院應用數學系，廣東廣州511399;2.廣東第二師范學院計算機科學系，廣東廣州510303;3.廣東白云學院數學教研室，廣東廣州510450)

1.引言與預備知識

設r＞0，α∈R，分別定義序列空間與函數空間(0，+∞)為:

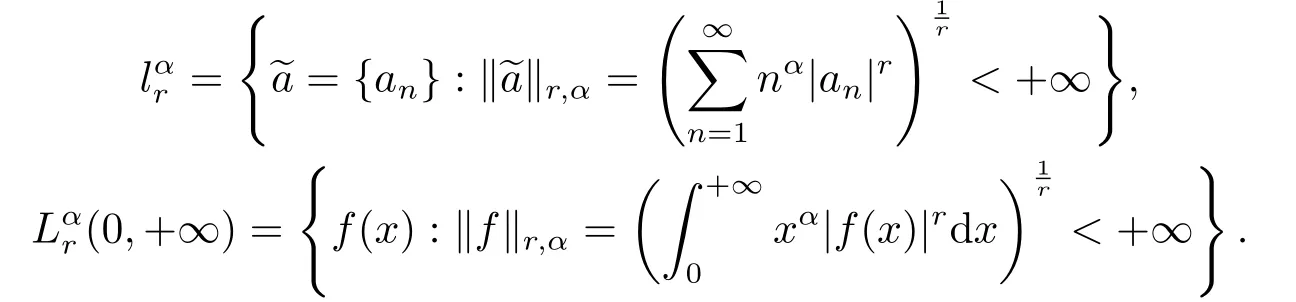
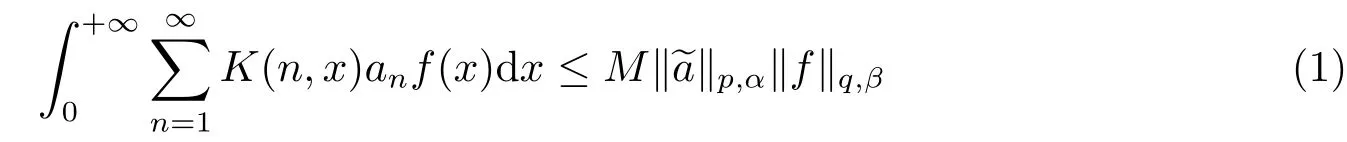
若分別定義級數算子T1與積分算子T2為：

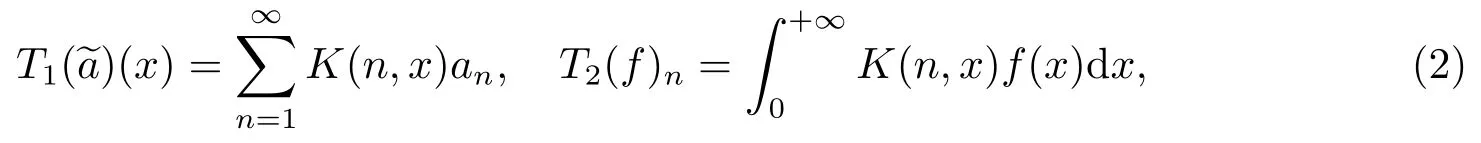
則T1可實現序列空間到函數空間的映射，T2可實現函數空間到序列空間的映射.根據Hilbert型不等式的基本理論，式(1)等價于

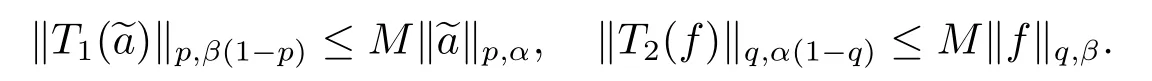
因此半離散Hilbert型不等式的研究對于討論T1與T2的有界性和算子范數具有重要意義.

設G(u，v)是λ階齊次函數，λ1λ2＞0，則稱K(n，x)=G(nλ1，xλ1)為擬齊次函數.顯然擬齊次函數K(n，x)具有性質:對?t＞0，有

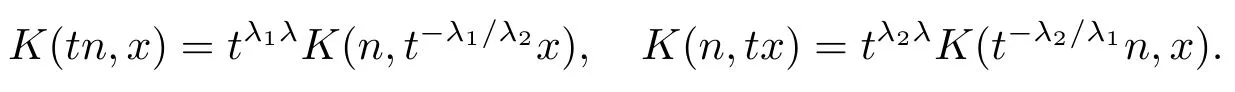
若選擇搭配參數a，b，根據Hlder不等式并利用權函數方法，可得下面形式的半離散Hilbert型不等式

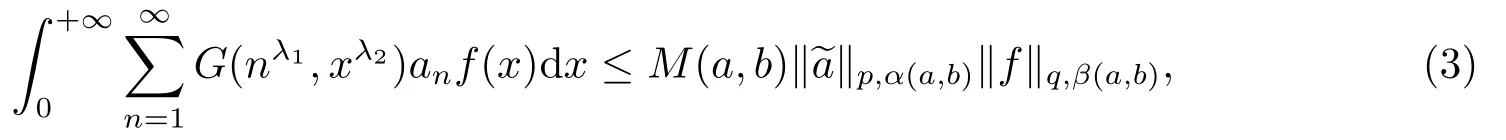
一般地，任意選取的搭配參數a，b并不能使式(3)的常數因子M(a，b)最佳.只有選擇特定的a，b，才能使M(a，b)是最佳值.目前，在國內外期刊中，許多的文獻通過選取最佳的搭配參數，已獲得了若干具有最佳常數因子的Hilbert型不等式.[1－10]本文對擬齊次核的半離散Hilbert型不等式，研究最佳搭配參數的充分必要條件，并討論其在算子理論中的應用.

引理1設G(u，v)是λ階齊次非負函數，設=1(p＞1)，a，b∈R，λ1λ2＞0，K(n，x)=+λ，K(t，1)t－aq在(0，+∞)上遞減，記

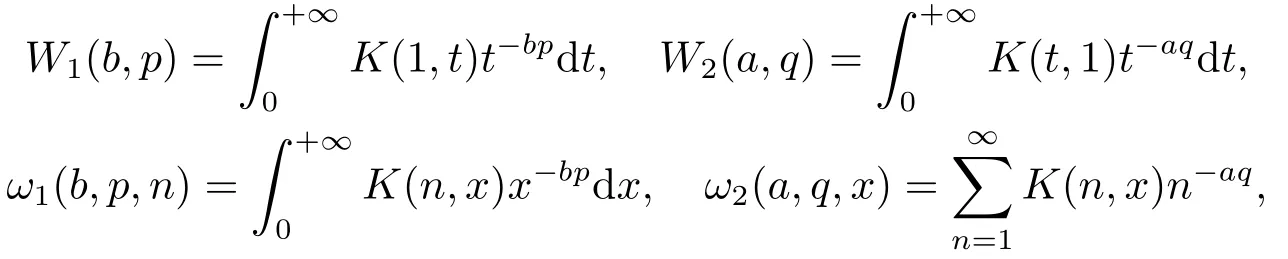
則λ1W2(a，q)=λ2W1(b，p)，且

證由擬其次函數的性質，并根據有

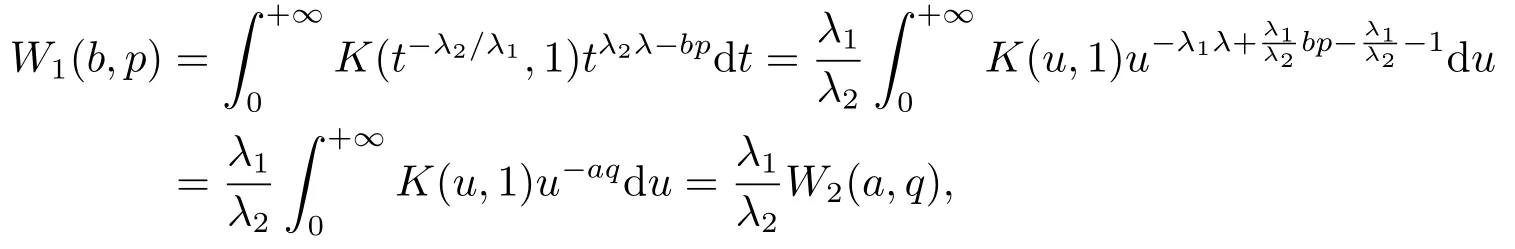
故λ1W2(a，q)=λ2W1(b，p).

根據K(t，1)t－aq在(0，+∞)上遞減，有

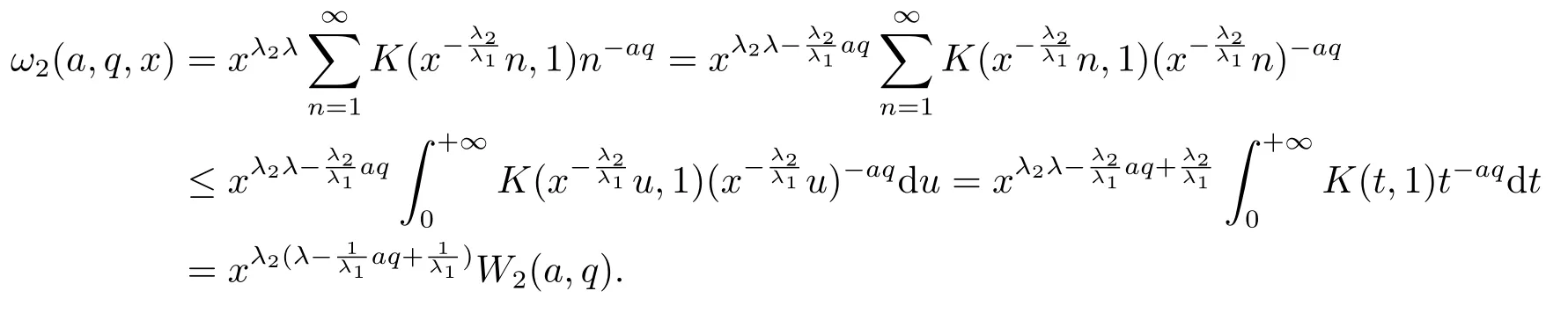
類似可證

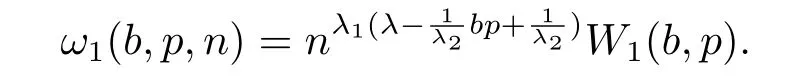
2.最佳搭配參數的充要條件

定理1設G(u，v)是λ階齊次非負可測函數，設=1(p＞1)，a，b∈R，λ1λ2＞0，K(n，x)=G(nλ1，xλ2)，=c，K(t，1)t－aq及K(t，1)t－aq+λ1c/p在(0，+∞)上遞減，且

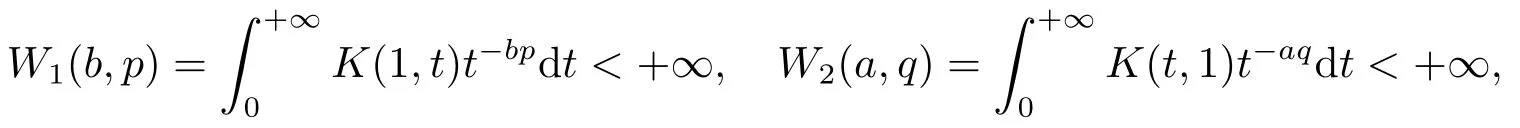
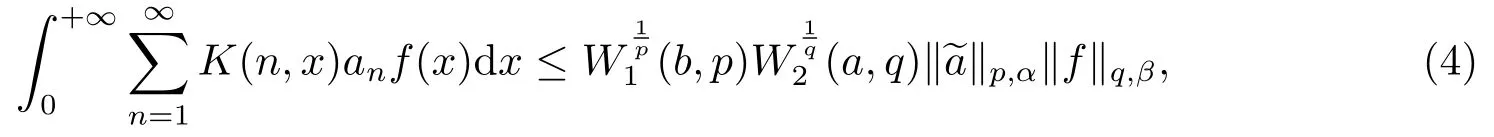
(ii)當且僅當c=0即+λ時，式(4)中的常數因子是最佳的.當c=0時，式(4)化為

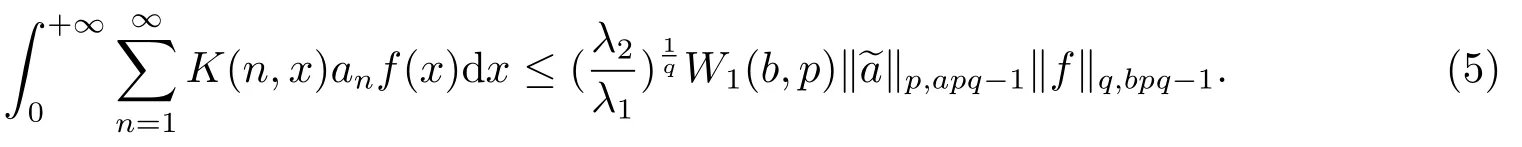
證(i)以a，b為搭配參數，根據混合型Hlder不等式和引理1，有

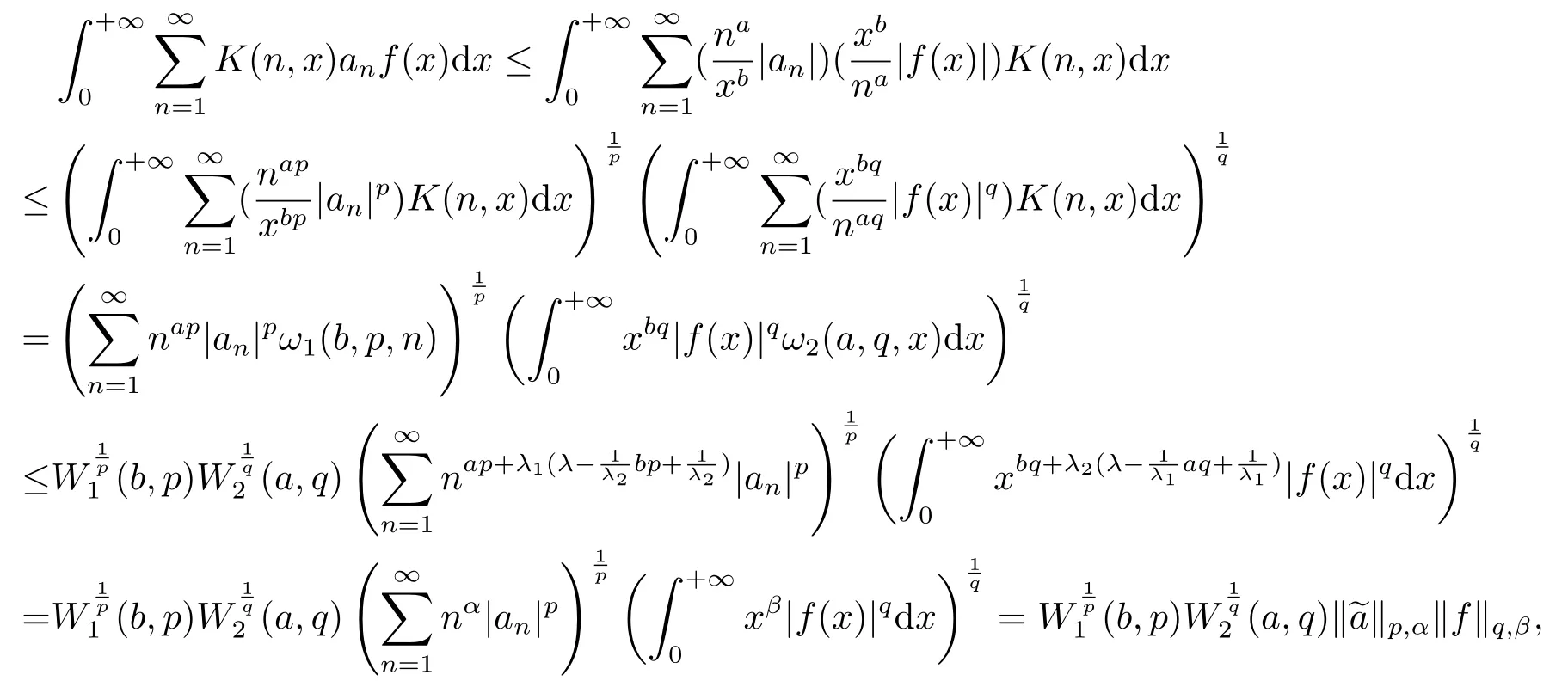
故式(4)成立.

(ii)充分性:設c=0.由引理1，有λ1W2(a，q)=λ2W1(b，p)，從而同時由c=0還可得α=apq-1，β=bpq-1，故式(4)可化為式(5).

若式(5)的最佳常數因子為M0，則且

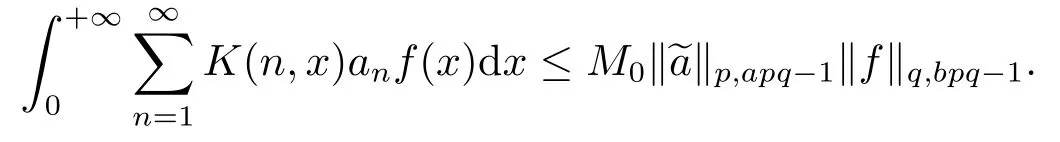
取充分小的ε＞0及足夠大的自然數N，令

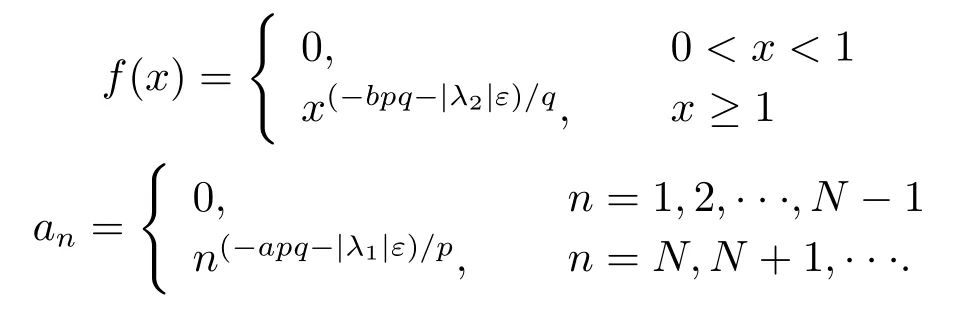
則可得

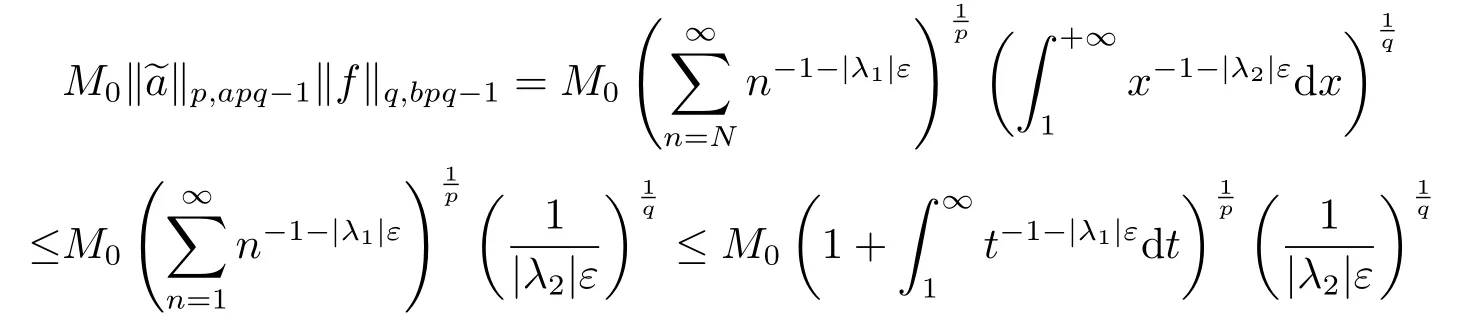
于是

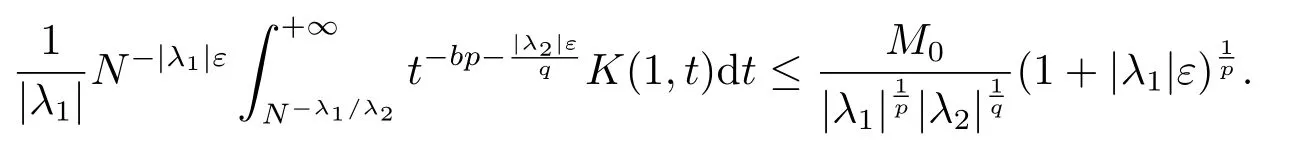
令ε→0+，得

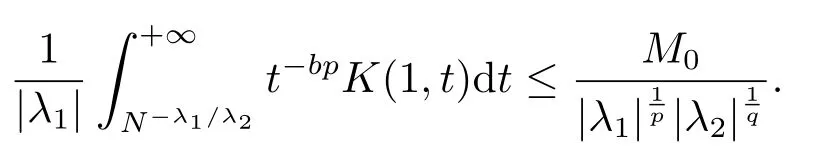
然后令N→+∞，得

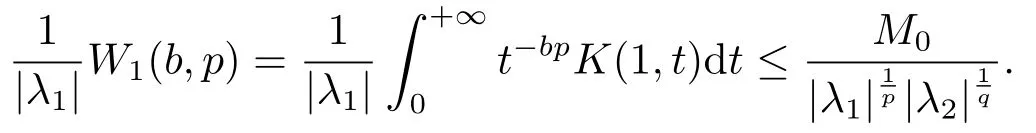
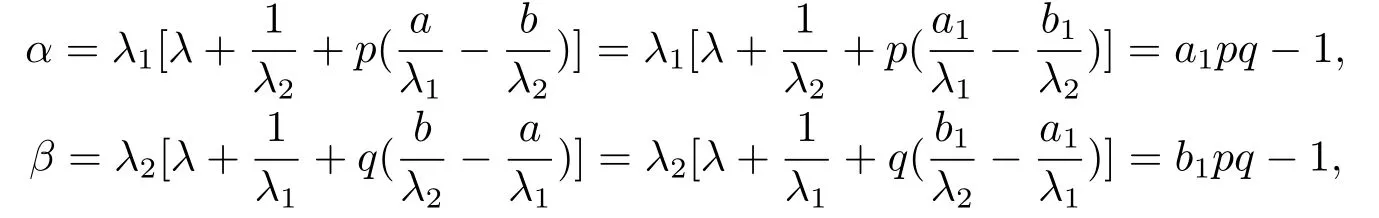
并經簡單計算可得

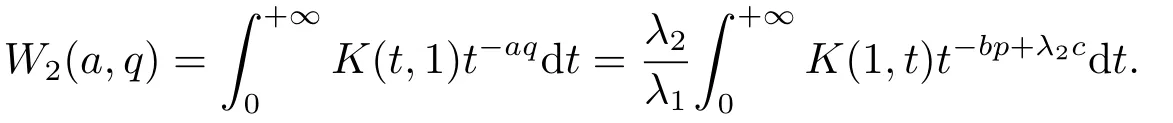
于是式(4)可等價地寫為

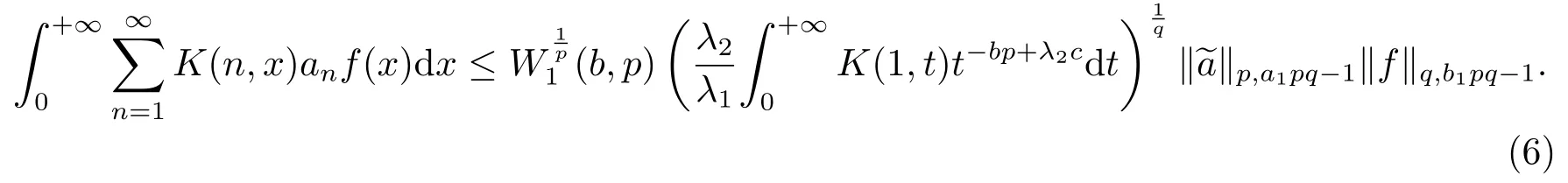
根據假設，式(6)的最佳常數因子是

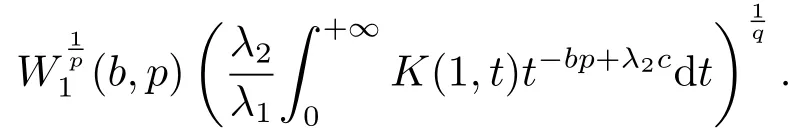
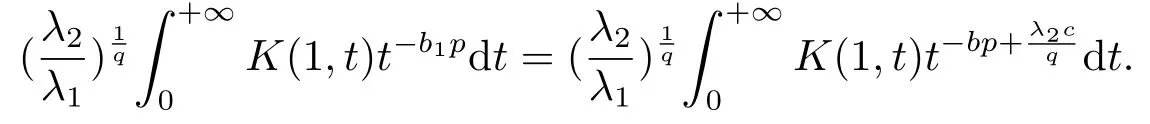
于是得到

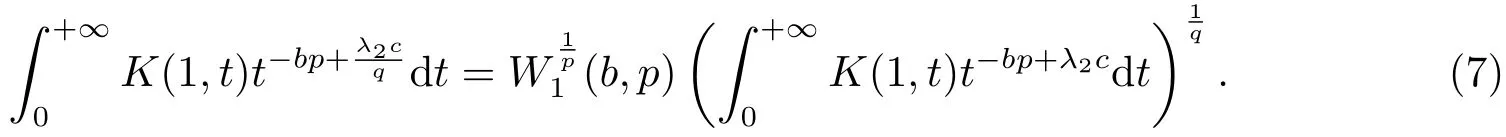
注記

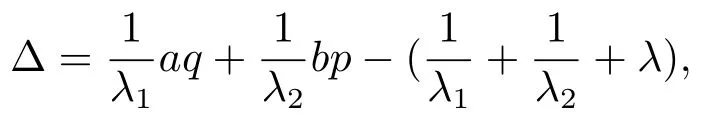
則式(4)中的常數因子最佳的充要條件是Δ=0.今后稱此Δ為判別式(4)常數因子最佳的判別式.

若K(n，x)=G1(nλ1/xλ2)，因G1(u/v)是0階齊次函數，于是由定理1可得下列推論1.

推論1設a，b∈R，λ1λ2＞0，K(n，x)=G1(nλ1/xλ2)非負可測，

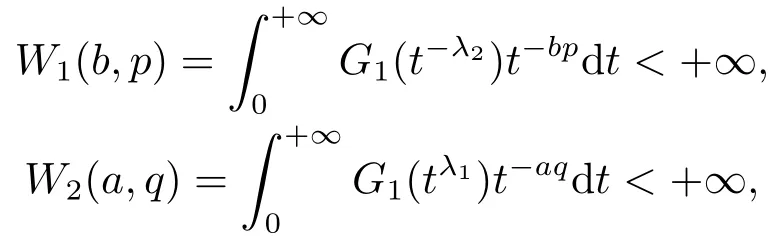
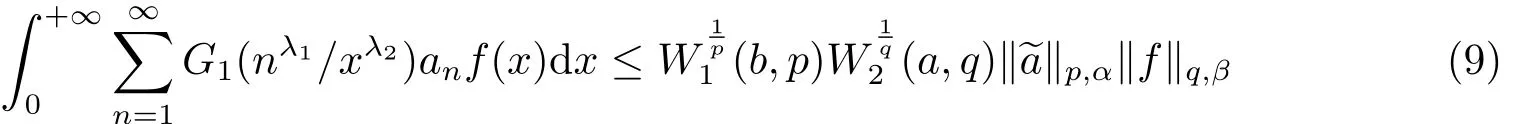
(ii)當且僅當c=0即時，式(9)中的常數因子是最佳的.當c=0時，式(9)化為

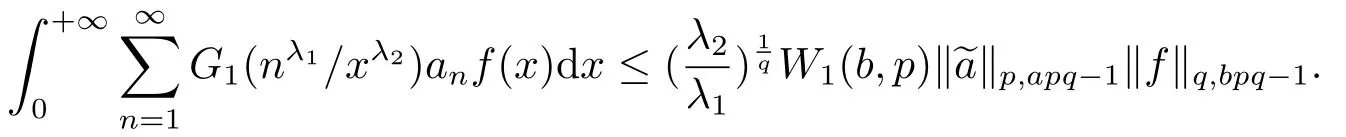
3.應用

根據半離散Hilbert型不等式(1)與式(2)定義的算子T1與T2的關系，由定理1可得下列定理2.

定理2設G(u，v)是λ階齊次非負可測函數，=1(p＞1)，a，b∈R，λ1λ2＞0，K(n，x)=G(nλ1，xλ2)，K(t，1)t－aq在(0，+∞)上遞減，α=apq-1，β=bpq-1，算子T1與T2如式(2)所定義，且

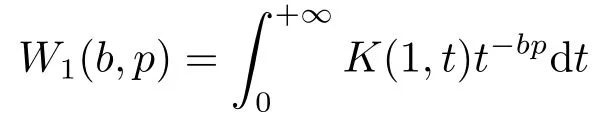
汽輪機排出的乏汽以直接空冷系統為主要冷卻方式，在此基礎上配置改進型海勒式間接空冷系統，從主排汽管道抽取部分乏汽送入DICSSAC，如圖1所示。DICSSAC作為輔助降低背壓的一種優化措施，可提高機組真空度，使機組安全、經濟運行。蓄冷是指夜間低溫時段，干式空冷換熱器分出一半冷卻單元用來冷卻凝結蓄冷水箱里的循環冷卻水。在第二天高溫時段，蓄冷水箱里的低溫循環冷卻水與流出干式冷卻塔的較高溫度循環水按一定比例混合，噴入噴射式凝汽器，進一步降低背壓[7]。

推論2設=1(p＞1)，λ1＞0，λ2＞0，a≥0，b≥0，a/b，α=且

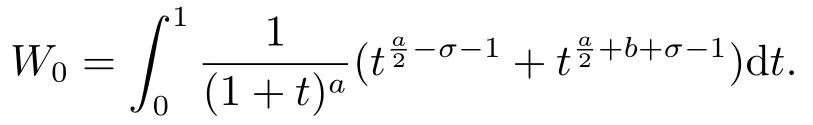
級數算子T1與積分算子T2分別為:

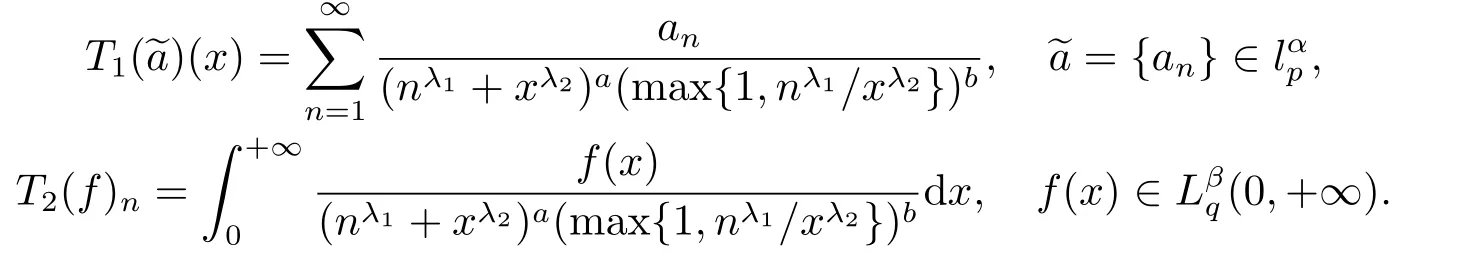
則T1:及都是有界算子，且T1與T2的算子范數為

證記

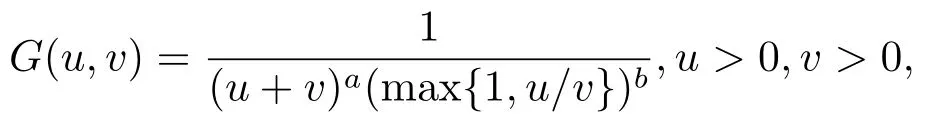
則G(u，v)是-a階齊次非負函數.

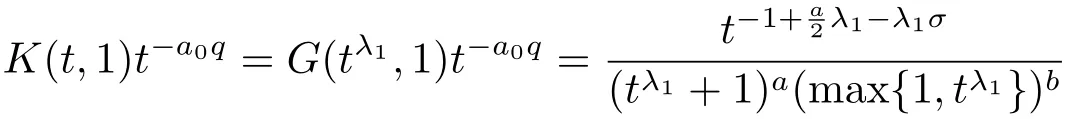
在(0+∞)上遞減.

在推論2中取b=0，可得推論3.

推論3設定義級數算子T1與積分算子T2分別為:

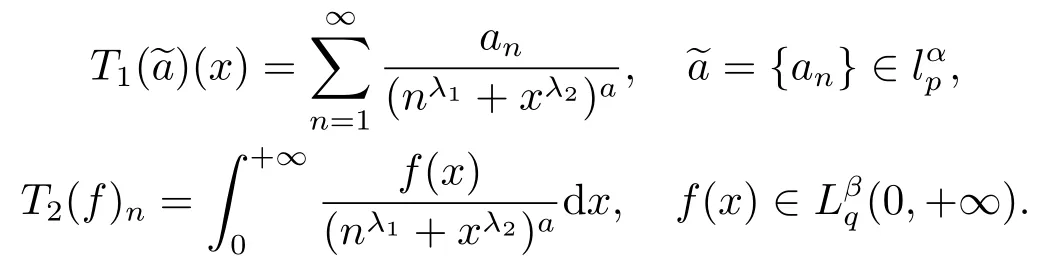
在推論2中取a=0，可得推論4.

推論4設=1(p＞1)，λ1＞0，λ2＞0，b＞0，max＜σ＜0，α=定義級數算子T1與積分算子T2分別為: