一類具有病毒變異的隨機(jī)SEIR傳染病模型的滅絕性與平穩(wěn)分布

杜金姬，秦闖亮，陳海波，李秋英

(1.信陽(yáng)學(xué)院數(shù)學(xué)與統(tǒng)計(jì)學(xué)院，河南信陽(yáng)464000;2.中南大學(xué)數(shù)學(xué)與統(tǒng)計(jì)學(xué)院，湖南長(zhǎng)沙410075;3.黃淮學(xué)院數(shù)學(xué)與統(tǒng)計(jì)學(xué)院，河南駐馬店463000)

1.引言

人們一直在使用動(dòng)力學(xué)方法來(lái)研究傳染病的傳播，并預(yù)測(cè)每次抵達(dá)流行病的趨勢(shì)[1－5].如果在傳染病的傳播過(guò)程中出現(xiàn)突變，很容易導(dǎo)致疾病失控.例如禽流感病毒(H7N9)、乙型肝炎及其他疾病.因此，研究遺傳變異病毒的過(guò)程有助于了解疾病和控制疾病的傳播.最近，文[6]中研究了一類具有病毒變異的SEIR傳染病模型的動(dòng)力學(xué)行為.另外，實(shí)際生活中任何事物都受到環(huán)境波動(dòng)的影響.因此，研究環(huán)境噪音對(duì)于疾病的影響是十分必要的[7－9].本文在文[6]模型的基礎(chǔ)上加入隨機(jī)擾動(dòng)，提出隨機(jī)SEIR傳染病模型:

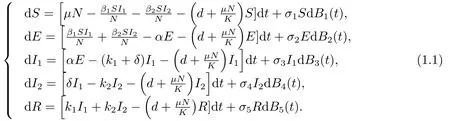
模型(1.1)中，總?cè)丝贜被分成了五部分S，E，I1，I2，R且N=S+E+I1+I2+R.S，E，I1，I2，R分別表示t時(shí)刻易感者，潛伏者，病毒變異前的感染者，病毒變異后的感染者，康復(fù)者，μ為總?cè)丝诔錾剩琩表示自然死亡率，β1為病毒變異前感染個(gè)體的感染率，β2為病毒變異后感染個(gè)體的感染率，K表示環(huán)境容納量，δ為病毒變異前的感染者變成病毒變異后的感染者的比率，α表示是病毒變異前潛伏個(gè)體成為感染個(gè)體的系數(shù)，k1為病毒變異前感染者的恢復(fù)率，k2為病毒變異后感染者恢復(fù)率.參數(shù)μ，d，K，β1，β2是正常數(shù)，δ，α，k1，k2為非負(fù)常數(shù).Bi(t)(i=1，2，3，4，5)是定義在一個(gè)完備概率空間(Ω，F(xiàn)，{F}t≥0，P)上的標(biāo)準(zhǔn)布朗運(yùn)動(dòng)，{F}t≥0滿足非降和右連續(xù)，0(i=1，2，3，4，5)表示白噪音強(qiáng)度.

在模型(1.1)中，總?cè)丝贜(t)滿足

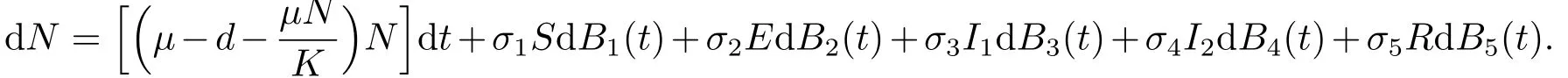
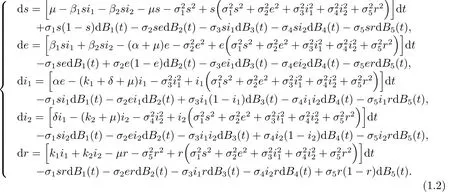
注意到變量s，e，i1，i2，r滿足關(guān)系r=1-s-e-i1-i2，我們可以忽略模型(1.2)的第五個(gè)方程探索簡(jiǎn)化模型

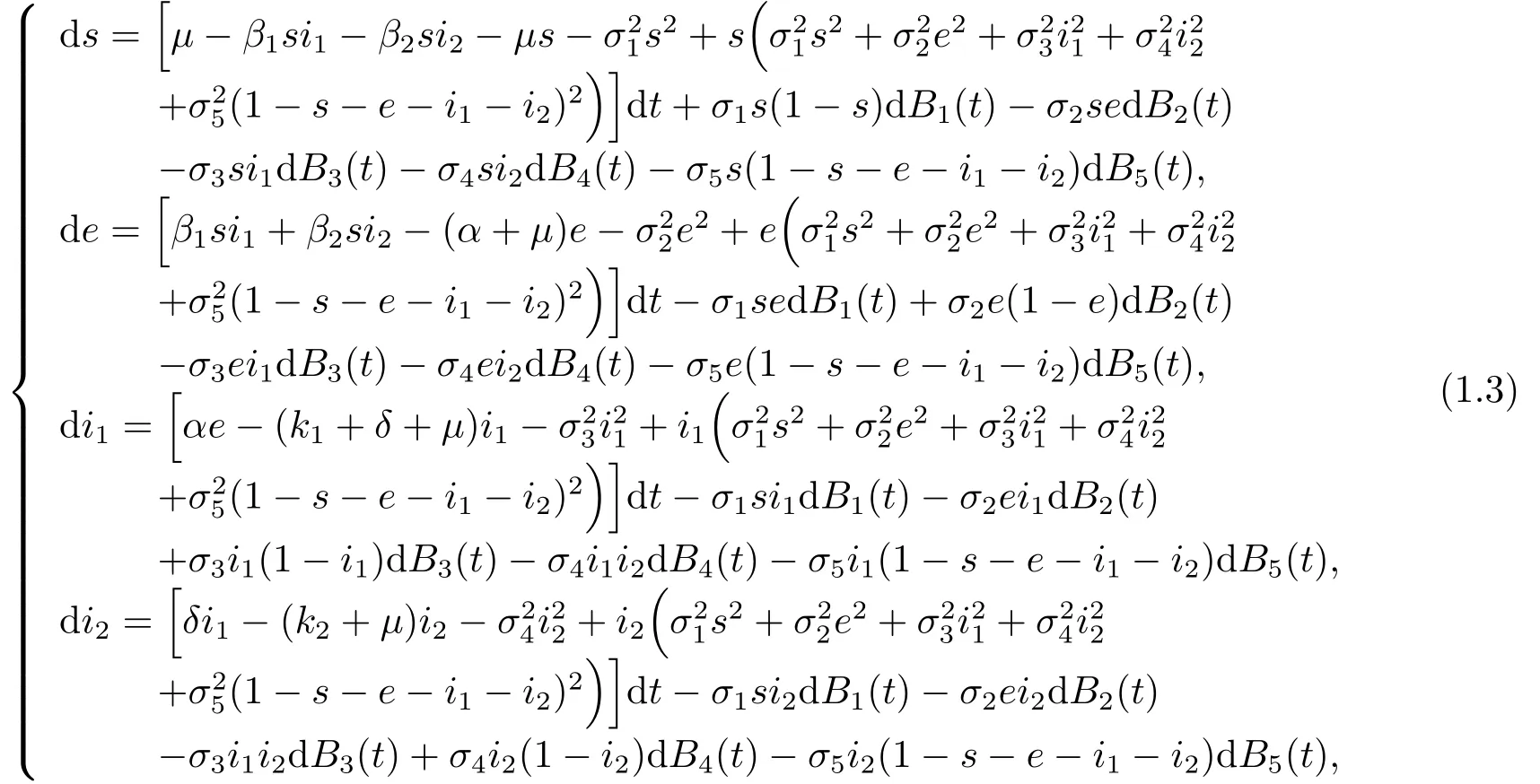
其中初始值(s(0)，e(0)，i1(0)，i2(0))∈且s(0)+e(0)+i1(0)+i2(0)＜1.

2.全局正解的存在唯一性

為了研究系統(tǒng)(1.3)的動(dòng)力學(xué)行為，我們首先證明系統(tǒng)存在全局正解.

定理2.1對(duì)于任意的初值(s(0)，e(0)，i1(0)，i2(0))∈且s(0)+e(0)+i1(0)+i2(0)＜1，當(dāng)t＞0時(shí)，模型(1.3)存在唯一正解(s(t)，e(t)，i1(t)，i2(t))并且以概率1位于內(nèi).

證因?yàn)槟Ｐ?1.3)的系數(shù)滿足局部Lipschitz條件，則對(duì)任意初值(s(0)，e(0)，i1(0)，i2(0))∈，存在一個(gè)t∈[0，τe)上的唯一局部正解(s(t)，e(t)，i1(t)，i2(t))∈，其中τe為停時(shí).為了證明解是全局的，我們僅需證明τe=∞a.s.為此，設(shè)k0＞0充分大，使s(0)，e(0)，i1(0)，i2(0)位于區(qū)間內(nèi).對(duì)每個(gè)整數(shù)k≥k0，定義停時(shí)

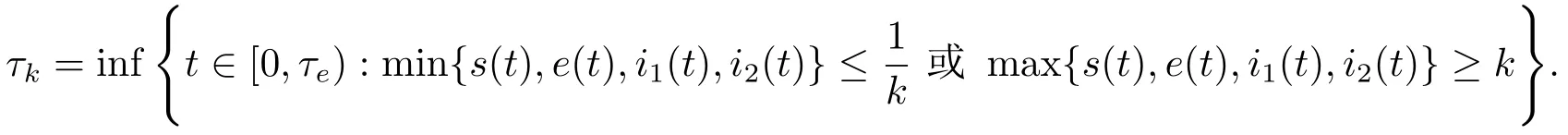
記inf?=∞(?表示空集).明顯地，τk隨著k→∞不斷增加.令因此τ∞≤τea.s.如果能證明τ∞=∞a.s.則τe=∞a.s.并且對(duì)所有的t≥0，(s(t)，e(t)，i1(t)，i2(t))∈a.s.也就是需要證明τ∞=∞a.s.如果不成立，那么存在一對(duì)常數(shù)T＞0和ε∈(0，1)使得P{τ∞≤T}≥ε.因此，存在一個(gè)數(shù)k1≥k0使得對(duì)所有的k≥k1，成立

定義一個(gè)C2-函數(shù)V:→R+如下：

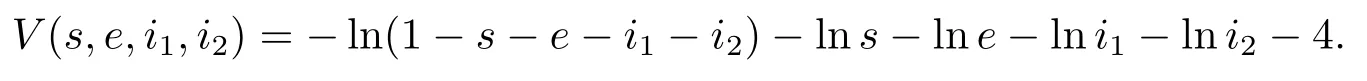
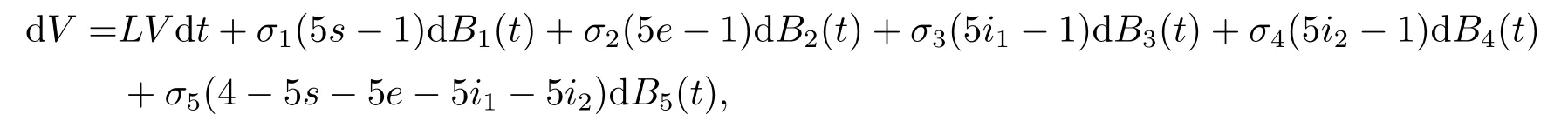
其中

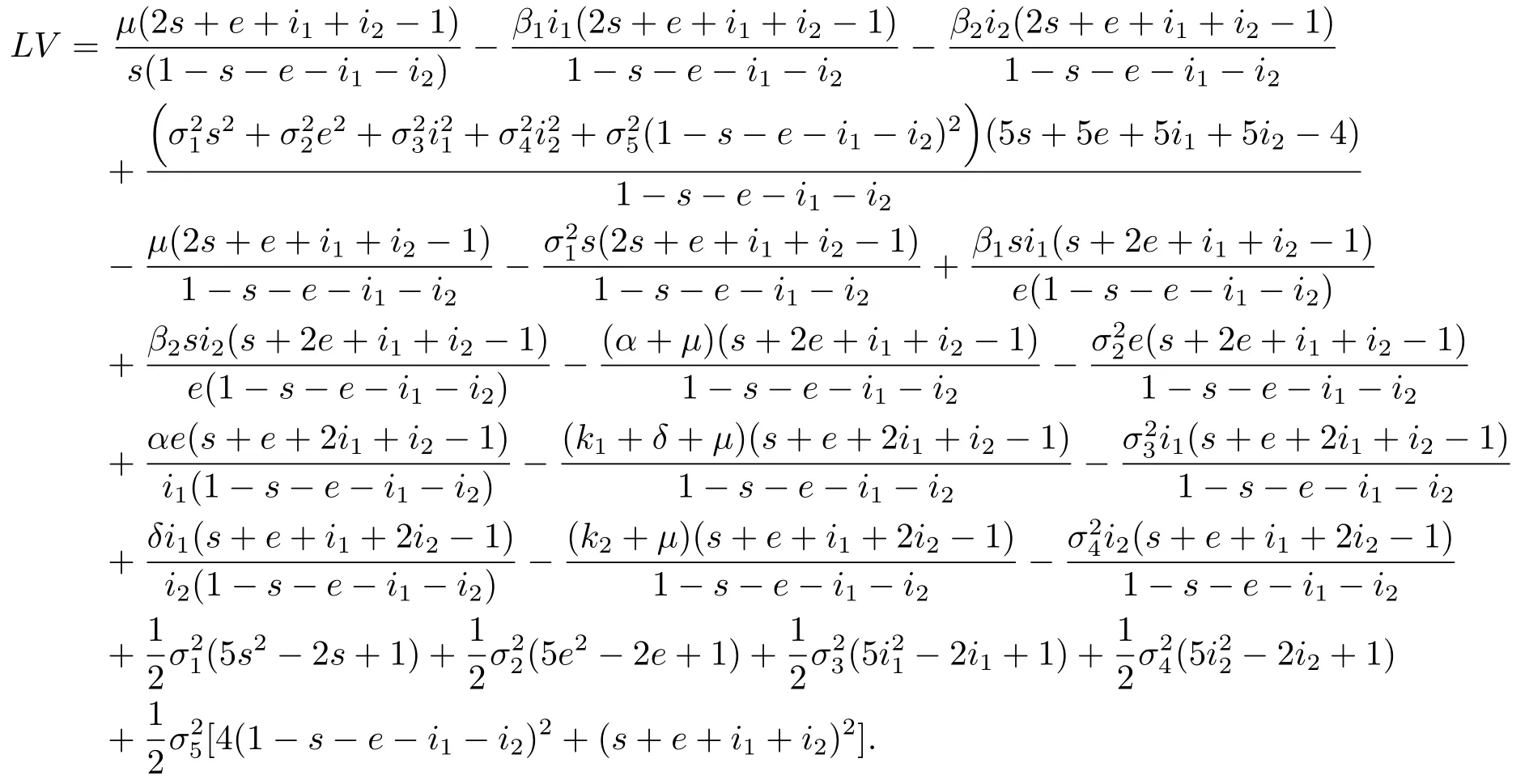
因?yàn)閞=1-s-e-i1-i2，所以

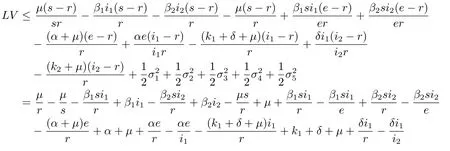
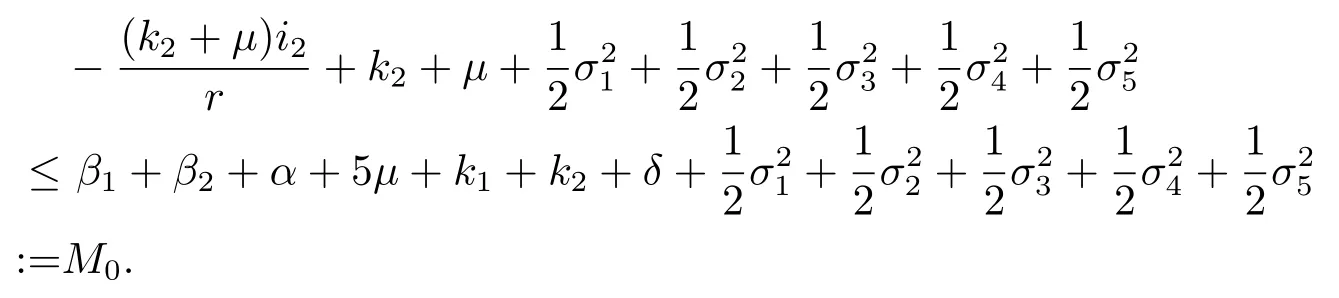
因此我們有

對(duì)(2.2)兩邊從0到τk∧T積分并取期望得

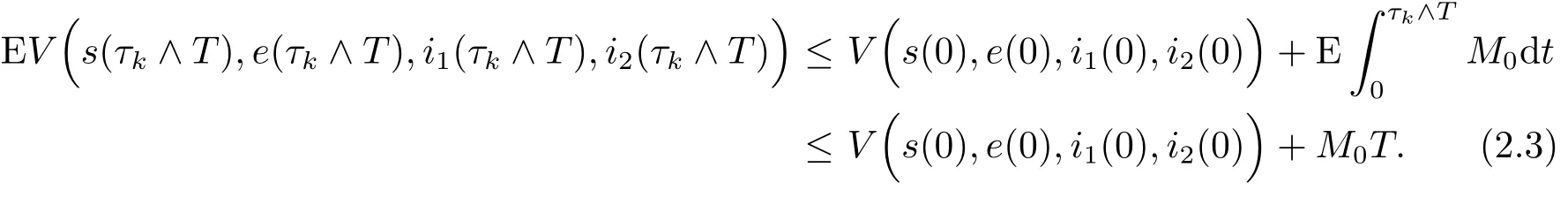
令Ωk={τk≤T}，k≥k1及由(2.1)式，有P(Ωk)≥ε.注意到對(duì)任意ω∈Ωk，都存在s(τk，ω)，e(τk，ω)，i1(τk，ω)，i2(τk，ω)等于或k.因此

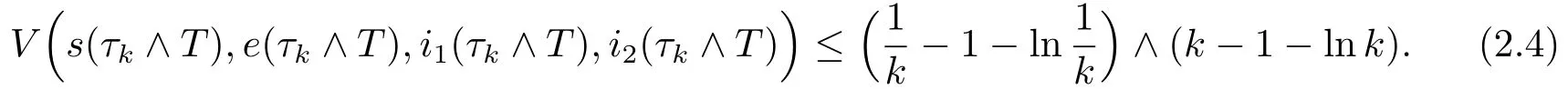
由(2.3)和(2.4)式，我們有

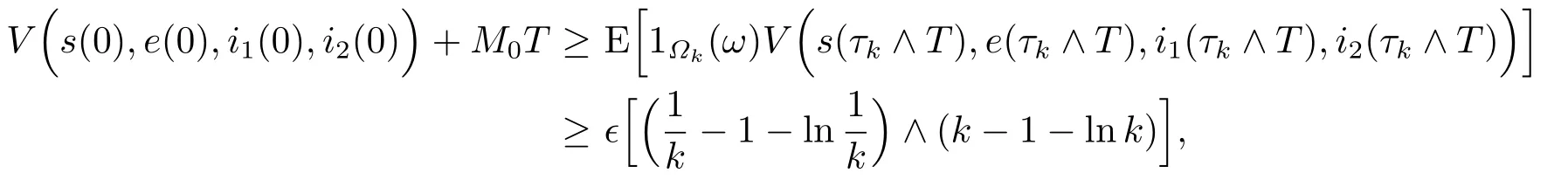
其中1Ωk(ω)是Ωk(ω)的特征函數(shù).

令k→∞，則有

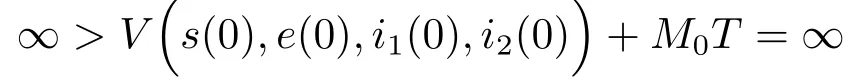
矛盾.顯然有τ∞=∞.定理得證.

3.疾病的滅絕性

本節(jié)我們討論系統(tǒng)(1.3)中疾病的滅絕性.

定理3.1對(duì)任意的初值(s(0)，e(0)，i1(0)，i2(0))∈且s(0)+e(0)+i1(0)+i2(0)＜1，若條件

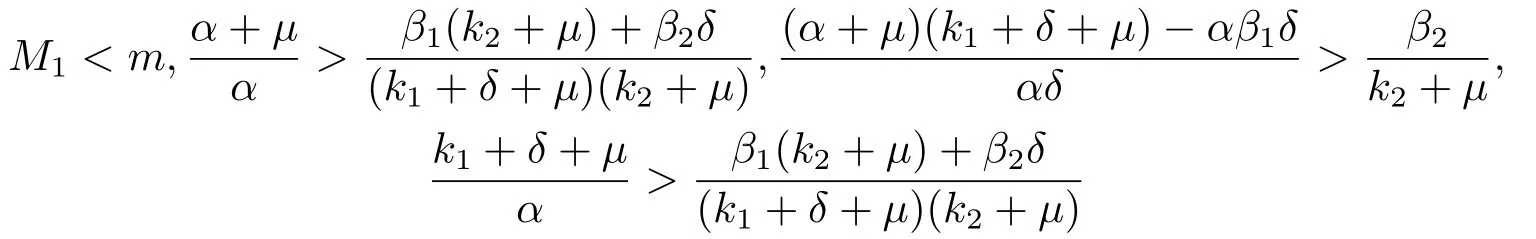
同時(shí)成立，則(e(t)，i1(t)，i2(t))指數(shù)收斂于(0，0，0)a.s.即疾病滅絕，其中

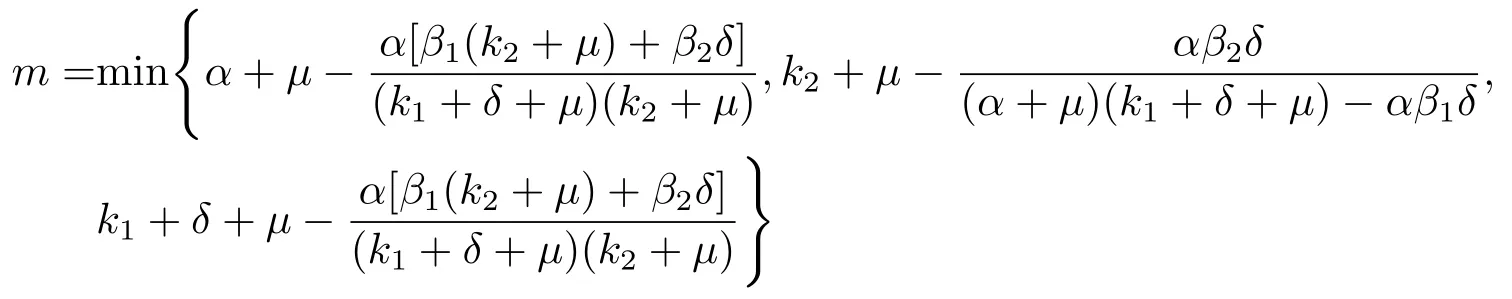
及

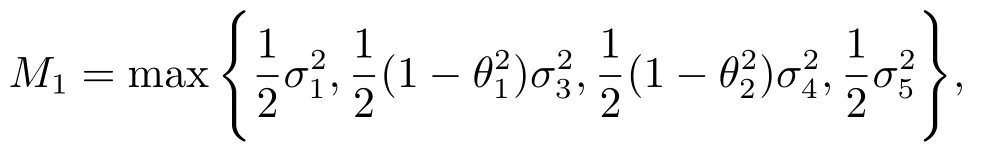
證定義一個(gè)可微函數(shù)V:

其中θ1，θ2是待定正數(shù).根據(jù)公式及模型(1.3)，得

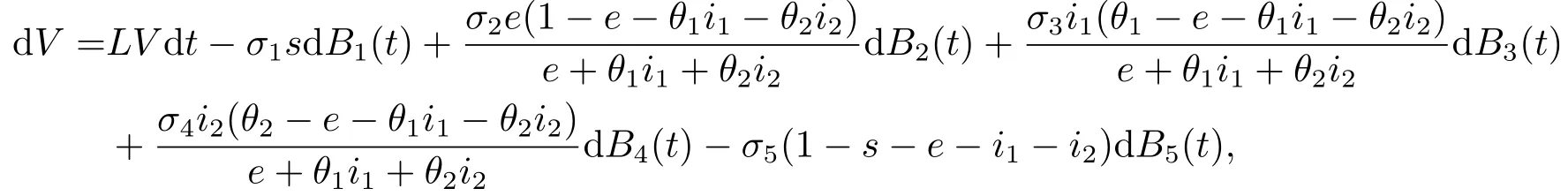
其中

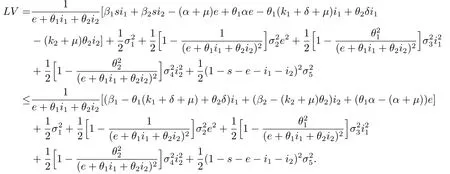
由(3.1)式，存在正數(shù)m使得

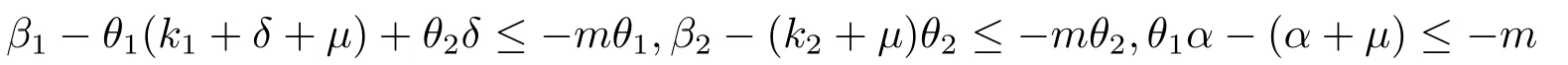
同時(shí)成立.因此有m＜k1+δ+μ，且及m＜α+μ，且及m＜k2+μ，且≤-m+k2+μ同時(shí)成立，則可取

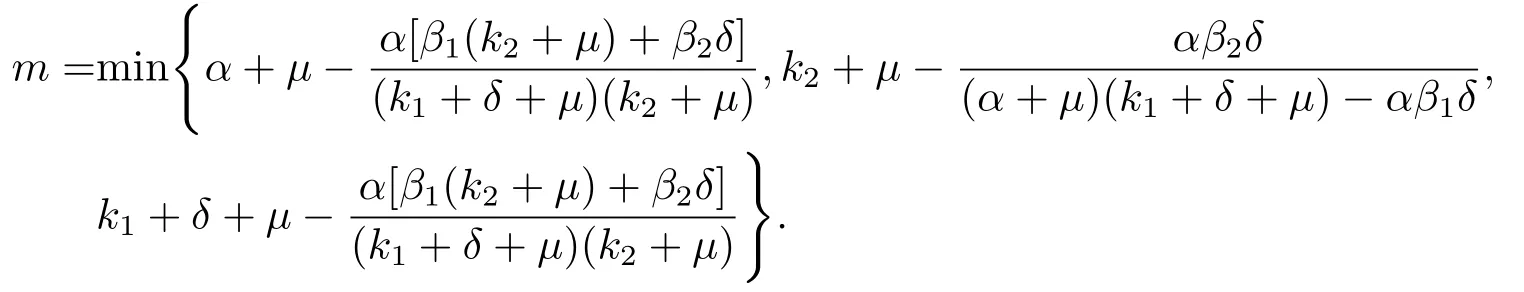
因此有

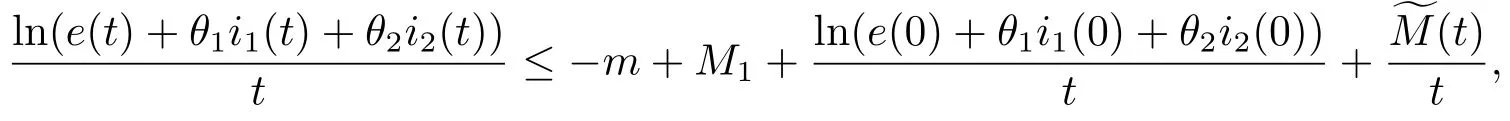
其中

由強(qiáng)大數(shù)定律得

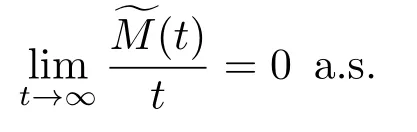
因此，

即

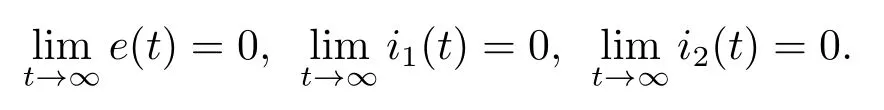
證畢.

4.平穩(wěn)分布及遍歷性

本節(jié)基于Khasminskii理論和Lyapunov函數(shù)法研究模型存在遍歷平穩(wěn)分布的條件，首先給出所需引理.

令X(t)是定義在d維Euclidean空間Ed上的齊Markov過(guò)程，并可有如下的隨機(jī)微分方程來(lái)描述：

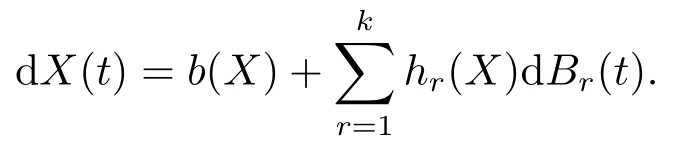
對(duì)應(yīng)的擴(kuò)散矩陣為

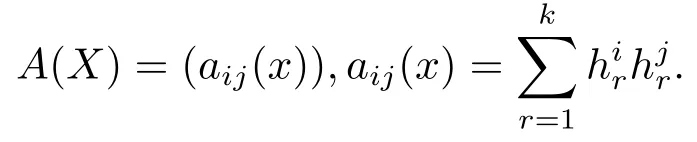
引理4.1[10]如果存在一個(gè)有規(guī)則邊界Γ的有界域D?Ed，并且：

(i)存在一個(gè)正數(shù)M，使得

(ii)存在一個(gè)非負(fù)C2函數(shù)V，使得LV對(duì)任意的x∈EdD是負(fù)的.則Markov過(guò)程X(t)存在唯一的遍歷平穩(wěn)分布π(·).

定理4.1設(shè)是系統(tǒng)(1.3)滿足初始條件及s(0)+e(0)+i1(0)+i2(0)＜1的解.若條件

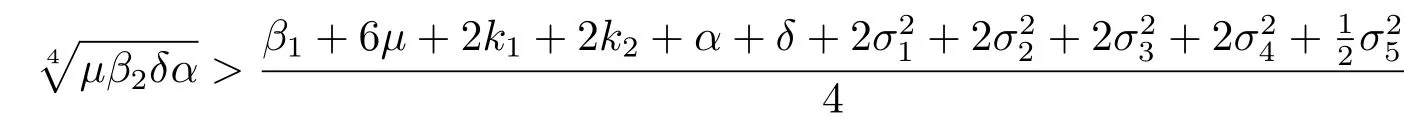
成立，則系統(tǒng)(1.3)存在唯一的遍歷平穩(wěn)分布π(·).

證定義正定函數(shù)V

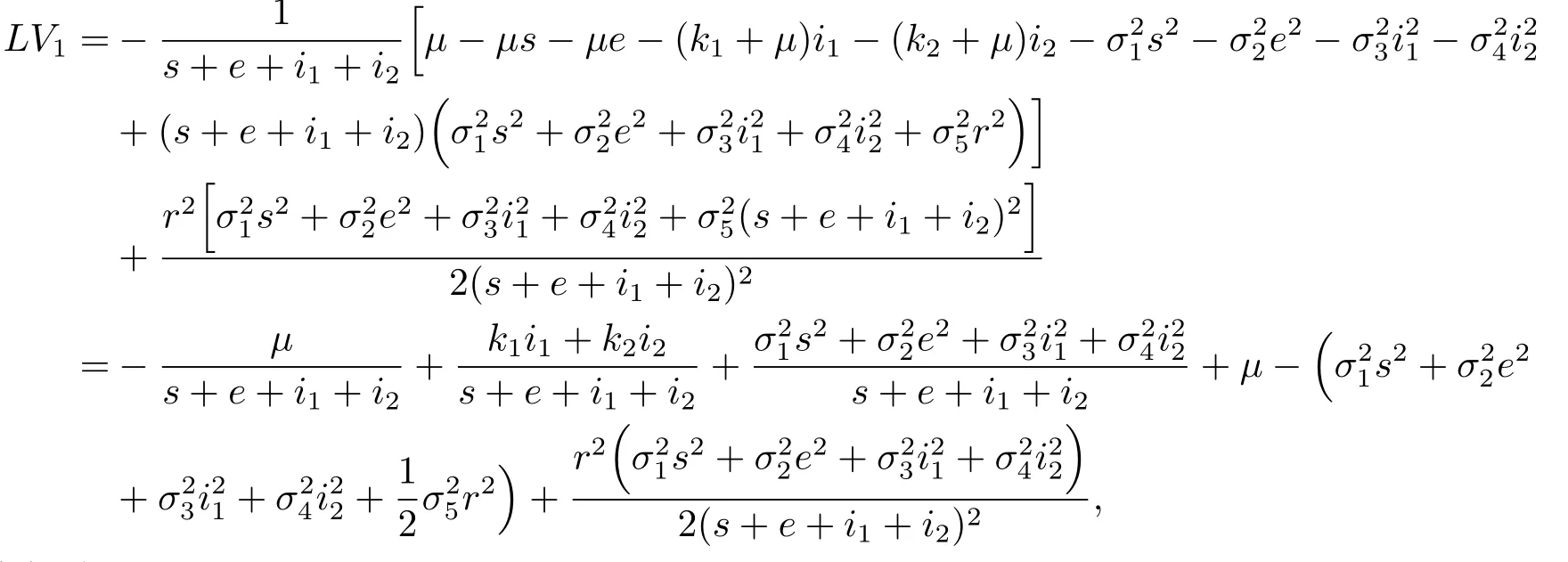
類似地，

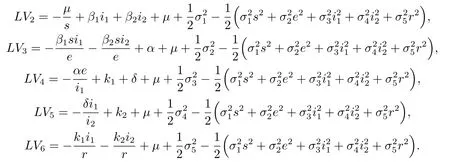
因此，

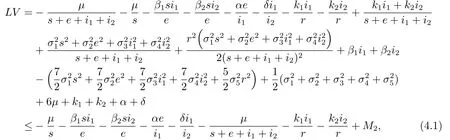
其中

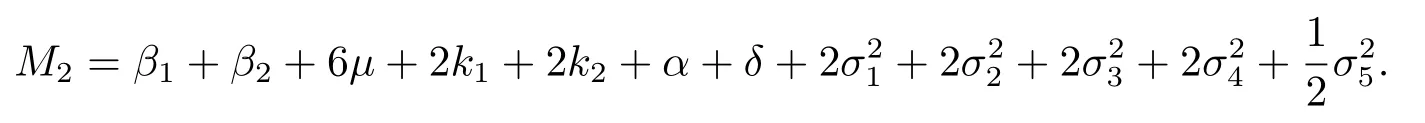
定義緊子集D:

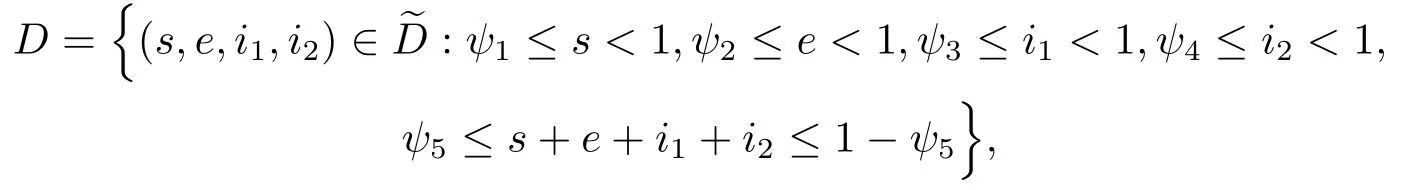
其中

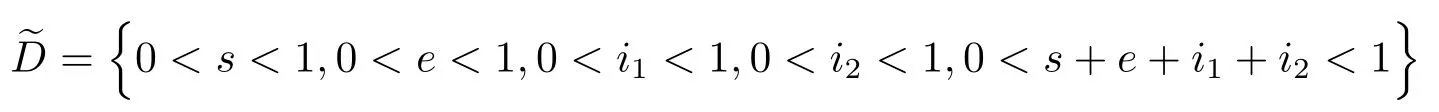
且ψi∈(0，1)足夠小滿足下列條件:

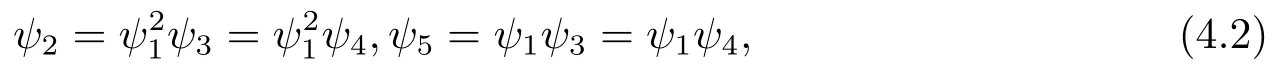
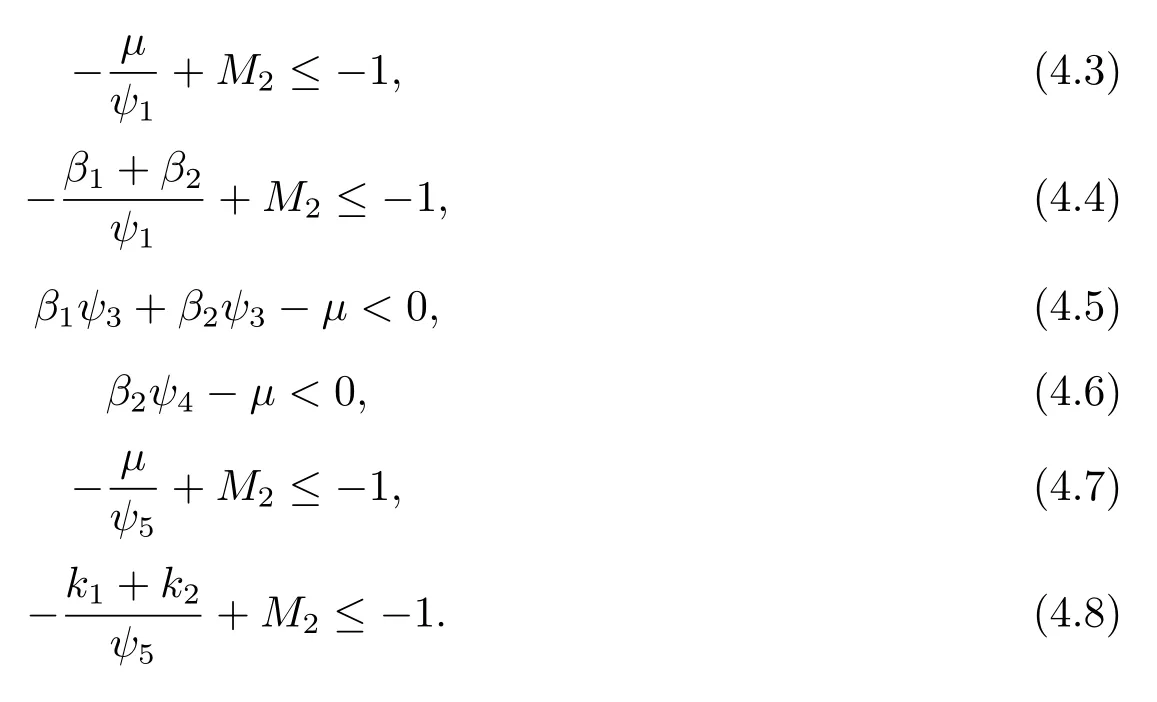
那么

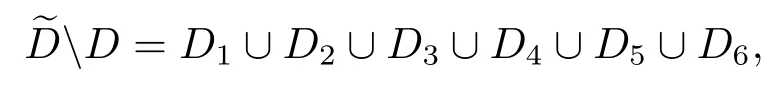
其中

下面我們證明LV恒負(fù).

情況1 如果(s，e，i1，i2)∈D1，由(4.1)及(4.3)得

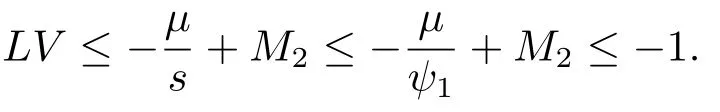
情況2 如果(s，e，i1，i2)∈D2，由(4.1)、(4.2)及(4.4)得

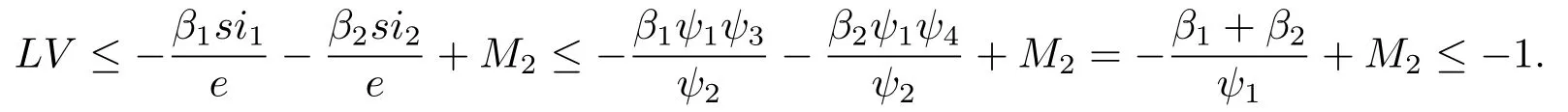
情況3 如果(s，e，i1，i2)∈D3，由(4.1)及(4.5)得

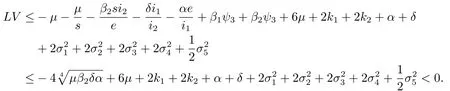
情況4 如果(s，e，i1，i2)∈D4，由(4.1)及(4.6)得

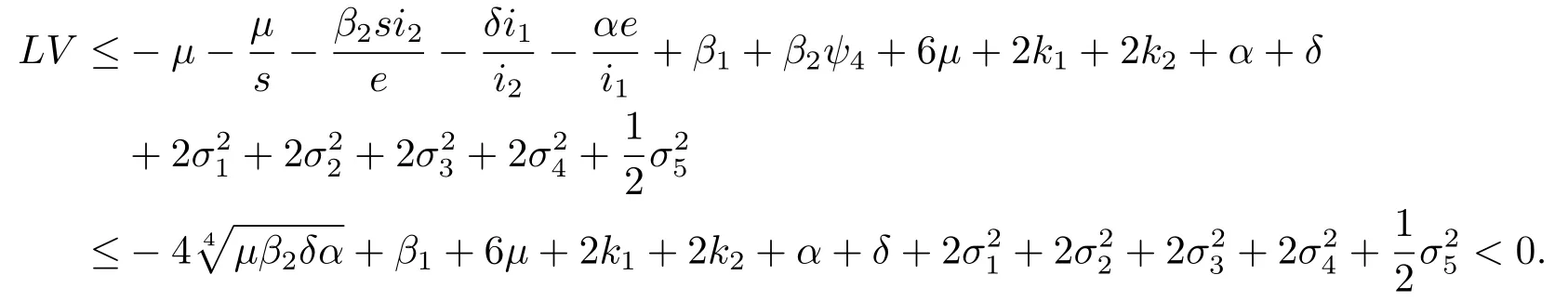
情況5 如果(s，e，i1，i2)∈D5，由(4.1)及(4.7)得

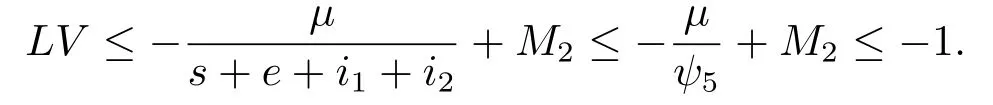
情況6 如果(s，e，i1，i2)∈D6，由(4.1)及(4.8)得

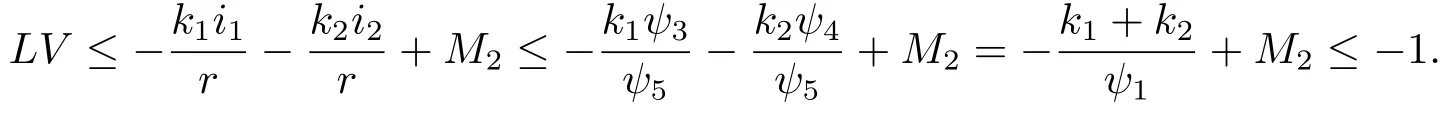
定義

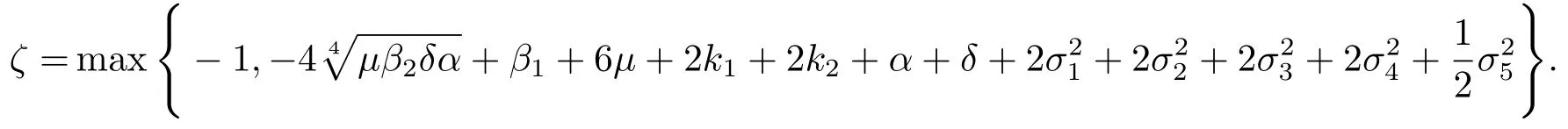
顯然對(duì)任意(s，e，i1，i2)∈D，有LV≤ζ＜0.另外，存在正數(shù)

使得

由引理4.1知，定理4.1結(jié)論成立.

5.數(shù)值模擬和結(jié)論

本節(jié)中我們通過(guò)數(shù)值模擬說(shuō)明結(jié)果的正確性.

圖5.1中取s(0)=0.35，e(0)=0.25，i1(0)=0.15，i2(0)=0.1，μ=0.1，β1=0.0005，β2=0.0016，k1=0.0666，k2=0.1428，δ=0.05，α=0.04，σ1=0.31，σ2=0.2，σ3=0.22，σ4=σ5=0.2，則M1=0.04805＜m≈0.2424，滿足定理3.1的條件，由定理的結(jié)論可知疾病將滅絕.

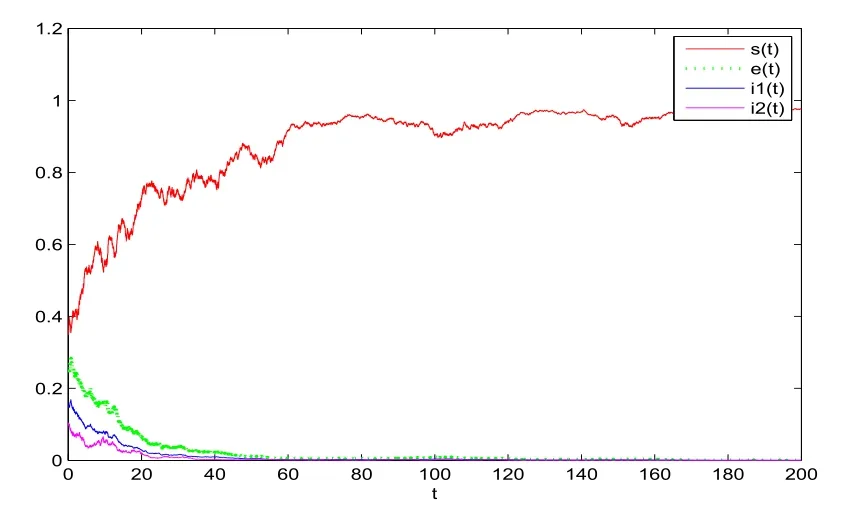
圖5.1 受感染個(gè)體滅絕的時(shí)間時(shí)序圖

圖5.2中取s(0)=0.45，e(0)=0.2，i1(0)=0.15，i2(0)=0.1，μ=0.01，β1=0.06，β2=1，k1=0.0222，k2=0.01428，δ=0.1，α=0.1，σ1=σ2=σ3=σ4=σ5=0.02，則滿足定理4.1的條件，則系統(tǒng)存在唯一的遍歷平穩(wěn)分布.

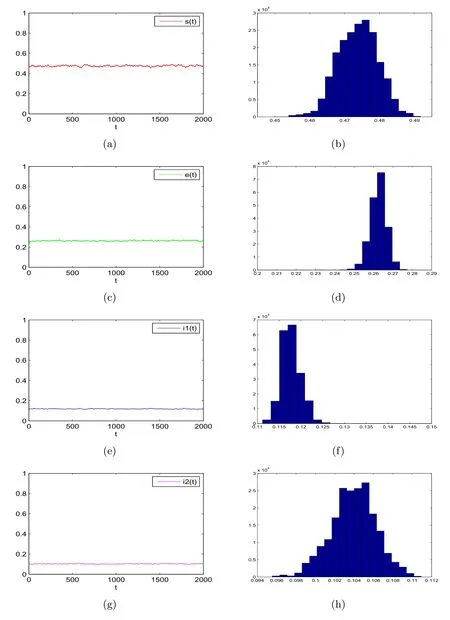
圖5.2 模型(1.3)的解s(t)，e(t)，i1(t)，i1(t)及其密度函數(shù)圖

本文應(yīng)用隨機(jī)分析的方法研究了一類高維隨機(jī)簡(jiǎn)化比例傳染病模型，得到疾病滅絕和系統(tǒng)正解存在唯一遍歷平穩(wěn)分布的充分條件，對(duì)模型的研究更加有利于控制疾病的傳播.