納米結構及浸潤性對液滴潤濕行為的影響*

李文 馬驍婧? 徐進良2) 王艷 雷俊鵬

1) (華北電力大學, 低品位能源多相流與傳熱北京市重點實驗室, 北京 102206)

2) (華北電力大學, 電站能量傳遞轉化與系統教育部重點實驗室, 北京 102206)

1 引 言

液滴在固體表面的潤濕行為是自然界中普遍存在的物理現象, 廣泛應用于印刷工藝、涂料技術、交通運輸、航空航天和能源系統等領域[1].眾所周知, 潤濕狀態(Cassie, Partial Wenzel和Wenzel)是影響冷凝液滴生長和脫離的關鍵因素[2,3].受自然界中“荷葉效應”[4-6]的啟發, 越來越多的學者關注超疏水表面的滴狀凝結換熱及強化機理.受液滴潤濕模式的影響, 超疏水納米結構表面冷凝存在彈跳、滾動和滑動三種液滴脫落模式[7], 研究液滴在納米結構表面的潤濕行為對減小液滴脫離尺寸, 促進冷凝液滴脫落, 進而強化滴狀冷凝傳熱有著重要意義.

目前研究的粗糙表面上的潤濕狀態主要分為Wenzel模型[8]和Cassie模型[9]兩種理論.Wenzel[8]認為粗糙表面的存在使得實際固-液接觸面積大于所觀察到的表面面積, 并假設液滴完全充滿納米結構并潤濕壁面.潤濕表面的表觀接觸角(θw)和本征接觸角(θe)之間滿足關系:

其中r為粗糙度因子, 表示液滴與固體表面接觸的實際面積與投影面積的比值.Cassie和Baxter[9]進一步拓展了Wenzel方程, 認為液滴在粗糙表面上的接觸是一種復合接觸, 當表面較疏水時, 液滴不能完全潤濕凹槽, 液滴與表面之間有空氣存在,所以表觀上的固-液接觸面實際上由固-液接觸面和氣-液接觸面共同組成.復合表面的表觀接觸角θc可以表示為其中f表示與液體接觸的實際固體表面占比, 稱為相面積分數.

液滴在固體表面的潤濕性主要取決于表面的化學組成[10-15]、微結構形貌[16-18]和幾何結構尺寸[15,19-21].He等[22]采用實驗方法研究了水滴在不同浸潤性和幾何參數的表面上的潤濕行為, 研究表明, 當水滴直接在固體基板沉積時形成接觸角較大的Cassie潤濕狀態, 當水滴以一定高度降落到表面時形成接觸角較小的Wenzel潤濕狀態.Bico等[23]討論了液滴在納米結構表面的潤濕行為及不同潤濕狀態轉換的可能性.結果發現增大柱高和柱寬、減小柱間距均有利于Cassie液滴的形成.Marmur[21]通過計算潤濕面積定量評價液滴在粗糙表面的潤濕行為.研究結果補充了Wenzel[8]和Cassie[9]理論.由于實驗技術條件和理論模型的限制, 當液滴的特征尺度為微納米級別時, 表面積與體積的比值明顯增大, 宏觀尺度下能夠忽略的某些影響因素(分子間的范德瓦耳斯力、液體流動出現的壁面滑移效應、傳熱過程出現的溫度階躍等)變得不容忽視.因此, 在微納尺度下, 物理現象所具有的尺度效應和界面效應逐漸成為探究潤濕和傳熱等宏觀尺度現象影響機理的重要因素.近年來,分子動力學(molecular dynamics, MD)模擬技術快速發展, 并被廣泛應用于探究納米尺度下分子間相互作用及機理.Shi和Dhir[24]討論了采用MD模擬得到的水滴在鉑表面潤濕的接觸角和氬液滴在鉑表面潤濕的接觸角, 與實驗中水滴在鋁表面潤濕的接觸角的關系, 發現上述三種接觸角隨體系溫度的變化規律一致, 均隨溫度的增加而降低.Li等[19]研究了氬液滴在固體鉑表面上的潤濕行為, 結果表明, 液滴的接觸角及總蒸發量隨表面浸潤性的增加而減小.Yong和Zhang[25]研究了改變柱高和相面積分數, 汞液滴在固體銅溝槽上的潤濕特性, 并將模擬結果與Wenzel[8]和Cassie[9]理論預測結果對比, 發現液滴在疏水表面潤濕的接觸角模擬值與理論計算值符合較好, 然而液滴在親水表面潤濕的接觸角模擬值較理論計算值偏大, 造成該現象的原因是納米尺度下親水表面高的邊緣密度使得釘扎效應明顯.Saha等[18]研究了水滴在不同幾何參數(柱高、柱寬、柱間距)的石墨表面上的潤濕特性,發現在最佳柱間距下, 相較水滴在方柱陣列表面上的潤濕, 水滴在圓柱陣列表面的潤濕具有更高的流動性.Chen等[15]研究了不同參數(柱高、柱間距和水滴尺寸)對Wenzel狀態向Cassie狀態自發轉換的影響.結果表明, 水滴在硅表面上潤濕狀態的轉換分為固-液接觸面積減小和水滴上升兩個階段.當柱高位于21.72—48.87 ?時, 上述潤濕轉換過程發生的概率隨液滴尺寸的減小和柱間距的增大而減小.

目前文獻對液滴潤濕行為的研究主要集中于欄柵形、方柱陣列等規則形狀的納米結構[15,20], 而低表面張力的流體容易滲入凹槽形成黏滯力較強的潤濕接觸, 導致液滴不易從表面脫離, 給超疏水表面的制備帶來困難, 因此增強能量勢壘實現復合接觸成為一個重大的挑戰.可重入結構(如“T”或蘑菇形狀及懸垂形結構等)逐漸成為研究者關注的焦點.Savoy和Escobedo[26]采用MD方法模擬了不同尺寸的液滴在“T”形結構上的潤濕行為, 發現潤濕與方柱相同高度的該結構表面需要克服更高的能量勢壘, 一定程度上增強了表面疏水性.Wang等[27]通過實驗方法研究了不同表面邊緣角和工質對液滴潤濕特性的影響, 結果表明, 尖銳的表面邊緣帶來的強釘扎作用, 可以顯著改變液滴在表面的接觸角和潤濕狀態.Zhu等[28]采用MD方法研究了不同參數(固體底角、表面浸潤性)對水滴潤濕狀態轉換的影響, 研究表明, Cassie態向Wenzel態轉換的臨界本征接觸角對固體底角有很強的依賴性, 而Wenzel態向Cassie態轉換的臨界本征接觸角與固體底角呈相反的規律, 并通過模擬宏觀降雨計算了潤濕轉換的自由能壘, 定量評估Cassie狀態的穩定性.本文提出了三種不同形貌(縱截面分別為倒梯形、長方形和正梯形)的納米結構表面,采用MD方法研究納米結構傾角(60°, 90°和120°)及表面浸潤性對液滴潤濕行為的影響, 為提高Cassie狀態的穩定性、制備親水材料的超疏水表面和強化滴狀凝結換熱提供一定指導意義.本模擬采用開源MD模擬軟件LAMMPS實現, 原子位型可視化采用OVTTO軟件.

2 模型建立及模擬細節

2.1 模型構建

本文采用MD方法研究了納米液滴在不同粗糙表面的潤濕行為.圖1(a)為初始狀態的MD模型.模擬體系的大小為Lx×Ly×Lz= 19.58 nm ×19.58 nm × 17.62 nm,x和y方向采用周期性邊界條件,z方向采用固定邊界條件.整個體系溫度恒定為100 K (本文計算側重于亞臨界壓力下的氣-液相平衡, 該溫度低于氬的臨界溫度150.7 K,100 K對應的飽和壓力為0.32377 MPa, 同樣低于氬的臨界壓力4.863 MPa).圖1(b)為物理模型的俯視圖, 其中紅、黃色原子代表固體壁面的Pt原子, 固體基板厚度δ為3σ, 共6層原子.按照面心立方晶格結構排布, 密度為21.45 × 103kg/m3, 晶格常數為1.15σ, 其(111)晶面與液體原子接觸.納米結構形狀如圖1(c)所示, 對應三種傾角φ(60°,90°和120°), 固體原子數為28806—43958個.藍色原子代表液滴原子Ar, 因為Ar屬于單原子分子,氬原子間的Lennard-Jones (LG) 勢函數具有廣泛的理論和實驗研究基礎, 可定性地表征水滴在固體表面的潤濕模擬[22,29].液滴的初始結構為類固體原子排布的面心立方晶格晶格結構, 在體系溫度下的飽和密度為1.31 × 103kg/m3, 晶格常數為1.72σ.初始狀態, 氬原子全部設置為液體原子, 相空間中氣相氬原子數目為零.根據納米尺度與原子尺度量級的比較(D≥ 10σ), 本模擬中液滴直徑選取D=26σ(8.86 nm)[25,27], 原子數量為7131個, 對應的液滴體積為364.2 nm3.

圖1 (a)初始狀態下的模擬系統圖; (b)系統俯視圖; (c) 納米結構示意圖Fig.1.(a) Diagram of a simulated system in initial state; (b) top view of system; (c) schematic diagram of nanostructure.

前文依據Wenzel[8]及Cassie和Baxter[9]的理論分別給出了粗糙度因子r及相面積分數f的定義, 并在圖2(a)—(c)中利用不同顏色的線段顯示, 其中Asl代表固-液實際接觸面積,Alv代表氣-液接觸面積,Apr代表投影面積.下面結合圖2(d)對相關參數作如下設定, 黑色虛線包圍區域作為一個單元, 單個納米結構頂部寬度設為w, 即上表面圓直徑, 高度設為h, 相鄰柱間頂部寬度為s, 納米結構傾角為φ, 粗糙因子r及相面積分數f計算如下:

圖2 (a) Cassie, (b) Partial Wenzel, (c) Wenzel潤濕狀態的示意圖; (d)粗糙度因子r及相面積分數f確定的示意圖Fig.2.Sketches for (a) Cassie, (b) Partial Wenzel and (c) Wenzel wetting states; (d) schematic diagram for determining roughness factor r and phase area fraction f.

將各結構的幾何參數代入(3)式和(4)式, 可得不同φ的粗糙因子r和相面積分數f, 具體見表1.

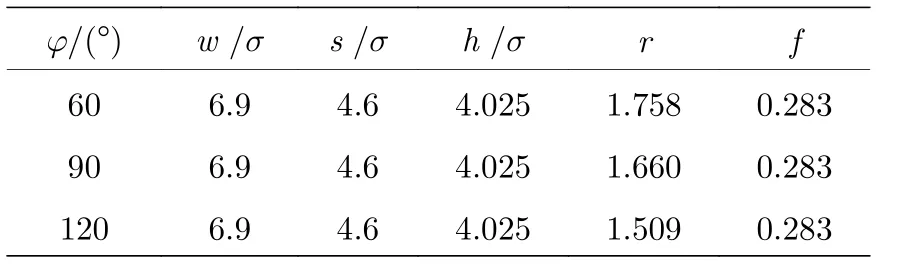
表1 三種粗糙表面對應的結構參數Table 1.Structural parameters corresponding to three rough surfaces.

2.2 模擬體系控制方程

不同種原子間的相互作用采用修正后的LJ勢能模型, 表達式為[30]

式中r為原子間距, 由Lorentz-Berthelot守則[31]可得能量參數特征尺寸σsl=(σs+σl)/2.調節能量系數α和尺度系數β可以改變固-液間的相互作用力, 得到不同的浸潤性.其中不同類型的原子對應的特征尺寸分別為σs=0.2475 nm,σl= 0.3405 nm; 能量參數分別為εs=8.35 × 10—20J,εl= 1.67 × 10—21J.模擬過程中的截斷半徑設為3.0σ.對于距離大于3.0σ的原子, 原子間相互作用可忽略不計.

采用Velocity-Verlet算法求解運動方程, 時間步長取Δt= 0.002346τ, 其中為LJ約化時間常數.模擬過程對系統采用正則系綜(NVT), 維持體系溫度為定值T= 0.827ε/kB,kB為玻爾茲曼常數, 采取Langevin方法控溫.體系運行100萬步(對應時間5 ns)后達到平衡.為保證數據的有效性, 平衡后再繼續運行100萬步對相關結果進行統計平均.

通過調節固-液勢能參數(α和β)可以改變表面浸潤性, 圖3(a)為體系內無量綱勢能隨粒子間距的變化曲線.勢能φ隨原子間距r的增大先減小后增大, 最后趨于穩定.勢阱深度代表固體原子對液體原子的束縛程度, 隨固-液勢能參數的增大而增大.當吸收的能量不足以克服勢能壁壘的限制時, 液體原子在平衡位置附近振動, 呈類固體排列.圖3(b)為本征接觸角θe(液滴站立在光滑表面上時, 在氣-液-固三相交點處作氣-液界面切線, 此切線與固-液界線間的夾角)隨固-液作用參數β的變化曲線.結果顯示,θe與β呈線性關系.本文選取了七種不同的浸潤性,α= 0.14,β分別為0.3,0.35, 0.4, 0.45, 0.5, 0.55和0.6, 對應的θe分別為157.6°, 143.5°, 129.4°, 114.5°, 101.3°, 84.6°和68.9°.

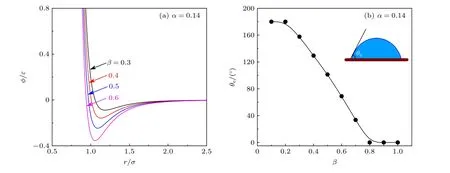
圖3 (a)無量綱勢能隨粒子間距的變化曲線; (b)本征接觸角隨表面浸潤性的變化曲線Fig.3.(a) Variation curves of dimensionless potential energy with particle spacing; (b) change curves of intrinsic contact angle with surface wettability.

2.3 接觸角的標定

圖4 給出了三種潤濕模式下液滴的密度云圖及接觸角測量方法.不同顏色表示不同的數密度范圍, 通過擬合連接氣-液界面的等密度點, 得到等密度曲線, 圖中藍色實線代表液體主體密度與氣體主體密度的平均值, 即ρ*= (ρl+ρv)/2.紅色區域代表固體基板與納米結構, 藍色虛線代表對氣-液界面進行圓形擬合得到的液滴外形輪廓線.不同潤濕模式均選取納米結構頂部與液滴接觸部分作為測量基準(圖4(d)—(f)中黑色實線所示), 與液滴外部輪廓線做切線, 與水平面夾角即為液滴在粗糙表面的表觀接觸角θ, 簡化表達統一寫成接觸角.圖4(e)中標示的D代表液滴在粗糙表面的滲透深度, 滲透深度與納米結構高度之比為滲透率P, 表示液滴的潤濕程度.采用文獻[32]中液滴潤濕狀態的劃分方法, 以潤濕程度P區分液滴潤濕狀態, 其中Cassie模式,P≤ 20%; Wenzel模式,P= 100%;Partial Wenzel模式, 20% ＜P＜ 100%.

圖4 液滴在粗糙表面上三種潤濕模式下的(a)—(c)密度云圖及(d)—(f)接觸角Fig.4.(a)—(c) Density nephograms and (d)—(f) contact angles of droplets in three wetting modes on rough surfaces.

3 結果與討論

3.1 表面浸潤性及納米結構傾角對接觸角的影響

納米液滴在潤濕過程中, 表面張力和分子間作用力是液滴變形與移動的驅動力, 控制液滴在垂直及水平方向的移動.初始模擬環境為真空狀態, 由于空間內壓差及分子間力的作用, 在液滴演化過程中, 氬原子逐漸離開液滴進入氣相區域發生擴散,隨著氣相原子數目不斷增多, 氣相空間壓力趨于飽和, 液滴處于穩定狀態.圖5(a)—(c)代表不同θe和φ對應的液滴潤濕平衡位型圖.當θe= 157.6°時, 液滴潤濕過程中固-液接觸面積較小, 導致表面張力在垂直方向的分量遠大于固-液相互作用力,使得液滴無法穩定在固體表面而發生脫離(Dewetting狀態).王文輝[33]研究結果中也提到了類似的現象.

為表示不同φ和θe下液滴在固體表面的潤濕程度, 圖5(d)給出了滲透率(P)隨浸潤性(θe)的變化曲線.隨著θe的減小, 分子間作用力逐漸占主導地位,P由0增至100%, 液滴逐漸向Wenzel模式過渡.隨著φ的減小,P不斷減小, 一定程度上降低了液體原子向納米結構凹槽滲透的能力.

圖5 (a)—(c)當φ = 60°, 90°, 120°時, 不同θe的平衡狀態位型圖; (d) 當φ = 60°, 90°, 120°時, 滲透率隨表面浸潤性的變化曲線Fig.5.(a)—(c) Bitmaps of equilibrium states for different θe with φ = 60°, 90°, 120°; (d) permeability curves with surface wettability with φ = 60°, 90°, 120°.

在宏觀實際中, 固體表面的各種微小結構對潤濕性能都會產生一定影響, 液滴在固體表面的潤濕狀態和接觸角會隨著表面浸潤性、幾何尺寸和納米結構傾角的改變而發生變化.如圖6(a)所示, 在相同納米結構傾角(φ)下, 固體表面上的θ隨著θe的增加而增加.而在相同浸潤性(θe)下, 按照潤濕模式和液體進入凹槽的數目Np(Np的統計方法為: 截取沿z方向7σ的位型圖對應的俯視圖), 可將θ隨著φ的變化劃分為I和II兩類.

在I類情況下,θ隨著φ的增加而增加.當θe=84.6° (潤濕模式與Np相同)時, 液滴在固體表面呈Wenzel狀態(圖5(a)—(c)所示), 對應的Np= 4(圖6(b)所示), 此時θ60°＜θ90°＜θ120°.造成上述現象的原因是, 單個凹槽的體積隨著φ的增加而減小, 導致納米結構內部可容納的總原子數(Ntotal)隨φ的增加而減小(圖6(c)所示).

在II類情況下,θ隨著φ的增加而減小.當θe= 129.4°(潤濕模式不同、Np相同)時, 隨著φ的增加, 潤濕模式依次為Cassie, Partial Wenzel和Partial Wenzel, 對應的Np= 1 (圖6(b)), 此時,θ60°＞θ90°＞θ120°.主要原因為:φ對液體原子向凹槽內部的滲透能力有一定影響, 且Ntotal隨著φ的增加逐漸增加(圖6(c)); 當θe= 101.3° (潤濕模式相同、Np不同)時, 液滴在固體表面呈Wenzel狀態(圖5(a)—(c)), 對應的Np,90°=Np,120°= 4和Np,60°= 1 (圖6(c)), 此時,θ60°＞θ90°＞θ120°.造成上述現象的原因是: 當液滴外緣位于納米結構邊緣時, 高的表面邊緣密度導致近壁面處接觸線固定, 限制了液體原子的水平移動.

圖6 (a)當φ = 60°, 90°, 120°時, 表觀接觸角隨θe的變化曲線; (b)液體潤濕凹槽數目隨θe的變化曲線, 其中, φ = 90°和120°時的曲線完全重合; (c)液體原子滲入到凹槽的數量隨θe的變化曲線; (d)液滴基底圓半徑隨θe的變化曲線Fig.6.(a) Curves of apparent contact angle with θe when φ = 60°, 90°, 120°; (b) change curves of the number of liquid wetting grooves with θe, where the curves at φ = 90° and 120° are completely coincident; (c) amount of liquid atoms entering the groove varies with θe; (d) change curves of the droplet base circle radius with θe.

此外由圖6(d)可知, 對于相同納米結構傾角(φ)的固體表面, 基底圓半徑B(指納米結構頂部固-液接觸面積對應的半徑)隨θe的減小而增大,表明浸潤性越強, 液滴在粗糙表面的鋪展程度越大.對于相同浸潤性的固體表面,B隨φ的增大而增大.但φ= 120°與60°時,B存在突降, 如圖6(d)中1和2標識所示, 其中標識2對應的表面浸潤性下, 呈現相反的變化規律.出現該現象的原因是不同φ對應的潤濕狀態或Np不同.當θe= 143.5°時(圖6(d)中的標識1),φ= 60°與90°對應的為Cassie狀態, 而φ= 120°對應的為Dewetting狀態; 當θe= 101.3°時(圖6(d)中的標識2),φ= 90°與120°對應的Np= 4, 而φ= 60°對應的Np= 1.

3.2 理論計算與MD模擬比較

3.2.1 理論自由能的計算

本節中建立三維空間內液滴在粗糙表面的潤濕模型, 假設液滴分布為球型, 每種狀態的總能量為液滴和其接觸表面之間所產生的所有能量之和.系統的自由能差可表示為

固體表面上的Young方程為

結合(6)式和(7)式得到:

(6)式對于微觀系統的能量計算同樣適用[34,35].值得指出的是, 納米尺度下重力對液滴動力學行為的影響很小, 所以本文忽略了納米液滴的重力.即公式中的重力項Fg= 0.其中, ΔEint為固體表面上有無液滴時的固-液-氣界面能差值;Eg為重力勢能;σlv為氣-液表面張力,Alv為氣-液接觸面積,Asl為固-液接觸面積.

對于Cassie模型:

對于Wenzel模型:

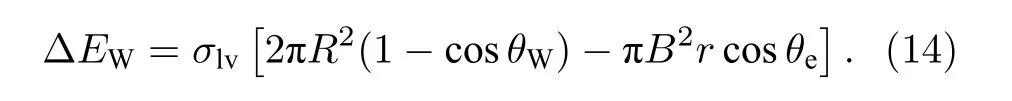
這里R為液滴半徑,B為基底圓半徑, 表達式為

3.2.2 理論預測與模擬結果的比較

圖7(a)—(c)為理論自由能的計算結果, 且對比MD模擬結果(圖5), 發現二者符合較好.當θe= 129.4°,φ= 90°時, 理論預測結果顯示ΔEW＞ ΔEC, 基于自由能最低原理判斷液滴呈Cassie潤濕模式, MD模擬結果同樣得出該表面浸潤性下液滴呈Cassie潤濕模式.

圖7 (a)—(c)不同φ和θe下的理論自由能值; (d)—(f)不同φ和θe下接觸角的變化Fig.7.(a)—(c) Theoretical free energy values under different φ and θe; (d)—(f) change of contact angle under different φ and θe.

由圖7(d)—(f)發現,θ隨θe增加而增加, 變化趨勢與φ無關, 但數值上存在略微差別.通過對處于C (Cassie)和W (Wenzel)兩種區域內的模擬值(θSIM)與對應潤濕模式的預測值(θC,θw)進行比較, 發現在不同φ值下,θC都近似等于θSIM; 在大多數情況下θw與θSIM符合良好.但θe= 68.9°時θSIM＞θw, 此時液滴外緣位于納米結構邊緣(圖5), 高表面邊緣密度使得接觸線固定, 釘扎作用顯著, 但Wenzel與Cassie理論模型未考慮上述釘扎效應的影響, 所以理論預測值偏小.而處于PW (Partial Wenzel)區域的θSIM與θC,θw的大小關系為θw＜θSIM＜θC, 且滲透程度越高,θSIM越接近θw.通過理論公式計算的C與W潤濕模式的轉換接觸角θCW近乎相等(θCW,60°= 123.6°,θCW,90°= 121.4°,θCW,120°=125.8°), 均位于PW區域.

3.2.3 不同浸潤性及納米結構傾角下的潤濕模式分區

為了討論不同θe和φ對潤濕模式的影響, 對潤濕模式進行統計(如圖8所示).研究發現, 可將φ-θe相圖劃分為4個區域: C, W, PW和DW(Dewetting), 隨著θe的增加, 液滴逐漸實現W→PW→C→DW的潤濕轉換.

圖8 不同φ和θe下的潤濕模式分區圖Fig.8.Wetting mode partition diagram under different φ and θe.

在60° ＜θe＜ 118°時, 液滴在納米結構表面呈現W狀態, 該潤濕狀態在相圖中占比最高, 約為總區域面積的1/2, 在該區域內表面浸潤性占主導作用(即固-液間作用力較強).隨著θe的增加(125° ＜θe＜ 145°), 液滴在納米結構表面呈現C與PW狀態, 且C與PW區域分別呈三角形和反梯形分布, 兩種潤濕區域所占面積近乎相等.其中C區域面積隨φ的減小而增大, 表明φ減小增強了由銳邊效應引起的釘扎作用, 使得壁面外緣可以容納更多的流體原子; 但當φ較大時(φ≥120°)不存在C狀態, 微柱陣列表面的液體原子在毛細力和固-液相互作用力[27]的共同作用下, 更容易滲透至納米結構內部, 不利于形成超疏水表面.在θe＞ 145°時, 液滴在納米結構表面呈現DW狀態, 表面張力占主導作用(即固-液間作用力較弱), 且發現在該區域內固體原子數目隨φ的增加而增加.

4 結 論

采用MD方法研究不同納米結構傾角(φ)及表面浸潤性(θe)下, 結構尺寸與液滴大小相當時,納米氬液滴在粗糙鉑表面的潤濕行為.討論表觀接觸角的影響因素及檢驗是否符合Wenzel及Cassie理論預測模型[8,9], 根據不同結構及浸潤性進行潤濕模式分區.具體結論如下:

1)液滴在不同納米結構傾角(60°, 90°和120°)及浸潤性的表面達到潤濕平衡后存在四種潤濕狀態, 分別為Dewetting, Cassie, Partial Wenzel和Wenzel, 隨著表面浸潤性的減弱, 潤濕狀態逐漸由Wenzel向Dewetting過渡;

2)通過比較表觀接觸角模擬值(θSIM)與理論預測值(θw,θC)的大小關系, 發現不同納米結構傾角在Cassie與Wenzel潤濕狀態的表觀模擬值與預測值基本符合, 而Partial Wenzel潤濕狀態由于部分液體原子滲入凹槽內, 模擬值較預測值偏小(θSIM＜θC), 且滲透程度越高θSIM越接近θw;

3)不同潤濕模式基本滿足自由能最小原理,根據φ和θe對潤濕模式進行分區: 隨著浸潤性θe的減小,φ對最終潤濕狀態的影響減弱, 尤其當θe＜ 118°時, 液滴在納米結構表面均呈Wenzel狀態; 對于超疏水表面(118° ＜θe＜ 145°), 倒梯形(φ= 60°)納米結構有利于保持Cassie狀態, 而正梯形(φ= 120°)納米結構容易形成Partial Wenzel液滴, 其一由于φ減小增強了銳邊效應引起的釘扎作用, 相同浸潤性下降低了液體原子向凹槽內滲透的能力, 其二是當液滴擴散至納米結構外緣時,可以容納更多的流體原子.