超冷長程Rydberg-基態分子*

白素英 白景旭 韓小萱 焦月春2) 趙建明2)?

1) (山西大學激光光譜研究所, 量子光學與光量子器件國家重點實驗室, 太原 030006)

2) (山西大學極端光學協同創新中心, 太原 030006)

3) (太原師范學院物理系, 晉中 030619)

1 引 言

長程Rydberg-基態分子是由一個Rydberg原子與一個或多個基態原子形成的一類奇異的分子,具有尺寸大(～μm)和永久電偶極矩大(～kilo-Debye)等性質.這種奇異分子的束縛機制是Rydberg電子與中性原子之間的低能散射相互作用,是不同于共價鍵、離子鍵及范德瓦耳斯相互作用的一種新型束縛機制.

低能散射相互作用的研究可追溯到20世紀30年代.1934年, Amaldi和Segré[1]在Rydberg原子碰撞實驗中發現了與預期不同的結果, 即: 在鈉或鉀的蒸汽中充入H2和N2等氣體的實驗中,并沒有觀察到預期的Rydberg原子吸收譜線由于碰撞導致的展寬, 而是譜線的頻移.這一現象無法用已知的理論進行解釋, 他們在與Fermi的討論中發現, 這些能級的頻移是由堿金屬原子的價電子與外部氣體原子散射引起的.隨后Fermi發展了量子散射理論并在該理論中引入了散射長度的概念, 導致Fermi贗勢(Fermi pseudopotential)[2]的產生.在Fermi的理論中只考慮了s-波散射相互作用,1977年, Omont[3]發展了這一理論并考慮了任意高階波散射, 完善了中性原子的散射理論.2000年,Greene等[4]首次在理論上預言了超冷長程Rydberg-基態分子的存在, 理論上計算了銣Rydberg-基態分子的絕熱勢能曲線, 并獲得了巨大的分子永久電偶極矩.計算的電子波函數概率密度呈三葉蟲型,因此這類分子被稱為三葉蟲型分子[4].不久, 理論學家又預測出形如蝴蝶狀的電子波函數概率密度的分子, 被稱為蝴蝶型分子[5,6].

2009年, Bendkowsky等[7]首次在實驗中成功觀測到s-波散射形成的超冷RbnS態Rydberg-基態分子.之后, 其他研究小組分別觀測到了Rb原子nP1/2,3/2[8]和nD3/2,5/2[9-11]態以及Cs原子nS1/2[12,13],nP3/2[14]和nD3/2,5/2[15-17]的Rydberg-基態分子.近年來, 人們在實驗中觀測到了p-波共振形成的內層勢阱分子[18,19].2020年, Peper和Deiglmayr[20]提出一種超冷原子離子對態的激發方式, 提出了一種形成heavy-Rydberg態[21]的新方法.由于Rydberg-基態分子的尺寸大且具有巨大的永久電偶極矩, 使得這類分子成為研究量子模擬[22]和量子信息過程[23-25]的理想介質.

本文主要介紹Rydberg-基態分子的束縛機制和實驗研究成果, 包括Rydberg電子與基態原子低能電子散射的理論模型、Fermi贗勢和Rydberg-基態分子的絕熱勢能曲線、光締合光譜及永久電偶極矩的測量等.

2 低能電子散射的理論模型

在Rydberg電子與基態原子相互碰撞散射過程中, 基態原子被視為微擾, 其散射相互作用勢能由Fermi贗勢描述[2,3].圖1為散射相互作用的示意圖, 在以Cs+離子為參考的坐標系中, 散射相互作用能表示為[3]

圖1 Rydberg-基態分子示意圖.自旋為 的Rydberg電子和基態原子分別位于以Cs+離子為參考系的位置r和Rz?處.分別是基態原子的電子自旋和核自旋Fig.1.Schematic of the molecular system.The Rydberg electron with spin sits at position r relative to the ionic core.A cesium ground state atom is located at positionRz? relative to the ionic core of the Rydberg atom. andare electronic and nuclear spin of the ground state atom,respectively.

其中,r和Rz＾ 分別是Rydberg電子和基態原子相對Cs+離子的位置,as(k) 為s-波散射長度,ap(k)為p-波散射長度,δ為δ函數,?表示梯度算符,k是Rydberg電子的動量.散射長度al(k) 與能量有關, 表示為al(k)2l+1=-tanηl(k)/k2l+1, 其中,l為散射波階數,l= 0或1表示s-波或p-波散射,ηl是散射相移.

Rydberg原子與基態原子相互作用的總哈密頓量表示為[26]

將(2)式在核間距R上進行對角化可得到分子絕熱勢能曲線[4,7].分子的振動態和轉動態可通過分子哈密頓理論[27-29]計算獲得.對于雙原子Rydberg-基態分子來說, 可以通過相應的絕熱勢能曲線準確地獲得振動態和振動波函數.多原子分子[30-33]卻很難獲得準確的振轉能級.

圖2所示為理論計算的n= 19附近的Cs Rydberg-基態分子的勢能曲線.處于700a0附近(標注I)的外層勢阱主要由三重態3s-波散射形成,對應的電子波函數概率密度形如三葉蟲, 見插圖I,這類Rydberg-基態分子稱為“三葉蟲型”分子[4].處于200a0—400a0附近(標注II)的內層勢阱, 主要由三重態3p-波散射形成, 對應的電子波函數概率密度形如蝴蝶狀, 見插圖II, 這類Rydberg-基態分子稱為 “蝴蝶型”分子[5,6].“蝴蝶型”分子的勢阱深度比“三葉蟲型”分子深, 而平衡核間距小.圖2中的電子波函數中(插圖)黑色點表示Cs離子, 藍色點表示基態原子.

圖2 理論計算的n =19附近的Cs分子勢能曲線, 其中插圖是橙色原點標記I (II)處勢阱對應的“三葉蟲型”(“蝴蝶型”)分子的電子概率密度Fig.2.Calculations of potential energy curves of the Cs Rydberg-ground molecule near n = 19.Inset I (II) displays the electronic wave function densities of “Trilobite” (“Butterfly”) molecules at the orange points marked I (II) in the figure.

這里主要考慮最外層勢阱形成的三葉蟲型分子.以銫原子37D5/2+ 6S1/2形成的分子為例進行說明, 對應的勢能曲線如圖3所示[17].圖3中虛線所示的勢能曲線是只考慮s-波散射的結果, 包含兩個勢阱, 深勢阱(TΣ)主要由s-波自旋三重態T(3s)散射形成, 淺勢阱(STΣ)由s-波自旋單態S和自旋三重態T的超精細結構混合形成.圖3的實線表示同時考慮s-波和p-波散射時的絕熱勢能曲線.從圖3可以看出, p-波散射對勢能曲線的最外層勢阱幾乎沒有影響, 因此s-波散射可以很好地描述分子勢能曲線最外層勢阱的性質.然而, p-波散射對內層勢阱有較大的影響, 使內層勢阱的阱深顯著增加, 如圖3中核間距R＜ 1800a0處的勢阱.以p-波散射為主形成的分子的電子波函數概率密度形如蝴蝶狀, 如圖2所示, 形成的Rydberg-基態分子叫作“蝴蝶型”分子[5,6].

圖3 數值計算的37D5/2 + 6S1/2 (F = 4) Rydberg-基態分子的絕熱勢能曲線.深勢阱(灰色線)主要由自旋三重態T形成, 淺勢阱(藍色線)主要由自旋單態S和自旋三重態T超精細結構混合而形成.實線和虛線分別是考慮和不考慮p-波散射相互作用時的分子絕熱勢能曲線.彩色填充線分別是最外層深勢阱TΣ (v = 0)和TΣ (v = 1)的振動波函數,黑色填充線是最外層淺勢阱STΣ (v = 0)的振動波函數[17]Fig.3.Calculations of potential energy curves of the Rydberg-ground molecule that is asymptotically related to the 37D5/2 Rydberg atomic line with (solid lines) and without(dashed lines) taking the p-wave scattering interaction into account.The deep potential (gray) for the triplet state and shallow wells (blue) for hyperfine-mixed singlet-triplet potential state.The vibrational wave functions in the outmost wells are indicated in filled curves for TΣ (v = 0) and TΣ (v = 1) of deep potential and STΣ (v = 0) of shallow potential[17].

基態原子的超精細結構F對Rydberg分子的最外層深勢阱TΣ態幾乎沒有影響, 但是淺勢阱STΣ態的阱深則與基態原子所處的超精細結構有關.以Cs原子為例, 如圖4所示[16].圖4(a)為理論計算的36D5/2+ 6S1/2(F= 4) (黑色虛線) 和36D5/2+ 6S1/2(F= 3) (青色實線) 的分子勢能曲線.深勢阱對應的勢能曲線主要由自旋三重態3s-波散射形成, 對于基態原子處于F= 4和F= 3的超精細能級, 深勢阱TΣ態的勢阱深度相同, 不隨基態原子的超精細能級的變化而變化; 淺勢阱對應的勢能曲線由單重態1s和三重態3s-波散射混合形成, 淺勢阱STΣ態的勢阱深度依賴于基態原子所處的超精細能級, 即基態原子處于超精細能級F= 3的勢阱深度大于F= 4的勢阱深度.

圖4 (a) 數值計算的Cs原子36D5/2 + 6S1/2 (F = 4)(黑色虛線)和36D5/2 + 6S1/2 (F = 3)(青色實線) Rydberg-基態分子的絕熱勢能曲線.深勢阱(TΣ)主要由自旋三重態T的s-波散射形成, 勢阱深度不隨基態原子的超精細能級F的變化而變化.淺勢阱(STΣ)主要由自旋單態S和自旋三重態T超精細結構混合而形成, 其勢阱深度與基態原子所處的超精細能級F有關, 基態原子處于超精細能級F = 3的勢阱深度大于F = 4的勢阱深度.彩色的實線表示v = 0的振動波函數.(b), (c)為實驗測得的36D5/2 + 6S1/2 (F = 4)和36D5/2 + 6S1/2 (F = 3)的光締合光譜.實心(空心)三角表示由淺勢阱(深勢阱)形成的分子信號.黃色線是高斯擬合曲線[16]Fig.4.(a) Calculations of potential energy curves (PECs)for 36D5/2 + 6S1/2 (F = 4) (black dashed lines) and PECs for 36D5/2 + 6S1/2 (F = 3) (cyan solid lines) molecules, respectively.The deep potentials (TΣ) mostly arise from triplet s-wave scattering and do not depend on F.The shallow potentials (STΣ) mostly arise from mixed singlet-triplet s-wave scattering and depend on F; The potential energy curves for F = 3 is deeper than that for F = 4.The colored lines show the v = 0 vibrational wave functions of the potential energy curves.(b), (c) Experimental photo-association spectra for 36D5/2 + 6S1/2 (F = 4) and 36D5/2 + 6S1/2(F = 3) molecules.Filled (open) triangles mark the molecular signals formed by mixed (triplet) potentials.The yellow lines display Gaussian fittings[16].

實驗上對淺勢阱和深勢阱形成的分子的束縛能的精確測量, 可以提供對s-波單態和三重態散射相移及散射長度的精確萃取.因此, 長程Rydberg-基態分子可以作為高精度的散射實驗材料制備, 以及用于探測超慢電子-原子碰撞(電子能量低于10 meV)實驗, 這是通過電子傳輸[34]等方法難以實現的.通過長程Rydberg-基態分子已經實現了s-波相移[14,35,36]和p-波相移[11,18,35,37]的測量.

3 Rydberg-基態分子的光締合光譜

3.1 雙原子Rydberg-基態分子

Bendkowsky等[7]于2009年首次在實驗上觀測到了銣原子主量子數取值為n= 34—40的長程Rydberg-基態分子, 并對分子壽命以及分子在外電場作用下的Stark頻移進行了測量.圖5是實驗測量的銣原子n= 35—37 S態Rydberg-基態分子的光締合光譜[7], 在相對于原子共振負失諧處獲得了非常明顯的分子信號, 他們用s-波散射理論解釋了實驗結果.之后, 人們又實現了不同原子種類和同位素(133Cs,84Sr,87Sr,85Rb)以及不同電子態(P態和D態)的長程Rydberg-基態分子的實驗觀察[9-11,13,16,17,38-42].實驗上, 人們用光締合的方法對雙原子(一個Rydberg原子和一個基態原子)Rydberg-基態分子進行制備, 所要求的冷原子密度在1010—1013cm—3量級.

圖5 實驗測量的Rb nS + 5S (n = 35—37) Rydberg-基態分子的光締合光譜.左圖是右圖灰色部分的放大[7]Fig.5.Measured spectra of nS + 5S (n = 35—37) of Rb atoms.The left panel shows the enlarged view of the gray area on the right[7].

圖4為實驗測量的Cs原子36D5/2+ 6S1/2的光締合光譜線與理論計算的勢能曲線的對比.圖4(b)和圖4(c)是實驗測量的雙光子光締合光譜, 對應基態原子分別處于超精細結構F= 4和F= 3.圖中灰色的點是原始實驗數據, 黑色線是實驗數據的15次平均值, 黃色線是對分子信號進行高斯擬合的結果.圖4(a)是理論計算的絕熱勢能曲線.黑色虛線和青色實線分別是基態原子處于F= 4和F= 3的勢能曲線, 紅色、藍色和粉色實線分別表示勢能曲線的振動基態(v= 0)波函數.實驗測量與第二部分所述的低能電子散射理論的計算結果相符合, 基態原子的超精細結構使基態原子為F= 3的淺勢阱(STΣ)比基態原子為F= 4時的勢阱深, 而深勢阱(TΣ)的勢阱深度不隨基態原子的超精細結構變化.

3.2 多原子Rydberg-基態分子

長程Rydberg-基態分子是在高密度的冷原子樣品中通過光締合的方法制備的.當密度足夠大時, Rydberg電子可與多個基態原子散射形成多原子Rydberg-基態分子[43].關于多原子Rydberg-基態分子[43]的文獻介紹了包含2個、3個和4個基態原子的Rydberg-基態多聚體.在這種情況下得出的一個重要結論是三原子的Rydberg-基態三聚體形成穩定的環狀結構, 但相應的二聚體(雙原子分子)卻相互排斥[44].由于選擇定則的限制, 通過光締合的實驗方案很難實現高-?Rydberg態的激發, 因此隨后的大多數實驗和理論工作都集中在低-?(?≤ 2)的Rydberg-基態分子.

在實驗上觀測到二聚體Rydberg-基態分子后不久, 人們就觀測到了三聚體的光締合光譜[35], 以及四聚體、五聚體和六聚體的Rydberg-基態分子[45].研究表明, 這些多原子聚合物的結合能與基態原子數成線性比例關系, 即結合能是二聚體結合能的整數倍.圖6是Rb (nS) 態的多原子Rydberg-基態分子光締合光譜, 其中多原子分子線由彩色菱形標記[45].如圖6所示, 三聚體(紫色菱形)是二聚體(紅色菱形)結合能的兩倍, 因為兩個基態原子都以能量最低的二聚體模式被Rydberg電子束縛.這種構造原理后來被推廣到殼結構模型[46].

圖6 不同主量子數n 的Rb (nS)多原子Rydberg-基態分子的光締合光譜, 其中多原子分子的譜線由彩色菱形標記[45]Fig.6.Photoassociation spectra of polyatomic Rb (nS) ultra-long Rydberg-ground molecules for different principal quantum numbers n.Polyatomic lines are marked by colored diamonds[45].

圖6所示為原子密度等于1012cm—3且在不同主量子數n下測得的多原子Rydberg-基態分子的光締合光譜.當主量子數n≤ 71時, 可以很好地區分多原子Rydberg-基態分子的信號, 但對于更大的主量子數n的多聚體, Rydberg電子軌道內基態原子數目以n6增加, 而束縛能卻以n—6減小.在這種情況下, 實驗光譜顯示了一個碰撞加寬的Rydberg譜線而不是分離的分子共振線, 如圖6中n= 111的情況.在平均場極限下, 碰撞加寬的譜線呈現出與原子Rydberg態有一定失諧的高斯峰[1,47,48], 這一現象可由Fermi[2]理論進行解釋,對應的失諧量由所有基態原子的平均相互作用能給出:

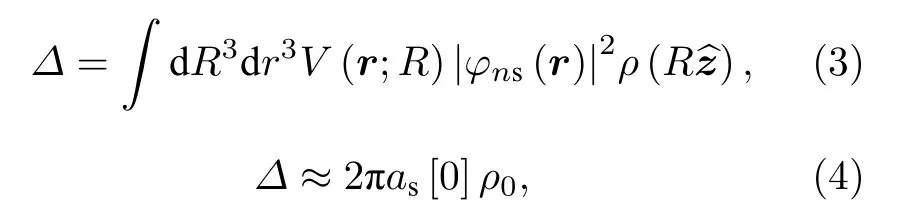
其中,φns(r) 是Rydberg電子波函數,ρ(Rz?) 是原子密度.假設ρ(Rz?)=ρ0, 且將電子-原子相互作用V(r;R)用s-波散射相互作用在零能極限下的s-波散射長度as[0] 代替, 即可得到(4)式.(4)式的廣義形式包括與能量有關的散射長度、p-波的貢獻以及不均勻的原子密度.

無論實驗還是理論, S-態Rydberg系統都具有一定的優勢: 1) S-態的各向同性可以使理論模型得以簡化; 2)較大的Franck-Condon因子在實驗上產生較大的激發概率.相反,?＞ 0的態Franck-Condon因子相對減小, 由于原子的各向異性和基矢所需的更大的希爾伯特空間, 使高?態的Rydberg-基態分子難以實現精確的理論描述.但高?態的復雜性可以導致更豐富的物理特性.特別是?＞ 0的多原子Rydberg-基態分子的Born Oppenheimer勢能曲面與角度相關, 即這些勢能曲面不僅取決于基態原子的徑向距離, 還取決于基態原子間的相對角度[15,49-51], 使高?態的Rydberg-基態分子具有豐富的光譜特性.

4 Rydberg-基態分子的永久電偶極矩

分子的電偶極矩對化學反應精確控制[52,53]、精密光譜測量、實現量子模擬[22]、量子信息處理[23]及基本對稱性測試[53]等方面具有重要意義.分子的永久電偶極矩是對稱性破缺的體現, 因此, 同核分子一般不具有永久電偶極矩, 但Rydberg-基態分子是例外, 這類分子具有永久電偶極矩, 且達到約kilo-Debye量級[4,12].

2011年, Li等[54]首次測量了Rb原子nS態長程Rydberg-基態分子的永久電偶極矩, 測量結果為1 Debye, 與理論計算符合得很好; 測量的Rb原子25P態勢能曲線附近的蝴蝶型分子的永久電偶極矩約為500 Debye[55].2015年, Booth等[12]測量了Cs原子nS態的Rydberg-基態分子的永久電偶極矩, 其值高達～2000 Debye, 圖7所示為對應的實驗結果.由于Cs原子nS態的量子虧損為4.05, 接近于整數, 因此nS Rydberg態具有非常接近類氫原子的勢能曲線, 使高-?的三葉蟲型分子的勢能曲線與nS態交叉.三葉蟲分子態是高角動量量子態, 根據角動量守恒一般不能由單光子或者雙光子激發獲得三葉蟲分子態, 但由于銫原子三葉蟲型分子的勢能曲線與nS態之間的這種交叉, 使得在Cs原子中三葉蟲型分子混合了S-態特性, 導致nS態Rydberg-基態分子具有巨大的永久電偶極矩.

圖7 (a) 理論計算的Cs nS + 6S (n = 37, 39, 40) TΣ+態電子波函數密度[12]; (b) 相應于(a)圖的勢能曲線和振動能級[12]; (c)為(b)圖中箭頭標注的振動能級在外電場中分子譜線的展寬[12]Fig.7.(a) Calculated densities of electron wave functions for the TΣ+ states of Cs nS + 6S (n = 37, 39, 40)[12]; (b) the corresponding potential energy curves for the states shown in panel (a) with calculated vibrational levels[12]; (c) the broadening of the vibrational levels indicated by an arrow in panel (b) as a function of applied electric field[12].

研究表明這些分子的永久電偶極矩都是正的[12-14,56], 這說明Rydberg電子波函數在微擾原子附近是干涉相長的.2020年, Bai等[16]在實驗上制備了CsnDJ+ 6S1/2Rydberg-基態分子并測量了其永久電偶極矩.理論模擬結果顯示, CsnD態Rydberg-基態分子的永久電偶極矩是負值, 這與文獻報道的研究結果不同.偶極矩的負值反映了在基態(微擾)原子附近的Rydberg電子密度的減少,這是由電子結構混合引起的.

實驗上可通過測量分子信號在弱電場作用下的分子譜展寬實現對電偶極矩d的測量.Rydberg分子在弱電場中的能量表示為(-d·E)(E為電場強度), 遠小于分子束縛能.這時分子信號在弱電場中將沿分子信號中心產生非均勻展寬, 對應的展寬由矩形函數 2dE/h表示.考慮到激發光線寬和原子云處的電磁場的非均勻性等因素, 實際測量的分子信號并不是理想的矩形線型.為了獲得分子信號的展寬信息, 我們將無外場時信號的高斯線型函數與矩形函數 2dE/h進行卷積運算獲得實際光譜的線型函數, 進而獲得Rydberg-基態分子的電偶極矩.弱電場中Rydberg-基態分子的線型S(Δf) 是激發光失諧量 Δf的函數, 表示為

其中,h為普朗克常數;σf為高斯線型的標準差, 由高斯擬合無外電場時的分子信號獲得.(5)式中電場E可以通過Rydberg原子Stark光譜準確測得,只有一個待定參數, 即偶極矩d.由(5)式擬合實驗測量的外場中的Rydberg分子譜即可獲得偶極矩d的值, 進而實現Rydberg-基態分子永久電偶極矩的測量.圖8左側為不同電場下的光締合譜線, 分子譜的線寬隨著電場的增加而增加.圖8右側給出了電場為E= 0.37 V/cm時深勢阱(TΣ)和淺勢阱(STΣ)分子振動基態v= 0的譜線、(5)式的擬合結果以及測得的電偶極矩|d|值.對于圖8所示的n= 37的TΣ (v= 0)分子態的振動基態,實驗測量的平均偶極矩為d= (4.79 ± 0.78)ea0,與理論計算的結果dTheor.= —4.64ea0符合得很好.

圖8 不同電場E下的37D5/2 + 6S1/2 (F = 4) Rydberg-基態分子的光締合光譜.分子信號在外電場的作用下向藍失諧處平移,且在電場E ≥ 0.27 V/cm時開始展寬.右圖是放大的E = 0.37 V/cm下的分子信號, 紅色實線是理論擬合線[16]Fig.8.Spectra of 36D5/2 + 6S1/2 (F = 4) Rydberg-ground molecules with indicated electric fields E.The molecular peaks are blue shifted by E and substantially broadened in fields E ≥ 0.27 V/cm.The right panel shows zoom-ins of molecules peaks with E =0.37 V/cm.The red solid lines show model spectra[16].

我們注意到, 理論計算的銫原子nD5/2+6S1/2Rydberg-基態分子的永久電偶極矩為負值,這與文獻報道的Rydberg-基態分子類型不同(偶極矩為正)[12-14,56].在物理上, 偶極矩的符號反映了相對于基態原子的位置, 電子電荷沿分子軸移動的方向.負偶極矩對應于微擾基態原子(Cs 6S1/2)附近電子電荷的減少, 這種情況通常可以描述為Rydberg電子波函數在微擾原子附近的相消干涉,或者等效地描述為微擾原子附近的Rydberg電子軌道的線性組合(linear combination of atomic orbitals picture).

圖9給出了Cs原子D-型(偶極矩為負)和P-型(偶極矩為正) Rydberg-基態分子最外層勢阱相應的基態原子位于1500a0附近時的電子波函數概率密度.圖9上部為理論計算的31D5/2+ 6S1/2和32P3/2+ 6S1/2Rydberg分子的電子波函數概率密度, 由于Rydberg電子結構混合較弱不易區分兩者的差別, 圖9下部給出了分子波函數減去Rydberg原子波函數之后的結果.可以清晰地看出, P-型分子微擾原子附近的波函數主要表現為相長干涉, 產生正偶極矩; 而D-型分子微擾原子附近的波函數的干涉模式比較復雜, 在微擾原子周圍有相長干涉部分, 但是在距微擾原子一定距離處也有相消干涉部分.總體而言, 相消干涉占主導地位,導致了負偶極矩的產生.

圖9 Cs 31D5/2 + 6S1/2 (左) 和32P3/2 + 6S1/2 (右) Rydberg分子的絕熱電子波函數密度, 對應的基態原子位于1500a0附近(圖中點的位置).上圖為波函數密度, 下圖為分子減去原子的電子波函數密度, 白色和黑色表示密度的減少和增加[16]Fig.9.Densities of adiabatic wave functions for Cs 31D5/2 + 6S1/2 (F = 4) triplet (left) and 32P5/2 + 6S1/2 (F = 4) triplet (right),with the perturber located at ≈1500 a0 (dot).Top panel shows the wave function densities.Bottom panels shows the difference between electronic wave function densities of molecules and atoms on a linear grayscale, with white and black indicating reductions and increases by amounts shown on the gray-scale bar[16].

5 結 論

本文介紹了由Rydberg電子和基態原子低能電子散射機制形成的超冷長程Rydberg-基態分子,綜述了Rydberg電子與基態原子的散射相互作用的理論模型、數值計算的絕熱勢能曲線的特性;Rydberg-基態分子按照波函數的形狀可以分成“三葉蟲型”分子和“蝴蝶型”分子.當冷原子密度足夠大時, Rydberg電子可與多個基態原子散射形成多原子Rydberg-基態分子; 長程Rydberg-基態分子具有巨大的永久電偶極矩, 目前已知的最大電偶極矩可達到kilo-Debye.最近的文獻報道CsnDJ-型Rydberg-基態分子具有負偶極矩[16].偶極矩的負值反映了在基態(微擾)原子附近的Rydberg電子密度的減少, 這種情況通常可以描述為基態(微擾)原子附近Rydberg電子波函數的相消干涉.隨著對Rydberg-基態分子的研究, 人們將進一步加深對此類分子的認識.

除了對Rydberg-基態分子的束縛能、壽命和永久電偶極矩等固有屬性的研究之外, 研究波包在振蕩勢能曲線中的傳播是研究長程Rydberg-基態分子動力學過程的全新思路, 這為研究Rydberg-基態分子的化學反應過程奠定了基礎.對此類分子的研究不局限于堿金屬原子, 這種獨特的束縛機制適用于所有具有單通道和多通道散射的Rydberg系統.