層狀磁性拓撲材料中的物理問題與實驗進展*

孫慧敏 何慶林?

1) (北京大學物理學院, 量子材料科學中心, 北京 100871)

2) (量子物質科學協同創新中心, 北京 100871)

3) (北京大學輕元素量子材料交叉平臺和輕元素先進材料研究中心, 北京 100871)

1 引 言

層狀磁性材料能將材料的自發磁化維持至極端的二維極限[1], 例如材料的單原胞層厚度, 因此材料的磁性能通過除了磁場以外的其他手段來有效控制, 例如電場、載流子摻雜、應力[2]等, 提供了一個探索、理解和調控低維磁結構的多功能研究平臺, 因此層狀磁性材料一直備受二維材料、自旋電子學領域的關注.近十年來, 在拓撲物理領域的研究發展過程中, 發現了拓撲絕緣體[3]和以狄拉克、外爾、節線半金屬等為代表的拓撲半金屬[4-6].在這些本征非磁性拓撲材料中, 由于存在時間反演對稱性, 材料一般不呈現反常霍爾效應, 拓撲態的電子結構主要由無質量的螺旋性狄拉克費米子、無質量的手性外爾費米子等主導.有趣的是, 如果對體系引入垂直磁有序或外加強的垂直外磁場, 在狄拉克點或外爾點附近產生大的貝里曲率, 時間反演對稱性被破缺, 體系從而顯示出巨大的反常霍爾效應[7,8].因此, 這種由于電子結構的拓撲非平庸性的貢獻一般為材料主導的內稟特性, 值得注意的是拓撲平庸的電子結構也能貢獻一小部分的內稟反常霍爾效應.相對而言, 拓撲平庸材料中的凈磁矩、散射等機制則產生外稟反常霍爾效應[7].同時, 相對于體態, 這些拓撲材料的拓撲電子態普遍具有較低的載流子濃度, 受到拓撲保護, 能免疫一般的材料缺陷、雜質和局域化, 在特定條件下主導體系的輸運行為, 甚至使材料表現出新穎的量子特性.本綜述將對這些具有層狀結構的磁性拓撲材料的基本特性進行介紹, 以及回顧近年在這些材料中的重要實驗發現, 材料體系包括磁摻雜拓撲絕緣體Cr/V:(Bi,Sb)2(Se,Te)3、本征反鐵磁拓撲絕緣體MnBi2Te4系列、磁性外爾半金屬Co3Sn2S2、拓撲kagome磁體(即具有拓撲特性的kagome層狀晶格的層狀磁性材料, 包括磁性外爾半金屬Mn3Sn/Mn3Ge、磁性狄拉克半金屬Fe3Sn2/FeSn等).

值得一提的是, 具有kagome層狀晶格結構的材料雖然并非傳統意義的二維材料(即由范德瓦耳斯力堆垛的層狀材料), 由于其六角網絡結構的幾何特殊性, 自旋結構主要來源于形成kagome晶格的過渡金屬原子電子, 往往伴隨有許多新奇的物理、拓撲性質.具體而言, kagome晶格是具有共角三角形的、以六邊形為基本單元的獨特二維網格,類似于石墨烯.在晶格內, 分子間交換相互作用能形成局部自旋矩的磁耦合, 但同時晶格內存在強烈的幾何阻挫效應, 可能也會導致自旋在零溫下不呈現長程磁有序.所以, kagome晶格中的幾何阻挫效應的強弱能影響長程磁有序對自旋漲落的競爭,對材料的基態起重要作用.另外, 除了磁阻挫,kagome晶格還能容納不同類型的量子態, 例如狄拉克電子態, 在倒空間中, 兩個狄拉克能帶的交匯點在布里淵區邊界的K和K'點, 此點可以等價于石墨烯的晶格, 因此會類似地受到晶格對稱性的保護[9].但與石墨烯晶格不同的是, kagome晶格中垂直于基平面的晶面內并不包含最近鄰鍵合, 因此能在垂直于最近鄰鍵合方向上產生一個電場[10], 使自旋軌道耦合能在kagome晶格的電子結構上扮演重要的角色, 并能進一步產生拓撲非平庸的電子能帶[11,12].另外, 在電子跳躍模型中, 電子布洛赫波函數的相消干涉能夠有效地將電子束縛在kagome晶格的六角形中, 從而導致近無色散的平帶電子結構[13], 還有可能在材料中形成長程磁有序.拓撲kagome磁體在實驗上實現了眾多以往理論預測的拓撲物理, 是一類新興的拓撲自旋層狀材料.基于層狀磁性材料這一家族出發, 層狀磁性拓撲材料不僅同樣能將材料的自發磁化維持至極端的二維極限, 具有簡單的磁基本單元, 同時, 某些材料在這種極端的二維極限下往往還保留拓撲特性[14]; 還有材料能根據堆垛這些二維極限層來調控其磁性和拓撲特性, 呈現具有層數依賴關系的拓撲特性[15].最后需要說明的是, 本綜述僅包括層狀磁性拓撲材料和具有準二維結構(如kagome層狀晶格)的磁性拓撲材料, 其他材料不在本綜述的討論范圍內.

上述介紹的層狀磁性拓撲材料的構建、制備方式多樣, 大多材料都能使用傳統的合成方法制備,例如: 合成本征反鐵磁拓撲絕緣體MnBi2Te4系列可以用分子束外延法[16]、真空熔煉法[17,18]、(自助)熔劑法[19,20]、垂直布里奇曼法[21]等; 合成磁性外爾半金屬Co3Sn2S2可利用自助熔劑法[22-24]、布里奇曼法[25]、分子束外延法[26]等; 而拓撲kagome磁體中, Mn3Sn則有報道是采用直拉單晶制造法和電弧熔煉法結合的方法[27]或布里奇曼法[28]合成,Mn3Ge可以利用布里奇曼-斯托克巴杰法[29]合成,Fe3Sn2也能通過自助熔劑法[30]合成, 還能通過碘催化的方法熔煉[31], FeSn能通過化學氣相傳輸法合成[14]等.除了上述合成的體材料, 還可以利用晶體的(準)二維結構特性對塊材進行機械剝離或減薄, 得到更小的磁單元結構.可見, 高質量的層狀磁性拓撲材料基本上可以利用傳統的方法合成, 因此相對容易開展不同類型的實驗研究, 受到更為廣泛的關注, 具有一定的潛在應用前景.

2 層狀磁性拓撲材料的晶體、磁、電子結構

本節將介紹所涉及的幾種拓撲磁性層狀材料的晶體結構、磁結構、電子結構, 為后面介紹其拓撲物理效應進行鋪墊.

2.1 磁摻雜拓撲絕緣體

目前領域內研究得最多、歷史最悠久的本征拓撲絕緣體是V-VI族多元化合物(Bi,Sb)2(Se,Te)3,其晶體結構屬于六方晶系, 沿著[0001]方向, 該材料是由范德瓦耳斯力堆垛而成的二維材料, 每一層原子面上只有同族的原子(如均為V族或均為VI族), 而每一個范德瓦耳斯力層內則由兩個V族原子層與三個VI族原子層按照-VI-V-VIV-VI-的方式排列, 其中V-VI之間由不同強度的共價鍵和離子鍵結合而成, VI-VI之間則由范德瓦耳斯力結合, 稱為五原子層(quintuple layer).而磁摻雜的拓撲絕緣體是將少量過渡金屬原子取代V族元素的原子位置, 通過磁交換耦合機制產生長程磁有序, 形成磁性拓撲絕緣體.當然, 根據不同材料的合成條件和方式, 這些過渡金屬摻雜原子也有一定概率取代不同的VI族元素原子位置, 甚至形成比較復雜的缺陷、雜質, 產生局域的微觀磁結構.這種磁摻雜拓撲絕緣體往往具有長程的、垂直各向異性的鐵磁序, 即其易軸垂直于層狀解離面,居里溫度約為20—30 K[32].目前, 關于磁摻雜拓撲絕緣體的磁序機制有Van Vleck機制和Ruderman-Kittel-Kasuya-Yosida (RKKY)機制[33-35], 但根據實驗研究結果, 拓撲絕緣體表面磁結構非常復雜,單憑Van Vleck機制不能較好地解釋表面態對磁性的影響, 而體態載流子調制可能是由RKKY交換相互作用主導.所以, 目前對磁摻雜拓撲絕緣體的磁起源認為兩種機制普遍共存, 取決于材料的合成方法等條件, 且Van Vleck機制和RKKY機制互有強弱、相互制衡.磁摻雜拓撲絕緣體具有非常豐富的物理現象[8], 已經發現的效應包括量子反常霍爾效應[32]、軸子絕緣體態[36,37]、拓撲磁電效應[38]、自旋軌道矩[39,40]、拓撲霍爾效應[41,42]、馬約拉納費米子態[43]等.由于磁摻雜拓撲絕緣體的研究已經有將近10年的發展, 其基本的物理已研究得比較清楚, 本綜述將不再贅述.

2.2 本征磁性拓撲絕緣體

近年發現的具有本征磁序的拓撲絕緣體MnBi2Te4及其系列材料, 兼備非平庸的拓撲性、二維的層狀材料結構、磁序來源非摻雜等優點, 克服了磁摻雜導致的磁帶隙不均勻性.同時, 盡管其磁有序溫度和磁摻雜拓撲絕緣體接近, 均約為20—30 K, 但由于其磁序主要來自于化學配比組分的過渡金屬元素(Mn), 它不僅能實現磁摻雜體系中大多數的物理效應, 而且其實現溫度普遍比摻雜體系高至少一個數量級, 因此吸引了非常廣泛的關注.

2.2.1 晶格結構

本征磁性拓撲絕緣體MnBi2Te4是一種A-BC型密堆垛層狀材料, 與本征/磁摻雜拓撲絕緣體不同的是, 它的結構基本單元是由V, VI族元素Bi和Te、過渡金屬元素Mn組成七原子層(septuple layer, SL)結構, 形成-VI-V-VI-TM-VI-V-VI-的截面堆垛, 其中過渡金屬元素位于SL的中心,如圖1(a)所示[44].SL層內原子間形成較強的共價鍵, 而層間VI-VI元素的結合方式則是范德瓦耳斯力相互作用主導.有趣的是, 通過對MnBi2Te4這類拓撲絕緣體進行晶格結構上的改造, 能形成新的磁序乃至拓撲序, 例如對Mn元素進行過渡金屬元素替換[45]或對Bi元素進行Sb替換/摻雜, 可衍生成一大類具有不同磁序的材料[44].另外, 如圖1(b)所示, 在SL之間插入若干層本征拓撲絕緣體Bi2Te3[46], 即從本征磁性拓撲絕緣體MnBi2Te4出發衍生出MnBi2nTe3n+1系列化合物或超晶格, 同時還取決于材料的厚度、插層結構、表面原子種類等, 也能對材料的磁有序、磁特性進行調控, 甚至形成新的拓撲相[19,46-49].

圖1 本征反鐵磁拓撲絕緣體MnBi2Te4的晶格結構、磁結構和電子結構 (a)晶格結構示意圖, 其中Mn原子的自旋如紅色箭頭所示, 材料呈A型反鐵磁序; (b)理論上不同厚度、磁化強度的MnBi2Te4 能實現的拓撲相; (c), (d)利用角分辨光電子能譜測量的表面能帶結構.圖(a)來自文獻[44], 圖(b)來自文獻[46], 圖(c)來自文獻[21], 圖(d)來自文獻[57]Fig.1.Crystalline, magnetic, and electronic structures of intrinsic antiferromagnetic topological insulator MnBi2Te4: (a) Schematic crystalline structure, the spins of Mn atoms are shown as red arrows, showing a type-A antiferromagnetic order; (b) topological phase diagram of MnBi2Te4 with different thicknesses and magnetizations; (c), (d) angle resolved photoemission spectroscopies of surface electronic structures.(a) is adopted from Ref.[44], (b) from Ref.[46], (c) from Ref.[21], and (d) from Ref.[57].

2.2.2 磁結構

根據理論計算和實驗研究表明[19,46-49], MnBi2Te4及其大多數的衍生化合物MnBi2nTe3n+1的磁結構均為A型反鐵磁序, 即在SL層內Mn是鐵磁性耦合, 而層間則是反鐵磁性耦合.通過調節插入本征拓撲絕緣體Bi2Te3的厚度, 能調節反鐵磁序的磁特性, 如磁翻轉磁場大小和反鐵磁層間的交換作用強度等[45], 從而改變實現反常霍爾效應、自旋翻轉等效應所需的磁場強度.近期的理論研究表明, 通過將Bi替換成Sb所形成的MnSb2Te4也具有反鐵磁序[50], 但實驗結果卻表明MnSb2Te4在25 K以下具有自發凈磁矩, 結合第一性原理計算證明它可能是亞鐵磁性的外爾半金屬[51,52], 但這與實驗結果有較大差異, 不同的樣品合成方法得到的磁有序不一致, 有報道稱是具有本征磁性的拓撲絕緣體, 是居里溫度為45—50 K的鐵磁性[53], 也可能是奈爾溫度約為19 K的反鐵磁性[54,55]等.近期X射線衍射和中子衍射的實驗揭示[51], 出現這種磁有序差異的可能原因是在所合成的MnSb2Te4中出現Mn和Sb原子的相互替代, 即形成反位無序(antisite disorder), 造成反鐵磁序和亞鐵磁序的共存, 相對于Mn原來所在的3a位置, Mn原子會在6c位置沿著c軸方向形成反平行的自旋結構,最終使Mn原子在一個晶胞中貢獻約2.1μB的磁矩(μB為玻爾磁子).在研究Mn(Bi,Sb)2Te4系列合金時進一步確認了這一結論, 且證實MnSb2Te4中的磁相互作用、局域的化學組分對磁有序影響非常大[53,55].

根據理論計算, 由于MnBi2Te4的A型反鐵磁序對拓撲性質可能存在一定的影響, 其拓撲性質會隨層數的奇偶性有一定的依賴關系[15].近期的反射磁圓二向色性譜研究了從單層到少層的MnBi2Te4在改變層數、溫度、外磁場等實驗條件的磁行為, 發現MnBi2Te4中自旋翻轉所需要的外磁場隨其SL層數變化存在一種有趣的奇偶效應[15], 進一步的理論計算表明其中主導的因素可能是材料表面自旋翻轉和體自旋翻轉的演化.隨著溫度升高,MnBi2Te4從反鐵磁序演變成順磁行為.可見,MnBi2Te4屬于一種弱反鐵磁體, 能通過一定大小的外磁場作用和特定溫度控制, 使不同層數的樣品具有不同的磁結構, 進而操縱該材料相關的量子效應.

2.2.3 電子結構

在低于奈爾溫度時, 雖然MnBi2Te4的反鐵磁序破壞了時間反演對稱性, 但由于Mn原子層在層內顯示出鐵磁耦合, 材料總體滿足時間反演T和空間平移τ1/2的聯合對稱性S=Tτ1/2, 體系存在Kramers簡并, 使得三維反鐵磁序的MnBi2Te4在拓撲上屬于二維拓撲不變量Z2分類[56].因此, 區別于本征拓撲絕緣體的時間反演對稱保護, 此本征反鐵磁拓撲絕緣體受到S聯合對稱性保護.有趣的是, 在S對稱性作用下, 材料只有在特定的、滿足S對稱性的晶面上才會具有拓撲保護的無帶隙表面態, 呈現線性狄拉克錐型色散; 而其他不滿足S對稱性的晶面上的表面態則被打開一個帶隙, 成為一種弱的拓撲絕緣體[56].根據這一特性可以通過選取材料的晶面或生長特定晶向的材料獲得相應的拓撲物性.

然而, 近期不同課題組使用不同的MnBi2Te4樣品進行角分辨光電子能譜研究, 各自得到的拓撲表面態結果存在較大分歧.如圖1(c)和圖1(d)所示, 近期的幾個實驗結果[57-59]表明, 在MnBi2Te4面上的拓撲表面態并沒有出現本該因反鐵磁序而打開的能隙, 反而觀察到無能隙狄拉克錐能帶; 相反, 在Bi2Te3表面上則出現了能隙, 這與早期的理論、實驗結果不一致[21].理論上, 一個可能的解釋是[57], 由于MnBi2Te4表面磁序與體磁序的不同,MnBi2Te4表面受到時間反演對稱性保護而顯示出無能隙; 而在Bi2Te3表面, 層間原子軌道的耦合作用導致磁性和雜化共同作用, 最后打開了能隙.另外, 準粒子干涉實驗發現, MnBi2Te4中電子的散射方向、色散關系與理論計算結果不一致[60], 同時實驗還發現能帶的自旋結構分布也受到層間能帶雜化的影響.當然, 可能的解釋也包括不同實驗組合成的樣品的質量有所不同, 因為MnBi2Te4材料自身的穩定性欠缺, 實驗結果更加值得深究.關于反鐵磁拓撲絕緣體MnBi2Te4的拓撲表面態電子結構的研究還需要進一步的實驗探索, 不過無論如何, MnBi2Te4表現出不同于傳統的本征、磁摻雜拓撲絕緣體中的體表對應關系, MnBi2Te4的表面態似乎不完全由其體態拓撲性質決定.

2.3 磁性外爾半金屬

除了拓撲絕緣體這一里程碑式的發現, 近年來領域還發現了以外爾半金屬(如TaAs[61])、狄拉克半金屬(如Na3Bi[62])等為代表的拓撲半金屬.在非磁性的外爾半金屬中, 時間反演對稱性的存在使得反常霍爾效應為零, 然而, 在磁性外爾半金屬中,非零的貝里曲率的存在, 會產生巨大的反常霍爾效應, 同時進一步的實驗表明磁性外爾半金屬的反常霍爾角也非常大, 因此磁性外爾半金屬能在自旋電子器件中有重要的潛在應用.然而, 理論上預測的幾種磁性外爾半金屬, 例如Re2Ir2O7(Re為稀土元素)[63-68], HgCr2Se4等在實驗上尚未觀察到理想的反常霍爾效應.對于Re2Ir2O7, 領域內目前認為在零磁場下仍不能確認這種磁性外爾半金屬的主要原因是, 外爾點能隨磁序參量而迅速演變, 配對最終會在布里淵區邊界湮滅, 造成電荷帶隙很容易被打開, 只在磁疇處剩下表面態的金屬部分[66].另外,即使在部分Re2Ir2O7(如Re= Nd, Pr)[66]中發現了非線性的霍爾效應, 且似乎與材料的外爾半金屬態[65]、能帶接觸點的半金屬態相關, 但非線性的霍爾效應同時也在具有all-in-all-out (AIAO)的自旋態和電荷帶隙[69]的材料(如Re= Eu,Y)[66,70-72]中發現, 因此其微觀的物理起源是由于內稟還是外稟因素(例如殘余應力[63]、Ir偏離了非磁性的離子態Ir3+而產生鐵磁性[72]等)仍然不清晰.對于HgCr2Se4, 有實驗觀察到了其半金屬特性, 且具有105 K的居里溫度, 成為支撐磁性外爾半金屬的重要實驗證據[73].然而, 輸運實驗上所得到的反常霍爾電阻率不僅較小[73,74], 大約在0.1 mΩ·cm量級, 還需要和普通霍爾效應進行分離和修正; 另外, 實驗還發現反常霍爾電阻和電導都與溫度T的1/2次方成線性正比, 并正比于樣品中的缺陷、無序, 揭示出其外稟的來源的可能性,即主要來源于費米面附近的散射[74].理論上可能需要對能帶貝里曲率中的本征項進行更深入的分析[7,75], 同時引進雜質散射的相對論模型, 考慮磁交換、自旋軌道效應、電子-電子相互作用等[76-78]才能徹底解釋這些實驗結果.上述的實驗結果與理論的偏離, 可能的原因還有這些材料的外爾點與費米能級距離較大, 或者由于拓撲平庸的費米面的載流子濃度非常高, 輸運實驗中難以測得外爾點導致的拓撲非平庸現象[79].這一問題直到近年才取得突破, 實驗上在一類Shandite化合物半金屬中觀察到巨大的反常霍爾電阻, 更重要的是在這材料體系中同時發現了磁性外爾半金屬存在的跡象, 因此這類化合物引起了廣泛的關注.相對于Re2Ir2O7和HgCr2Se4等磁性外爾半金屬的候選材料, 此類化合物的外爾點距離費米能級更近(如Co3Sn2S2只離費米能級約60 meV), 同時材料中的載流子濃度非常低, 因此材料的物性相對比較容易被外爾點所主導[79].經研究發現, 在這類材料中觀察到的反常霍爾效應主要來源于材料內的kagome層狀晶格結構所產生的特殊的磁性和拓撲特性.典型的例子是半金屬材料Co3Sn2S2, 它在Shandite體系中具有最高的磁有序溫度(175 K), 其鐵磁性主要來源于Co原子所構成的kagome層狀晶格, 它所形成的鐵磁性具有面外各向異性.近期的理論計算[22,79]顯示, 在Co3Sn2S2中, 一個自旋方向的通道在費米能級附近的能隙具有單自旋性質, 而另一個自旋方向的通道則出現能帶翻轉和線性交叉色散, 具有磁性外爾半金屬的關鍵特征, 近期的實驗也證實了Co3Sn2S2是磁性外爾半金屬[22].

另外, 近年引起廣泛關注的非共線反鐵磁材料Mn3Sn和Mn3Ge也被發現具有新穎的拓撲特性, 理論預測和現階段的實驗結果均表明它們也是磁性外爾半金屬.類似于Co3Sn2S2, 在Mn3Sn和Mn3Ge中, 過渡金屬Mn也形成了kagome晶格, 具有非共線反鐵磁結構, 其磁矩方向可以用大約幾百奧斯特的外磁場控制.另外, 理論計算和近期的實驗表明, 在Mn3Sn和Mn3Ge中存在與拓撲特性相關的巨反常霍爾效應、反常能斯特效應、自旋霍爾效應和自旋能斯特效應等豐富的物理效應.

2.3.1 晶格結構

如上文所述, Co3Sn2S2是Shandite化合物家族里一類具有kagome晶格的磁性外爾半金屬.Shandite 化合物具有的化學式(M為過渡族金屬,M′為主族金屬,X為VI族元素), 其中kagome晶格由過渡金屬元素所構成.因此, 沿著[0001]方向會有由不同元素占據的六方晶格, 如6個Sn原子、6個S原子、6個Co原子和1個Sn原子組成的kagome晶格, 其中Sn原子位于Co原子構成的kagome點陣中心, 形成S-Sn-Co3Sn的三明治結構, 即沿著[0001]方向為Sn-[S-(Co3Sn)-S]的準二維晶格結構, 如圖2(a)所示[22].

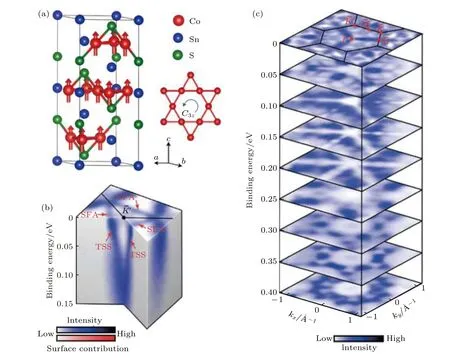
圖2 磁性外爾半金屬Co3Sn2S2的晶格結構、磁結構和電子結構 (a)晶格結構示意圖, 其中Co原子的自旋如紅色箭頭所示,材料呈鐵磁序; (b), (c)利用角分辨光電子能譜測量的能帶結構.圖(a)來自文獻[22], 圖(b)和圖(c)來自文獻[82]Fig.2.Crystalline, magnetic, and electronic structures of magnetic Weyl semimetal Co3Sn2S2: (a) Schematic crystalline structure,the spins of Co atoms are shown as red arrows, showing a ferromagnetic order; (b), (c) angle resolved photoemission spectroscopies of the electronic structures.(a) is adopted from Ref.[22], (b) and (c) from Ref.[82].

本綜述涉及的另一類具有kagome層狀晶格的磁性外爾半金屬Mn3X(X= Ge, Sn)二元合金,如圖3(a)所示[27], 這系列材料具有Ni3Sn型晶格結構, 屬于P63/mmc空間群, 其六邊形單元由兩層Mn沿著[0001]方向堆疊, 每一層中的Mn原子形成kagome晶格, 而X原子則在一個六邊形的中心, 形成如圖3(b)的六方準二維結構[27], 可以看作一個扭曲的、由正八面體組成的三角管結構.這個晶格結構只有在Mn過量的時候才能穩定, 一般情況下Mn會隨機占據Sn原子位置.

2.3.2 磁結構

Co3Sn2S2具有本征的垂直鐵磁序, 其磁性來自于Co原子所構成的kagome 晶格, 每個Co原子的磁矩強度為 0.3μB, 磁各向異性能約為0.6 meV[80].Co3Sn2S2的鐵磁性較強, 具有非常強的磁各向異性, 居里溫度約為175 K, 具有較大的磁矯頑力.由于kagome層間磁交換耦合強度是層內的一半左右, 因此, 總體上看它的磁序呈現準二維特征.而在Mn3X(X= Ge, Sn)中, 實際情況中有面內的輕微的扭曲, Mn原子在面內形成AIAO型的非共線反鐵磁結構, 如圖3(b)所示, 每個Mn原子磁矩約為 3μB.由于存在自旋阻挫, Mn3X晶格經常呈現具有很小的凈鐵磁矩(平均每個Mn原子貢獻約0.002μB)的倒三角自旋結構[27].

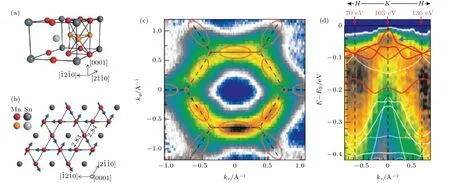
圖3 磁性外爾半金屬Mn3Sn的晶格結構、磁結構和電子結構 (a), (b)晶格結構示意圖, 其中Mn原子的自旋如藍色箭頭所示,材料呈反鐵磁序; (c), (d)利用角分辨光電子能譜測量的能帶結構.圖(a)和圖(b)來自文獻[27], 圖(c)和圖(d)來自文獻[84]Fig.3.Crystalline, magnetic, and electronic structures of magnetic Weyl semimetal Mn3Sn: (a), (b) Schematic crystalline structure,the spins of Co atoms are shown as blue arrows, showing an antiferromagnetic order; (c), (d) angle resolved photoemission spectroscopies of the electronic structures.(a) and (b) are adopted from Ref.[27], (c) and (d) from Ref.[84].

2.3.3 電子結構

在能帶結構中, 外爾半金屬具有優異的拓撲特性, 主要來源是電子體能帶結構中的外爾節點, 而這種節點一般由于破缺空間翻轉對稱性或時間反演對稱性所形成, 具有明確的手性, 并且與費米弧表面能帶有關.費米弧從一個外爾節點出發, 在表面二維動量空間內以相反的手性終止于另一個外爾節點, 即一種不連續的費米面結構[81].因此,體態上外爾節點的存在保證了費米弧的形成.如圖2(b)和圖2(c)所示, Co3Sn2S2在費米能級附近有三條因能帶交叉而產生的節線環, 以及由于強自旋軌道耦合打開而產生的三對外爾節點, 這一預測的能帶結構在近期實驗上成功被觀察到[82].同期的實驗[24]觀察到了由Co原子構成的kagome晶格, 并通過分析電子在不同原子終端面發生彈性散射時的準粒子干涉花樣, 獲得了不同的表面態費米弧的色散關系.研究發現[24]在Sn, Co, S三個不同的終端面上施加不同表面電位, 可以修改費米弧的輪廓和外爾點的連通性.在Sn終端面上能觀察到布里淵區內外爾點的費米弧連通性, 而在Co面上,這種連通性會跨越相鄰的布里淵區域, 在S面上,費米弧會與拓撲平庸的體態和表面狀態發生交疊.此實驗結果同時驗證了外爾半金屬Co3Sn2S2中的拓撲保護和非拓撲保護的電子特性, 確立了其體態-表面態之間的關聯.

外爾半金屬既可以是非磁性的、鐵磁性的, 也可以是反鐵磁性的, 只要其空間翻轉稱性(P)和時間反演對稱性(T)組成的PT對稱性被破缺.在磁性外爾半金屬Mn3X中存在非共線反鐵磁自旋結構, 其中的反鐵磁交換耦合和Dzyaloshinskii-Moriya 相互作用, 由于破缺了時間反演對稱性T,因此也破缺了PT對稱性, 從而允許能帶中出現外爾點[83].當不考慮材料中的自旋軌道耦合時,Mn3X的能帶結構中低能量附近會形成圍繞K點的節點環; 當考慮自旋軌道耦合后, 該節點環會演化成K點附近的多對外爾點, 因此一般情況下強自旋軌道耦合是形成外爾半金屬的必要條件.另外, 磁性外爾半金屬的一個典型能帶特點是某個自旋方向通道在費米能級附近是具有帶隙的, 但在另一個自旋通道中則為有強的能帶翻轉和線性交叉.近期利用角分辨光電子能譜[84]觀察了Mn3Sn的電子結構, 如圖3(c)和圖3(d)所示, 與上述理論預測基本相符.

2.4 磁性狄拉克半金屬

3d過渡金屬的kagome層狀晶格是研究在關聯拓撲相中具有對稱性保護的電子態的理想平臺,能容納不同類型的量子磁態.如上文所述, 在近期發現的磁性外爾半金屬中, kagome晶格對拓撲相的形成起了非常重要的作用.除了磁性外爾半金屬, kagome晶格也能成為磁性狄拉克半金屬的材料母體, 近期理論和實驗都研究表明, 有一系列具有kagome晶格的層狀磁性材料具有狄拉克電子的能帶結構或電子特性, 是狄拉克半金屬的重要候選材料.盡管磁性外爾半金屬、磁性狄拉克半金屬的形成并非一定需要kagome晶格, 但具有kagome晶格的磁體與拓撲材料確實具有相當大的重疊部分, 研究具有kagome晶格的磁性材料對尋找新型拓撲材料具有重要的探索意義.這一節將主要討論兩種具有kagome層狀晶格的磁性狄拉克半金屬—Fe3Sn2, FeSn.

2.4.1 晶格結構

在部分具有kagome晶格的二元金屬間化合物TmXn(T= Mn, Fe, Co等過渡金屬;X= Sn,Ge;m∶n= 3∶1, 3∶2, 1∶1)中, 不同的kagome層、間隔層的堆垛方式能導致不同的準二維電子結構和磁結構, 往往會因此而導致不同的拓撲特性, 此類磁體也稱為kagome磁體.除了上文所述的磁性外爾半金屬Mn3X(X= Ge, Sn)以外, 近期發現此類化合物的代表—Fe3Sn2, FeSn, CoSn, 同樣具有kagome層狀晶格[14,31,85-87], 在存在鐵磁序的條件下能承載有質量的狄拉克費米子態, 是磁性狄拉克半金屬的重要候選材料.對于TmXn系列材料,其kagome晶格由3d過渡金屬(T= Mn, Fe, Co)組成, kagome晶格中心則由IV族原子X(X=Sn, Ge)填充, 間隔層由X原子組成, 形成六方晶格.這些kagome晶格在面內都有不同的平移, 并且由不同的kagome層 (記為A/B)與間隔層(記為S)進行堆垛[14], 如AB, ABSBCSCAS, ASA,隨著X∶T比例的增加, 材料會更顯二維性.對于本節介紹的Fe3Sn2, 如圖4(a)所示[85], 它具有雙層kagome結構, 空間點群屬, 可以看作是一層錫烯被兩層Fe3Sn夾著.由于這些層之間的結合力較弱, Fe3Sn2樣品很容易被解理出FeSn或Sn終止面.而FeSn的晶格結構相對Fe3Sn2和Mn3X都要簡單, FeSn中每個晶胞中只存在一個kagome層, 如圖5(a)所示[88], 其中的kagome層與層之間距離較大, 是此類化合物中最接近二維極限的磁性狄拉克半金屬.

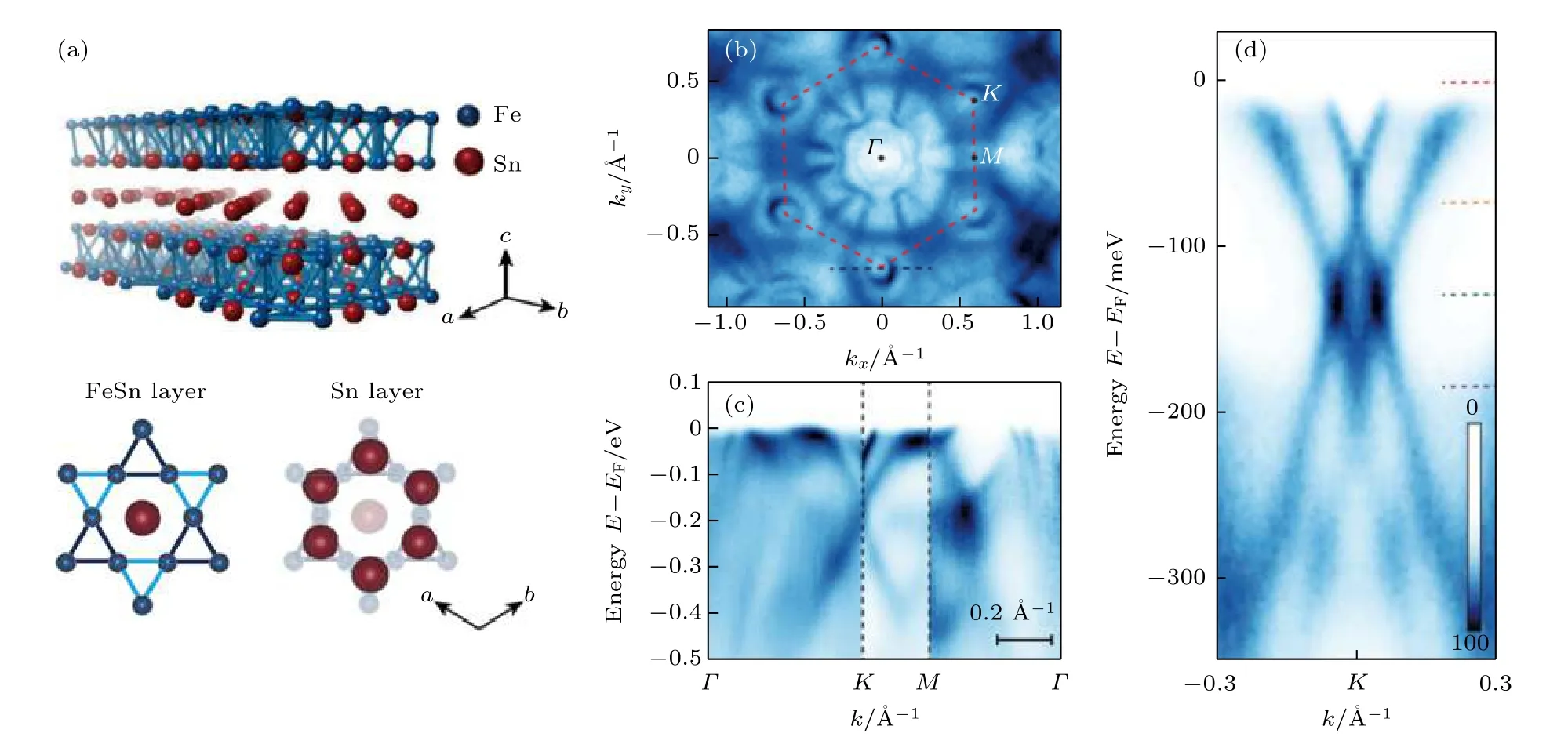
圖4 磁性外爾半金屬Fe3Sn的晶格結構和電子結構 (a)晶格結構示意圖; (b)—(d)利用角分辨光電子能譜測量的能帶結構.圖(a)來自文獻[85], 圖(b)—(d)來自文獻[31]Fig.4.Crystalline and electronic structures of magnetic Weyl semimetal Fe3Sn: (a) Schematic crystalline structure; (b)—(d) angle resolved photoemission spectroscopies of the electronic structures.(a) is adopted from Ref.[85], (b)—(d) from Ref.[31].

圖5 磁性外爾半金屬FeSn的晶格結構、磁結構和電子結構 (a)晶格結構示意圖, 其中Fe原子的自旋如紅、藍色箭頭所示, 材料呈反鐵磁序; (b), (c)利用角分辨光電子能譜測量的能帶結構.圖(a)來自文獻[88], 圖(b)和圖(c)來自文獻[14]Fig.5.Crystalline, magnetic, and electronic structures of magnetic Weyl semimetal FeSn: (a) Schematic crystalline structure, the spins of Fe atoms are shown as red and blue arrows, showing an antiferromagnetic order; (b), (c) angle resolved photoemission spectroscopies of the electronic structures.(a) is adopted from Ref.[88], (b) and (c) from Ref.[14].

2.4.2 磁結構

早期的實驗研究[89]表明Fe3Sn2是一種不尋常的磁性導體, 居里溫度高達670 K, 其飽和磁場和飽和磁化強度與溫度依賴關系不明顯, 在低溫下的飽和磁化強度約為每個Fe原子1.9μB, 是一種軟磁體[31].另外有研究指出[13], Fe3Sn2中的這種高溫鐵磁序可能是與電子關聯和kagome晶格的協同作用有關.由于Fe3Sn2中存在kagome平帶, 這種平帶具有較高態密度和較大的在位庫侖能, 這使得Fe3Sn2鐵磁序的Stoner判據得以滿足[13].從實空間看, 這種電子間較強的在位庫侖相互作用會使束縛在六角形晶格內的電子自旋極化, 同時, 分子間磁交換作用能產生局域極化自旋磁矩, 這兩種效應共同通過共享Fe原子的六角形網格發生耦合, 從而導致長程鐵磁序.最近, 類似的平帶也在CoSn中發現[87].而m∶n= 1∶1的FeSn則為一種反鐵磁體, 在每個kagome晶格內, Fe原子發生鐵磁性耦合, 而沿著c軸的kagome晶格則為反鐵磁性耦合.FeSn還可以看作是一系列的Fe3Sn kagome晶格的堆垛, 早期的中子衍射實驗[90]證明每個Fe3Sn kagome晶格的磁化方向平行于 [3.732,1, 0]方向.

2.4.3 電子結構

如圖4(b)—(d)所示, 利用角分辨光電子能譜對Fe3Sn2進行觀察, 可以看到, 在布里淵區的K和K′附近存在一對準二維狄拉克錐[31].這一對狄拉克錐的中心在K點, 并且有能量上的區分, 如圖4(d)所示.另外, 結合掃描隧道顯微術、角分辨光電子能譜、第一性原理計算等手段發現, Fe3Sn2還存在平帶電子結構[13].這與狄拉克錐型的能帶形成鮮明對比, 由于狄拉克錐能帶中電子的等效質量為零, 而平帶中的電子具有很大的質量, 這兩種極端的能帶結構同時存在于Fe3Sn2中.經研究, 影響能帶平坦程度的主要因素是kagome晶格內布洛赫波函數的局部破壞程度, 在Fe原子所形成的kagome晶格中, 電子布洛赫波函數的相消干涉能夠有效地將電子束縛在kagome晶格的六角形單元中, 從而導致幾近無色散的平帶.在結構相對簡單的FeSn中, 由于反鐵磁kagome結構破缺了每層的空間翻轉對稱性P和時間反演對稱性T, 但服從PT聯合對稱性, 是實現無質量狄拉克費米子的理想平臺.近期在FeSn的角分辨光電子能譜實驗和輸運實驗中同時觀察到狄拉克電子結構(圖5(b)和圖5(c))、平帶以及de Haas-van Alphen量子振蕩, 表明FeSn中共存表面態和體態的狄拉克電子[14,88].通過理論計算發現, 體狄拉克能帶主要來源于局域化的Fe-3d軌道, 而狄拉克表面態表現出完全的二維自旋極化和自旋軌道鎖定特性.

3 二維磁性拓撲材料的物理效應

3.1 本征磁性拓撲絕緣體

如上文所述, MnBi2Te4具有層間反鐵磁排布,其宏觀磁性乃至拓撲性質會隨著層數的奇偶性發生變化.理論上, 當MnBi2Te4具有偶數層時, 層間磁矩正好互相抵消, 宏觀磁矩為零.雖然該體系從能帶拓撲不變量而言應屬于弱拓撲分類, 但是從拓撲場角度而言則能滿足靜態軸子絕緣體的實現條件, 即軸子場等于π, 本征反鐵磁性能使拓撲表面態打開能隙, 是一種天然的軸子絕緣體, 并能產生奇特的拓撲磁電響應.當MnBi2Te4的層數為奇數時, 體系存在未被抵消的凈磁矩, 當材料厚度大于一定值時, 材料的上下表面之間的耦合可以忽略,原則上能實現量子反常霍爾效應, 即形成陳絕緣體.然而, 現實材料遠不如理論中的模型簡單, 下面將從近期針對MnBi2Te4的實驗結果, 總結理論、實驗發現的重要物理現象.

3.1.1 量子反常霍爾效應

量子反常霍爾效應自從在磁摻雜拓撲絕緣體中發現后一直是凝聚態物理領域的前沿熱點之一.然而, 摻雜原子的隨機性、不均勻性不僅使得所產生的鐵磁序欠缺穩定性和均勻性, 還會引入一定的帶隙內雜質態、缺陷態, 這使得費米能級的展寬收窄需要極低溫條件, 并且不與帶隙內的雜質態、缺陷態接觸, 才能實現霍爾電導的完全量子化、相應磁阻的極小化.目前, 在磁摻雜體系中, 這一極低溫普遍需要500 mK或更低, 盡管能通過材料結構的優化[91]使磁摻雜拓撲絕緣體實現霍爾電阻量子化的溫度提高到1 K左右, 但其磁阻仍需要更低的溫度才能進一步降低, 實現無耗散輸運.為了解決極低溫這一問題, 近年來領域一直尋找一種非磁摻雜、具有本征磁序的拓撲絕緣體, 期望能從根本上解決磁摻雜的不均勻問題, 將量子反常霍爾效應的實現溫度大幅度提高.

直至近年, 一個相對比較理想的磁性拓撲絕緣體被理論預測、實驗證實, 即上文提到的具有本征反鐵磁序的拓撲絕緣體MnBi2Te4, 材料中的磁性主要來源于Mn, 而Mn具有確定化學計量比和確定的原子晶格位置并且有序排列, 材料的奈爾溫度在24 K左右.通過角分辨光電子能譜測量發現[16],當MnBi2Te4的厚度不小于兩個SLs時, 就能觀察到具有狄拉克錐型的表面態, 證明它是一個三維拓撲絕緣體.根據理論計算, 當MnBi2Te4的層厚為奇數且上下表面雜化可忽略時, 材料呈現量子反常霍爾效應, 層厚為偶數時則處于軸子絕緣體相, 并呈現拓撲磁電效應.有待實驗證明的是, 這種具有拓撲軸子表面態的反鐵磁拓撲絕緣體的三維體相在外加磁場下能否轉變為磁性外爾半金屬.這種外爾半金屬的電子結構非常簡單, 只有一對外爾點,是拓撲物理平臺理想的研究對象.MnBi2Te4的磁交換帶隙約有50 meV, 而磁摻雜拓撲絕緣體的交換帶隙寬度從幾個meV到幾十個meV起伏(取決于其均勻性), 相對而言MnBi2Te4的帶隙更穩定、均勻, 有望在更高溫度下實現量子反常霍爾效應[45].直到2020年, 實驗上在1.4 K的溫度下, 在5SLs厚的MnBi2Te4樣品中觀察到零磁場量子反常霍爾效應[20](圖6(a)和圖6(b)).有趣的是, 在實現量子反常霍爾效應的樣品中調節適當的載流子濃度后, 在高磁場下還能進一步觀測到常規的量子霍爾效應.假如把實現量子反常霍爾效應的零磁場條件放寬, 對樣品施加一個強磁場使得樣品的反鐵磁結構轉變成鐵磁結構, 能進一步將量子反常霍爾效應的實現溫度提高到6.5 K.這一工作成功地證明了MnBi2Te4是一個能實現量子反常霍爾效應的本征反鐵磁拓撲絕緣體.最近的實驗表明[92],高溫量子反常霍爾效應不僅能在MnBi2Te4中實現, 還能在MnBi2Te4系列材料中形成, 如1SLMnBi2Te4/4QL-Bi2Te3超晶格, 當把費米能級調控到表面帶隙內時, 霍爾電導也量子化到e2/h(e為電子電荷,h為普朗克常數).然而, 目前只有將MnBi2Te4塊材解理所得的Mn-Bi-Te薄膜才能實現量子反常霍爾效應, 還沒有直接生長的外延膜可以實現這一效應, 可能的原因是材料的穩定性欠缺和費米能級的位置偏離等, 近期研究發現在MnBi2Te4摻雜Sb能有效調節其費米能級的位置, 這使Mn(Bi, Sb)2Te4成為一種能通過優化材料成分、外延生長實現量子反常霍爾效應的候選材料[44].

圖6 本征磁性拓撲絕緣體的量子反常霍爾效應、軸子絕緣體態 (a)霍爾電阻; (b)磁阻; (c)零磁場下縱向電阻率的柵極電壓調制; (d)磁場和柵極電壓調制下的相圖.圖(a)和圖(b)來自文獻[20], 圖(c)和圖(d)來自文獻[18]Fig.6.Quantum anomalous Hall effect and axion insulating state in the intrinsic antiferromagnetic topological insulator: (a) Hall resistance; (b) magneto-resistance; (c) gate-bias modulated longitudinal resistivity under zero magnetic field; (d) a phase diagram of magnetic field and gate bias.(a) and (b) are adopted from Ref.[20], (c) and (d) from Ref.[18].

3.1.2 軸子絕緣體態

理論上在磁性拓撲絕緣體薄膜中, 當兩個表面的磁化方向相同時, 兩個表面分別貢獻的霍爾電導為e2/(2h) , 總的霍爾電導則為二者之和, 即e2/h,為量子反常霍爾效應的霍爾電導; 當磁化方向相反時, 兩個表面的霍爾電導符合相反, 總的霍爾電導正好抵消為零, 這一狀態理論上為靜態軸子絕緣體態.如果在MnBi2Te4中選擇S聯合對稱性被破缺的晶面, 則其拓撲表面態會被打開能隙, 同時材料的厚度足夠讓表面雜化可以忽略, 消除有限尺寸效應, 得益于自身的A型反鐵磁序, 正好能滿足表面磁化方向相反的條件, 此時的MnBi2Te4就能實現靜態軸子絕緣體態[21,45], 其軸子場θ=π.最近的實驗[18]成功在MnBi2Te4體系中實現了陳絕緣體和軸子絕緣體這兩種拓撲量子態, 并觀察到二者之間的拓撲相變.如圖6(c)所示, 在6SLs厚的MnBi2Te4中跟蹤其縱向電阻、霍爾電阻對費米面位置的依賴關系時發現, 當費米面被移至表面帶隙內, 材料進入拓撲非平庸區間.此時, 在低磁場下, 樣品的縱向電阻高達6h/e2, 進入一個絕緣態, 此時的霍爾電阻為零, 這樣的輸運特性能維持在—3—3 T的磁場區間, 是軸子絕緣體態存在的重要證據.隨著磁場繼續增加, MnBi2Te4中Mn的反平行自旋被轉變為平行自旋的狀態, 此時縱向電阻迅速減小至接近零, 而霍爾電阻則增加至量子化的h/e2, 體系進入到量子反常霍爾絕緣體態, 如圖6(d)所示.這一拓撲相變的輸運實驗表明MnBi2Te4是一個實現、研究量子反常霍爾效應、軸子絕緣體態的綜合平臺.然而, 這些對軸子絕緣體態的實驗觀察, 即零霍爾電阻、高縱向電阻, 未能完全排除平庸絕緣體的可能性[93], 為了進一步證明量子態的拓撲性, 觀察到拓撲磁電效應, 即電場誘導磁極化, 磁場誘導電極化, 仍需要進一步的實驗證實.

3.1.3 其他拓撲相和拓撲相變

雖然理論上已經預測在MnBi2Te4中能實現量子反常霍爾效應、軸子絕緣體態, 而目前要制備能實現這兩個效應的MnBi2Te4材料仍頗具挑戰,很多實驗結果都未能達到量子化的結果[17,19,47], 或需要不同的超晶格結構, 或很高的磁場來使材料變成鐵磁態等, 這使對MnBi2Te4的實驗研究、物理圖像的理解受阻, 因此, 從理論上理解這些實驗結果非常具有指導意義.對于Mn-Bi-Te系列材料(如MnBi2Te4, MnBi4Te7)[19], 2019年, Sun等[46]通過利用有效模型和第一性原理計算發現, 二維多層的Mn-Bi-Te材料能實現多種拓撲相, 不僅僅是量子反常霍爾絕緣體、軸子絕緣體, 實際的實驗結果可能還會包括一些其他的量子態或拓撲相, 如時間反演對稱的量子自旋霍爾效應、時間反演破缺的量子自旋霍爾效應等.圖1(b)總結了本征拓撲絕緣體Bi2Te3以及磁性拓撲絕緣體Mn-Bi-Te系列的二維結構在磁交換場下的相圖, 其中可調參量是層厚和磁交換場強度[46].

盡管理論計算表明, 當MnBi2Te4的層數為奇數時, 材料處于量子反常霍爾絕緣相, 偶數層時處于軸子絕緣體相, 但近期的實驗[94]發現, 在測量厚度為9SLs和10SLs的器件中, 在外加約5 T的垂直磁場下, 樣品的霍爾電阻量子化到半個量子電阻(h/(2e2) ), 出現半量子化霍爾電阻平臺, 而對應的縱向電阻趨近于零.這一實驗結果表明樣品可能進入一個特殊的、陳數為2的拓撲態.在理論上的理解, 這種高陳數量子態可能意味著, 當MnBi2Te4滿足特定條件時能實現磁性外爾半金屬態[45].

另外, 通過Bi2Te3插層所形成的MnBi2nTe3n+1(這里取n= 2, 3為例)系列材料, 即MnBi4Te7,MnBi6Te10, 近期的理論計算和實驗結果發現這類材料在低溫下與MnBi2Te4類似, 均顯示A型反鐵磁, 只是隨著n的增大(Bi2Te3插層的增加), 層間反鐵磁耦合強度會變弱, 使得鐵磁序的飽和磁場降低[19], 約1.6 kOe的垂直磁場即可發生自旋翻轉[49], 奈爾溫度也從MnBi4Te7的13 K過渡至MnBi6Te10的11 K, 而MnBi6Te10幾乎顯示出極化的鐵磁序[95].同時, 在MnBi4Te7中通過沿著[00L]方向的布拉格反射實驗探測到一個面內0.15μB/Mn的磁矩[49].近期的角分辨光電子能譜對MnBi4Te7的研究顯示, 它也是一個拓撲分類為Z2拓撲不變量的反鐵磁拓撲絕緣體, 并且根據不同終止面(MnBi4Te7終止面和Bi2Te3終止面)具有兩種不同的表面態[19].對于MnBi6Te10,近期的實驗表明它也是一種反鐵磁拓撲絕緣體,當在0.1 T外磁場作用下材料發生自旋極化, 此時會形成一個拓撲數為Z4= 2的鐵磁性軸子絕緣體[96], 并觀察到一個飽和的反常霍爾效應[97].有趣的是, 在MnBi6Te10中有三種不同的終止面, 分別為BBA, BAB, ABB (A代表MnBi4Te7, B代表Bi2Te3)型, 而在這三種終止面上能觀察到三種不同的狄拉克表面態.

3.2 磁性外爾半金屬

與狄拉克費米子類似, 外爾費米子可以看作動量空間的貝里曲率通量的磁單極子, 自然會對空間中電子的運動造成影響, 一個直接的結果就是導致內稟反常霍爾效應, 以及非零貝里曲率導致的其他物理效應等, 如手性異常、反常能斯特效應.通常情況下, 當在磁性外爾半金屬中實現內稟反常霍爾效應時, 其反常霍爾電導會正比于一對手性相反的外爾費米子在動量空間的間距, 并受到外爾費米子離費米能級的距離的影響.下面將介紹在磁性外爾半金屬中發現的重要物理效應, 典型的包括巨反常霍爾效應、手性異常、拓撲增強反常能斯特效應這三種與外爾點的存在有關的量子效應, 展現出磁與拓撲相互作用下豐富的物理現象.

3.2.1 巨反常霍爾效應

在磁性外爾半金屬中, 外爾節點和節線環都可能產生拓撲增強的貝里曲率, 從而在實驗上觀察到內稟反常霍爾效應的增強.這一效應的大小往往取決于費米能級位置的電子占據態以及附近的能帶結構.盡管這一預測在已提出的幾種磁性外爾半金屬(如Re2Ir2O7, HgCr2Se4, Co基Heusler 化合物等)[98-100]中均未能觀察到, 近期實驗上首先在磁性外爾半金屬Co3Sn2S2觀察到了巨大的內稟反常霍爾電導和巨反常霍爾角, 以及關于外爾費米子導致的奇異輸運行為[22,23].由于Co3Sn2S2的居里溫度約為175 K, 在低于這一溫度的范圍, 如150 K,實驗上觀察到了約1130 Ω—1·cm—1的大反常霍爾電導, 并且這一反常霍爾電導對溫度的依賴關系并不明顯, 如圖7(a)所示.這一結果顯示Co3Sn2S2的反常霍爾電導可能主要由非零貝里曲率貢獻, 這一曲率對溫度不敏感導致所測量的反常霍爾電導在寬溫度區間內保持相對較大且穩定的值[22].Co3Sn2S2樣品的載流子濃度低, 這使得Co3Sn2S2具有一個約20%的巨反常霍爾角.此反常霍爾電導和反常霍爾角比常規磁性材料至少高出一個數量級.同時, Co3Sn2S2的正磁阻似乎隨著磁場增加沒有呈現飽和的趨勢, 具有補償型半金屬的特征.進一步的實驗表明[101], 通過在Co3Sn2S2中摻雜Ni, 即Co3—xNixSn2S2, 觀察到異常增強的反常霍爾電導,觀測值約為1380 S/cm.通過分離反常霍爾效應的內外稟貢獻發現, 內稟反常霍爾電導為1340 S/cm,因此這種異常增強的反常霍爾電導幾乎完全來自于內稟貢獻.另外, 反常霍爾角和反常霍爾因子同時獲得增強, 最大值分別達到22%和2.3 V—1.在Co3Sn2S2中摻雜Ni主要表現為多電子摻雜, 這樣的增強現象無法基于剛帶模型理解, 目前將這一增強效應歸咎于無序的摻雜對貝里曲率產生的影響.

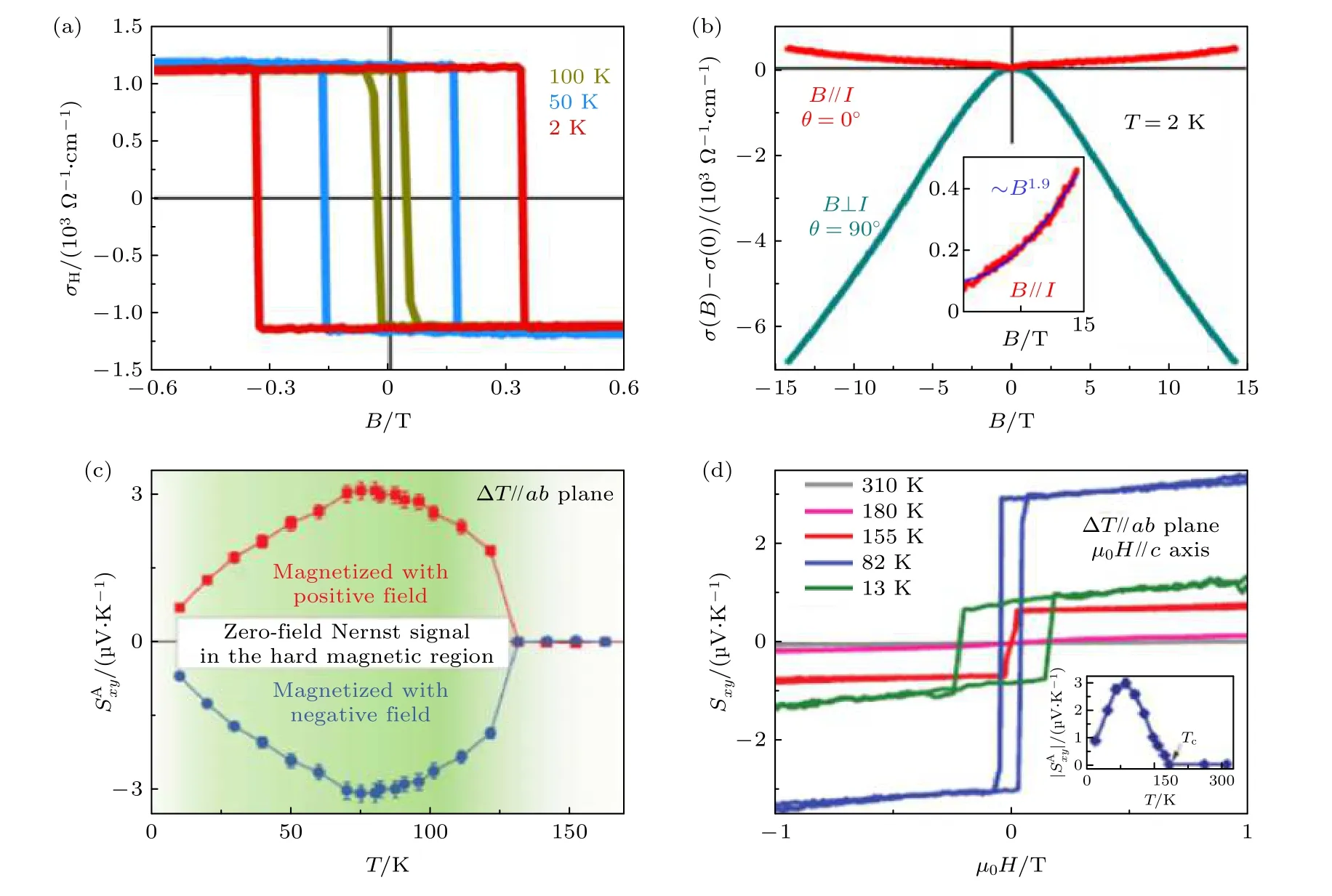
圖7 磁性外爾半金屬Co3Sn2S2的反常霍爾效應、手性異常和反常能斯特效應 (a)霍爾電導; (b)磁電導; (c), (d)反常能斯特熱功率.圖(a)和圖(b)來自文獻[22], 圖(c)和圖(d)來自文獻[109]Fig.7.Giant anomalous Hall effect, chiral anomaly, and anomalous Nernst effect in magnetic Weyl semimetal Co3Sn2S2: (a) Hall conductance; (b) magneto-electric conductance; (c), (d) anomalous Nernst thermal power.(a) and (b) are adopted from Ref.[22],(c) and (d) from Ref.[109].

對于另一類磁性外爾半金屬Mn3X(X= Ge,Sn), 其磁序為反鐵磁, 幾乎沒有凈磁矩.對比于鐵磁性材料的反常霍爾效應而言, 理論上Mn3X應該不會表現出反常霍爾效應.而實驗上, Mn3X這種非線性三角反鐵磁性卻也觀察到很大的反常霍爾效應[27-29,102].如上文所述, 這源于材料中的手性自旋結構所產生的非零貝里曲率, 且這一反常霍爾效應的主要貢獻來源于內稟電子結構, 同時這一來源導致的反常霍爾電導比外稟(凈磁矩)因素導致的反常霍爾效應更大.以Mn3Ge為例[29], 圖8(a)顯示了Mn3Ge在第一布里淵區的反常霍爾電導分布, 其中在ki-kj平面內的反常霍爾電導張量對應于所有占據電子態的貝里曲率在k方向上的積分, 在xy和yz上的分量均接近零, 僅在xz方向上具有很大的值約為330 (Ω·cm)—1.這一結果主要是因為Mn3Ge晶格內存在關于xz平面的鏡面對稱性(圖8(b)),關于這一鏡面反平行且可以通過這一鏡面反射互相轉換.為了證明Mn3Ge中大的反常霍爾效應來源于非線性反磁鐵自旋結構, Nayak等[29]實驗上通過調整磁場方向, 使其平行于不同晶體方向的情況下, 對樣品的磁化強度進行了系統的研究.當磁場平行于晶面時, 測量得到的磁化非常微小, 僅有約0.005μB/Mn; 當磁場平行于晶面時, 幅值只稍有增大.這一結果在不同溫度下, 如300和2 K,測得的磁化強度變化不大.雖然Mn的磁矩一般認為只在面內, 實驗發現當磁場平行于[0001]方向時仍能測量到非常小的磁矩0.0007μB/Mn, 這表明可能Mn的自旋磁矩在c軸方向上有很小的傾斜.因此, Mn3Ge樣品的磁矩非常接近零, 具有相對理想的反鐵磁序.進一步的角度依賴測量總結出這些極小的面內殘余磁矩對反常霍爾效應沒有重要的貢獻.因此, 結合這些實驗結果可以得知, 在Mn3Ge中測量到的巨反常霍爾效應主要源于其非線性反鐵磁自旋結構.

3.2.2 手性異常

在外爾半金屬中, 當所加的電流與外加磁場方向平行時, 外爾費米子所在的能帶會被朗道能級化, 這一量子化現象會導致手性電荷不守恒, 電荷因此在兩個手性相反的外爾節點之間流動, 在宏觀實驗上表現為負的磁電阻行為.在對Co3Sn2S2的轉角輸運測量中發現[22], 當所加的電場與外磁場垂直時, 縱向電阻為正值, 而外加磁場在面內方向時, 縱向電阻則轉變為負值, 如圖7(b)所示.這一輸運現象被初步認定為外爾費米子導致的手性異常.

除了在Co3Sn2S2中觀察到上述手性異常的實驗現象, Kuroda等[84]也在另一種磁性外爾半金屬Mn3Sn中觀察到類似的現象.為了讓手性異常在磁電輸運中占主導貢獻, 實驗上合成了一個Mn含量稍高的樣品Mn3.06Sn0.94, 這使得費米能級與外爾點之間的距離進一步縮小至約5 meV.研究發現, 當電流方向沿著方向時, 即外磁場分別平行和垂直于所加的電流方向, 如圖8(d)所示, 樣品的磁電導在60 K顯示出非常強的各向異性, 當外磁場平行(垂直)于電流時, 縱向電導隨著磁場的增加而增加(減少), 這一現象與在300 K下的實驗結果一致.重要的是, 當外磁場平行于電流時, 樣品顯示出來的磁電導不隨著磁場的增加而飽和, 在所測量的磁場范圍(9 T)還沒有顯示出飽和的跡象.這與Co3Sn2S2的輸運實驗結果一致, 僅當所加的電場和磁場相互平行時才會出現正的磁電導(負磁阻)現象, 因此也表明在Mn3Sn中觀察到手性異常.

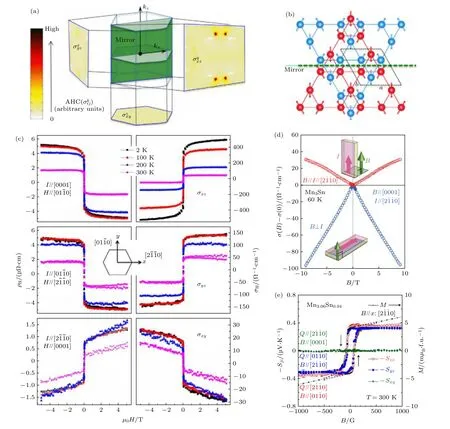
圖8 磁性外爾半金屬Mn3Ge的反常霍爾效應、Mn3Sn的手性異常和反常能斯特效應 (a)動量空間中Mn3Ge的反常霍爾電導分布; (b)在Mn3Ge中自旋結構的鏡面對稱性; (c) Mn3Ge的霍爾電阻率; (d) Mn3Sn的面內外的縱向電導; (e) Mn3.06Sn0.94的反常能斯特熱功率.圖(a)—(c)來自文獻[29], 圖(d)來自文獻[84], 圖(e)來自文獻[111]Fig.8.Anomalous Hall effect in magnetic Weyl semimetal Mn3Ge, chiral anomalyand anomalous Nernst effect in magnetic Weyl semimetal Mn3Sn: (a) Distribution of anomalous Hall conductance of Mn3Ge in momentum space: (b) spin texture with mirror symmetry in Mn3Ge; (c) Hall resistivity of Mn3Ge; (d) longitudinal conductance of both in- and out-plane for Mn3Sn; (e) anomalous Nernst power of Mn3.06Sn0.94.(a)—(c) are adopted from Ref.[29], (d) from Ref.[84], (e) from Ref.[111].

目前為止, 當外加磁場、電場同時在面內方向時出現的負的縱向磁阻效應被視為手性異常存在的重要證據, 但是最近的理論和實驗均指出[103-106],其他機制也可以誘導出負的縱向磁阻, 例如中性/離子雜質導致的軸異常、電流分布的不均勻性、電導漲落等.另外, 對于沒有手性異常的拓撲絕緣體,在實驗上也能夠觀測到負的縱向磁阻[107,108].因此,負的縱向磁阻不能簡單地視為手性異常存在的確切證據.手性異常的物理特征還待進一步的理論、實驗研究.

3.2.3 拓撲增強的反常能斯特橫向熱電效應

與內稟反常霍爾效應類似, 內稟反常能斯特效應也主要受到費米能級附近的電子填充態及貝里曲率分布的影響.近期對磁性外爾半金屬Co3Sn2S2的熱輸運研究中發現存在拓撲增強的反常能斯特效應[109].實驗上, Co3Sn2S2在薄膜形式下由于與襯底之間的作用、應力等因素, 其矯頑力顯著增強,高達5 T, 可以使體系保持硬磁單疇狀態, 無需施加外磁場即可持續產生能斯特效應.如圖7(c)和圖7(d)所示, 在80 K、零外加磁場的實驗環境下測得的Co3Sn2S2的橫向塞貝克系數約為3 μV/K,但這一值遠高于由于其飽和磁矩(僅為0.9μB/f.u.,f.u.指formula unit標準單位)所能產生的能斯特熱功率.結合電輸運結果和密度泛函計算得知, 這一巨大的反常能斯特效應可能主要來源于其電子結構中的結點線和外爾點所引起的強貝里曲率, 即主要來源于其內稟貢獻, 而材料本身的凈磁矩可能只貢獻很少的一部分反常能斯特信號, 即外稟貢獻.這一研究結果為提高材料的能斯特效應提供了重要的啟示, 也為尋找高能斯特熱功率的材料提供實驗指引.

理論上, 反常能斯特效應能提供一種在費米能級附近對貝里曲率的有效探測方案[75,110], 尤其是對于零磁矩的磁性材料(如反鐵磁體).在近期的實驗中, 類似的巨反常能斯特效應也在反鐵磁性外爾半金屬Mn3X(X= Ge, Sn)中發現[111-113].如在Mn含量略高的Mn3.06Sn0.94中, 盡管每個Mn原子磁化強度大約只有0.002μB, 在室溫和零磁場下,該材料顯示出來的橫向塞貝克系數高達0.35 μV/K,而在200 K溫度下, 這一數值能進一步提升到0.6 μV/K, 與目前鐵磁性金屬中最高的塞貝克系數可比擬(圖8(e))[111].通過第一性原理計算表明,這一巨大的能斯特效應主要來源于在費米能級附近的外爾點處強大的貝里曲率.這一結果表明類似于上文的鐵磁性外爾半金屬Co3Sn2S2的結論, 不管材料的磁序, 理論上反常能斯特效應的強弱在外爾半金屬中的決定性因素是材料在費米能級附近的電子結構是否能引起強的貝里曲率, 且這種內稟貢獻往往要遠大于外稟貢獻.

3.3 磁性狄拉克半金屬

本征的狄拉克半金屬中的狄拉克點同時兼具晶體空間翻轉對稱性與時間反演對稱性, 被稱為“三維石墨烯”.但是, 如果晶體空間翻轉對稱性或時間反演對稱性之一被破缺, 例如分別在非中心對稱的材料和磁性材料中, 此時的狄拉克點可能會演變為一對外爾節點, 狄拉克半金屬也因此會演變成外爾半金屬.晶體空間翻轉對稱性破缺的外爾半金屬已經在TaAs, WTe2等體系中發現, 而時間反演對稱性破缺的外爾半金屬直至近期才在磁性材料Fe3Sn2, FeSn等中發現.下面介紹在這些材料中的一些重要實驗進展, 主要包括巨反常霍爾效應、巨拓撲霍爾效應以及產生后者的可能的磁斯格明子等拓撲自旋結構, 這些效應在自旋電子、拓撲磁電等研究領域具有重要的價值.需要說明的是, 在磁性外爾半金屬中出現的巨反常霍爾效應、手性異常、拓撲增強的反常能斯特橫向熱電效應等均可能在磁性狄拉克半金屬中出現, 因此這些效應只能說明存在這類拓撲非平庸的電子結構可能會導致的量子效應, 這些效應并不是拓撲非平庸電子結構存在的直接證據.

3.3.1 巨反常霍爾效應

與磁性外爾半金屬類似, 在磁性狄拉克半金屬中由于在費米能級附近存在非零貝里曲率的狄拉克費米子能帶結構, 能誘導出巨大的反常霍爾電導.在意識到Fe3Sn2中存在狄拉克費米子的拓撲貢獻之前, 實際上已有實驗觀察到這一巨大的反常霍爾效應[114].在室溫下, 實驗測得Fe3Sn2的飽和霍爾電阻率為3.2 μΩ·cm, 幾乎比巡游鐵磁體Fe,Ni等高20倍; 反常霍爾系數為6.7 × 10—9cm/G,比Fe高3個數量級, 并且正比于縱向電阻率的3.15次方(即), 因此不能簡單地用skew或side-jump散射機制解釋, 當時將這種現象解釋為阻挫磁性[114].直至近期, 進一步的機理研究推測[30], 這一巨反常霍爾效應可能來源于本征的Karplus-Luttinger機制, 并指出材料的電子結構中可能存在由于雙層Fe kagome層的阻挫而形成的拓撲非平庸能帶結構, 這種拓撲電子結構可能是其巨反常霍爾效應的根源.最近的實驗進展[31]發現, 在Fe3Sn2中存在有質量的狄拉克費米子的跡象(圖9(a)), 由于內稟反常霍爾效應不依賴于散射機制, 內稟成分大小應該保持穩定且僅在縱向電導的平方接近零時存在.實驗上分離了內稟和外稟貢獻, 提取出來的內稟反常霍爾電導普遍存在于2—300 K的溫度區間, 值為(158 ± 16) Ω—1·cm—1,對應于每層kagome晶格貢獻約0.27e2/h的電導,而外稟的貢獻只在低于100 K的情況下才逐漸體現.對于Fe3Sn2中巨反常霍爾效應的研究普遍表明其物理根源是鐵磁狀態下雙層kagome晶格的基本對稱性和原子自旋軌道耦合的結果.

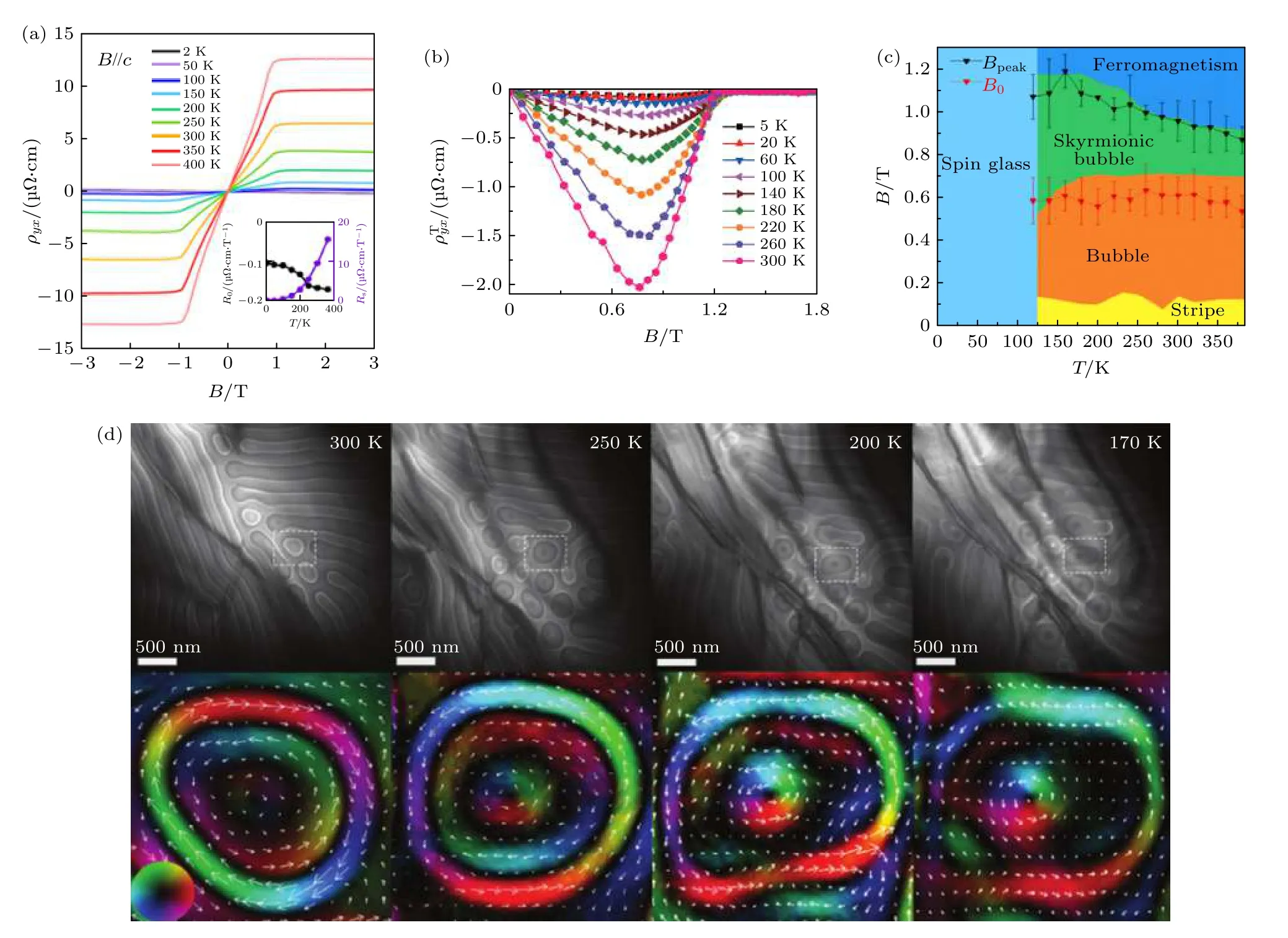
圖9 磁性狄拉克半金屬Fe3Sn2的反常霍爾效應、拓撲霍爾效應、磁斯格明子磁泡 (a)霍爾電阻率; (b)拓撲霍爾電阻率;(c)溫度-磁場下的相圖; (d)觀察到的斯格明子磁泡.圖(a)來自文獻[31], 圖(b)來自文獻[117], 圖(c)來自文獻[115], 圖(d)來自文獻[118]Fig.9.Anomalous Hall effect, topological Hall effect, and skyrmion bubble in magnetic Dirac semimetal Fe3Sn2: (a) Hall resistivity;(b) topological Hall resistivity; (c) a phase diagram of temperature and magnetic field; (d) the observed skyrmion bubble.(a) is adopted from Ref.[31], (b) from Ref.[117], (c) from Ref.[115], (d) from Ref.[118].

3.3.2 巨拓撲霍爾效應

在Fe3Sn2中, 由于缺陷、雜質、應力或化學配比起伏等原因, 可能形成非共面自旋構型, 使材料同時具有鐵磁性和阻挫自旋結構.磁性材料中的非共面自旋結構與材料的拓撲效應可能存在一定的聯系, 近年來引起了廣泛的關注.它主要來源于實空間晶格中標量自旋手性的貝里相位, 從而在實空間中產生一個等效磁場, 當載流子經過這一等效磁場時能感受到等效磁場對它運動時產生的作用力,這種作用力能對載流子輸運產生額外的偏離, 并能在霍爾效應的測量中體現出來, 即拓撲霍爾效應,亦稱為幾何霍爾效應.拓撲霍爾效應通常可在具有拓撲自旋結構(如磁性斯格明子、手性自旋結構等)的材料中觀察到, 尤其是在阻挫磁體中經常會觀察到此效應.近日對Fe3Sn2的研究中也觀察到了巨大的拓撲霍爾效應[115-117].如圖9(b)所示,Fe3Sn2在低場時呈現出巨大的拓撲霍爾效應, 在300 K和0.76 T環境下, 測量得的最大拓撲霍爾電阻率約為2.01 μΩ·cm; 當磁場大于1.3 T時,Fe原子的磁矩被完全磁化, Fe3Sn2的阻挫磁結構轉變成鐵磁性, 此時拓撲霍爾效應因此也消失[117].這種實空間的拓撲自旋結構一般只存在于特定的溫度、磁場范圍, 通過對溫度、磁場的調控能把材料體系的磁結構相圖刻畫出來, 如圖9(c)所示[115].與破缺材料對稱性的拓撲自旋結構不一樣, 這種拓撲自旋結構可以在一個中心對稱晶格中通過磁阻挫而穩定存在, 而這一效應可能是由于外磁場誘導的拓撲自旋結構和非線性自旋結構共同導致的.

3.3.3 磁斯格明子和磁泡

近年發現的以磁斯格明子為代表的實空間拓撲磁自旋結構的研究, 不僅為拓撲霍爾效應的來源提供實驗依據, 還有望為下一代自旋電子學器件的構建提供新方案.值得注意的是, 這里的物理載體不限于磁斯格明子, 還包括磁泡這一類研究多年的柱狀磁疇結構, 其關鍵點與磁斯格明子一樣, 具有實空間非平庸拓撲性, 即能使這些自旋結構具有高穩定性和抗干擾性.近期利用洛倫茲透射電子顯微鏡對Fe3Sn2進行研究[118,119], 觀察到了在特定溫度區間范圍內存在類斯格明子的復雜磁泡、磁渦旋結構, 如圖9(d)所示.但這些復雜磁結構不能用傳統磁泡理論來解釋, 通過模擬這些磁泡的三維磁結構及其厚度方向積分的面內磁化分布可知, 洛倫茲透射電鏡觀測的磁結構并非簡單的二維磁疇, 而是具有三維厚度調制的三維磁疇.這一結果為進一步研究磁性狄拉克半金屬中拓撲霍爾效應、磁斯格明子等自旋結構提供了直接的實驗支撐.

4 展 望

拓撲物理學領域已經歷約十年的發展歷程, 針對拓撲相和拓撲相變的研究仍十分火熱.從材料角度而言, 無論是非磁性還是磁性的絕緣體、半金屬、金屬, 它們的拓撲物理研究都取得了極大的成功.不僅其中的物理新穎, 這些材料還有其獨特的優勢, 例如它們的對稱性和電子結構對磁結構非常敏感, 往往磁結構、磁各向異性會對材料的拓撲特性起非常重要的影響.該拓撲電子態對外界的干擾、內部的缺陷、雜質等作用下仍具有拓撲穩定性,電子的自旋與動量相互鎖定.同時, 人們可以非常方便地利用外加磁場、電場來操縱它們的磁序乃至拓撲特性, 這些特點使得層狀磁性拓撲材料在自旋電子器件等功能器件中有重要的研究價值和應用前景.

作為層狀磁性材料和拓撲材料的交叉領域, 層狀磁性拓撲材料的家族成員至今仍比較少, 亟待進一步的開發和探索.一個很重要的例子是, 當前實現量子反常霍爾效應一般是在磁摻雜拓撲絕緣體或者MnBi2Te4家族材料中, 但是實現效應的最高溫度仍遠低于液氮溫度, 這是由此類材料仍存在樣品質量等各種相關的問題共同導致的, 因此探索更理想的體系材料是一個極為重要的科學問題.另外, 在尋找新材料的同時, 還需要專注于其中的一或兩種性能優越、有潛在提升價值的層狀磁性拓撲材料, 進行更為深入的研究, 并在這些材料基礎上進一步探究其中的物理, 對材料進行量子調控等深入研究, 也能對新材料的探索作支撐和輔助作用.