基于綜合指數法的無砟軌道配筋方案檢算與分析

高 亮 ，趙聞強 ，鐘陽龍 ，仝鳳壯

（北京交通大學土木建筑工程學院，北京 100044）

無砟軌道具有高平順、高穩定、高可靠性等優勢，在我國高速鐵路和城市軌道交通線路得到了廣泛的應用[1].無砟軌道是典型的鋼筋混凝土結構，從結構及功能上，基本可將配置的鋼筋分為軌道板普通鋼筋、軌道板預應力筋、底座板鋼筋及一些特殊的鋼筋.例如以中國高速鐵路無砟軌道系統（CRTS）為例，軌道板/道床板配有一定數量的普通鋼筋，而在一些預制軌道板結構還額外配備了預應力筋對軌道板施加了預應力效應以改善其服役性能；除部分路基、隧道內結構采用素混凝土和HGT水硬性支承層外，在CRTSⅡ型、CRTSⅢ型板式無砟軌道底座板內均配置了鋼筋骨架；CRTSⅢ型板式無砟軌道還設置了門型筋、自密實混凝土整體配筋及凹槽加強配筋等特殊鋼筋以保證其特殊的功能定位[2].

目前國內外針對無砟軌道結構的配筋設計主流方法主要可分為容許應力法與極限狀態法，并在設計后利用相關公式對強度及裂縫寬度進行檢算.日本無砟軌道主要采用了容許應力法進行配筋設計，在嚴寒地區引入部分限界狀態設計法的預應力結構；歐美地區則以極限狀態設計法作為主流；我國主要采用了容許應力法設計[3]，但也有學者采用極限狀態法對CRTSⅢ型板式無砟軌道進行了配筋設計[4-5].針對內部鋼筋配置形式的研究，國內外學者已有一定的研究，其中很大一部分集中在由連續配筋混凝土路面（CRCP）發展而來的雙塊式無砟軌道（CRCT）上：王森榮[6]基于對雙塊式無砟軌道與配筋混凝土路面結構的對比分析，提出了我國雙塊式無砟軌道的道床板配筋要求；Cho等[7]針對配筋率對雙塊式無砟軌道拉應力、裂縫寬度等性能的影響初步探討了改變鋼筋位置對無砟軌道力學特性的影響；趙坪銳等[8-9]針對雙塊式無砟軌道連續道床板開展混凝土開裂特性模型試驗；任娟娟等[10-11]則計算了配筋對連續道床板裂紋的影響.此外，部分學者還對內部鋼筋失效、破壞后軌道結構受力性能進行了評估：趙磊等[12]對CRTSⅠ型板式無砟軌道部分預應力破壞后導致的附加荷載影響進行了分析，研究了不同位置、數量預應力筋破壞對軌道板附加荷載的影響；徐家鐸[13]對CRTSⅠ型板式無砟軌道預應力筋錨穴附近混凝土損傷進行分析.

綜合來看，現有無砟軌道配筋設計檢算方法仍主要集中于基于平截面假定的容許應力法或極限狀態法，設計后通過相關公式對材料強度及裂縫寬度進行檢算.按照傳統設計理念檢算時結構內鋼筋配筋率、特殊鋼筋數量等指標合格即檢算完成，對其結構及部件配筋后內部受力變形協調性等情況關注不多；對于鋼筋布置方式的研究也大多集中于無砟軌道配筋率改變及預應力鋼筋出現破壞時對無砟軌道對結構變形、應力的影響，少見針對無砟軌道內部鋼筋具體排布方式對其服役特性的研究.

基于此，本文借鑒綜合指數法構造了無砟軌道配筋檢算指標，并以無砟軌道板內部配筋為例，通過有限元方法建立了無砟軌道配筋檢算分析模型，研究了無砟軌道板內部鋼筋具體排布方式對無砟軌道服役性能的影響.其主要目的在于彌補既有配筋方法在鋼筋布置優化方面的局限，將配筋方案向可視、可調、精細化設計的方向發展.期望通過該方法的研究，只需在結構內力計算的基礎上對結構配筋進行細微調整，達到改善、均衡局部應力應變狀態的目的，從而進一步增強結構長期服役性能.

1 基于綜合指數法的配筋檢算指標構造

配筋方案的優劣在一定程度上影響了軌道板適應運營環境的能力.目前對軌道結構配筋表現進行評價時，大多采用了應力在某一路徑的直觀分布并比較其拉應力峰值，通用性不強，無法完全說明配筋方案改變帶來的受力差異對整體服役性能的影響，對結構內部的受力變形均衡性也關注不夠.為系統考慮結構相應特征，借鑒水質評價領域常用的綜合指數法，結合無砟軌道結構特點，提出能夠反映配筋后結構內部應力均衡、變形協調的配筋檢算指標.

1.1 基于綜合指數法思想的配筋指標構造流程

綜合指數法具有綜合性強及可比性高等特點[14]，本文基于其基本思想構造配筋檢算指標，主要流程如圖1所示.

圖1 配筋檢算指標構造流程Fig.1 Construction process of reinforcement check index

構造合理的配筋指標后，考慮到無砟軌道作為典型的板結構，在進行整體狀態評價時，從空間分析的角度將軌道板沿厚度方向分為多層，獲取單個指標的分量數據分布圖層X1與X2，以此避開原有的峰值、路徑評價方法在表征整體均衡性上的局限.確定權重因子后對各分量疊加運算，最終通過統計指標進行量化評價.

上述流程將應力均衡、變形協調特性分別獨立，并通過數據的正則化/標準化避免了數據符號的影響，又通過空間分析（圖層）以保證數據的連續性，使得原本的配筋后結構整體方案評價問題最終轉換為構造合適的正則化特征分量的問題.

1.2 整體應力變形水平特征分量的選擇

考慮到外力在變形過程中所做的功將全部轉化為內能儲存在彈性體內部，因此結構受力后的應變能增量為表征結構應力特征提供了一個合理的思路.參考第四強度理論中主要將形狀改變能密度作為材料發生塑性屈服破壞的依據，即達到單向拉伸時發生塑性屈服破壞的形狀改變能密度時，結構發生塑性屈服破壞[15]，本文也只考慮形狀改變能密度作為結構應力特征的表征指標.

在應變能密度中，對應的形狀改變能密度為

式中：σ1、σ2、σ3分別為結構的 3 個主應力；E為彈性模量；v為泊松比.

根據材料力學的概念，式（1）也可寫為

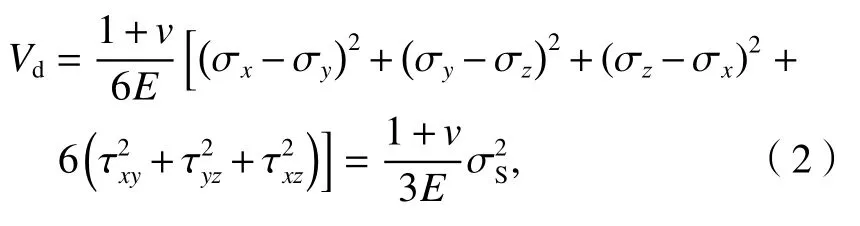
式中：σx、σy、σz分別為結構三向正應力；τxy、τyz、τxz分別為結構三向 切應力；σS為結 構von-Mises應力.

由式（2）可知，Vd綜合了結構各方向正、切應力及位移變化矢量，可作為結構整體應力特征分量X1.

1.3 受力變形均衡性特征分量的選取

在明確受力變形空間分布的基礎上，評價其均衡協調性宜采用相對量，而無砟軌道受力變形分布從幾何要素上可視為多個三維歐氏空間中的曲面.曲面上反映出的相對量特征可為本文尋求均衡性特征分量X2提供一定參考.

曲面曲率在一定程度上反映了曲面的質量，在各個曲率指標中，高斯曲率實際反映曲面的彎曲程度，當高斯曲率發生突變時，即發生曲率不連續時，結構已存在開裂等不連續問題.根據前期研究，軌道板受力變形分布不易出現反彎特征，也規避了高斯曲率為負的條件.本文選取高斯曲率作為結構均衡性分量的表征指標X2.當曲面表達為式（3）時，

高斯曲率K則為

圖2為某一層面產生變形后的位移分布及相對應的高斯曲率，由圖2可以很清晰地看出高斯曲率所代表的物理意義.

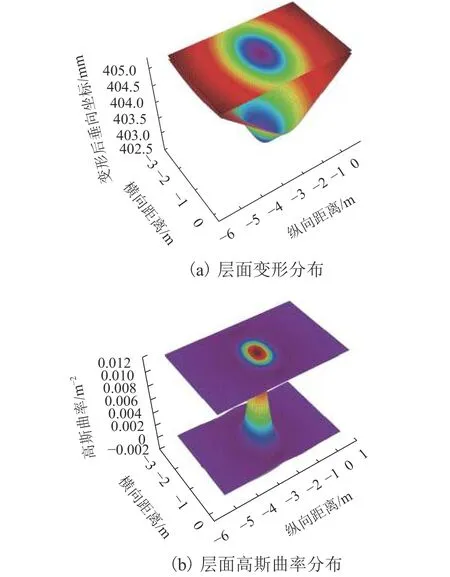
圖2 層面變形與高斯曲率分布Fig.2 Deformation and Gaussian curvature of structure layer

1.4 疊加計算及整體均衡性指標量化

在綜合指數法的具體實施過程中，將無砟軌道板結合單元劃分情況沿厚度方向劃分為多個圖層，于各層節點提取各點處形狀改變能密度及變形后高斯曲率.從物理意義上，形狀改變能密度中已包含了應力分量與位移矢量，此處曲面曲率的作用則是引入均衡性評判指標，即相當于通過定量評價位移變量的撓曲程度，將變形均衡系數引入應力特征分量中，因此確定其權重比為1∶1，并根據其正相關關系進行點乘得到最終整體圖層結構面某一點的結構受力變形綜合指數為

為了量化各方案間受力變形差異，借鑒軌道不平順評價指標中幅值管理及軌道質量指數（track quality index，TQI）的理念，選取結構各圖層結構受力變形綜合指數峰值及均方差進行對比，為消除由量綱和數據尺度帶來的影響，進一步提取變異系數進行對比.變異系數定義為標準差σ與平均值μ之比，即

2 無砟軌道配筋檢算分析模型

本文以CRTSⅢ型普通板式無砟軌道為例，應用文章提出的配筋評價指標，分析無砟軌道板內部鋼筋排布方式對其受力特性的影響.

2.1 無砟軌道數值仿真模型的建立

CRTSⅢ型普通板式無砟軌道自上而下分別由軌道板、自密實混凝土、底座板組成，但考慮經濟性取消了軌道板內雙向預應力筋.

鋼軌為CHN60軌，采用梁單元模擬；扣件采用多根三向彈簧-阻尼單元模擬，扣件間距為0.63 m，垂向靜剛度為45 kN/mm，橫向靜剛度為50 kN/mm，最大縱向阻力9 kN/組.

采用實體單元對軌道結構主體建模，軌道板采用C60混凝土，標準軌道板長5.6 m，寬度為2.5 m，厚度 0.2 m.自密實混凝土層厚度為0.09 m，寬度與軌道板相同；底座采用C40混凝土，寬度為2.8 m，厚度為0.3 m，底座上設置2 個尺寸為600 mm × 600 mm ×100 mm的凹槽，每塊底座板上設置3塊軌道板，軌道板間保有一定長度的伸縮縫[16].

本文采用桁架單元模擬軌道板縱、橫向主筋，認為其預制施工后鋼筋與混凝土間粘結良好，為計算便利，模擬鋼筋與軌道板單元相互作用時將鋼筋單元嵌入至軌道板單元內.模擬軌道板與自密實混凝土層間關系時，考慮門型筋對層間粘結作用的補強，將兩者共節點建模；對自密實混凝土與底座間的隔離層，將其模擬為法向可分離，切向存在一定摩擦的“硬接觸”行為；底座凹槽四周配備有緩沖墊層，模擬時將其定義為一定的接觸剛度；下部基礎采用路基彈簧進行簡化模擬，建模具體材料參數如表1所示[17].

表1 數值仿真模型材料參數Tab.1 Material parameters of numerical model

為消除邊界效應，模型計算長度取三塊底座板長度，并以中間底座板的正中軌道板作為分析對象，所建立的無砟軌道配筋檢算模型如圖3所示.

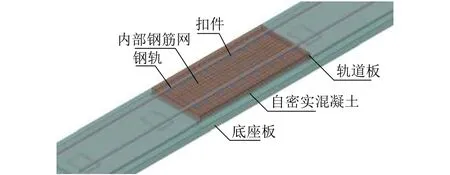
圖3 CRTSⅢ型普通板式無砟軌道配筋檢算模型Fig.3 Reinforcement checking calculation model of CRTS Ⅲ ordinary steel type slab track

2.2 配筋工況設計

依據相應荷載下結構內力，采用傳統的配筋設計方式對該無砟軌道板進行鋼筋配置方案的初步設計.設計結果表明，為滿足配筋率要求，橫向鋼筋面積應不小于 4720.1 mm2，縱向配置鋼筋面積應不小于3618.3 mm2.為了保證鋼筋骨架的成型，將橫、縱向鋼筋按兩排進行布置，在保證構造要求及保護層厚度的前提下，選用多種直徑及數量的鋼筋進行配筋方案的具體設計.

在設計不同軌道板鋼筋排布方式時，以相同配筋率為基本設計原則，考慮實際施工、絕緣等要求，選取了?12～?16的HPB300鋼筋進行排布.首先配置了整體較為稀疏、鋼筋直徑較大的方案1；減小鋼筋直徑，增加了鋼筋數量將鋼筋盡量滿布至軌道板內，并在軌下位置適當加密，以此設置了方案2；之后考慮車輛荷載下彎矩分布在軌道板內對應承荷位置鋼筋間距進一步加密，基于此對方案2 進行調整設置了方案3（為保證骨料咬合最密間距為兩倍保護層厚度），具體方案情況如表2所示，各方案橫縱向鋼筋在軌道板內部的具體位置采用紅色線條表征，見表3.

表2 保證相同配筋率條件下不同普通鋼筋配置方案Tab.2 Different reinforcement arrangement scheme under same reinforcement ratio

表3 橫縱向鋼筋在軌道板內部的具體位置Tab.3 Specific position of transverse and longitudinal reinforcement inside the rail plate

在檢算過程中，考慮到不同方案在不同荷載下表現有所區別，本文以無砟軌道服役時所受長期荷載內較為典型的車輛荷載與溫度荷載為例，對其荷載效應影響下的軌道板服役狀態進行分析.其中車輛垂向荷載以CRH3型車為例，根據《高速鐵路設計規范》[18]取為三倍靜輪重225 kN，溫度荷載取整體升溫 45 ℃、整體降溫 40 ℃、正溫度梯度 90 ℃/m及負溫度梯度45 ℃/m，溫度梯度單獨加載軌道板.

3 不同鋼筋配置方案檢算分析

3.1 車輛荷載下不同方案表現分析

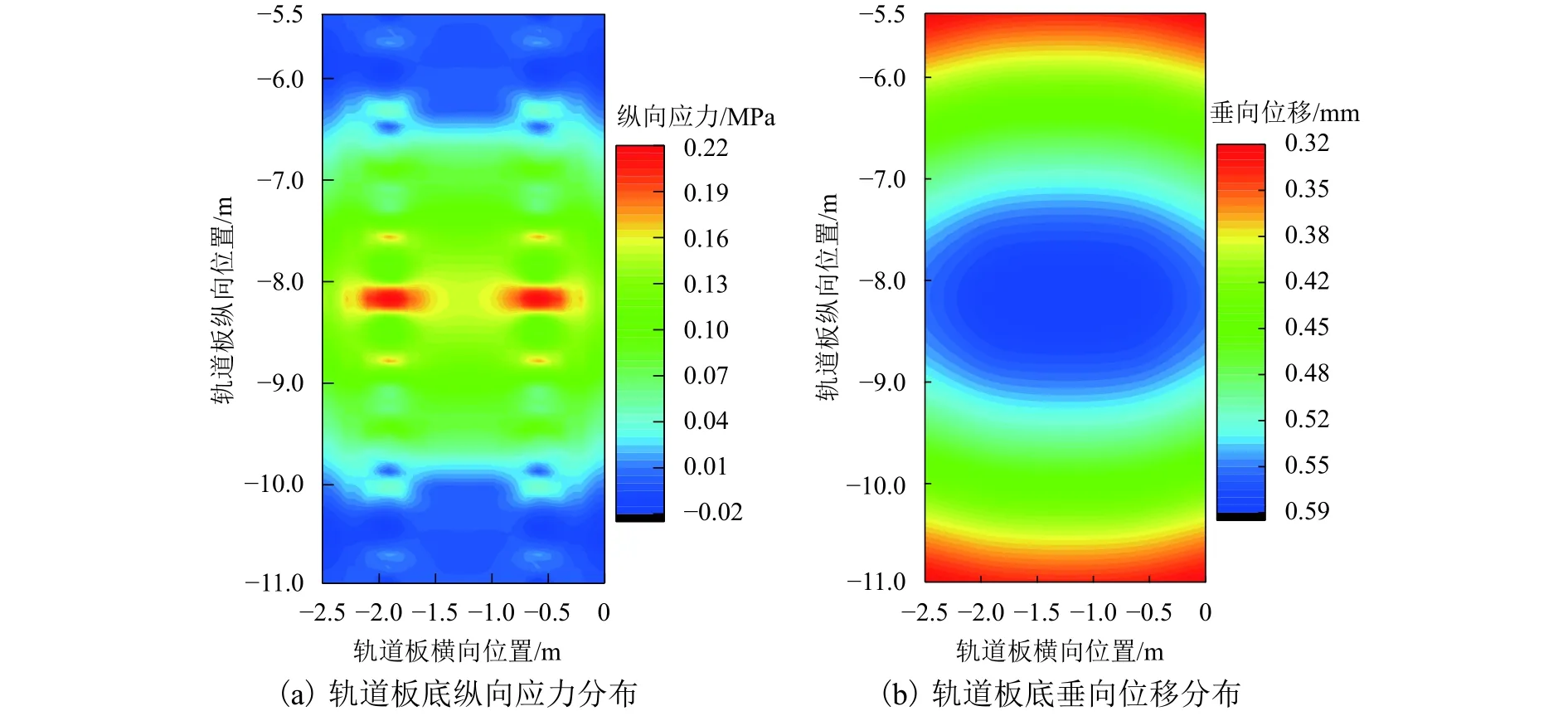
首先對綜合指數作評價指標的效果進行驗證.以車輛荷載作用下方案1為例，施加垂向車輛荷載后，提取軌道板板底縱向應力、垂向變形以及板底、板頂受力變形綜合指數分布如圖4（a）～（d）所示.

由圖4可知，在分布形式上，相較于傳統的縱向應力、垂向位移指標，綜合指數峰值主要集中分布于直接承受車輛荷載的扣件位置，更能集中反映出軌道板整體的不均衡點（此處為扣件支承效應）.

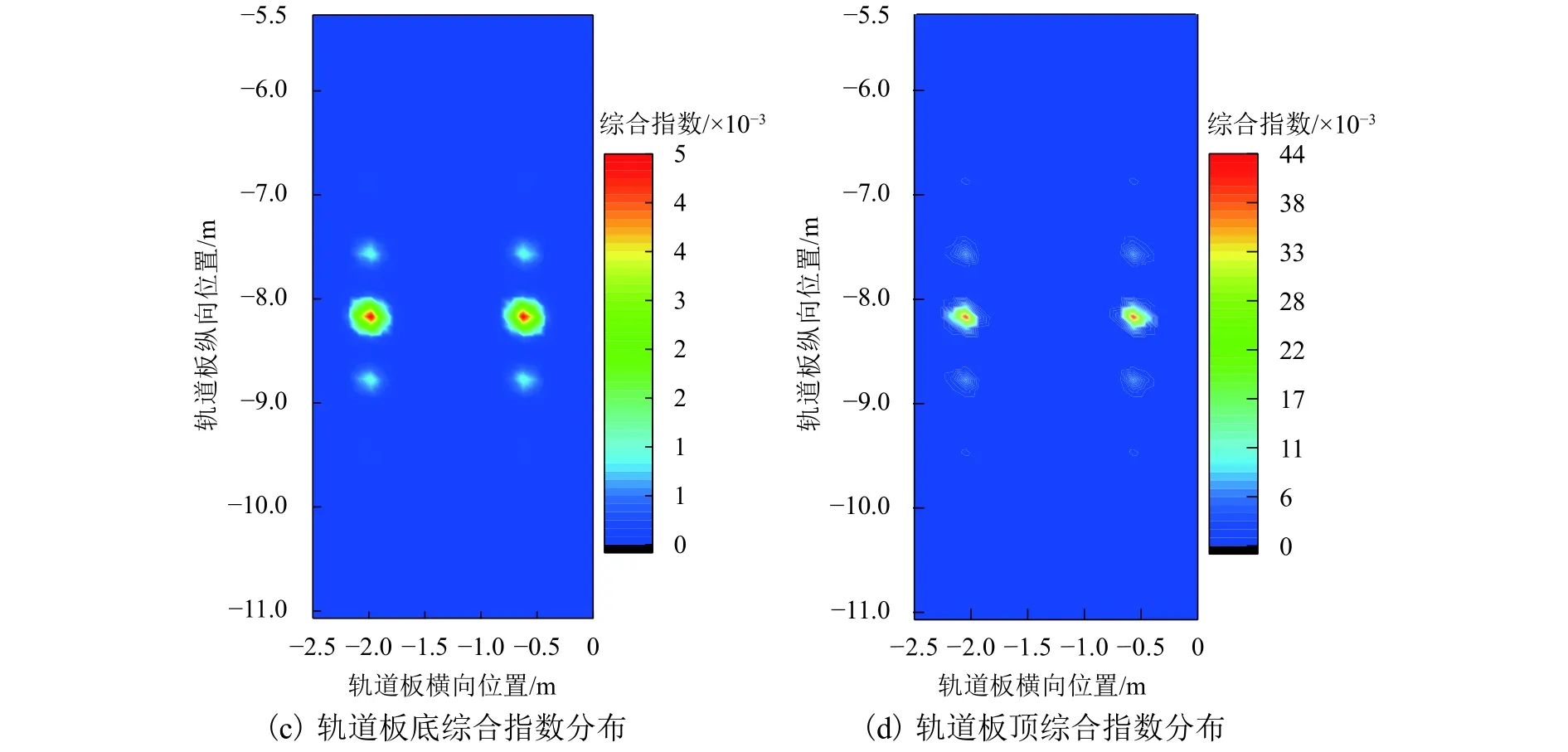
圖4 車輛荷載作用下軌道板典型力學指標分布（方案1）Fig.4 Distribution of typical mechanical indexes of track slab under vehicle load (scheme 1)

為定量比較綜合指數指標對差異率的貢獻，提取不同力學指標的統計值如表4所示.

表4 車輛荷載作用下不同普通鋼筋配置方案下板底指標對比Tab.4 Comparison of statistical indexes of bottom of track slab for each scheme under vehicle load

由表4可知：3個方案在各指標上均有不同程度的差異；以量值差異較大的方案1與方案3為例，方案3在縱向應力、垂向位移的峰值較方案1分別下降了8.3%和6.1%，而在綜合指數峰值上差異率達到了16.3%；在均方差與變異系數指標上，兩方案的綜合指數也較傳統指標差異更大.

即使在荷載經過傳遞更為分散的軌道板底，綜合指數較傳統指標也體現出更大的差異率，說明本文提出的綜合指數在局部配筋細微調整評價方面效果更好，對鋼筋排布方案的檢算更具適應性.

本文在空間分析時將軌道板依據網格情況沿厚度方向分為多個圖層，以板寬與板長方向作為圖層的基本坐標系.由圖4（c）和圖4（d）可知：不同于有砟道床的散體結構，軌道板的相同坐標節點在厚度方向各指標變化呈現出連續性，即只需通過提取頂面與底面圖層來綜合評價結構配筋后整體表現.

為更全面地評價3種方案在受力均衡性上的優劣，進一步提取分布較為集中的板頂綜合指數統計指標量值如表5所示.

相對其他層面，頂面綜合指數指標量值最大，且差異更為顯著，由表5可知：方案1相對方案2在各指標上均有不同程度地增加；方案1綜合指數峰值與均方差較方案2增加了20.5%，說明此時方案1的均衡性表現更差；方案3較方案2在綜合指數峰值、均方差、變異系數指標上均有減小，說明此配筋方案在鋼軌軌下位置確實對軌道承載剛度有一定程度的加強.

表5 車輛荷載作用下不同普通鋼筋配置方案下板頂各綜合指數指標對比Tab.5 Comparison of statistical indexes of track slab top for each scheme under vehicle load

綜合車輛荷載作用下各配筋方案表現，可認為方案3表現最佳，方案2次之，方案1表現最差.

3.2 整體升溫荷載下不同方案表現分析

以整體升溫作用下方案1為例，對軌道結構施加整體升溫45 ℃后，提取軌道板板頂及板底的受力變形綜合指數分布如圖5（a）、（b）所示.

由圖5（c）、（d）可知，在整體升溫荷載作用下軌道板熱脹變形受到了來自上部扣件的約束作用，軌道板板頂能夠看出明顯的扣件支承約束效應.軌道板綜合指數峰值均出現在軌下板端位置處.提取各方案軌道板頂、板底受力變形綜合指數的各統計量進行橫向對比如表6所示.

圖5 整體升溫下軌道板板頂、底綜合指數分布Fig.5 Comprehensive index distribution of top and bottom of track slab under overall temperature rising load

表6 整體升溫作用下不同普通鋼筋配置方案板頂、底各綜合指數指標對比Tab.6 Comparison of comprehensive statistical indexes of different schemes under overall temperature rising load

由表6可知：綜合對比3種配筋方案軌道板受力變形情況，從方案1到方案3，各綜合指數統計指標均有不同程度的變化；其中方案2在軌道板頂面與底面綜合指數峰值上分別較方案1減小了13.58%和34.67%；但方案3軌道板頂面在綜合指數峰值方面較方案1增大了一倍有余.對比各方案綜合指數的均方差與變異系數也能發現類似的規律.

對比圖5后發現：方案1與方案3軌道板受力變形綜合指數分布相似，兩方案在板中等大部分位置量值也基本接近，只在峰值處（即軌下板端位置）有非常明顯的區別，說明此時方案3在軌道板端部受力更不均衡.這也解釋了方案3與方案1的變異系數與標準差存在較大差異的現象.

提取各方案鋼筋von-Mises應力分布云圖進行對比，如圖6.

由圖6可知：3種方案鋼筋von-Mises應力峰值差異不大，且均遠遠小于300 MPa的限值，說明此時3種方案的鋼筋都處于正常工作范疇；相較于方案1與方案2，方案3在集中布置的縱向主筋端部的von-Mises應力分布更大，集中布置鋼筋后，此處鋼筋溫度力增加明顯，并集中傳遞至軌道板混凝土端部.很好地解釋了方案3軌道板的綜合指數在端部較方案1與方案2有顯著增加的現象.

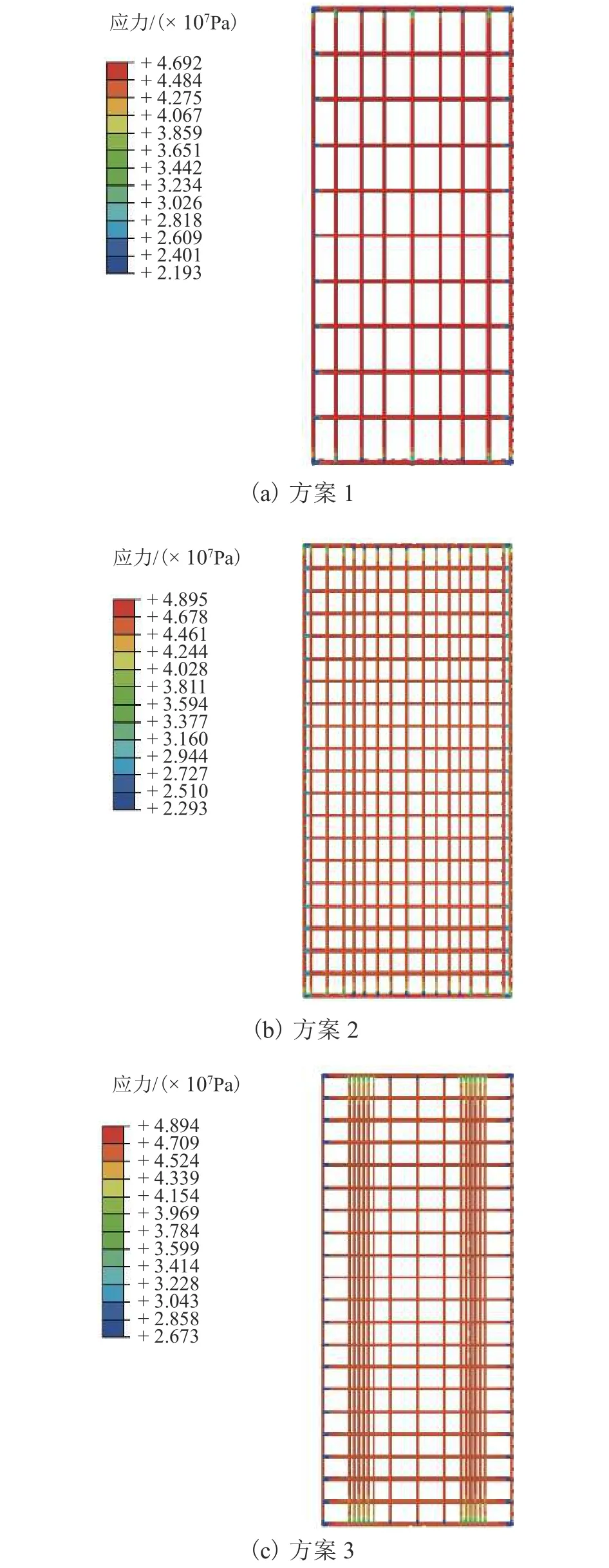
圖6 整體升溫時各方案鋼筋 von-Mises應力分布Fig.6 von-Mises stress distribution of reinforcement of different schemes under overall temperature rising load

綜合對比3種配筋方案在整體升溫荷載下的表現可知：方案2要優于配筋數量較少、鋼筋直徑更大的方案1；由方案3結果可以發現，在對應軌下位置集中配置縱筋后，該處由鋼筋溫度力集中于端部區域，使得軌道板端部受力增加；盡管鋼筋與混凝土的溫度線膨脹系數相近，當溫度變化時，二者之間不會產生較大的相對變形，但此時端部集中的配筋仍然導致軌道板受力更不均衡.

對整體降溫荷載下3種配筋方案進行分析也可得出類似的規律，限于篇幅，在此不再贅述.

3.3 正負溫度梯度下不同方案表現分析

對軌道板施加正溫度梯度90 ℃/m與負溫度梯度45 ℃/m后，提取各方案軌道板頂、板底受力變形綜合指數的各統計量如表7所示.

由表7可知：正溫度梯度作用下，3種方案在頂面綜合指數上的差異較小，各統計指標主要差別集中在底面；對比底面各指標可知，方案2較方案1在綜合指數峰值上減小了11.97%，綜合指數均方差減小了8.4%，變異系數減小了14.4%；此時方案2軌道板受力更為均勻，說明此時方案2軌道板受力更為均勻；方案2與方案3基本一致，與方案1存在差異；負溫度梯度作用下各方案綜合指數統計指標無明顯差異.

表7 正、負溫度梯度作用下不同普通鋼筋配置方案綜合指數指標Tab.7 Comprehensive index of different reinforcement schemes under positive and negative temperature gradients

綜合本文3種方案在不同荷載下的檢算結果，由上述一系列定性、定量分析，以方案2為基準，將不同方案進行比較如表8所示.

表8 不同荷載作用下各方案綜合比較（以方案2為參照）Tab.8 Comparison of different schemes under different loads (referring to scheme 2)

由表8可知：除了車輛荷載作用下方案3較方案1、2服役性能略有提升，綜合其余工況，方案2要明顯好于方案1、方案3；方案1配筋數量較少，配筋方式過于分散，在承受不同荷載時其表現較其余兩方案更差；方案3中過于集中的配筋在加強結構局部剛度的同時反而破壞了原有的協調性，可能會在承受復雜溫度荷載時帶來新的問題，此外，在局部過于集中的配筋還有可能導致局部的超筋破壞風險，并對施工造成影響.因此，鋼筋排列密布且軌下適度加密排布的方案2對復雜服役環境環境適應性更強，其布置方案較為合理.

4 結 論

本文基于綜合指數法構造了無砟軌道結構配筋檢算指標，并通過有限元方法建立了無砟軌道配筋檢算分析模型，研究了鋼筋排布方式對無砟軌道力學性能的影響，主要結論如下：

1）在配筋檢算時，可將結構的形狀改變能密度與曲面高斯曲率基于綜合指數法思想結合，以評價結構配筋后應力、變形均衡性.

2）相較傳統應力指標變形，本文提出的綜合指數在分布上能更好地突出不均勻區域；在量化方案評價時指標間具有更大的差異率，在評價調整配筋方案時更具適用性.

3）在滿足配筋率的前提下于軌下位置額外密布鋼筋，能夠在一定程度上增強剛度，提升軌道板抵抗垂向車輛荷載的能力.

4）軌下位置過于集中的配筋在加強結構局部剛度的同時反而破壞了整體的均勻性，尤其在整體升降溫荷載下軌道板端部綜合指數明顯升高，較均勻密布工況增大了近1倍.

綜合來看，滿足配筋率與構造要求的情況下，選擇鋼筋直徑較小、排列更為密布的鋼筋方案并在軌下位置適度加密，更能夠改善軌道板在不同環境下的受力狀態，使其在控制裂紋、結構耐久性上能夠保持更為優越的長期服役性能.本文關注了軌道結構受力的均衡性特征并對在評估方法方面進行了一定的嘗試，未來還可結合進一步的理論研究，提出更為完善的均衡性評估指標.