側邊加勁半圓形波紋鋼板墻的抗側性能

周林麗 ，譚 平 ，滕曉飛

（1.廣州大學廣東省地震工程與應用技術重點實驗室，廣東 廣州 510405；2.廣州大學工程抗震減震與結構安全教育部重點實驗室，廣東 廣州 510405）

剪力墻按材料分為鋼筋混凝土剪力墻、型鋼混凝土剪力墻、配筋砌塊剪力墻和鋼板剪力墻，其中以取材方便、工藝簡單、整體性好且抗側移能力較好的鋼筋混凝土剪力墻的研究應用最為廣泛成熟[1-2].混凝土剪力墻及砌塊剪力墻通常因自重較大提高了框架梁柱的截面尺寸要求，且混凝土剪力墻及砌塊剪力墻因耗能能力較差震后損壞嚴重給震后修復帶來不便.鋼板剪力墻作為一種新型抗側力構件除具有較好的抗側移能力外，相較于鋼筋混凝土剪力墻其自重輕、震后易更換、且耗能能力強，這些特點使得鋼板剪力墻在20世紀70年代便廣泛應用于北美和日本高地震烈度區的多高層鋼結構建筑中[3-4]，其形式主要為平鋼板剪力墻.平鋼板因其平面外剛度小、受剪易屈曲及屈曲后結構的抗側剛度急劇下降等因素給運輸安裝及結構的側移控制帶來諸多難題.

相對平鋼板而言，波紋板的波形使鋼板的面外剛度較大，其屈曲荷載也是同厚度平鋼板的幾倍至幾十倍[5-6]，將其作為抗側力構件將會大大改善平鋼板剪力墻極易發生彈性屈曲的不足，充分發揮鋼板的延性及承載力.

目前波紋鋼板在波紋腹板工形構件中的應用在國內外均已比較成熟，我國已將其納入技術規程[7-8].而將波紋鋼板應用于鋼板剪力墻結構的研究起步較晚：Berman和Bruneau[4]首次對一斜向放置的梯形橫截面波紋鋼板墻進行了低周反復加載試驗，試驗結果表明，斜向波紋鋼板墻的抗側剛度及延性都得到了提高，其滯回環面積較大，但仍出現了較大的捏攏且滯回曲線并不對稱的問題；Botros[9]采用有限元軟件ADINA對橫向梯形波紋鋼板剪力墻及平鋼板剪力墻進行了滯回分析，表明波紋鋼板剪力墻比平鋼板剪力墻具有更大的抗側剛度、較高的承載力及更飽滿的滯回環；蘭銀娟等[10-18]也先后對截面形式為梯形、波浪形、三角形、正弦波形及鋸齒形的波紋鋼板剪力墻進行了理論分析及試驗研究，結果顯示波紋鋼板剪力墻在延性、初始剛度及耗能性能方面均比平鋼板剪力墻有顯著提高.但目前對于截面為半圓形的波紋板國內外并沒有相關研究，半圓形波紋板因制作簡單方便，可將其應用于鋼板剪力墻結構.

本文由此提出一種新型側邊加勁半圓形波紋鋼板剪力墻，為研究側邊加勁半圓形波紋鋼板剪力墻能否實現“屈服先于屈曲”，首先建立了側邊加勁半圓形波紋鋼板剪力墻的簡化力學模型，根據力學模型推導了側邊加勁半圓形波紋鋼板墻的彈性初始剛度及承載力公式；然后采用有限元分析軟件ABAQUS對其進行彈性屈曲分析及非線性推覆分析，給出了側邊加勁半圓形波紋鋼板剪力墻的彈性屈曲臨界應力公式；并分析不同參數變化對波紋鋼板剪力墻抗側性能的影響及規律，為側邊加勁半圓形波紋鋼板墻設計參數的選取提供意見和建議.

1 側邊加勁半圓形波紋鋼板墻的構造

波紋鋼板墻的截面形式有多種，本文突出分析半圓形的波紋鋼板，其特點為：截面由若干個半圓組成；為便于門窗洞口的布置，與邊緣框架的連接方式采用兩邊連接（即鋼板僅與框架梁連接）；波紋采用豎向設置，使波紋鋼板可以抵抗豎向荷載的作用；波紋鋼板左右兩側設置加勁肋以防止鋼板側邊的局部屈曲，同時也為波紋鋼板屈曲后形成的拉力帶提供了一定的錨固作用，其結構形式和幾何參數如圖1所示.圖1 中：b為波紋板板寬；h為板高；tw為板厚；d為圓形直徑；r為波幅（圓形半徑）；q為波長；bf為肋寬；tf為肋厚.為表述方便，后文中將側邊加勁半圓形波紋鋼板剪力墻統一簡稱為CSPSW.

由圖1（a）可知：對于側邊加勁半圓形波紋鋼板剪力墻，相較平鋼板剪力墻，其截面設計參數僅增加一項r；相較其他截面形式的波紋鋼板墻，其設計參數大大減少.側邊加勁半圓形波紋鋼板墻的總體構造如圖1（b）所示，波紋鋼板墻通過魚尾板采用高強螺栓（或焊接）與上下框架梁連接，側邊加勁不與框架梁連接.

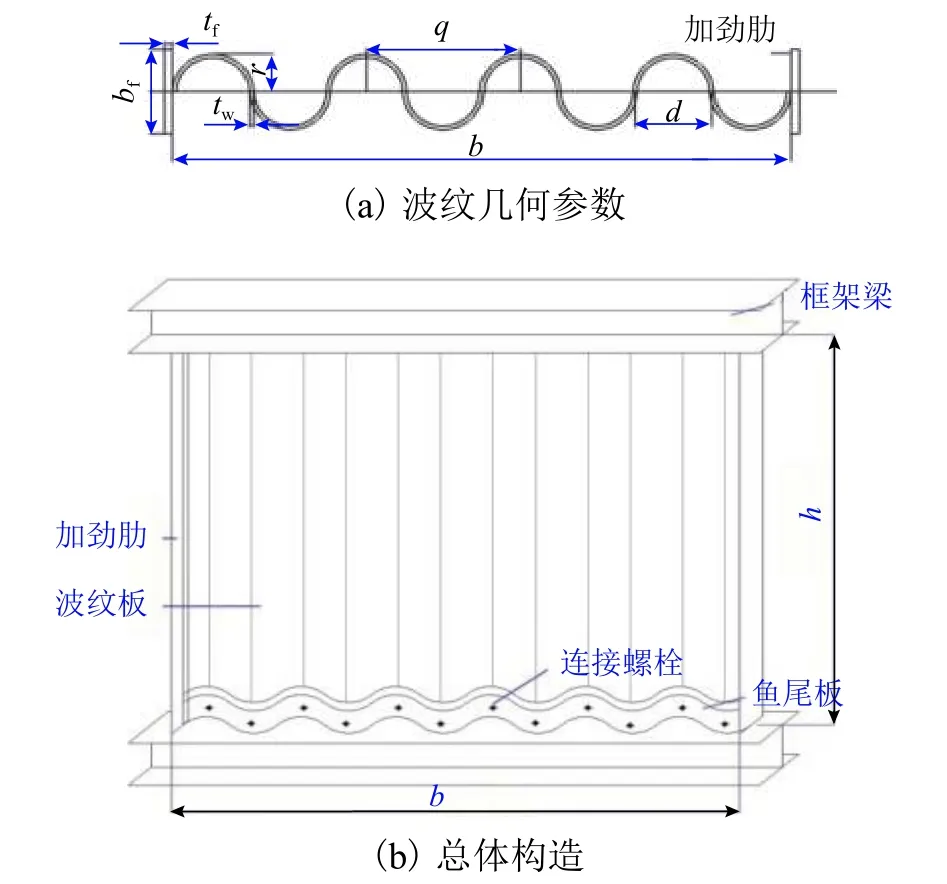
圖1 側邊加勁波紋鋼板墻Fig.1 Schematic diagram of CSPSW

2 力學模型建立

2.1 簡化力學模型

為研究側邊加勁半圓形波紋鋼板墻的抗側性能，假設與鋼板墻相連的上下框架梁的剛度為無窮大，在水平荷載V作用下，側邊加勁半圓形波紋鋼板墻可視為兩端固定構件，其簡化力學模型如圖2（a）所示，在水平荷載V作用下的彎矩、剪力分布如圖2（b）、圖2（c）所示.

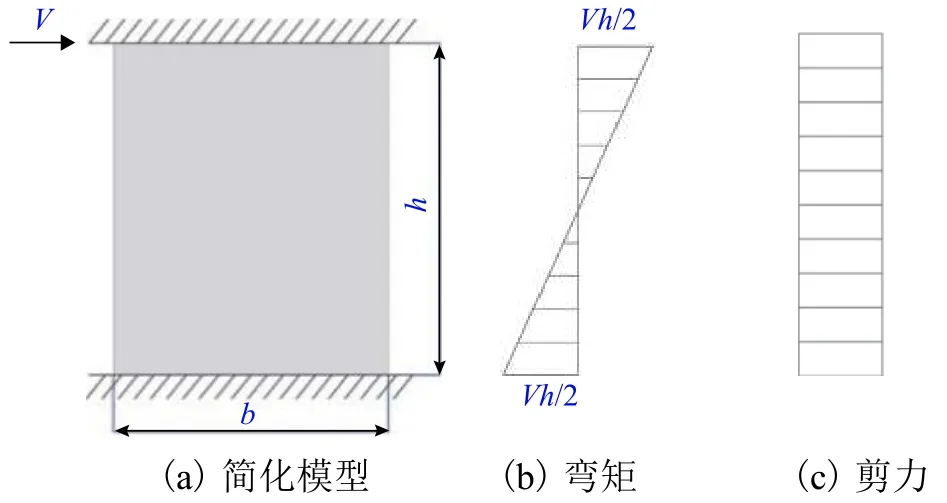
圖2 波紋鋼板墻簡化力學模型Fig.2 Simplified mechanical model of CSPSW

根據文獻[19]可知：鋼板在水平荷載V作用下的總水平位移Δx由彎矩引起的位移ΔxM和剪力引起的位移ΔxV組成，即

經計算可得

式中：Es為鋼材彈性模量，N/mm2；I為鋼板截面慣性矩，mm4；Gs為鋼材剪切模量，N/mm2；A為鋼板截面面積，mm2；k為考慮剪應力在截面上分布不均的修正系數，對于薄壁環形截面，k=2.

2.2 彈性初始剛度理論公式

假設圖2（a）中板寬為b的波紋鋼板由2n個半圓形組成，則有2n×2r=b，A=πtwb，根據文獻[20]波紋鋼板墻的截面慣性矩為

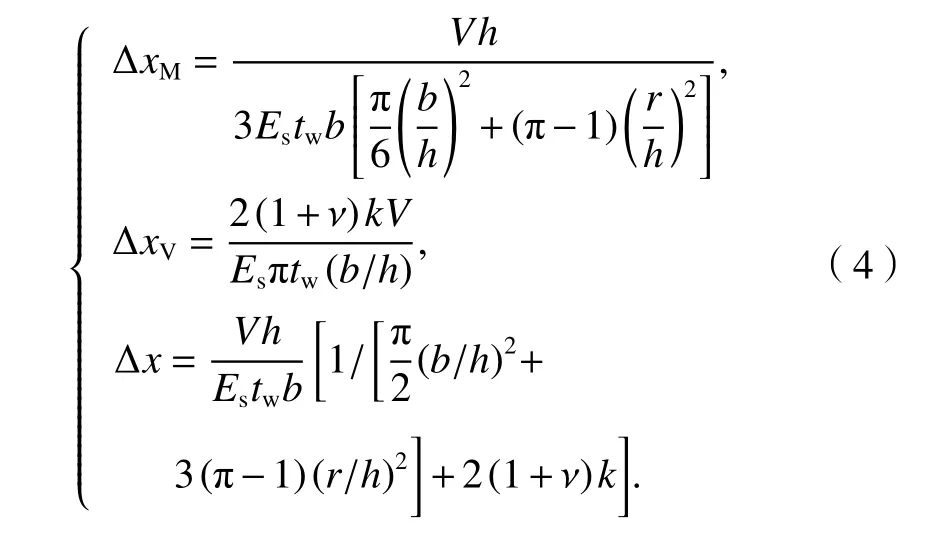
由V與Δx在彈性階段的關系：V=K0Δx可得，側邊加勁半圓形波紋鋼板剪力墻的彈性初始剛度K0為

從式（4）可見，波紋鋼板墻的剪切變形與圓形半徑無關，在水平荷載作用下鋼板墻的剪切變形與總變形之比為

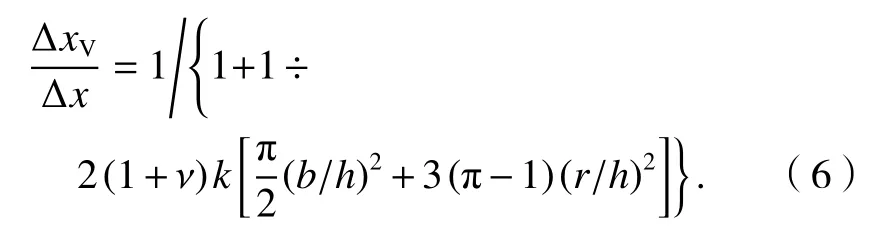
2.3 承載力理論公式

對于兩邊連接側邊加勁半圓形波紋鋼板墻，其在水平荷載作用下上、下兩邊產生的彎矩M最大，如圖2（b）所示，滿足

而構件在彈性階段的最大彎矩為

式中：We為鋼板彈性抗彎截面模量；fy為鋼材的屈服強度.

于是得到

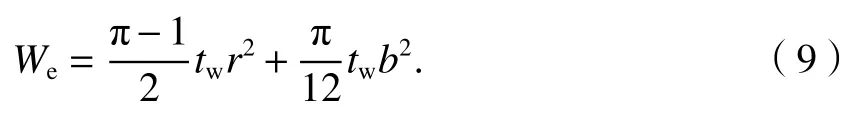
由式（7）、（8）、（9），可得側邊加勁半圓形波紋鋼板墻的屈服荷載為

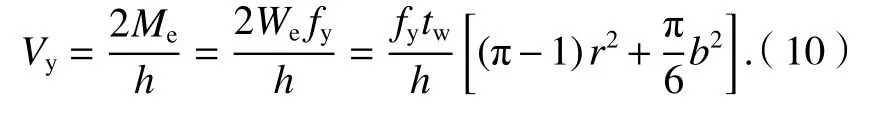
極限荷載為

式中：Mu為截面塑性彎矩；Wp為塑性抗彎截面模量，如式（12）.

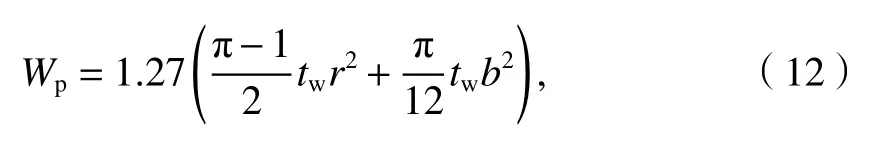
將Wp代入式（11）得到

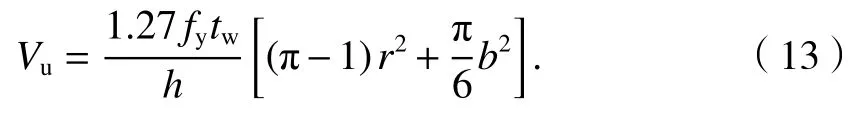
2.4 彈性屈曲臨界荷載

郭彥林等[18]以正弦波浪鋼板為例，利用有限元軟件對四邊簡支純剪切作用下的波浪鋼板墻進行彈性屈曲分析發現，在常用尺寸范圍內，波浪鋼板墻的屈曲模態為整體屈曲，根據有限元計算結果擬合得到整體屈曲下，四邊簡支波浪鋼板墻彈性剪切屈曲臨界應力為

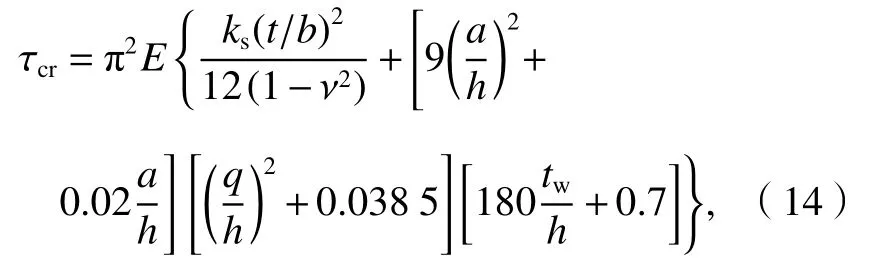
式中：E為鋼板的彈性模量；a為波浪形波紋鋼板的波幅；ks為與邊界條件有關的鋼板受剪屈曲系數.

3 理論公式驗證

3.1 有限元模型

利用ABAQUS對側邊加勁半圓形波紋鋼板墻進行數值模擬，將波紋鋼板與邊緣框架組裝并建立的單層波紋鋼板有限元模型如圖3所示，為研究側邊加勁半圓形波紋鋼板剪力墻的主要設計參數（跨高比β=b/h、高厚比λ=h/tw、d、bf、tf）對半圓形波紋鋼板剪力墻受力性能的影響，本文以不同b、tw、d、bf、tf參數建立了 19個不同幾何參數的側邊加勁半圓形波紋鋼板剪力墻模型，其中B-0為基本模型，其 模 型 參 數 為b=3000mm、h=3000mm、tw=3mm、d=60mm、bf=100mm、tf=10mm；在 其余參數不變的情況下，模型B-1、B-2僅改變模型B-0 的板寬，b分別取 1500 mm、6000 mm；模型B-3～B-6 僅改變模型 B-0 的板厚，tw分別取 4、5、6、9 mm；模型B-7～B-10僅改變模型B-0的直徑，d分別取 30、80、90、120 mm；模型 B-11～B-14 僅改變模型 B-0 的肋寬，bf分別取 60、150、200、250 mm；模型B-15～B-18僅改變模型B-0的肋厚，tf分別取6、9、15、18 mm；模型 B-19～B-21 為作對比的平鋼板剪力墻模型，d為0，b分別取 1500、3000、6000 mm.

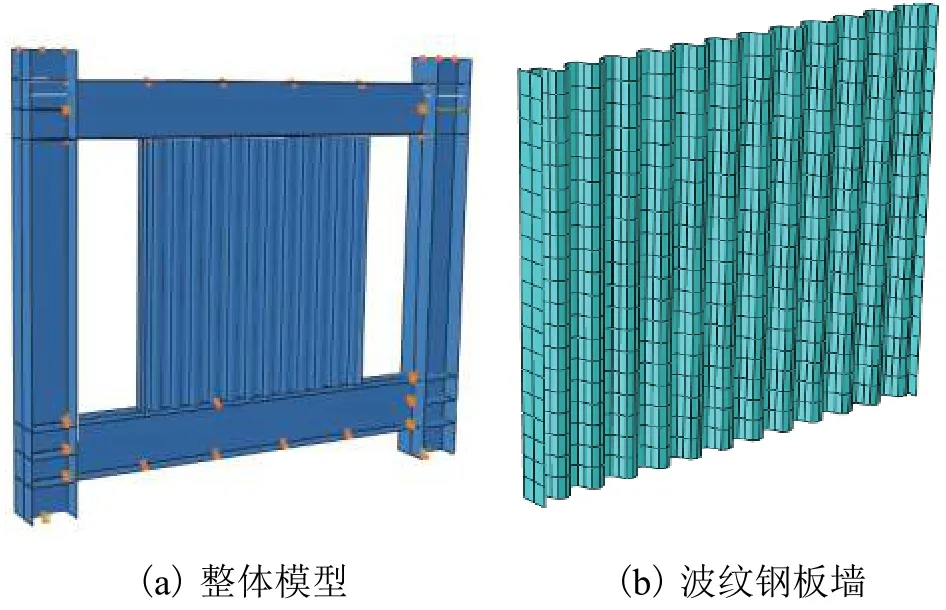
圖3 有限元模型Fig.3 Finite element model

3.2 材料模型和單元選取

模型中假設邊緣梁、柱構件剛度無窮大，且兩者鉸接連接，以保證邊緣構件不提供任何抗側剛度，由波紋鋼板承擔全部剪力.為保證結構中波紋鋼板墻先于主體結構屈服耗能，加勁肋及邊緣梁、柱采用Q345級鋼材，波紋鋼板采用Q235級鋼材，鋼材的應力-應變關系采用理想彈塑性模型，對于梁柱材料Q345，屈服強度取 345 MPa；鋼板材料 Q235，屈服強度取 235 MPa，彈性模量E=2.06 × 1011Pa，泊松比ν=0.3.模型采用殼單元S4R模擬加勁肋、邊緣梁、柱及波紋鋼板.

3.3 邊界條件

根據實際工況，有限元模型采用如下邊界條件：約束柱底節點所有平動及轉動自由度，以模擬底部固接；為模擬上部樓板對梁的支撐作用，約束梁腹板及節點域所有節點的平面外自由度；采用Hinge連接單元模擬梁柱之間鉸接；為保證梁與波紋鋼板之間的荷載傳遞，波紋鋼板上、下兩端分別與附近的梁節點采用綁定約束.

3.4 理論公式驗證

對圖3中的有限元模型進行單調加載分析，為考慮結構的幾何非線性，將彈性屈曲分析所得到的一階屈曲模態的1%作為初始缺陷施加在有限元模型上.取位移-荷載關系曲線中的極值點作為極限荷載，采用通用屈服彎矩法確定屈服荷載，將由式（5）、（11）及式（13）計算得到的彈性初始剛度、屈服荷載及極限荷載理論解與數值解進行對比，對于平鋼板墻不再適用，故平鋼板墻僅給出數值解，結果見表1.

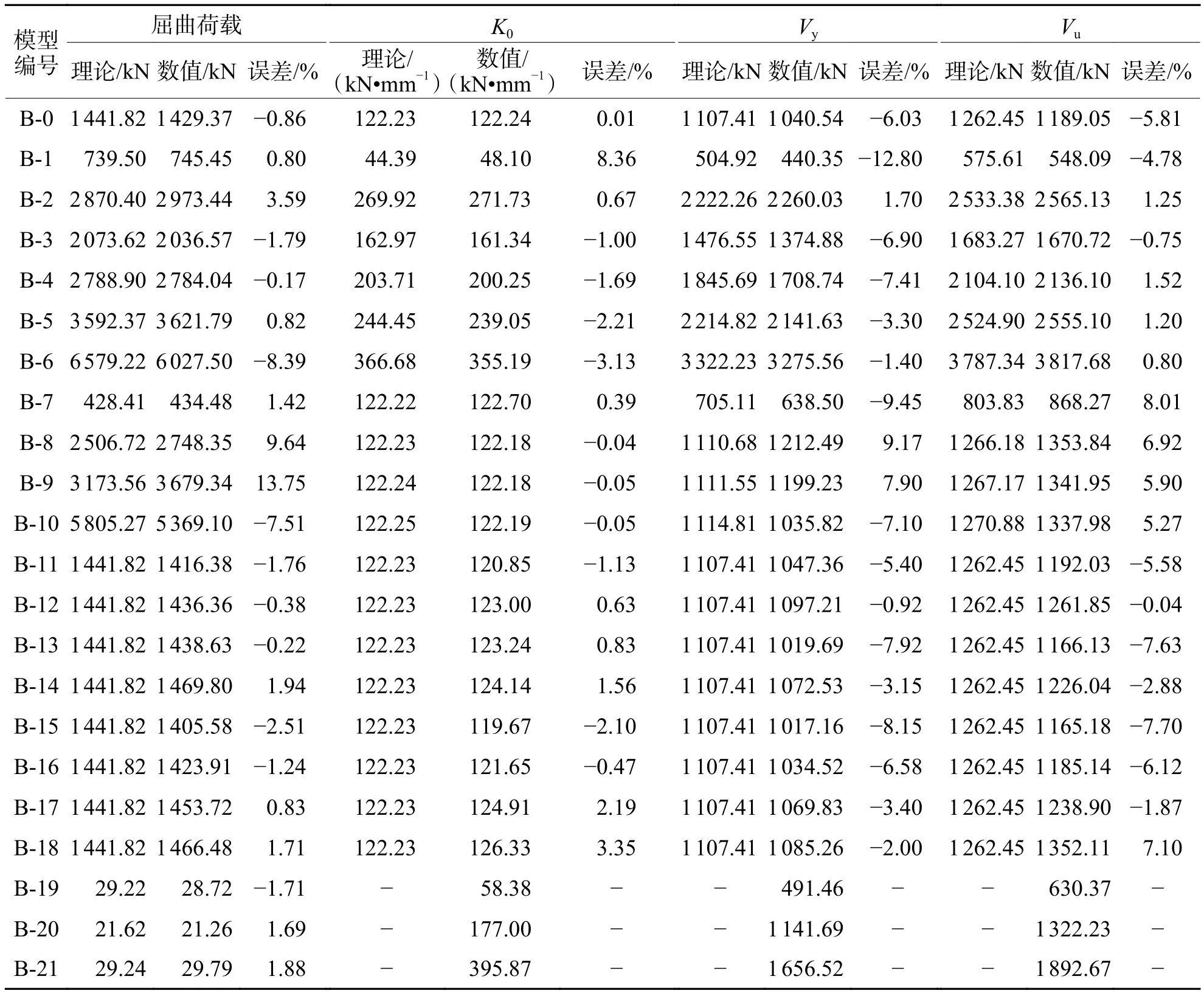
表1 理論公式的驗證Tab.1 Verification of theoretical formulas

對于彈性初始剛度，理論解與數值解的最大誤差為8.36%，此時對應于β=0.5.

由表1可知：當d＞30mm時，側邊加勁半圓形波紋鋼板墻屈曲荷載的理論解及數值解均高于屈服荷載，即側邊加勁半圓形波紋鋼板墻在側向荷載作用下先屈服后屈曲，表明半圓形波紋鋼板墻防屈曲性能優越；而平鋼板墻的屈曲荷載均遠小于屈服荷載，表明平鋼板墻在側向荷載作用下先屈曲后屈服；平鋼板墻的彈性初始剛度、屈服荷載及極限荷載均略大于半圓形波紋鋼板墻，這主要是由于豎向放置的半圓形波紋鋼板墻在側向荷載作用下的“風琴效應”引起.

4 側邊加勁半圓形波紋鋼板墻彈性屈曲

4.1 屈曲模態

對模型B-0～B-18施加單位水平荷載進行彈性屈曲分析，圖4為參數變化時側邊加勁半圓形波紋鋼板剪力墻的3種典型屈曲模態.

由圖4可知：

圖4 側邊加勁波紋鋼板墻的典型屈曲模態Fig.4 Typical buckling modes of CSPSW

1）在其他參數不變的情況下，隨著β的增大，B-0～B-2均發生整體屈曲，且屈曲波均發生在鋼板中心.

2）隨著λ的降低屈曲波的數量逐漸減少，且當λ≥500時，B-0及B-3～B-5發生整體屈曲，λ＜500時，B-6的加勁肋發生角部屈曲，這主要是由于當λ＜500時，隨著鋼板板厚的增加，加勁肋的厚度比愈來愈小，加勁肋對鋼板的約束不足，導致加勁肋先于鋼板屈曲，因此對于兩邊連接側邊加勁半圓形波紋鋼板墻，其加勁肋厚度比宜大于等于1.7.

3）改變波紋鋼板墻的圓形直徑d，B-0 及 B-7～B-9發生整體屈曲，且屈曲波的數量逐漸增多，B-10發生相關屈曲，為保證波紋鋼板墻在側向荷載作用下發生整體屈曲，其圓形直徑應滿足d＜120mm.

4）按加勁肋厚度不宜小于剪力墻鋼板厚度的要求，改變加勁肋寬厚比，在滿足規范規定bf≤27tf的情況下[21]，模型B-0及B-11～B-18均發生整體屈曲.

4.2 彈性屈曲臨界荷載

根據式（14）上，通過有限元計算結果擬合得到側邊加勁半圓形波紋鋼板剪力墻的彈性剪切屈曲臨界應力如式（15），ks取值如式（16）.

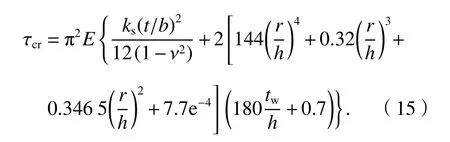
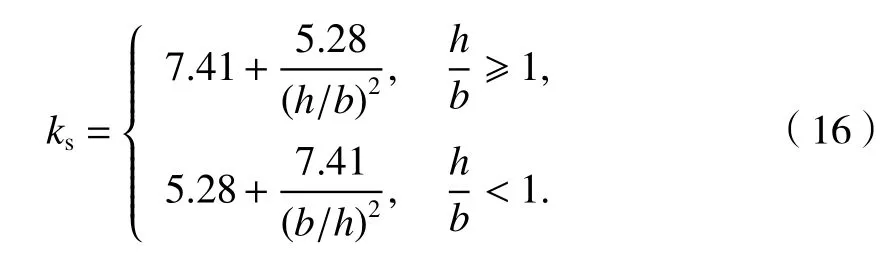
由彈性剪切屈曲臨界應力值即可計算得到彈性剪切屈曲臨界荷載Fcr為

由式（15）可看出，側邊加勁半圓形波紋鋼板墻的彈性剪切屈曲荷載可視為平鋼板墻彈性剪切屈曲荷載與波紋鋼板墻幾何形狀帶來剪切屈曲荷載增加的簡單疊加，其中波紋鋼板幾何形狀帶來的彈性剪切屈曲臨界應力的增加僅與鋼板墻的幅高比r/h和厚高比tw/h有關，且當r=0時，此部分值為0，式（15）退化為兩邊連接平鋼板剪力墻的彈性剪切屈曲荷載公式.

由式（15）計算得到的理論解與有限元模型得到的數值解對比結果如表1所示.理論解與數值解總體上吻合良好，模型B-9時的誤差13.75%為最大誤差，主要是由于圓弧直徑d=90mm的側邊加勁半圓形波紋鋼板墻的屈曲由整體屈曲向相關屈曲過渡，但此誤差仍滿足工程精度要求.

圖5為不同參數下彈性屈曲臨界荷載數值解的變化趨勢，由圖5可以看出：隨著高厚比的減小、跨高比及圓形直徑的增大，波紋鋼板墻的彈性屈曲臨界荷載呈線性增長，加勁肋肋寬從60 mm增至300 mm的變化過程中，其彈性屈曲荷載數值解與理論解的最大誤差為2.5%；tf＜3mm的情況下數值解與理論解差別很大，故在滿足規范加勁肋厚度不宜小于剪力墻鋼板厚度的規定下肋厚及肋寬對彈性屈曲臨界荷載影響很小，可以忽略，也驗證了式（15）中未考慮加勁肋肋寬的可行性；相較于圖5（f）所示平鋼板剪力墻B-19～B-21的彈性屈曲臨界荷載，側邊加勁半圓形波紋鋼板剪力墻的彈性屈曲臨界荷載有顯著提高.

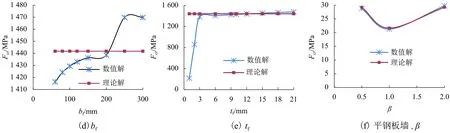
圖5 側邊加勁波紋鋼板墻彈性屈曲臨界荷載數值解與理論解對比Fig.5 Numerical solution and theoretical solution comparison of elastic buckling critical load on CSPSW

5 側邊加勁半圓形波紋鋼板墻破壞模式

由式（4）可知波紋鋼板墻在單位側向荷載作用下的彎曲變形、剪切變形主要與β及d相關，根據理論計算波紋鋼板墻不同參數時的剪切變形所占比例及有限元數值模擬結果分析，側邊加勁半圓形波紋鋼板墻的典型破壞模式有3種：

1）當β ＜1.0且3 0 mm≤d＜90mm時，波紋鋼板墻發生彎曲破壞，如圖6（a）所示；

2）當β ≥1.0且3 0 mm≤d＜90mm時，波紋鋼板墻發生彎剪破壞，如圖6（b）所示；

3）當β ≥1.0且d≥90mm或d＜30mm時，波紋鋼板墻破壞形式圖6（c），與圖6（d）所示平鋼板墻破壞形式相似，這是由于此時波紋鋼板墻發生局部屈曲，在側向荷載下相鄰波紋的面外變形逐漸合并形成了拉力帶形式的褶皺.

圖6 波紋鋼板墻的典型破壞模式Fig.6 Typical failure modes of CSPSW

6 結 論

1）提出一種新型側邊加勁半圓形波紋鋼板剪力墻，根據其簡化力學模型推導了彈性初始抗側剛度及承載力公式，并給出了彈性屈曲臨界荷載計算公式，通過數值分析驗證了理論公式的有效性.

2）波紋鋼板墻在d＜120mm及tf/tw≥1.7時，其屈曲模態均為整體屈曲；相同參數下，波紋鋼板墻的彈性屈曲臨界荷載及承載力均優于平鋼板剪力墻；隨著λ 的減小、β 及d的增大，波紋鋼板墻的彈性屈曲臨界荷載基本呈線性增長；參數bf及tf對波紋鋼板墻彈性屈曲臨界荷載的影響較小.

3）當d＞30mm時，側邊加勁半圓形波紋鋼板墻的屈曲荷載高于屈服荷載，即側邊加勁半圓形波紋鋼板墻在側向荷載作用下屈服先于屈曲，表明半圓形波紋鋼板墻優越的防屈曲性能.

4）當β ＜1.0且3 0 mm≤d＜90mm時，波紋鋼板墻發生彎曲破壞；當β ≥1.0且3 0 mm≤d＜90mm時，波紋鋼板墻發生彎剪破壞；當β ≥1.0且d≥90mm或d＜30mm時，波紋鋼板墻的破壞形式為拉力帶形式的“褶皺”.

致謝：廣州市高校“羊城學者”首席科學家（12015 41630）.