艦艇運動姿態實時預測方法研究

張 憶， 宋俊才， 李 坤

(中國船舶重工集團有限公司第七一○研究所，湖北 宜昌 443003)

艦艇在較高的海況條件下作戰時，艦艇上的武器發射裝置會隨著海浪的波動產生搖擺，這直接影響發射裝置發射角的精度，進而影響武器系統整體作戰效能的發揮。發射裝置在發射過程中，發射角的坐標與目標位置的坐標需要保持相對固定，所以需要對發射裝置進行穩定控制。穩定控制系統主要是通過姿態方位參考系統采集艦艇的運動姿態，控制系統對運動姿態數據進行處理和運算，輸出控制信號對發射裝置進行控制，從而保持發射裝置的相對穩定。在穩定控制系統中姿態方位參考系統采集姿態數據有一定的采樣周期，數據傳輸到穩定控制系統中需要傳輸時間，所以需要實時對艦艇的運動姿態數據進行預測。

艦艇運動姿態的預測主要采用自回歸(Autoregressive Model,AR)模型、灰色GM(1,1)預測模型、人工神經網絡方法、BP預測模型、極限學習機方法、長短記憶網絡、Volterra級數模型等方法[1-6]，大多數預測算法具有動態更新困難、預測效率差、算法復雜度高等特點，不能滿足本發射裝置穩定控制系統中對于實時預測的效率和計算需求。Kalman濾波是一種適用于實時計算的遞推線性最小方差濾波器，具有實時性高和計算復雜程度低的特點，可以用于實時預測艦艇的運動姿態。

本文基于Kalman濾波預測算法，提出了組合Kalman濾波隔點預測算法對艦艇的橫縱搖運動姿態進行實時預測，首先對組合Kalman濾波隔點預測算法進行了介紹，然后采用算法流程調整法、衰減記憶法和平方根法對預測算法改進優化，最后采用Matlab對優化前后的算法進行仿真實驗。通過對比分析仿真結果可知，改進優化的算法解決了運動姿態數據因采樣和傳輸產生的延遲問題，滿足發射裝置對艦艇姿態實時預測的需求。

1 組合Kalman濾波隔點預測算法

1.1 組合Kalman隔點預測法原理

姿態方位參考系統測量的艦艇運動姿態數據需要傳輸給控制系統，其中數據采集和數據傳輸存在時間延遲，因此需要將應用當前采集數據預測下一點采集數據的Kalman濾波預測法修改為預測第2點采集數據的方法，即Kalman隔點預測法[7]。將兩個Kalman隔點預測法組合起來，稱為組合Kalman隔點預測法，其預測周期Tt為數據采樣周期的2倍。以數據前面的4個點為已知采樣數據，組合Kalman濾波隔點預測算法的原理如圖1所示。

圖1 組合Kalman濾波隔點預測算法的原理圖

1.2 Kalman濾波預測算法

艦艇運動姿態的狀態方程和量測方程為[8-13]

X(t)=AX(t-1)+BU(t-1)+W(t-1)

(1)

Z(t)=HX(t)+V(t)

(2)

式中，X(t)為艦艇t時刻的運動狀態；A為狀態轉移陣，將t-1時刻狀態和t時刻狀態聯系起來；X(t-1)為艦艇t-1時刻的運動狀態；B為艦艇姿態控制輸入U(t-1)的增益矩陣；U(t-1)為t-1時刻可選的艦艇姿態控制輸入；W(t-1)為艦艇姿態輸入高斯白噪聲，為零均值、方差陣為Q的不相關白噪聲；Z(t)為對艦艇運動姿態的測量信號；H為測量矩陣，表示狀態變量X(t)對測量變量Z(t)的增益；V(t)為測量噪聲，為零均值、方差陣為R的不相關白噪聲。

預測估計的公式為

(3)

(4)

濾波增益矩陣的公式為

(5)

式中，Kg(t)為t時刻艦艇姿態的濾波增益矩陣；HT為測量矩陣的轉置；R為測量噪聲的方差。

濾波估計的公式為

(6)

(7)

式中，Xt為t時刻艦艇姿態的濾波估計值;Pt為t時刻艦艇姿態的濾波誤差協方差矩陣;I為單位矩陣。

本研究中假設在艦艇沒有控制輸入的情況下對運動姿態進行實時預測，式(3)變為

(8)

根據上述Kalman濾波公式的描述，可得到Kalman濾波預測流程,如圖2所示。

圖2 Kalman濾波預測流程圖

2 組合Kalman濾波隔點預測算法優化

對組合Kalman濾波隔點預測算法進行分析，其算法是先輸出預測值，之后加入測量值計算估計值，預測值與測量值間存在滯后；實際的控制系統不能得到準確的艦艇運動姿態模型，導致預測算法中的新測量值對預測值的修正作用下降，舊測量值的修正作用相對上升；預測算法在計算過程中存在舍入誤差積累，可能導致計算發散。基于以上原因，需要采用算法流程調整法、衰減記憶法和平方根法對預測算法進行改進優化。

2.1 算法流程調整法

采用算法流程調整法解決預測值與測量值間存在滯后的問題，調整組合Kalman濾波隔點預測算法的計算流程，先對艦艇姿態的濾波增益矩陣和濾波估計的公式進行計算，然后對預測估計的公式進行計算。則式(4)～式(8)調整為

Kg(t)=Pt-1HT/(HPt-1HT+R)

(9)

Xt=Xt-1+Kg(t)(Zt-HXt-1)

(10)

Pt=(I-Kg(t)H)Pt-1

(11)

(12)

(13)

調整后的Kalman濾波預測流程如圖3所示。

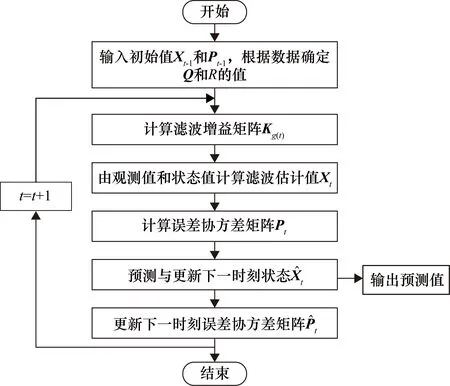
圖3 調整后的Kalman濾波預測流程圖

2.2 衰減記憶法

針對預測算法中的新測量值對預測值的修正作用下降、舊測量值的修正作用相對上升的問題，采用衰減記憶法予以解決。實際運用中采用的衰減記憶法通過逐漸減小舊測量值的權重，同時增加新測量值的權重[14]來實現。與組合Kalman濾波隔點預測算法方程相比，衰減記憶法的不同之處在于艦艇姿態的預測誤差協方差矩陣的計算公式(式(13))中多了一個標量因子s，即

(14)

式中，s為標量因子。

2.3 平方根法

組合Kalman濾波隔點預測算法在計算過程中的舍入誤差積累會導致Pt-1和Pt喪失非負定性，Pt-1和Pt的非負定性將使Kg(t)的計算失真，從殘差中提取的補償信息越來越不準確，最后造成計算發散。采用平方根法解決計算發散的問題，在計算過程中不是計算Pt-1和Pt，而是計算Pt-1和Pt的平方根，從而抑制計算發散[15]。

由矩陣理論可知，任意非零矩陣Ln×m與其轉置矩陣LT的乘積是非負定的，L稱為矩陣的平方根。進行平方根計算時采用喬萊斯基(Cholesky)分解法對誤差協方差矩陣進行下三角分解。

設非負定陣P3×3為

(15)

式中，Pij為非負定陣P的元素。

設P的下三角分解矩陣Δ和其轉置矩陣ΔT為

(16)

(17)

P=Δ×ΔT

(18)

式中，δij為非負定陣Δ的元素；Δ為P的下三角分解矩陣；ΔT為矩陣Δ的轉置矩陣。

將式(9)和式(11)調整為

(19)

(20)

綜上所述，改進優化后的組合Kalman濾波隔點預測算法與改進優化前的算法相比，具有如下優點：① 前者改變了算法的計算流程，先對艦艇姿態的濾波增益矩陣和濾波估計的公式進行計算，然后對預測估計的公式進行計算；② 前者在預測誤差協方差矩陣的計算式子中添加了一個標量因子s；③ 前者對Pt-1和Pt進行下三角分解，運用矩陣的平方根參與計算。改進優化算法可以提高預測算法的預測精度，增加新測量值對預測值的修正作用，同時抑制預測算法在計算過程中的計算發散；其比改進優化前的算法更符合實際運用的需求，更能滿足穩定控制系統對艦艇運動姿態預測值的需要。

3 仿真實驗

3.1 仿真數據模型

本文以姿態方位參考系統測量的艦艇近海橫搖數據為仿真原始數據，數據的采樣周期T為0.5 s，共有480個橫搖數據。前40個橫搖數據如表1所示。

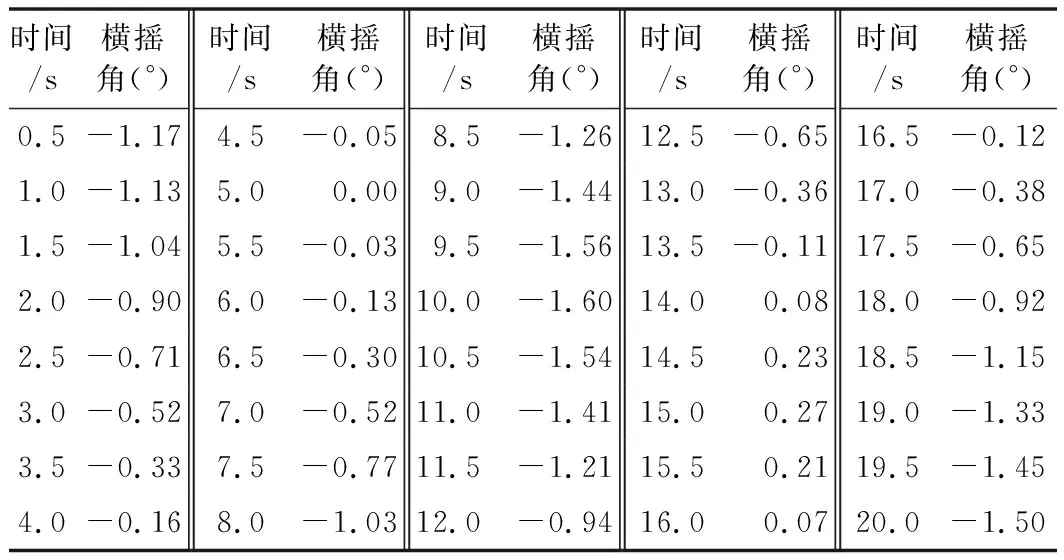
表1 前40個橫搖數據表

3.2 初始值和參數輸入

艦艇的橫搖數據是通過姿態方位參考系統測量得到的解耦數據，其橫搖運動為非線性的，為了簡化運動模型，假設艦艇橫搖兩點之間做等加速直線運動，并通過實時更新橫搖角度、角速度和角加速度減小非線性對預測精度的影響。由等加速直線運動的運動規律可以得到狀態方程的公式為

(21)

式中，T為數據的采樣周期。

所以，可以得到狀態轉移陣A為

(22)

根據橫搖數據前3個點可以得到初始角度、初始角速度和初始角加速度，其共同組成了初始值矩陣Xt-1；組合Kalman濾波隔點預測算法的預測步長Tt為1 s；初始矩陣Pt-1的元素取任意假定的非零值，本文中取值如式(23)所示；查閱資料可以得到，在工程實際中艦艇姿態輸入高斯白噪聲的方差陣Q一般取單位矩陣，如式(24)所示，方差陣Q中的元素值增大，預測算法的均方根誤差減小；測量噪聲的方差R是根據姿態方位參考系統的型號和技術指標，其測量橫縱搖的誤差為0.1°，R確定為0.01，方差R增大，預測算法的均方根誤差增大；由姿態方位參考系統得到的數據為艦艇橫搖角度位置，所以測量矩陣H為式(25)。在仿真實驗中，測量值直接讀取對應時刻的480個橫搖數據，衰減記憶濾波的標量因子s在仿真中確定為100。

(23)

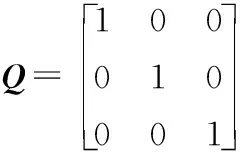
(24)

H=[1 0 0]

(25)

3.3 仿真結果

根據初始值和參數的輸入，采用Matlab對組合Kalman濾波隔點預測算法和優化后的組合Kalman濾波隔點預測算法進行仿真，仿真結果如圖4和5圖所示。

圖4 橫搖角度預測結果圖

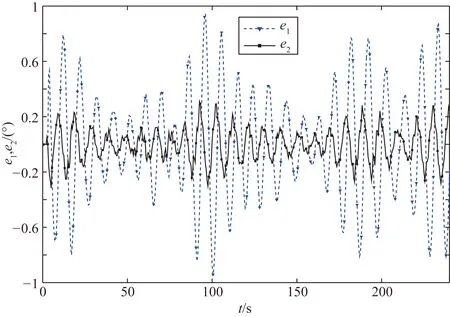
圖5 橫搖角度預測誤差圖

圖4中，實線S為姿態方位參考系統測量的近海艦艇橫搖數據，點線S1為組合Kalman濾波隔點預測算法預測的數據，點畫線S2為優化后組合Kalman濾波隔點預測算法預測的數據。從圖4的仿真結果可以分析，組合Kalman濾波隔點預測算法的預測數據與測量數據相比，存在數據滯后，優化后預測算法的預測數據滯后情況得到明顯改善。

圖5中，點線e1為組合Kalman濾波隔點預測算法預測數據與測量數據的誤差，實線e2為優化后組合Kalman濾波隔點預測算法預測數據與測量數據的誤差。從圖5的仿真結果可以分析，優化后預測算法預測數據的誤差比優化前預測數據的誤差要小。

優化后的預測算法與優化前的算法相比，前者主要在采用平方根法對矩陣Pt-1和Pt計算時增加了計算量，根據仿真計算的時間估計，優化后的預測算法增加的計算量可以忽略不計。分別對兩種算法的橫搖角度預測誤差求均方根，組合Kalman濾波隔點預測算法的均方根誤差為0.3935°，優化后組合Kalman濾波隔點預測算法的均方根誤差為0.1173°。優化后的預測算法的均方根誤差比原算法減小0.2762°，根據穩定控制系統對運動姿態實時預測的精度要求，其均方根誤差需要小于0.2°，優化后的預測算法滿足姿態數據實時預測的需求。

4 結束語

本文提出了組合Kalman濾波隔點預測算法對艦艇的運動姿態數據進行預測，針對預測算法存在的預測值與測量值滯后、新測量值對預測值的修正作用下降和計算發散的問題，采用算法流程調整法、衰減記憶法和平方根法對預測算法進行改進優化。依據姿態方位參考系統測量的近海艦艇橫搖數據，輸入實際發射裝置穩定控制系統的參數，采用Matlab軟件對優化前后的預測算法進行仿真實驗。通過將仿真結果與測量數據進行對比計算可知，改進優化后的預測算法的均方根誤差小于0.2°，滿足艦艇姿態數據實時預測的需求。后續將會把預測算法運用到實際艦艇上的發射裝置穩定控制系統中，達到預測姿態數據的目的。