FCS-MPC在HAPF無功補償控制中抑制諧振的研究

汪玉鳳， 張紅梅， 殷煜煒

(遼寧工程技術大學 電氣與控制工程學院，遼寧 葫蘆島 125105)

在輸配電系統中，無功電流的動態變化會引起電壓調節和穩定性被破壞的問題，使電能質量惡化，并增加系統損耗。為了解決與高可變無功功率負載相關的問題，使用有源補償器(如靜止同步補償器(STATCOM)、UPFC統一潮流控制器(UPFC)、有源電力濾波器和混合濾波器)要優于電容器組[1]。一般來說，混合濾波器的控制由兩種算法組成：一種是負載無功功率，另一種是負載控制設備根據負載需求提供的無功功率。對于混合濾波器中的輸出控制策略，最常見的算法是將PI控制器用于d-q參考系或滯環控制器[2]。近年來，自適應控制、滑模控制和預測控制等控制策略的使用越來越廣泛[3-5]。在各種預測控制器中，有限控制集模型預測控制(Finite Control Set Model Predictive Control，FCS-MPC)在電力電子領域已成為研究的熱點。FCS-MPC考慮了有限數量的開關狀態，以限制控制動作的數量。FCS-MPC采用離散的數學模型來預測系統在每一開關狀態下的狀態。最后，為了解決優化問題，建立了成本函數對預測值進行評估，以確定控制狀態。

已經有部分文獻研究了幾種用于識別負載無功功率的技術。文獻[6]～文獻[8]闡述了幾種用于識別負載無功功率的技術，包括SRF(Self Resonant Frequency,自諧振頻率)[6]、p-q理論[7]以及基于小波和自適應濾波等[8]。文獻[9]～文獻[11]為彌補轉換器模型的簡單性，提出了FCS-MPC廣泛應用于與L濾波器并聯的轉換器。例如，文獻[9]在使用STATCOM進行無功補償時，使用FCS-MPC通過解耦有功和無功控制改善了設備的動態響應。然而，FCS-MPC在無功功率控制混合濾波器中的研究比較少。文獻[11]提出了FCS-MPC在LCL濾波器的并網變換器中的應用，由于算法固有的可變開關頻率，所以會稍微復雜一些。 除了諧振外，電容器在濾波器的模型方程中引入了延遲，這使線電流的直接控制變得復雜。 然而，由于算法的優勢，在開關頻率可變的LCL濾波器的穩定性和諧振問題上，FCS-MPC的應用具有一定的意義。文獻[11]～文獻[13]針對多變量控制和長時間預測等問題，提出了幾種將控制技術與有源阻尼算法相結合的解決方案。

綜上所述，筆者利用FCS-MPC的主要優點來改善HAPF(Hybrid Active Power Filter，混合有功電力濾波器)的動態無功功率控制。使用基于LCL濾波器方程的離散模型來預測系統狀態并優化成本函數。將所提出的控制技術與有源阻尼算法結合起來。采用自適應陷波器(Adaptive Notch Filter，ANF)的簡單結構來實現有源阻尼算法，并獲得控制參考和負載反饋功率。使用ANF的方法與SRF相比不僅減少了控制算法的處理時間，而且改善了動態響應。本文提出的控制策略提高了設備的動態響應、有功和無功功率控制之間的解耦能力和正確跟蹤無功功率參考波動的能力。為了證明控制算法的有效性，在一個7.5 kVA的單相HAPF模型上進行了仿真和實驗。

1 FCS-MPC混合型有源電力濾波器的建模與分析

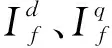
圖1 HAPF拓撲無功補償

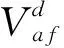
VS=Vaf-j(XC)If

(1)

(2)

(3)

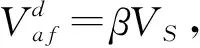
(4)

FCS-MPC的使用前提是HAPF模型必須將變頻器電壓(Vinv)定義為輸入，并將混合濾波器電流(If)定義為輸出。

如圖2所示，為混合有源電力濾波器標幺值等效電路，該模型表示了每單位(p.u.)的變量，Vinvpu和Iinvpu分別為逆變器的單位電壓和電流。LCL濾波器參數為：Lfpu和Rfpu(逆變器側濾波器電感及其內阻)；Cfpu和Rcfpu(濾波器并聯電容及其內阻)；Rtpu和Ltpu(短路變壓器電阻和電感)。

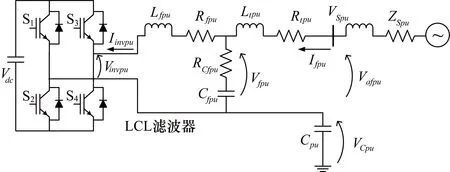
圖2 混合有源電力濾波器標幺值等效電路

此外，Vfpu為濾波電容器的電壓；Ifpu為混合濾波器電流；Vafpu為有源濾波器電壓；VCpu為電容器組電壓；VSpu為源電壓。用標幺值表示使得空間狀態建模更容易，考慮到變頻器是通過耦合變壓器連接到系統。HAPF的狀態空間方程表示為

x(t)=Ax(t)+Bu(t)

(5)

為了表示混合濾波器的動態性能Iinvpu、Ifpu和Vfpu被定義為狀態變量，Vinvpu和Vafpu被定義為控制變量。

(6)

其中,

(7)

狀態空間連續系統可以被有效地離散化，如式(8)～式(10)所示：

x(k+1)=Adx(k)+Bdu(k)

(8)

Ad=eATs≈I+ATs

(9)

Bd≈BTs

(10)

式中，k為采樣周期(t=kTs)的倍數；Ad為離散狀態矩陣；Bd為離散輸入矩陣。

2 有限控制集模型預測控制

FCS-MPC通過電子變換器的離散特性來減少MPC算法的計算次數。逆變器具有有限數量的開關狀態，因此僅針對該操作集來解決優化問題。先前提出的HAPF的離散模型用于預測下一個采樣時刻xP(k+1)的狀態變量。在本文中，使用的逆變器是一種單相H橋，常用于分布式發電系統。對于單相逆變器，算法必須考慮4個開關狀(Sn)：v0=0,v1=Vdc,v2=-Vdc,v3=0。采用的控制方法考慮到參考狀態空間變量(x*)和每個開關狀態(xP)的預測值來估計定義的成本函數J=|x*-xP|。因此，最小化成本函數的Sn作為下一個采樣周期的控制動作時，預測范圍是N=2，為了補償由處理時間引起的延遲，首先估計xP(k+1)的值，然后評估xP(k+2)的代價函數[14]。

如圖3所示，表示了應用于HAPF的FCS-MPC控制策略，步驟如下：

① 測量狀態變量：Vf，Iinv，If，Vs，IL，Vdc。

② 應用最佳開關狀態Sopt。

③ 獲得系統變量的p.u.值。

⑥ 將有效阻尼項添加到Vfpu。

⑦ 從式(8)估計(k+1)時刻的系統狀態。

⑧ 預測(k+2)時刻的系統狀態。

⑨ 評估成本函數以定義最佳切換狀態(Sopt)并在下一次采樣中應用。

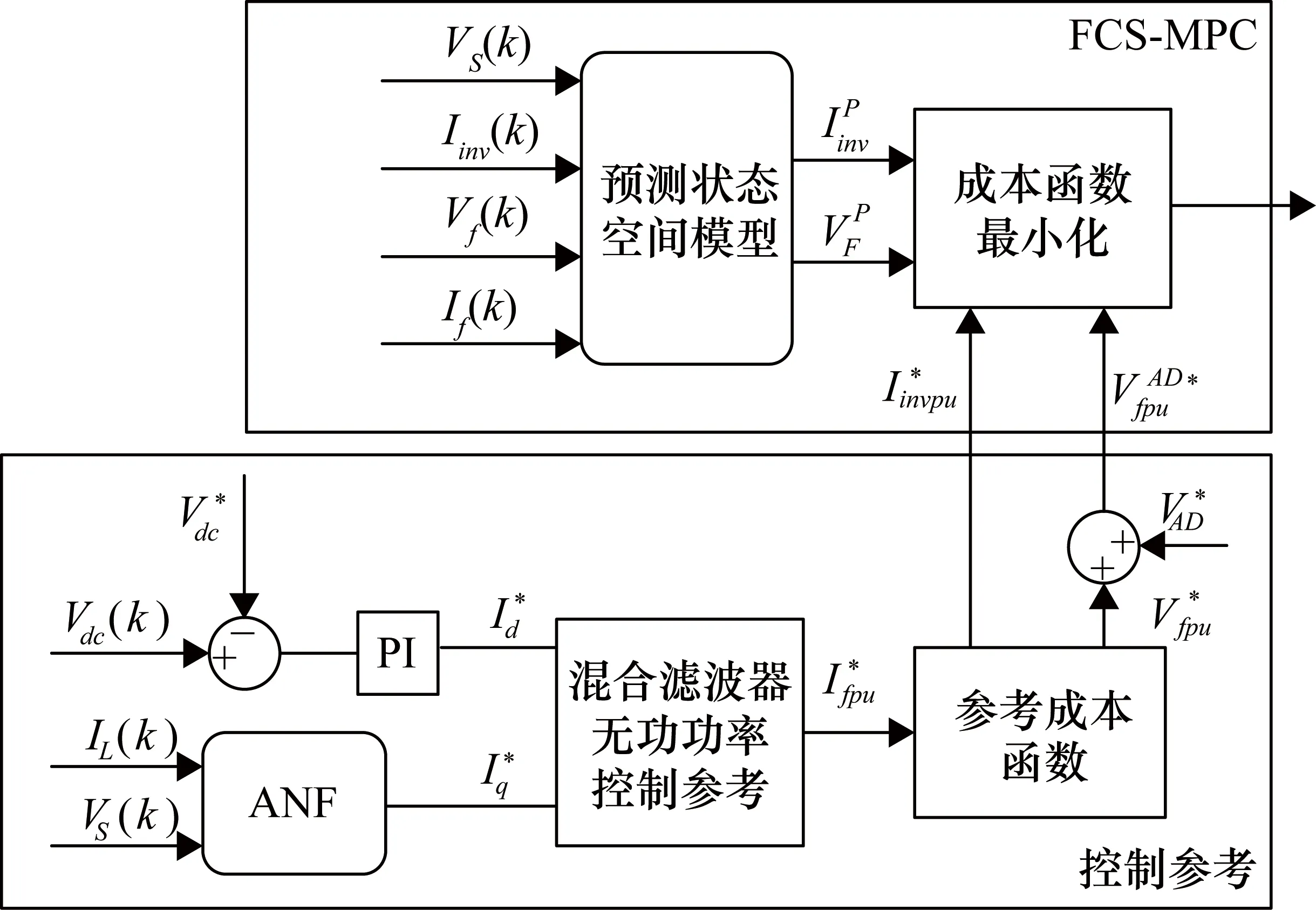
圖3 混合濾波器FCS-MPC框圖

2.1 自適應陷波濾波器設計

FCS-MPC控制LCL濾波器所構成的逆變器需要使用額外的算法來避免不需要的共振，本文應用一個自適應陷波濾波器進行有源阻尼并獲得FCS-MPC的控制參考。如圖4所示，給出了ANF結構[14]，d(k)為輸入信號，y(k)為輸出信號，誤差e(k)用于自適應法則。這個濾波器的目的是保證y(k)可以在幅度和相位上跟蹤基頻輸入信號。使用最小均方(Least Mean Square，LMS)算法來調整系數，雖然LMS是自適應濾波中最簡單的算法，但它對諧波提取的響應與遞歸最小二乘算法相似[15]。

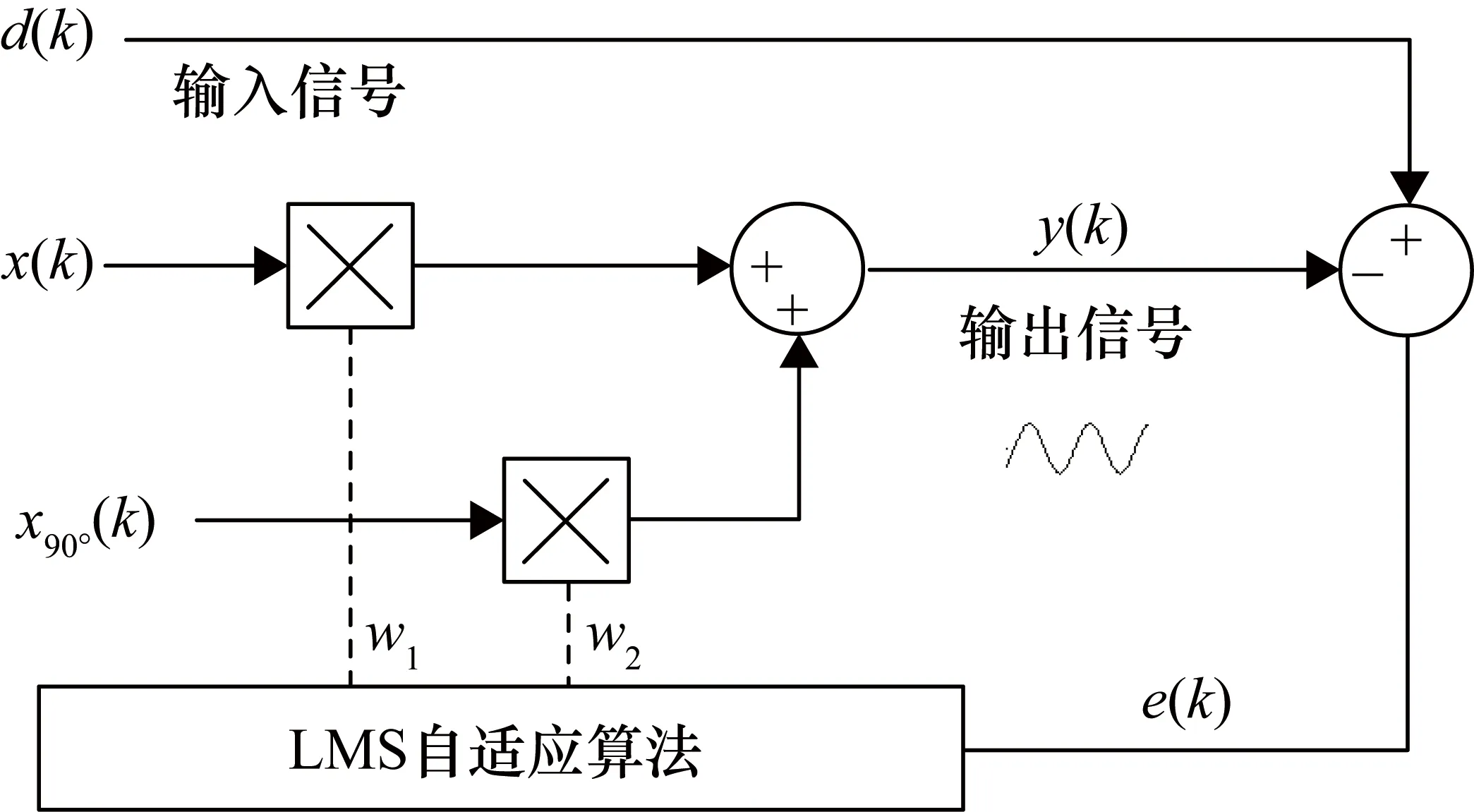
圖4 自適應濾波原理

式(11)～式(13)給出了用于ANF的LMS算法的一般遞歸公式：

y(k)=w1(k)x(k)+w2(k)x90°(k)

(11)

e(k)=d(k)-y(k)

(12)

w1(k+1)=w1(k)+μe(k)x(k)

(13)

w2(k+1)=w2(k)+μe(k)x90°(k)

(14)

式中，x(k)和x90°(k)為由數字PLL(鎖相環)提供的兩個正交信號；w1(k)和w2(k)為濾波器系數；μ為步長值，用于控制算法的收斂速度及其精度。ANF只有兩個系數需要調整，這使得ANF控制算法比其他算法顯得更容易且更快[14]。考慮ANF的輸出時，它的基本組成部分為

y(k)=w1(k)sin(ωt)+w2(k)cos(ωt)

(15)

式(15)可化簡為

y(k)=asin(ωt+θ)

(16)

式中，a為峰值；θ為參考信號和輸出信號之間的角度。 擴展這個等式的結果為

y(k)=acosθsin(ωt)+asinθcos(ωt)

=w1(k)sin(ωt)+w2(k)cos(ωt)

(17)

ANF系數w1(k)和w2(k)分別等同于SRF中的dq分量。如文獻[16]所述，與SRF相比，ANF具有更好的動態響應并且所用的處理時間更短。通過采用單位輸入正交信號，可以在0<μ<0.5的范圍內確保步長值的穩定性[17]。

2.2 混合濾波器的控制參考量

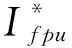
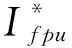
(18)

式中，sin(ωt)和cos(ωt)由PLL提供且與電源電壓相位相同。

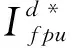
(19)

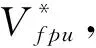
(20)

(21)

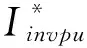
(22)

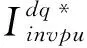
(23)

在時域中，電流由下面公式給出：

(24)

2.3 有源阻尼設計和諧波抑制算法

合理的LCL濾波器設計可有效避免諧振。本文所設計的LCL濾波器采用了文獻[14]中提出的一些概念和可用的無源元件，并在其基礎上，引入了兩個諧振頻率fr1=1448 Hz和fr2=1574 Hz。由于FCS-MPC的可變開關頻率，因此有必要采用阻尼諧振技術來確保控制的穩定性；使用與輸出電感串聯的虛擬電阻(RV) 來滿足所需的阻尼諧振以及避免由電源電壓失真引起的諧波電流，為了利用這兩個特性，用ANF來模擬這種電阻對諧波頻率的影響。表1給出了所獲取的數值。有源阻尼策略的結構圖，如圖5所示。

表1 LCL濾波器參數

圖5 有源阻尼策略的結構圖

2.4 LCL電容器電壓和逆變器電流的變量控制

FCS-MPC通過適當定義成本函數可以同時控制Vf和Iinv。當3個狀態變量中的兩個被控制時，更易于確保穩定性且避免了諧振。Iinv控制保證了穩定性，Vf控制允許有效的主動諧振阻尼和源電壓諧波抑制。多變量成本函數為

(25)

式中，Kinv和Kf為定義控制優先權的成本函數收益。 由于系統以標幺值表示，因此不需要對成本函數變量進行歸一化。

3 仿真與實驗

在Matlab/Simulink中進行仿真，并對所提出的FCS-MPC算法進行實現和評估。表1中列出了LCL濾波器參數，采樣頻率為40 kHz。系統參數設計如表2所示。

表2 系統參數

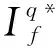
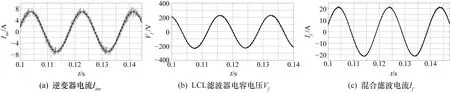
圖6 多變量控制的狀態變量及其參考值

成本函數通過保持Kinv=1增加Kv來優先控制Vf。當Kv=0時，系統只控制Iinv，Vf呈現出明顯的直流電壓水平。

成本函數增益如圖7所示。其中，圖7(a)顯示了Kv增加時的直流電壓分量特性。當Kv>30時，直流分量被消除。由于電壓參考(Vf直流分量)中加入的項與諧波電流成比例，所以它也影響有源阻尼。圖7(b)顯示了不同Kv和Rv值時的混合濾波器電流THD(Total Harmonic Distortion，總諧波畸變)。由于ANF用于隔離諧波電流，因此Rv和Kv的值太高的話會影響FCS-MPC的動態特性。盡管ANF具有一定的動態響應能力，但仍然比FCS-MPC響應慢得多。為此，基于仿真結果選擇Kinv=1，Kv=80和Rv=40，以保證If的THD值較低，對算法的動態響應沒有明顯影響。仿真證明了FCS-MPC用于HAPF無功功率控制的可行性，并且評估了多個工作點控制參數和成本函數增益。

圖7 成本函數增益

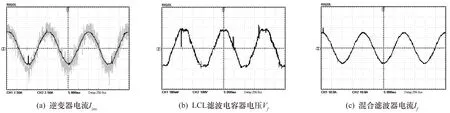
圖8 FCS-MPC的穩態性能

混合濾波器電流If和有源阻尼(Active Damping，AD)的瞬態響應如圖9所示。

圖9 混合濾波器電流If和有源阻尼(AD)的瞬態響應

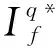
圖10 電流波動軌跡

圖10(a)表明，由于直流母線電壓波動，PI控制器不能對有功和無功功率進行解耦。因此，它不能適應當前的參考電流。另外，FCS-MPC能解耦有功和無功潮流(恒定的直流母線電壓)，并能精確跟蹤電流基準的波動。

HAPF的動態負載參考如圖11所示。利用具有平滑直流電抗器的3 kVA單相晶閘管整流器驗證了用于非線性負載無功補償的FCS-MPC算法。首先，調整觸發角度α，當α≈60°時，調整角度后，負載所需的無功功率為1850 Var，THD為32.6%。負載階躍后，當α2≈10°，負載無功功率為680 Var，THD為33.8%。HAPF可以確保電源端的無功功率和THD的混合濾波器電流均小于5%，這說明了諧波抑制算法的有效性。 因此，FCS-MPC算法可以實現快速補償，以避免電壓波動使線路電流最小，并精確地跟蹤負載無功功率。結果表明，HAPF可以有效跟蹤非線性負載瞬時狀態，需要時間大約為12.1 ms，遠小于1個周期，控制時間上遠小于其他文獻中提出的HAPF控制策略。例如文獻[18]提出了一種基于改進的拓撲結構的SRF比例諧振電流控制，在約等于2.5個周期時才達到穩態；文獻[1]提出的基于新型混合有源濾波器拓撲的比例諧振控制器在約等于1.5個周期內達到穩態。因此，提出的基于FCS-HAPF的控制方法的動態響應和跟蹤負載變化相比于其他方法快得多。 這一優點使得該控制策略可以用于需要快速無功補償的系統，如電弧爐、焊接系統和風力發電場等，且補償效果更好。

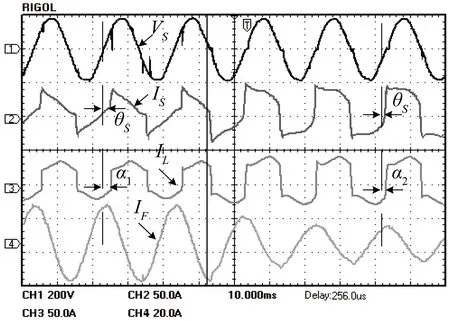
圖11 HAPF的動態負載參考

4 結束語

本文詳細研究了FCS-MPC在混合有源電力濾波器中的應用。該算法能夠控制HAPF無功功率，改善其動態響應。仿真和實驗結果表明，FCS-MPC用于HAPF無功功率控制的可行性。并且評估了多個工作點的控制參數和成本函數增益，獲得的結果是相似的。多變量成本函數適用于控制由LCL濾波器構成的HAPF；驗證了ANF算法對阻尼諧振的抑制能力，并且阻斷了電源電壓失真引起的諧波。保證了混合濾波器在穩定狀態下的電流THD能達到標準值。該策略與傳統的PI控制器相比，提高了設備的動態響應能力、有功和無功功率控制之間的解耦能力和正確跟蹤無功功率參考波動的能力。