一種自動化并行重疊網格隱式裝配方法

郭永恒，江雄，肖中云，王子維，盧風順

中國空氣動力研究與發展中心 計算空氣動力研究所，綿陽 621000

隨著大規模并行計算技術的不斷進步，計算流體力學(CFD)能夠處理的非定常數值模擬問題更加豐富[1]；對多體相對運動的情形，比如共軸雙旋翼直升機的氣動干擾[2-3]、超聲速子母彈的播撒[4]、運載火箭低空大動壓頭罩分離[5]、水陸兩棲飛機靜水滑行[6]、外掛式導彈的發射[7]等，單純的結構或非結構網格已不能滿足分析需求。憑借較高的靈活性，重疊網格裝配已發展成為處理上述問題的關鍵技術之一。

重疊網格裝配有顯式與隱式兩類方法。在網格生成階段，顯式方法[8]需要在固壁附近構造出挖洞邊界以輔助劃分單元類型，同時還要人工指定多組部件網格的重疊關系矩陣，從而導致裝配自動化水平偏低，難以適應網格運動時的分析需求。相比之下，隱式方法摒棄了人工洞邊界，結合網格拓撲結構以及網格組之間的度量關系進行幾何計算，能夠極大地提升重疊裝配的自動化水平。然而，在隱式裝配方法并行化過程中，當網格規模和重疊區域增大時，算法涉及的查詢運算量和進程間的通信壓力急劇攀升，成為制約隱式裝配技術工程應用的瓶頸問題[9]。

為了提高重疊網格隱式裝配效率、拓展其工程應用范圍，大量專業化的重疊分析軟件得以發展起來。Overflow[10]與Beggar[11]是基于重疊網格的流場模擬軟件，已在工程實踐中得到廣泛應用，但其重疊分析模塊與流場求解器緊密耦合，難以被第三方求解器使用。PEGASUS[12]能夠并行裝配運動部件網格，但其分析結果只能通過計算機文件系統進行傳輸，且大量參數的人工控制導致其自動化水平較低。SUGGAR裝配軟件與插值工具庫DiRTlib結合[13]能夠很好地解決結構/非結構重疊網格的裝配問題，并且可以嵌入到多種流場解算器中；但進行復雜構型網格挖洞時，控制參數需要經大量嘗試才能達到合適的水平。SUGGAR++[14]在自動化程度、魯棒性以及效率方面有了較大改進，但是其直接挖洞算法無法適應幾何構型不封閉的情況。重疊網格裝配中間件TIOGA[15]將快速搜索算法和動態負載平衡技術相結合，大幅提升了重疊網格的并行裝配效率；但算法的內在屬性導致隱式挖洞邊界光滑性欠佳，進而影響流動模擬品質的提升。

綜合來看，常見的重疊網格隱式裝配方法皆起源于Lee和Baeder提出的壁面距離準則[16-17]。在其并行化實現過程中，當前部件網格節點到自身所屬壁面距離的計算、當前部件網格節點到其他部件壁面距離的插值以及貢獻單元的存在性判斷共同構成了隱式裝配的自動挖洞過程。正是上述3個步驟的高度耦合使幾何分析過程呈現出復雜和低效性質，初始階段節點無差別查找操作影響并行裝配效率。

針對上述問題，本文根據壁面距離準則，構造出一種高度自動化的重疊網格隱式裝配方法，其基本思路是：首先，結合協方差分析、切割盒子等快速算法，將壁面距離計算與貢獻單元存在性判斷解耦，實現網格組動態重疊關系的自動化識別；其次，結合集合分析，設計出并行化的自動挖洞算法；最后，通過快速查詢方法建立重疊單元與貢獻單元的插值關系。其中，第1節使用集合論語言對重疊網格隱式裝配算法進行描述；第2節詳細介紹算法的并行實現細節，包括提升效率和自動化水平的各種關鍵技術；第3節使用多部件重疊的網格模型測試算法的并行效率，并結合流場解算器測試重疊插值結果的準確性；最后給出結論與展望。

1 重疊網格隱式裝配算法的集合論表示

現有的重疊網格隱式裝配方法都是依據“網格節點到固體壁面的距離”進行構造的[18]，但是在實現過程中，流場計算單元、重疊插值單元以及洞內單元的劃分準則具有很大的差異；例如，很多研究者[18-20]根據網格圖形范例進行算法描述。對于復雜幾何構型、多部件網格重疊、部件網格外緣邊界與挖洞邊界相交等復雜情形，圖示法的嚴謹性便顯得不夠充分。因此，需要使用集合論語言對重疊網格隱式裝配原理進行嚴格地描述。

設整個求解域上包含M個部件的集合為CompSet，對于任意部件compi∈CompSet都存在網格組gpi與之構成一一對應關系，其中i∈{1,2,…,M}。設網格組gpi的節點集合、面單元集合、體單元集合依次為NodeSeti、FaceElemSeti及VolElemSeti，那么根據計算流體力學通用符號系統(CFD General Notation System, CGNS)定義的拓撲結構，三者之間建立起空間鏈接關系；設固壁邊界面上的網格節點集合為SolidNodeSeti，它與NodeSeti的關系為

SolidNodeSeti?NodeSeti

(1)

1.1 網格組節點集合劃分

任取一個網格節點P∈NodeSeti，設它到第j個部件壁面的距離為

d(P,SolidNodeSetj):=

MinVal{d(P,Q)|Q∈SolidNodeSetj}

(2)

特別地，當i=j時，d(P,SolidNodeSetj)是節點到自身網格組壁面的距離。如果存在一個網格組gpj(j≠i)同時滿足如下條件：

(3)

每個網格組節點集合NodeSeti都被劃分成活躍節點集合PosNodeSeti與非活躍節點集合NegNodeSeti，即

NodeSeti=PosNodeSeti∪NegNodeSeti

(4)

當網格節點集合完成式(4)的分類后，便得到重疊網格的挖洞邊界。通過拓展挖洞邊界處的體單元，即可實現洞內單元、重疊單元以及場單元的自動識別。

1.2 網格組單元劃分

每個網格組gpi的單元劃分包括4個步驟(在不引起歧義的情況下，文中的集合符號均省略下標i)：

1) 在部件網格組gp上，由于與延拓型物理邊界面相鄰的體單元不可能在計算過程中扮演場單元的角色，進而也不可能成為其他網格組上重疊單元對應的貢獻單元，因此VolElemSet可劃分為一般單元集合GeneralElemSet與延拓型單元集合ExtendElemSet，即

VolElemSet=GeneralElemSet∪ExtendElemSet

(5)

2) 如果體單元velem∈VolElemSet的所有節點皆為非活躍點集合NegNodeSet中的元素，那么定義velem為非活躍單元。如果體單元

velem∈GeneralElemSet=VolElemSet∩

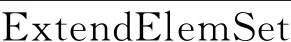
(6)

的所有節點皆為活躍點集合PosNodeSet中的元素，那么定義velem為活躍單元，否則定義為過渡單元。不妨記活躍單元、非活躍單元以及過渡單元的集合分別為PosElemSet、NegElemSet和NeuElemSet，將

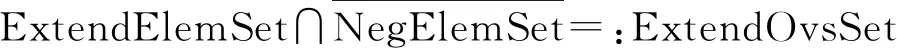
(7)

定義為延拓型重疊單元的集合。易知

VolElemSet=PosElemSet∪NegElemSet∪

NeuElemSet∪ExtendOvsSet

(8)

其中：等號右側4個元素之間互不相交。

式(7)表明，經過壁面距離準則篩查后，如果延拓型單元不屬于非活躍單元集合，那么它將被識別為重疊單元。

3) 任取體單元neg∈NegElemSet，如果存在體單元neu∈NeuElemSet，使

NodeList(neg)∩NodeList(neu)≠?

(9)

那么將neg歸入一般性重疊單元集合GeneralOvsSet，否則將其歸入洞內單元集合HoleElemSet。NodeList(neg)和NodeList(neu)分別表示體單元neg和neu的節點元素集合。此處單元分類的幾何意義是：在洞邊界附近，與過渡單元相鄰的非活躍單元轉化為重疊單元；與過渡單元不相鄰的非活躍單元轉化為洞內單元。

4) 場單元集合的定義為

FieldElemSet:=PosElemSet∪NeuElemSet

(10)

需要說明的是，過渡單元是同時具有活躍節點和非活躍節點的體單元，因為它恰好跨越重疊挖洞邊界，所以將與另一網格組上的過渡單元交織在一起；為避免不同網格組上的重疊單元互為對方的貢獻單元，在式(10)中，過渡單元最終轉化為場單元。重疊單元集合定義為

OvsElemSet:=GeneralOvsSet∪ExtendOvsSet

(11)

至此，結合第3)步的洞內單元HoleElemSet，最終完成了單元分類

VolElemSet=FieldElemSet∪HoleElemSet∪

OvsElemSet

(12)

從本文重疊網格裝配算法的構造過程可以看出，與圖示法相比，基于集合論語言的描述方式具有如下4個方面的優勢：

1) 具有普適性，不受網格幾何形狀復雜程度或面、體單元類型多樣性的影響。

2) 能夠清晰表述多組網格重疊時的復雜映射關系。

3) 能夠精確判斷延拓型外緣邊界與距離挖洞邊界相交等復雜情形。

4) 可作為算法分析的有力工具，輔助提升并行裝配效率。

2 自動化并行重疊網格隱式裝配方法

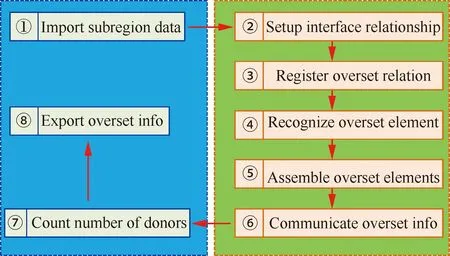
圖1顯示重疊網格的并行裝配流程，包含幾何信息輸入、網格組自動配對、重疊單元隱式裝配、插值信息輸出等4個步驟。

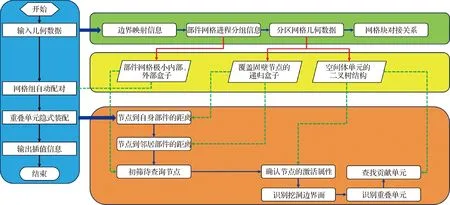
圖1 重疊網格并行化裝配流程

步驟1左側(藍色)部分是算法主線，依次為分區網格幾何信息的輸入、部件網格組之間重疊關系的自動識別、重疊單元的隱式裝配以及插值信息的輸出。

步驟2右上(綠色)部分是幾何數據的基本構成，包含邊界映射信息、部件網格進程分組信息、分區網格幾何數據以及網格塊對接信息。其中，邊界映射信息主要用來識別固體邊界面以及部件網格的外延拓邊界面；在挖洞過程完成后，網格塊對接關系用來跨進程識別重疊單元。

步驟3右中(黃色)部分是重疊裝配所需的主要數據結構，它們根據原始幾何信息構建。其中，部件網格極小內部盒子、外部盒子用來輔助網格組自動配對；覆蓋固壁節點的遞歸盒子用來對查詢節點進行初步篩查；空間體單元的二叉樹結構用于單元節點或格心貢獻單元的快速查詢。

步驟4右下(橙色)部分顯示具體的重疊單元隱式裝配過程，包括并行計算節點到自身部件和鄰居部件距離、初篩待查詢節點、確認節點激活屬性、識別挖洞邊界、識別重疊單元以及查找貢獻單元等7個步驟，(綠色)虛線條展示了各步驟所需的數據結構。

2.1 重疊網格組并行分區策略

重疊網格并行裝配算法是與網格組分區策略緊密結合在一起的。假設存在N個進程參與流場計算，那么上述M個網格組存在兩種分區策略。

策略T1把全體網格組包含的網格塊視為一個整體，根據體單元數負載均衡原則，使用Greedy算法或METIS算法進行統一分配，如圖2(a)所示。

策略T2結合網格組體單元數在整體網格中所占的比重，計算其所需的進程數，然后將當前網格組均勻分配到相應的進程組中，如圖2(b)所示。

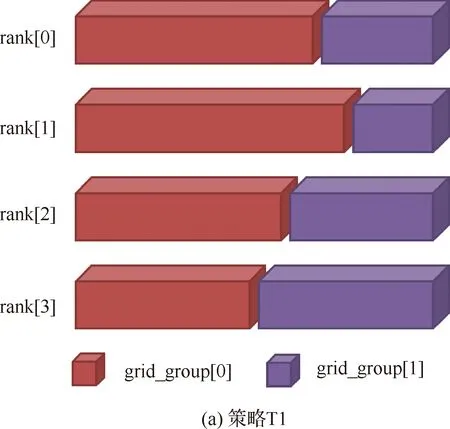
圖2 兩種剖分策略對比

文獻[21]中的重疊網格裝配方法使用T1策略能夠保證體單元分配結果的高度均衡性，但也容易使每個網格組上形成過多的碎片化網格塊，從而影響并行計算效率。在重疊網格并行化裝配算法中，兩個網格組涉及的進程組間需要頻繁進行數據通信；此時使用較少的進程數容納當前網格組的各個網格塊，能夠有效提高算法的并行效率。因此，采用T2策略進行網格分區。

2.2 網格組自動配對技術

在傳統的重疊網格裝配算法中，需要在圖形界面下人工指定網格組間的重疊關系，比如使用邏輯矩陣來描述。對于多體相對運動的情形，各網格組之間的相對位置與重疊關系通常是動態變化的，這些特點決定了人工配對操作難以滿足重疊網格自動化裝配的需求。常興華等[22]為提升大規模重疊網格的裝配效率與自動化水平，使用包含每個網格塊的長方體輔助判斷重疊關系，其中長方體表面分別與坐標軸垂直。這種方法本質上是使用大量的簡單長方體實現網格組區域的幾何逼近，將網格組重疊關系判斷問題轉化為相應長方體集合的求交邏輯運算；但是，這種方法導致過于碎片化的分區結果，根據Navier-Stokes (N-S) 方程的數值迭代理論，它將使收斂歷程大大延長，從而降低流場求解的效率。受文獻[15]中方向適應型邊界盒子的啟發，本文建立了關于部件表面網格點坐標的協方差矩陣，結合譜分析技術，構造了部件網格組的極小內部盒子與極小外部盒子，以此輔助網格組區域重疊關系的快速識別。

在第i個部件compi∈CompSet上，設固壁節點集合SolidNodeSeti的元素個數為ms，那么可以把所有節點的坐標依次存儲于3個ms維向量中：

(13)

式中：(xms,yms,zms)為編號s的固壁節點空間坐標。協方差矩陣為

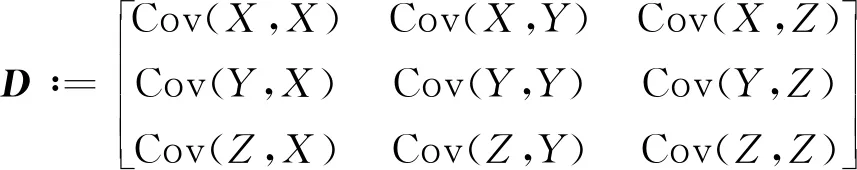
(14)

根據協方差運算的可交換性可知：D為對稱矩陣，其特征系統中3個特征向量兩兩正交。通過Householder變換可將其約化成三對角陣，進一步使用QR方法即可得到D的全部特征值及其特征向量。設特征向量的規范化結果為

ns=[As,Bs,Cs]Ts=0,1,2

(15)

給定方向序號s，以ns為基準法向量建立空間平面參數方程：

Asx+Bsy+Csz+λs=0

(16)

依次遍歷SolidNodeSeti中的元素并取參數λs的上下確界，即得方向部件的2個臨界方程。3個特征方向的臨界方程使部件表面網格包含在一個極小長方體內，稱其為極小內部盒子MIBi，如圖3紅色線條所示。

如果保持特征方向不變，將上述運算中的集合SolidNodeSeti替換成整體網格組節點集合NodeSeti，那么整體網格組將包含在新的極小長方體內，稱其為極小外部盒子MEBi，如圖3藍色線條所示。對網格生成有如下附加要求：極小內部盒子覆蓋的空間區域包含在整個網格組區域中，這在網格生成過程中是容易實現的；同時，網格組外緣表面適當遠離邊界層網格也是提升重疊插值精度的要求。圖3展示的是螺旋槳單葉片網格上極小內部盒子與極小外部盒子的包含關系，而圖4展示了整個螺旋槳各部件網格相互重疊關系。

圖3 螺旋槳單葉片極小內部/外部盒子

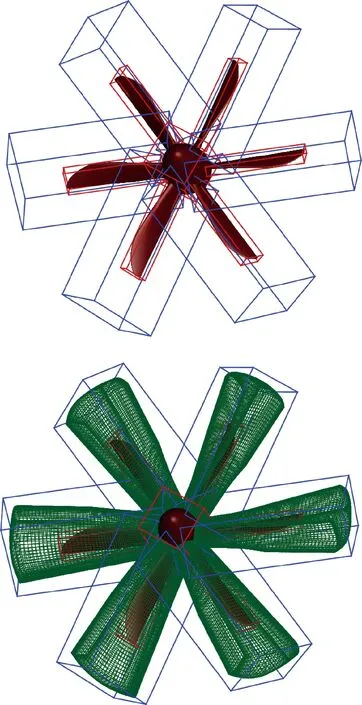
圖4 螺旋槳葉片各部件網格重疊關系

任意給定網格組gpi，設其覆蓋區域為Di，那么存在集合關系式

MIBi?Di?MEBi

(17)

對于當前網格組gpi(稱為源網格組SG)，如果對另一組網格gpj，關系式：

MEBi∩MEBj=?

(18)

成立，那么

Di∩Dj=?

(19)

即當前狀態下gpi與gpj不存在相互重疊關系；否則，稱gpj為與gpi存在可能重疊關系的目標網格組TG。式(18)的邏輯判斷可以根據圖5所示的分離平面法快速完成：依次遍歷源網格組SG和目標網格組TG的3個特征方向，那么該式成立的充要條件為：存在以特征方向為法向量的空間平面SP，使MEBi與MEBj分居其兩側。圖6描述了源網格組與目標網格組(為目標網格組的全局編號)之間的重疊關系，其中，與當前源網格組SG發生重疊關系的目標網格組TG的總數為L；在并行計算環境下，源網格組的各個子塊grid_s分布在編號連續的NG個進程中，而它的某個目標網格組(以TG[2]為例)的各個子塊grid_t分布在編號連續的MG個進程中。

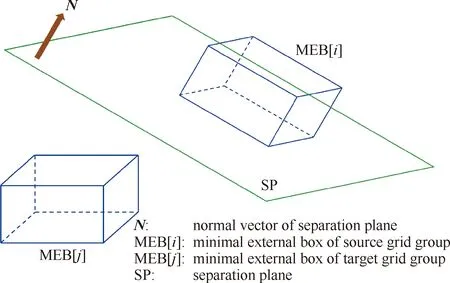
圖5 空間分離平面法

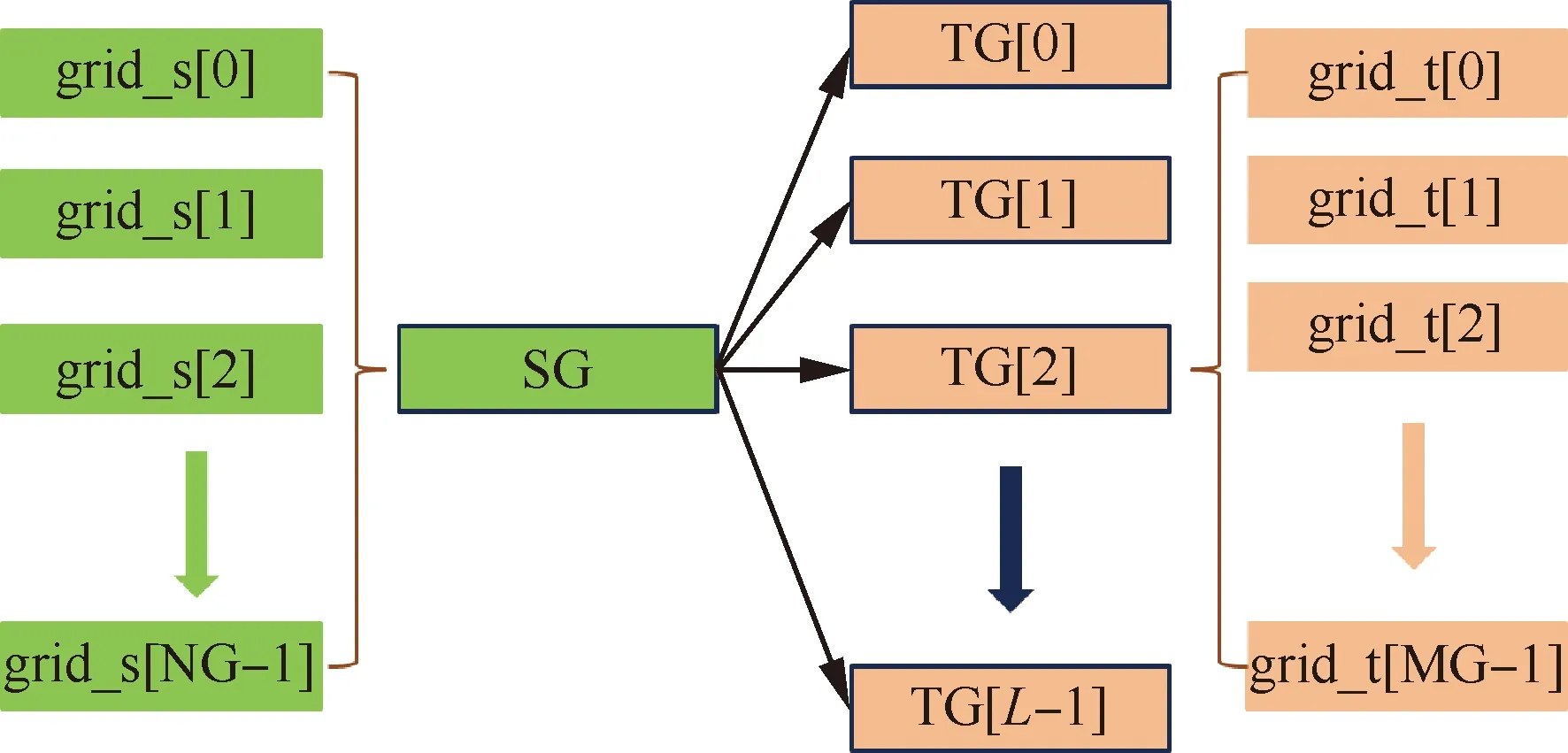
圖6 源網格組與目標網格組的重疊關系

使用圖6所示的映射關系，可以對多組網格間的復雜重疊關系進行分解。從整體上來說，優先遍歷當前的源網格組SG；對于特定SG，局部遍歷與之重疊的多個目標網格組TG。

2.3 自動挖洞的并行化實現

在第1節中，描述重疊網格自動挖洞的壁面距離準則包含兩個方面內容：一是網格節點壁面距離的計算；二是網格節點與體單元之間的覆蓋關系。在當前網格組gpi上，如果直接遍歷集合NodeSeti并對每個網格點元素P∈NodeSeti同時執行上述分析，那么不僅會使程序編寫難度急劇提高，而且會使源網格組與目標網格組之間的通訊壓力迅速增長，進而限制該算法在大規模并行計算中的應用。反之，如果首先對NodeSeti中所有元素基于距離參數比較法計算距離參數，就可以大大降低判斷節點與體單元覆蓋關系時的計算量與通訊壓力，其原理描述如下。

對于?gpi所對應的目標網格組gpj(j=j0,j1,…,jL-1)，如果?P∈NodeSeti，條件C1：

d(P,SolidNodeSetj)>d(P,SolidNodeSeti)

(20)

成立，那么P∈PosNodeSeti。作為式(3)的互斥條件之一，式(20)使用單純的距離判據排除了大量待查詢的節點。

此外，結合2.2節關于極小外部盒子的定義可知，如果?P∈NodeSeti，條件C2：

(21)

成立，那么可以推出

(22)

作為式(3)的另一個互斥條件，式(22)根據網格組的極小外部盒子的空間相對位置進行間接篩查，同樣可知P∈PosNodeSeti。C1與C2稱為距離初篩條件與覆蓋初篩條件，據此可提升重疊網格并行化挖洞算法的效率。

圖7描述了當前源網格組SG壁面幾何信息的收集以及與各目標網格組TG共享的過程：非阻塞通訊模式下，在SG包含的各個進程組內，對相應網格塊grid_si(i=0,1,…,NG-1，NG為分區后SG包含的網格塊總數)上的壁面節點坐標序列進行數據壓碼操作，形成NG個二進制數據流solid_s，在主進程中通過數據容器solid_node_collector加以匯總后，分別在SG與TGj(j=0,1,…,L-1，L為SG對應的目標網格組個數)所在的進程組內共享并解碼，形成完整的SolidNodeSet信息后，對節點壁面距離信息進行更新。

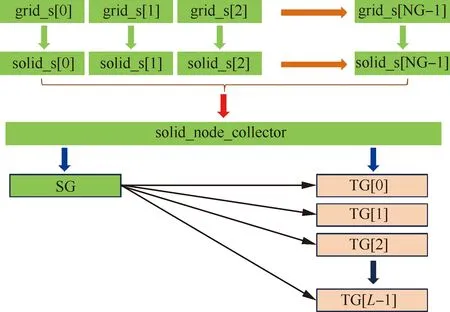
圖7 源網格組壁面幾何信息收集與共享

圖8描述了節點壁面距離參數的定義：對源網格組SG(gpi)上任意給定網格節點P∈NodeSeti，令ds(P)∶=d(P,SolidNodeSeti)為P到SG壁面的距離，dtj∶=d(P,SolidNodeSetj)為P到TGj壁面的距離，其中j取0～L-1范圍內的整數；令dt(P)∶=MinVal{dt[0],dt[1],…,dt[L-1]}，那么，ds與dt就構成了距離比較判據的兩個重要參數。在并行計算框架下，若直接對ds與dt進行計算，則存在兩種方式：① 把P的信息發送L次，分別與SolidNodeSetj計算出dtj，然后通過全局規約操作得到dt值；② 把SolidNodeSetj的信息發送到P所在的進程，對其依次遍歷，按最小值準則不斷更新dt值。可見，方式①的通訊壓力較大，全局規約操作將影響計算效率的提升，因此采用后一種方式計算ds與dt。

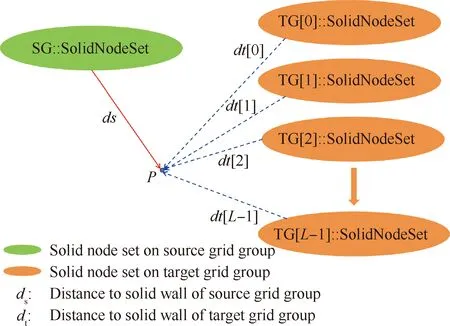
圖8 節點壁面距離參數定義

空間節點的壁面距離是重疊網格隱式裝配方法的關鍵參數之一，如果采用線性查找方法，遍歷所有的壁面點后取最小值，那么，當壁面節點總數很大時，計算成本將急劇升高；同時，這種簡單查找法也難以適應網格運動、網格自適應時壁面距離頻繁更新的情形。相比之下，基于點集樹形排序思想的方盒切割算法[23]能夠很好地處理這一問題，它包括固壁點集臨界長方體(方盒)序列的生成和最近距離點的查找兩部分內容，其中，針對臨界長方體序列的輔助分析，可以在點集遍歷過程中動態排除無關的子集，從而大幅提升壁面距離的計算效率。

臨界長方體序列的構造分為如下4個步驟：

步驟1取網格組gpi共享的壁面節點集合SolidNodeSet[i]，沿著平行于坐標平面的方向，根據式(23)分析壁面節點坐標分量的上下界，構成臨界長方體序列根結點的6個基本參數，它們分別是

(23)

步驟2在節點集坐標分量最大的變化區間上進行排序與二分法操作，構造當前節點集的左右子集以及相應的臨界長方體參數。分別計算

(24)

不妨假設

δz<δy<δx

(25)

然后，對壁面節點序列按照x坐標大小排序，并采用二分法生成SolidNodeSeti的2個子集SubNodeSeti0與SubNodeSeti1。

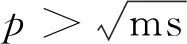
步驟4當臨界長方體構造完成后，僅收集所有的葉子結點(不可分的臨界長方體)，形成壁面距離計算的基礎查詢數據集。經過若干層級的分解，原始的SolidNodeSeti可以寫成一系列節點子集的并集，即

SolidNodeSeti=SubNodeSeti0∪SubNodeSeti1∪

…∪SubNodeSeti(NSub-1)

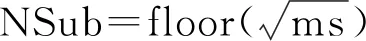
此時，對于每個SubNodeSetis，分別以空間平面

(26)

構成臨界長方體Capsules，以此覆蓋集合SubNodeSetis，如圖9和圖10所示。

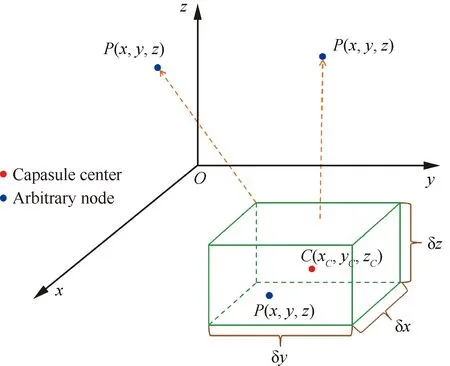
圖9 定點和臨界長方體的距離

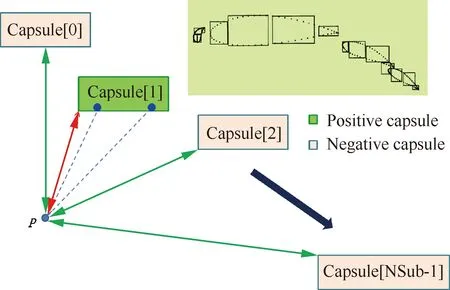
圖10 壁面距離計算的臨界長方體算法

任意給定空間網格節點P，可以按照如下4個步驟在集合SolidNodeSeti中快速查找出最近的固壁節點：

步驟1依次計算當前網格節點到基礎查詢數據集中每個臨界長方體的距離，其定義需要滿足這樣的條件：無論網格點在臨界長方體內部還是外部，它與臨界長方體的距離將小于到其中任意固壁節點的距離。記P到每個Capsules區域的距離為d(P,Capsules)。根據圖9，設P的坐標為(x,y,z)、Capsules的格心坐標為(xC,yC,zC)，那么，對于任意相對位置，d(P,Capsules)具有統一形式：

d(P,Capsules)=

(27)

式中：

f(ξ,η,ζ):=

(28)

為每個Capsules對象設置邏輯變量Logic表征其激活屬性，初始值為TRUE；同時，初始化

d(P,SolidNodeSeti)=LARGE_DISTANCE

(29)

式中：LARGE_DISTANCE=1.0×1040。

步驟2在當前所有激活的臨界長方體中進行遍歷，選取使d(P,Capsules)達到最小值的Capsules。如果符合條件的Capsules存在，那么記錄其編號s以及d(P,Capsules)，此時最近的固壁點位于其中的可能性很大，為進一步確認，通過步驟3對臨界長方體內的固壁點集進行更加詳細的判斷；否則，在激活狀態的臨界長方體不存在時，轉向步驟4即可。

步驟3一邊計算網格節點與固壁節點的距離，一邊將其與處于激活狀態的各個臨界長方體的距離進行比較，如果后者大于當前的距離，那么其中的任意固壁節點皆不可能成為最近距離點，所以不再予以考慮，具體過程描述為：在Capsules覆蓋的子集SubNodeSetis上，計算

d(P,SubNodeSetis)∶=

MinVal(d(P,Q)|Q∈SubNodeSetis)

(30)

令Capsules的邏輯變量Logic=FALSE且更新d(P,SubNodeSetis)，即

d(P,SolidNodeSeti)=

min(d(P,SolidNodeSeti),d(P,SubNodeSetis))

(31)

遍歷全部臨界長方體，如果臨界長方體Capsules滿足條件

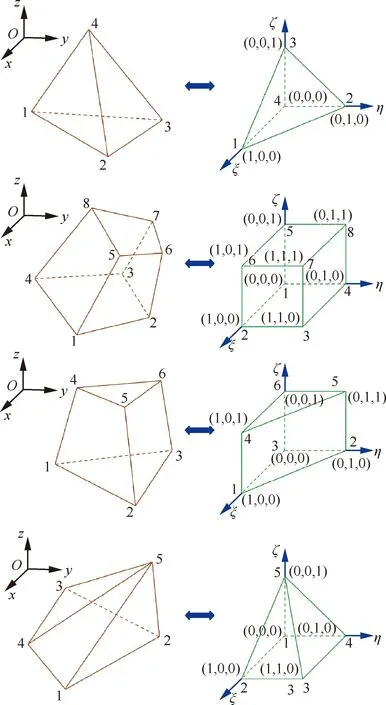
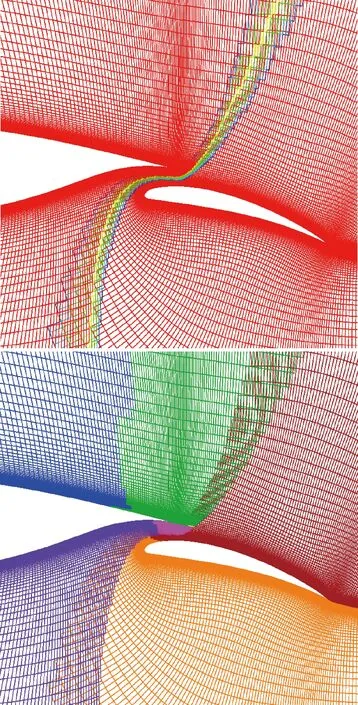
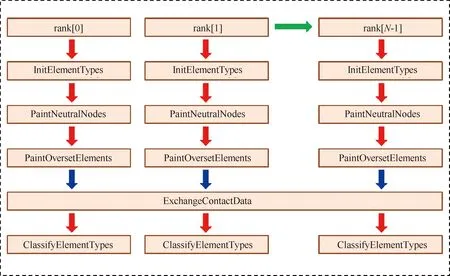
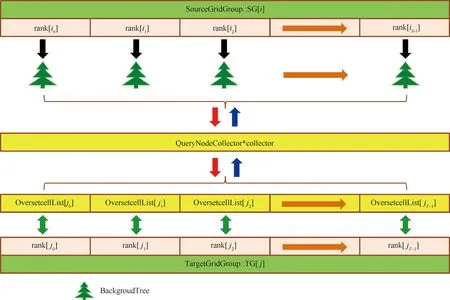
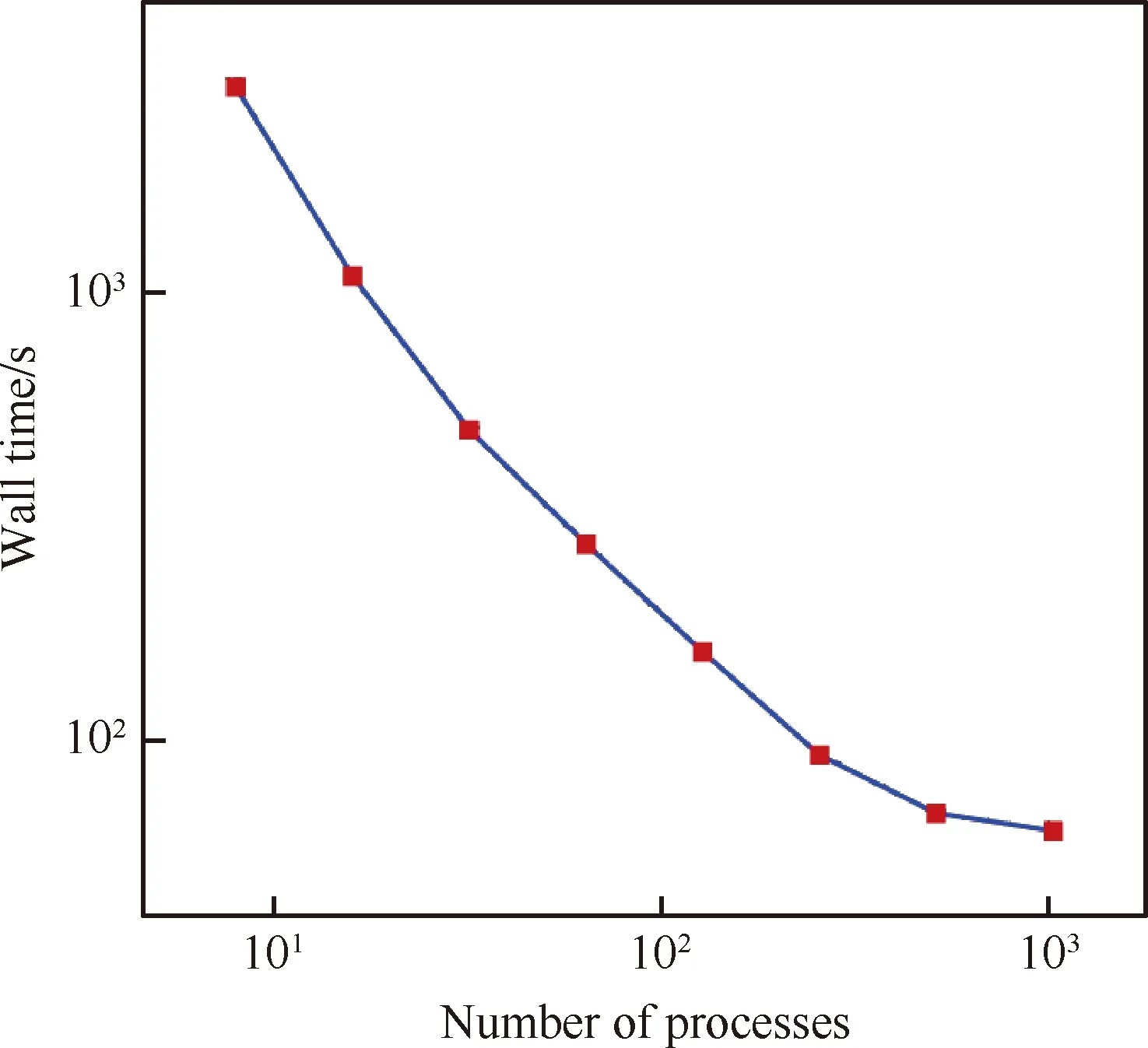
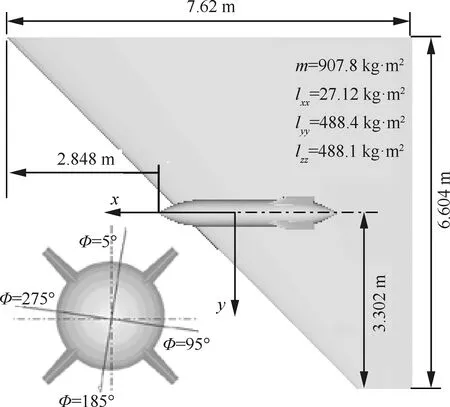
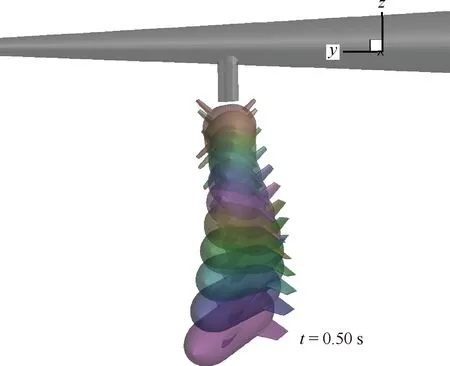
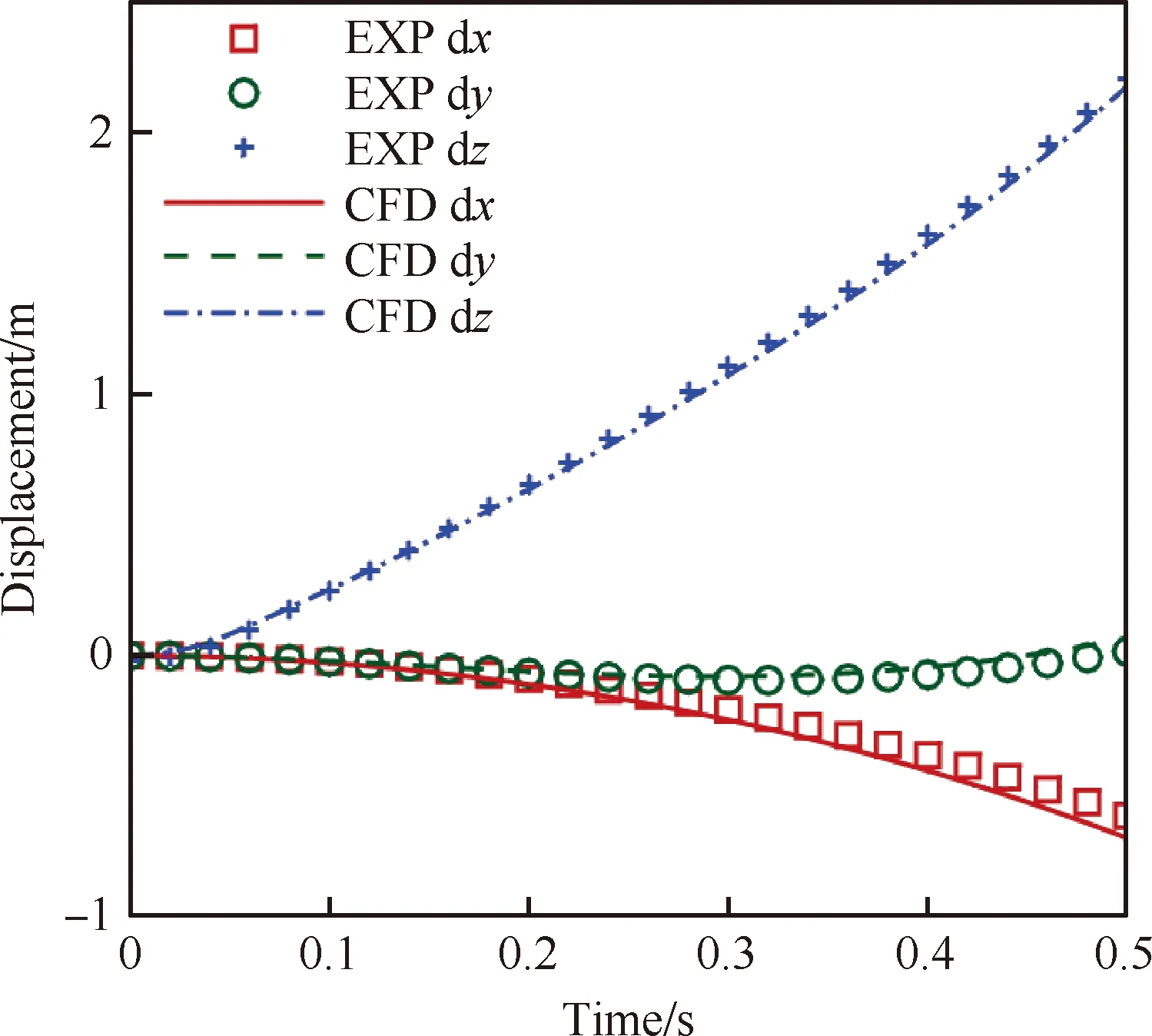
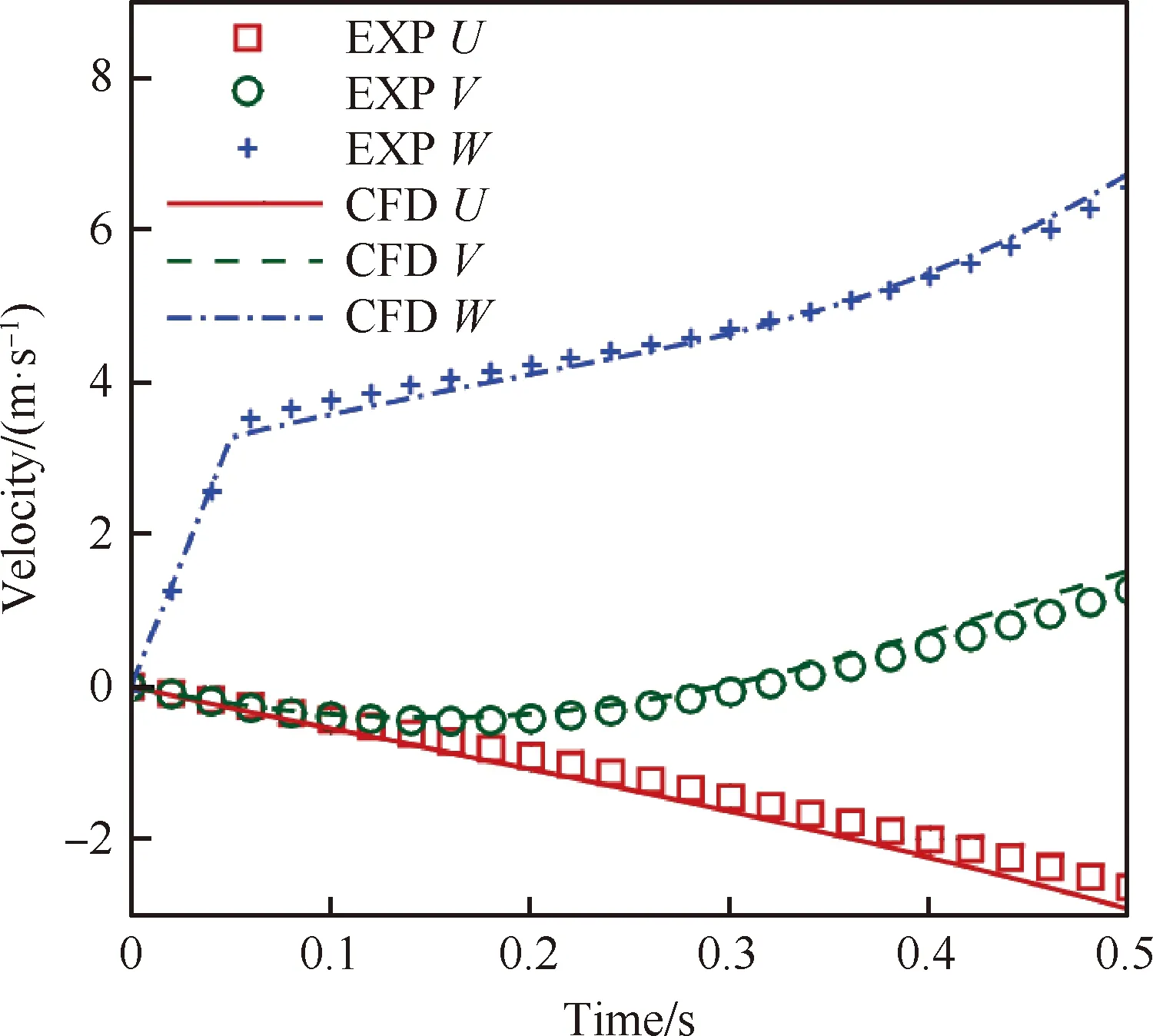
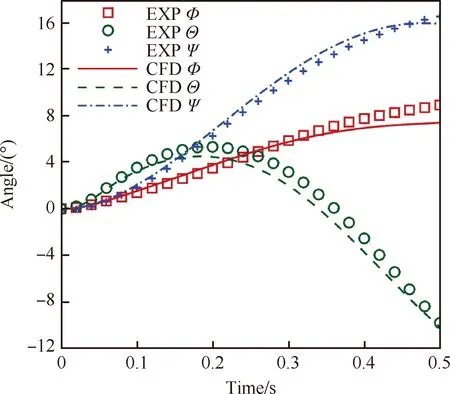
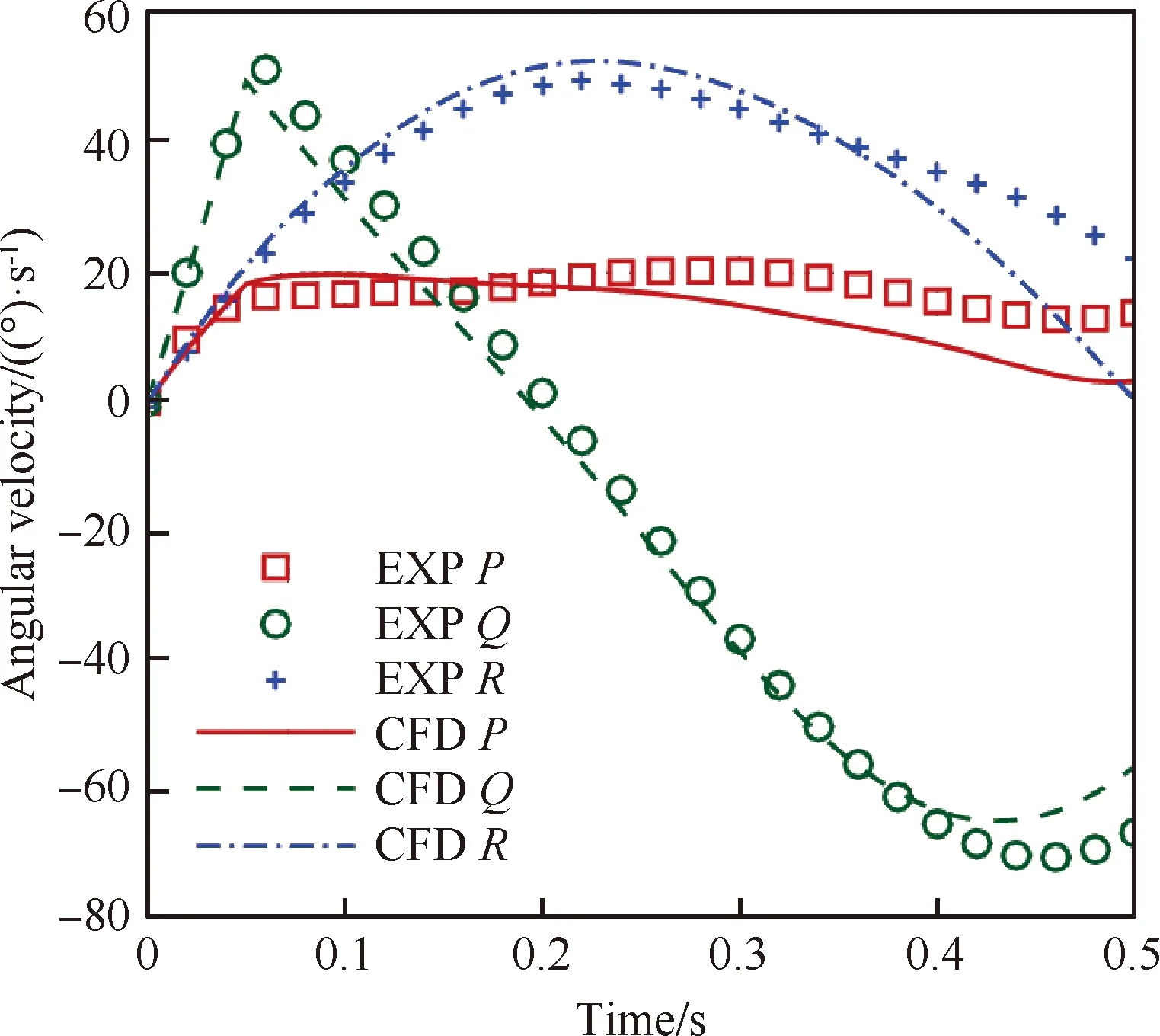
d(P,SolidNodeSeti)

(32)

那么，為其邏輯變量賦值Logic=FALSE；最后，返回步驟2。

步驟4當步驟2和3的循環判斷結束后，即可得到最終的壁面距離d(P,SolidNodeSeti)。

在網格組gpi上，結合距離初篩條件與覆蓋初篩條件，定義查詢節點的集合

QueryNodeSeti:={P|dt(P)

Dj0∪Dj1∪…∪DjL-1}

(33)

且QueryNodeSeti滿足

NegNodeSeti?QueryNodeSeti?NodeSeti

(34)

式中：源網格組gpi與目標網格組gpjs極小外部盒子參數可以在并行編程框架下實現共享，js∈{j0,j1,…,jT-1}為目標網格組的編號。

對于集合關系式(34)，根據覆蓋關系式(17)從QueryNodeSeti篩選出NegNodeSeti，在并行編程框架下的查詢算法以及數據流如圖11所示。

圖11 節點查詢算法及插值信息數據流

設當前源網格組SG各子網格塊分布在編號連續的S個進程中，在每個進程上，子網格塊將按照六維超子空間分割法[24]生成獨立的二叉樹結構，為任意外部節點提供快速查詢服務；同時，按照式(5)，根據延拓型物理邊界，SG在每個進程內子網格塊體單元被初步劃分為一般單元與延拓單元。設SG的任意目標網格組為TG，因為查詢節點分布在編號連續的T個進程中，每個進程對應查詢節點的子集QueryNodeListjs。在非阻塞通訊模式下，主進程對QueryNodeListjs進行收集，即

QueryNodeSetj=QueryNodeListj0∪

QueryNodeListj1∪…∪QueryNodeListjT-1

(35)

然后將其共享到SG所在的進程組內進行查詢操作，其步驟如下：

步驟1貢獻單元的并行查找與插值信息的計算。在上述共享機制作用下，SG涉及的每個進程內皆包含目標網格組TG上查詢節點集合QueryNodeSetj的完整信息。任意給定查詢節點對象P∈QueryNodeSetj，通過局部二叉樹查詢算法，如果存在體單元velem∈GenElemSeti覆蓋P，那么在對象P中記錄如下3種信息：① velem所在的當前進程編號以及局部體單元序號；②P在velem中的相對坐標；③P到SG壁面的距離d(P,SolidNodeSeti)。由于已計算出velem各個節點到自身網格組的壁面距離參數ds，因此結合②中的相對坐標以及距離函數的空間連續性，即對d(P,SolidNodeSeti)進行三線性插值。如果當前進程內不存在體單元velem∈GenElemSeti覆蓋P，那么擦除對象P在當前進程的全部信息。

步驟2貢獻單元存在時節點的篩查。在SG涉及的每個進程內，剩余查詢節點信息通過圖11中的信息收集器collector匯總后，在TG包含的進程組內進行信息共享。在TG各子網格塊所在的進程內，皆包含collector共享的有效查詢結果。如果查詢節點P原始的進程編號與當前進程一致，那么結合其局部節點編號，在當前進程網格塊的相應位置更新信息：如果dt(P)

步驟4剩余查詢節點的處理。在式(34)中，查詢節點集包含了非激活點集，在確認階段，排除所有的非激活點集后，剩余的查詢節點P都需歸入一般節點集合，即P∈GenNodeSetj。

主要對4種非結構體單元進行處理，即四面體、六面體、三棱柱和金字塔。為確定給定節點與體單元的相對位置，需要把物理坐標系下的體單元映射成為計算坐標系下的標準計算單元。圖12展示了4種類型單元與標準單元之間的微分同胚關系，其中物理坐標系下體單元的覆蓋區域可用形函數的線性組合加以描述：

圖12 4種類型單元與標準單元之間的微分同胚關系

(36)

式中：(x,y,z)為體單元內部任意一點的物理坐標；(ξ,η,ζ)為對應的計算坐標；M為單元角點總數；(xs,ys,zs)為角點物理坐標。不同類型velem單元的形函數序列如表1所示。

表1 4種類型單元的插值形函數序列

為了確定給定節點P(x*,y*,z*)在標準計算單元中的相對坐標(ξ,η,ζ)，建立非線性方程組

(37)

構造Newton迭代序列

(38)

式中：下標n與n+1用來區分當前時間層與更新時間層的變量。設收斂結果(ξ,η,ζ)滿足條件：

那么，可以得到P∈velem的結論。

至此，已實現網格節點分類算法的并行化工作。在上述“初篩+確認”模式中，基于兩種距離參數以及網格組極小外部盒子參數對可疑節點的篩查，使各進程內查詢節點集合的規模得到了有效的控制；同時，對于目標網格組TG來說，伴隨著洞內節點的不斷剔除，它在與另一組網格組SG進行配對時，查詢節點的總量將進一步的縮小。這些措施都極大降低了并行通訊的壓力。

2.4 重疊單元的識別及并行化裝配

根據第1節的介紹，在完成網格節點分類的基礎上，可以結合單元與節點的拓撲關系，完成場單元、洞內單元以及重疊單元的劃分。在2.3節描述的單元分類過程中，第1)2)4)步可以在各自進程內通過“節點-單元染色”方式獨立進行。然而，在第3)步中，與過渡單元相鄰的非活躍單元被定義為一般性重疊單元；如果過渡單元與非活躍單元的分界面與網格分區邊界面存在重合(如圖13所示)，那么需要通過分區邊界處點對點的并行通訊完成單元類型信息的傳遞，其算法流程如圖14所示。

圖13 過渡單元與非活躍單元分界面與網格分區邊界面重合情況

在圖14所示的各個進程內，沿著箭頭指向，重疊單元識別算法的并行化共分為5個步驟：① 根據網格節點的激活屬性將體單元劃分為活躍體單元、非活躍體單元、過渡體單元與延拓型重疊單元4種類型；② 對過渡體單元包含的網格節點(稱為過渡節點)進行染色標記；③ 在當前進程內，根據已染色的過渡節點識別一般類型重疊單元與洞內單元；④ 根據網格分區邊界處的并行通訊，識別一般型重疊單元；⑤把一般型重疊單元與延拓型重疊單元統一歸并到重疊單元集合中，活躍體單元與過渡體單元統一歸并到場單元集合中。

圖14 重疊單元的并行識別過程

圖15展示了使用二叉樹技術建立重疊單元格心與貢獻體單元之間“插值-覆蓋”映射的過程。圖15與圖11有較高的相似度，特別是在網格節點分類(即并行化自動挖洞)時使用的二叉樹結構未發生變化。此處主要有2點不同：① 目標網格組上收集的節點信息變更為重疊單元格心信息；② 在源網格組上，二叉樹查詢算法對應的有效貢獻單元附加約束屬性由一般型單元變更為場單元。有效貢獻單元的約束條件，有效避免了不同網格組重疊單元互相插值的異常現象，從而使流場迭代過程順利進行。

圖15 重疊單元的并行裝配

3 算例驗證

本文采用面向對象編程思想，使用C++語言和MPI并行編程模型實現了重疊網格隱式裝配算法的并行化，從而建立了圖16所示的“重疊網格縫紉機”(Overlapping Grid Sewing Machine, OGSM)工具庫。

圖16 OGSM運行流程

OGSM描述的流程共分為8個節點，它們分別是：① 讀入當前進程子區域的網格拓撲信息；② 建立網格分區邊界的并行通訊架構；③ 自動化注冊網格組重疊關系；④ 基于壁面距離準則識別重疊單元；⑤ 在背景網格上查找重疊單元的最優貢獻單元；⑥ 重疊裝配信息的跨進程整理；⑦ 統 計當前進程內子區域上貢獻單元的總數；⑧ 輸 出重疊插值以及單元分類信息。其中，左側(藍色)方框表示的是OGSM的外部接口，右側(綠色)方框內是重疊網格并行裝配算法的內部實現。

3.1 五球體部件

為了獨立測試OGSM的并行裝配能力，對包含5個球體部件的重疊網格進行裝配。如圖17所示，每個球體部件獨立生成非結構網格，體單元總量為1.2億。在z=0平面內進行切割，可以看到5個區域之間的自動裝配結果。其中，藍色曲線為網格分區邊界，綠色部分為重疊單元。在該算例中，部件網格的外延拓邊界與挖洞邊界相交，球體之間的挖洞邊界遵循了壁面距離準則，本文的自動挖洞邏輯的準確性得到了檢驗。圖18展示了算法的并行效率曲線，隨著分區進程數的增加，裝配時間單調下降。

圖17 重疊單元和場單元切片(截面方程：z=0)

圖18 不同進程對應的墻上時間

3.2 WPFS模型

為了進一步檢驗OGSM重疊單元與貢獻單元插值關系的準確性，本文通過接口模式將其嵌入至流場求解器PMB3D[25]中，對WPFS(Wing-Pylon-Finned Store)投放算例的非定常流場進行了數值模擬。

WPFS模型[26]是美國發起的用于CFD驗證的機翼外掛物分離投放簡化模型，其中單外掛物分離投放試驗由AEDC于1990年完成，該模型作為標準算例通常用于對外掛物分離數值方法進行考核。如圖19所示，研究模型的機翼為45°后掠的三角翼，采用NACA64A010翼型，無扭轉。外掛物的頭部為尖拱形，中間為圓柱，共有4片尾翼，呈X形分布。尾翼采用NACA0008翼型。外掛物質心位置距頭部頂點1.417 3 m，參考長度0.508 m，參考面積0.202 69 m2。實驗模擬研究兩個狀態下的投放分離，狀態1的環境高度為7 925 m(26 000 ft)，來流馬赫數0.95；狀態2的環境高度為11 582 m(38 000 ft)，來流馬赫數1.2，機翼無攻角和側滑角。為了確保外掛物安全分離，在投放初始瞬間，加入了兩點彈射力的作用，彈射力1的作用點距頭部尖點1.24 m，大小10 679.4 N，彈射力2距頭部尖點1.75 m，大小42 717.5 N。在外掛物離開載機0.1 m(分離時間0.055 s)以后，彈射力消失。圖19中給出了外掛物的質量以及3個方向上的轉動慣量，由于外掛物關于軸和軸對稱，它的慣性積Ixy=Iyz=Izx=0 kg·m2。

圖19 外掛分離試驗模型參數

WPFS算例中，在機翼和彈體部件周圍生成多塊結構網格，前者對應的節點總數和體單元總數分別為5 124 792和4 798 080，后者對應的節點總數和體單元總數分別為1 722 242和1 585 664。整個計算區域劃分到64個進程中。在每個進程上，合并重合的節點單元和面單元，多塊結構網格即轉化為獨立的非結構網格(原有各個網格塊可以是不連通的)。使用OGSM進行重疊裝配后，依舊采用多塊結構網格求解器進行RANS方程的非定常數值模擬，其中對流項和黏性項分別使用Roe格式和SA湍流模式進行離散，時間方向上采用雙時間步推進，結合minmod限制器抑制非物理解的生成。

在雙時間步推進過程中，流場求解器PMB3D的每個物理迭代步劃分為300個子迭代步，單個子迭代步消耗的時間為1.49 s；因為彈體相對于機翼處于不同位置時，依據壁面距離準則得到的挖洞邊界形態各不相同，從而導致重疊裝配時間發生一定的變化，所以本文僅選取初始時刻對OGSM模塊的裝配時間進行統計，對應的裝配時間為9.29 s，占每個物理迭代步消耗時間的比率為2.1%，能夠滿足當前算例的數值模擬需求；同時，壁面距離的計算時間為3.12 s，可疑查詢節點的并行確認時間為4.63 s，它們與總裝配時間的比率分別為33.5%和49.9%；相比之下，生成背景網格二叉樹的時間為0.22 s，重疊單元插值系數的并行計算時間為0.69 s，它們與總裝配時間的比率僅為2.3%和7.4%。結合本文的算法流程可以判斷，隨著進程數的增加，切割盒子序列的結構未發生明顯變化，為適應壁面節點規模不斷增加的情形，今后需對壁面距離的高效并行算法做更加深入的研究；同時，基于部件網格的幾何特征，挖掘新的初篩判據，在早期排除更多的待查詢節點，也有助于進一步降低并行通訊壓力，從而提升OGSM的裝配效率。

圖20給出的是狀態1(Ma=0.95)外掛物表面壓力系數Cp和空間流線，可以看到初始時刻外掛物受到來流外洗的作用，產生向右的偏航力矩。在該算例中，機翼為前緣后掠角45°的三角翼，從翼根開始，氣流在受到機翼的阻滯作用后，產生沿橫向流動的速度分量。低于外掛物來說，頭部靠機翼內側的地方迎著橫向流動，壓力系數較另一側高，因此產生頭部向機翼外側方向偏轉的偏航力矩。

圖20 外掛物表面壓力系數和空間流線分布

圖21顯示的是外掛物處于掛載狀態時展向截面馬赫數云圖，機翼上下表面大部分區域都是超聲速流動，靠近機翼后緣的地方，上下表面均形成了激波，波后流動速度為亞聲速。圖21同時給出了截面上的網格分布，從中能夠清晰地看到重疊邊界的位置，在跨過重疊邊界的地方，壓力系數云圖分布連續，反映了在這些地方流場信息得到了正確的傳遞。

圖21 外掛物處于掛載狀態時展向截面馬赫數云圖

圖22給出的是外掛物分離軌跡示意圖，其中模擬時長t為0.5 s。從圖中可以看到，外掛物在分離過程中，產生了頭部向機翼外側的偏航運動；在俯仰方向上，分離初始階段產生的是抬頭運動，隨后在尾翼的穩定作用下產生低頭運動。圖22反映了外掛物分離過程的總體運動趨勢，定性地描述了運動過程，下面將給出定量描述。

圖22 外掛物分離軌跡

圖23和圖24分別給出的是外掛物質心位置(dx、dy、dz)和線速度(U、V、W)變化曲線，可以看到在重力和彈射力作用下，外掛物向機翼下方移動，其運動幅度在3個方向上是最大的；同時在阻力作用下，外掛物向機翼的后方移動；在橫向方向上(y方向)，外掛物先是向機翼的內側移動，然后在t=0.35 s以后，外掛物開始向機翼外側移動，盡管移動幅度較小，計算仍比較準確地模擬這種變化趨勢。總的來說，在所顯示的時間范圍內(t=0.5 s)，計算得到的質心線速度和位移和實驗值都比較吻合，稍顯不足的是由于黏性計算的阻力大于試驗值，所以模擬得到的后向移動速度略大。

圖23 外掛物質心位置變化曲線

圖24 外掛物線速度變化曲線

圖25和圖26分別給出的是外掛物的姿態角和角速度的時間歷程，其中P、Q、R分別為體軸系的3個角速度分量，Φ、Θ、Ψ分別為滾轉角、俯仰角和偏航角，用來表示從地軸系到體軸系的變換。對于俯仰運動來說，在分離初始階段，彈射力產生較大的抬頭力矩，彈射力維持的時間到t=0.055 s， 之后彈射力作用消失，作用在外掛物上的氣動力和力矩開始起主導作用，這時候氣動力產生的是低頭力矩，在t=0.2 s以后，外掛物開始下俯運動，本文計算的最大俯仰角度和下俯開始位置都和試驗值吻合良好。在偏航方向，從分離開始外掛物偏向機翼的外側，在t=0.5 s偏航角約為16°，在t≤0.4 s計算的偏航角與試驗值吻合良好，t>0.4 s后開始出現偏差，影響到后續計算的正確性。在滾轉方向，分離后外掛彈體向機翼外側滾轉，在t=0.5 s之前滾轉角的計算和試驗值比較一致，由于x方向的轉動慣量較小(比其他兩個方向小1個量級)，氣動力估計的誤差很容易在這里得到放大，從而對計算結果造成污染。

圖25 外掛物姿態角隨時間變化情況

圖26 外掛物角速度隨時間變化情況

結合數值模擬方法，本文認為空間離散和時間離散的誤差來源于如下3個方面：① 重疊網格隱式裝配算法中，為簡明計，沿著挖洞邊界僅延拓了一層重疊單元，各部件網格間的物理信息交換量略顯不充分；② 雙時間推進過程中，限制器造成的數值解污染在一定程度上得以累積，影響了后期數值模擬的精度；③ SA湍流模型經驗參數的選取欠佳，影響了RANS方程黏性項的離散精度。今后需繼續研究重疊邊界附近的高精度插值技術；同時，不斷提高流場解算器的離散精度，從而在整體上降低CFD仿真過程中產生的誤差。

4 結 論

本文基于網格節點的壁面距離參數，構造了一種自動化的并行重疊網格隱式裝配算法，同時使用集合論對該算法的并行化過程進行了詳細地描述。網格組極小內部-外部盒子、盒子切割方法、初篩+確認兩步分析法、二叉樹排序-查找等技術的綜合運用，降低了重疊裝配算法的并行通訊壓力，使之能夠適應多體相對運動時復雜非定常流場的數值模擬。數值計算結果表明，該重疊裝配算法具備了較高的計算效率與魯棒性，能夠輔助實現針對外掛物分離的非定常流場準確模擬。

下一步工作內容包括兩方面：一是將自適應笛卡爾網格融入到當前的重疊裝配框架中，進一步拓展其工程應用范圍；二是繼續優化初篩技術，提升大規模重疊網格的并行裝配效率。