飛行控制律對體自由度顫振特性影響試驗

雷鵬軒，余立，陳德華，呂彬彬,*

1. 中國空氣動力研究與發展中心 空天技術研究所，綿陽 621000

2. 中國空氣動力研究與發展中心 高速空氣動力研究所，綿陽 621000

飛翼布局飛行器在氣動升阻比、隱身性能、結構效率等3個方面具有先天的優勢，已成為下一代軍事飛行器平臺的首選布局形式。為了充分發揮結構重量優勢，新一代飛翼飛行器多采用輕質復合材料，使其具有明顯的結構柔性，特別是一些大展弦比飛翼飛行器，其結構彈性振動一階固有頻率僅1 Hz或更小，另一方面飛翼飛機為無尾布局，俯仰轉動慣量小，縱向短周期運動模態頻率高，因此極易發生彈性振動模態與剛體短周期模態耦合，在遠低于設計限制的飛行速度下發生一種動力學失穩現象，造成結構破壞與飛行器墜毀[1-2]。這種由于剛體運動參與而造成的氣動彈性失穩現象被稱為體自由度顫振(Body Freedom Flutter, BFF)。

2003年美國空軍研究實驗室(Air Force Research Laboratory, AFRL)發起了SensorCraft項目[3]。項目中洛·馬公司提出了一款飛翼布局無人機SC005，經研究發現體自由度顫振成為限制該飛機包線的主要制約[4]。2007年洛·馬公司在NASA蘭利研究中心TDT風洞中開展了樣機SC006的體自由度顫振風洞試驗，詳細地研究了體自由度顫振現象，檢驗了顫振抑制控制律的有效性[5]。2010年AFRL聯合洛·馬公司提出了建立X-56A飛行演示平臺計劃(Multi-Utility Technology Testbed, MUTT)[6-8]，其目的之一就是采用飛行試驗研究體自由度顫振，發展氣動彈性力學/飛行力學綜合控制技術(Integrated Flight and Aeroelastic Control, IFAC)，目前該項目仍在繼續。2015年美國明尼蘇達大學開展了飛翼飛機(mAEWing1, mAEWing2)的體自由度顫振研究[9-10]，分析了該無人機在開環與閉環控制下的穩定性[11-12]，并于2017年6月完成了體自由度顫振及其抑制飛行演示驗證試驗[13]。目前國外關于體自由度顫振及其抑制技術的研究逐漸成為一個熱點。

在國內，2017年西北工業大學谷迎松等開展了彈性繩支撐下的平板外形全模飛翼體自由度顫振風洞試驗[14]。北京航空航天大學黃超等開展了半模模型的體自由度顫振及其主動抑制風洞試驗研究[15-16]。相比于國外，目前國內關于體自由度顫振的研究剛剛起步，研究對象多以開環模型為主，并不考慮飛行控制律的影響。

飛行控制系統是真實飛機必不可少的一部分，對于傳統的彎扭耦合顫振問題可以忽略，但對于體自由度顫振問題，顫振發生時飛機剛體俯仰姿態將劇烈變化，隨之而來的姿態保持控制必不可少。有研究表明飛行控制律會顯著影響體自由度顫振特性[4]，國內已開展過計算研究[17]，但還未開展試驗與計算的綜合研究。鑒于此，本文開展了飛行控制律對飛翼飛機體自由度顫振特性的影響研究，針對自主設計的顫振試驗模型開發了相應的俯仰姿態保持控制律，通過風洞試驗與頻域計算獲得了不同剛體自由邊界條件下的開環/閉環體自由度顫振特性，研究了閉環增益對體自由度顫振特性的影響規律，并簡要分析了影響機理。

1 試驗與計算方法

1.1 模 型

模型外形為中等展弦比飛翼外形，參考了目前體自由度顫振問題研究的主流平面外形(圖1)。該平面外形分為機身段、翼身融合段與外翼段3段，半模展長為1.527 m，占試驗段84%。外翼段共有3片舵面，單片舵面寬0.07 m，長0.37 m。

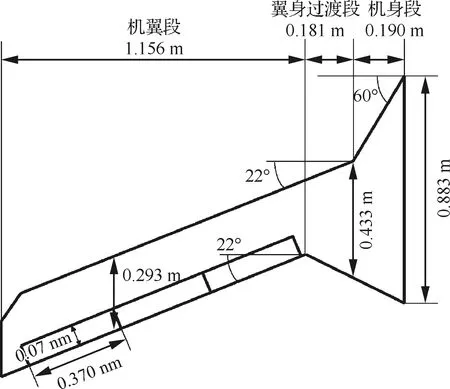
圖1 模型平面外形

模型結構為自主設計，采用了與真實飛機相同的梁架蒙皮式結構布局[18]，如圖2所示。模型分為機翼與機身兩大部分：機身蒙皮采用碳纖維布鋪層，機翼蒙皮采用玻璃纖維布鋪層，機翼梁與翼肋采用航空層板制作，舵面及小翼采用碳纖維布包裹，泡沫填充。

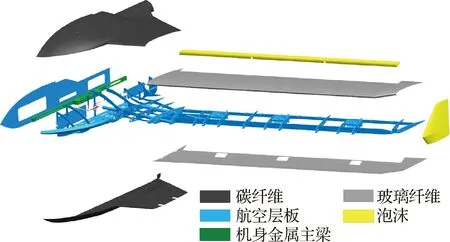
圖2 模型內部結構與材料

針對實物模型建立了相應的有限元模型，如圖3所示。首先對有限元模型的質量進行了修正。裝配前對模型的各部件進行稱重測量，以此在有限元模型中做相應修正，如表1所示。裝配好的模型重4.49 kg。俯仰轉動慣量并未實際測量，而是在質量修正的基礎上通過有限元模型核算，約為0.356 kg·m2。

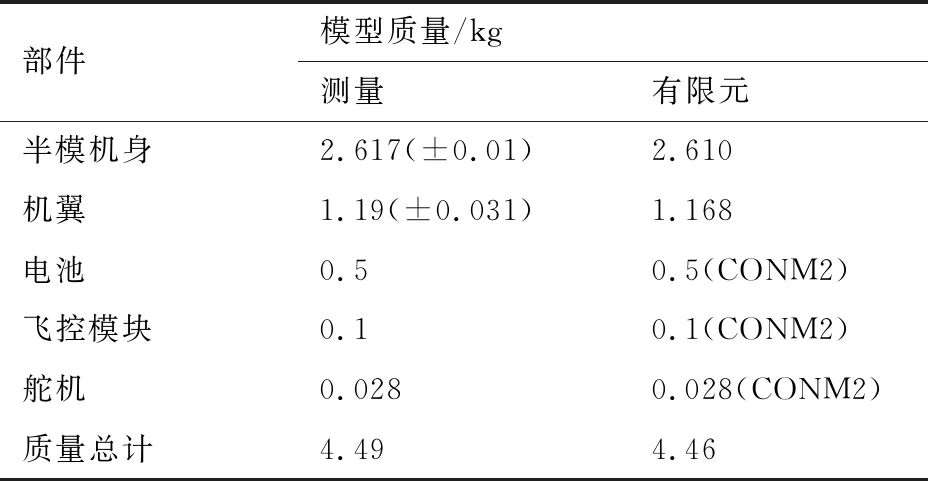
表1 實測模型部件與修正后的有限元模型質量

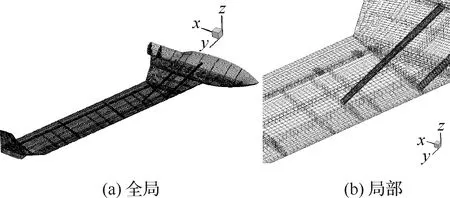
圖3 有限元模型

其次，對有限元模型的動力學特性進行了修正。在風洞安裝狀態下開展了地面振動試驗，使用PolyMax方法[19]進行模態參數識別。基于試驗結果，對有限元模型進行了修正，表2給出了前三階彈性模態頻率的對比，可見修正后的有限元模型能較準確地反映出模型實物的動力學特性。

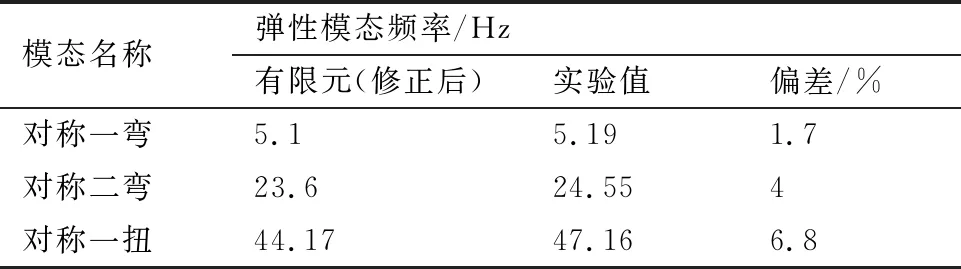
表2 地面模態試驗結果

1.2 風洞與試驗設備

風洞為中國空氣動力研究與發展中心的1.8 m×1.4 m低速風洞，閉口試驗段長5.8 m，空風洞最高風速105 m/s，閉口試驗段湍流度小于0.08%。模型側壁水平安裝(圖4)，模型可繞側壁上的支撐轉軸做俯仰自由轉動。

圖4 模型安裝狀態

模型與支撐轉軸采用螺釘連接。通過四顆螺釘將模型機身主梁壓緊在支撐轉軸上(圖5)，主梁上開有兩條“1”型槽，用來調節支撐轉軸與模型的裝配位置。俯仰支撐轉軸采用雙軸承支撐。在洞壁外側安裝有俯仰轉軸定位卡鉗(圖6)，采用氣缸推動，體自由度顫振出現時上頂卡鉗，鎖死俯仰自由度，模型會退出顫振，確保試驗過程中風洞和模型安全。

圖5 主梁與轉軸連接形式

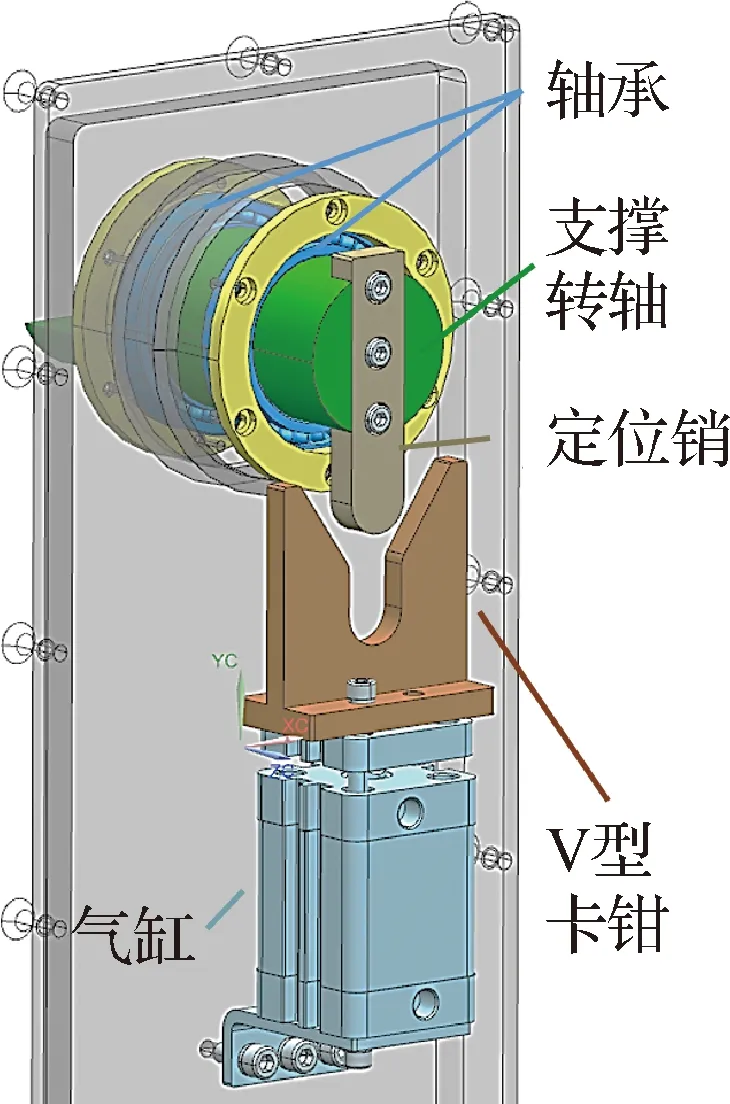
圖6 俯仰支撐轉軸與“V”型卡鉗

采用應變片和加速度傳感器測量模型的動態響應，采樣率200 Hz。加速度傳感器和應變片分別安裝在外翼的翼梢和翼根。模型機身前部安裝有空速管，用于測量風洞風速。模型內部配備有一套飛行控制系統用于模型俯仰姿態保持控制及采集記錄模型俯仰角，采樣率為25 Hz。飛控系統安裝于機身內部半模對稱面靠近質心位置處。其中俯仰角及角速度由內置于飛控系統的慣性測量單元測量，型號為ADIS16488。

1.3 俯仰姿態保持控制律

俯仰姿態保持控制采用俯仰角和俯仰角速度為反饋，根據不同的來流風速和目標俯仰角，通過調整外翼舵面，使模型保持預定的俯仰姿態。具體的控制律框圖如圖7所示。圖中αD表示目標俯仰角，α和q分別表示實測俯仰角和實測俯仰角速度。Airspeedscaler表示空速縮放系數，KC、KP、KI、KD為4個控制器參數，δ為輸出的目標舵偏角。俯仰姿態控制時，外翼的3片舵面共同偏轉，各舵面偏轉角度權重相同。

1.4 計算模型

顫振頻域計算中非定常氣動力采用偶極子網格法(Doublet Lattice Method, DLM)計算，氣動面網格劃分如圖8所示。采用P-K法求解，馬赫數Ma=0.1，空氣密度1.145 kg/m3。飛行控制律采用傳遞函數模型建模。為簡化計算模型，建模時采用俯仰角測值的一階微分代替俯仰角速度測值，即q(s)=sα(s)。令目標俯仰角為0°，則e(s)=-α(s)。將俯仰姿態保持控制律轉化為典型的單輸入單輸出PID控制器(圖9)。結合圖7的控制律框圖，各環節的傳遞函數模型為

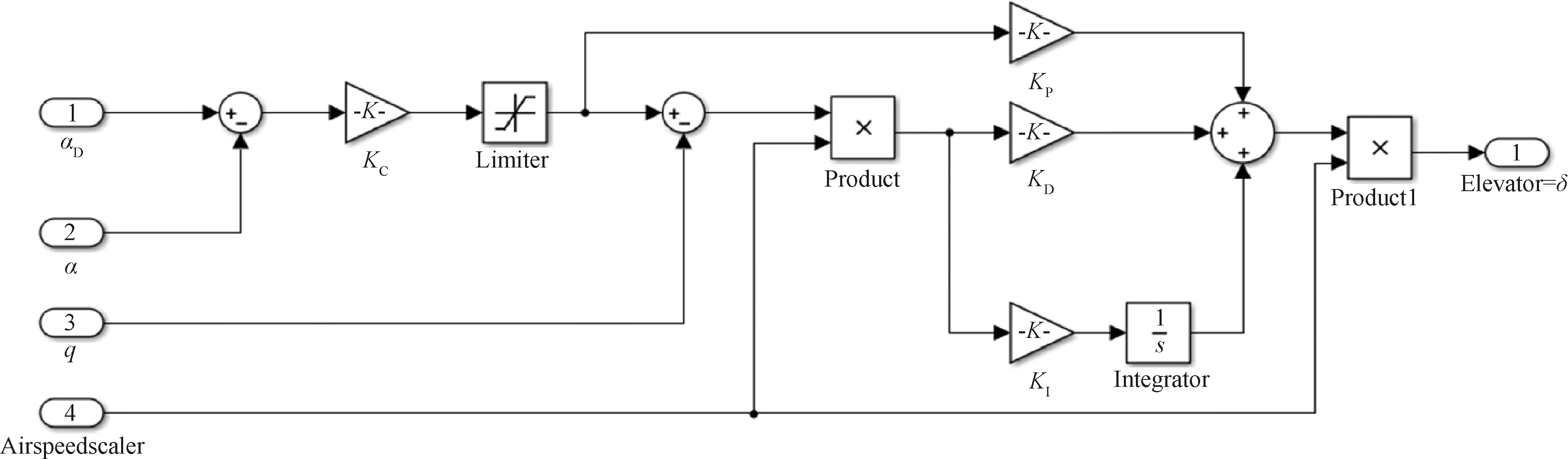
圖7 俯仰姿態保持控制律框圖

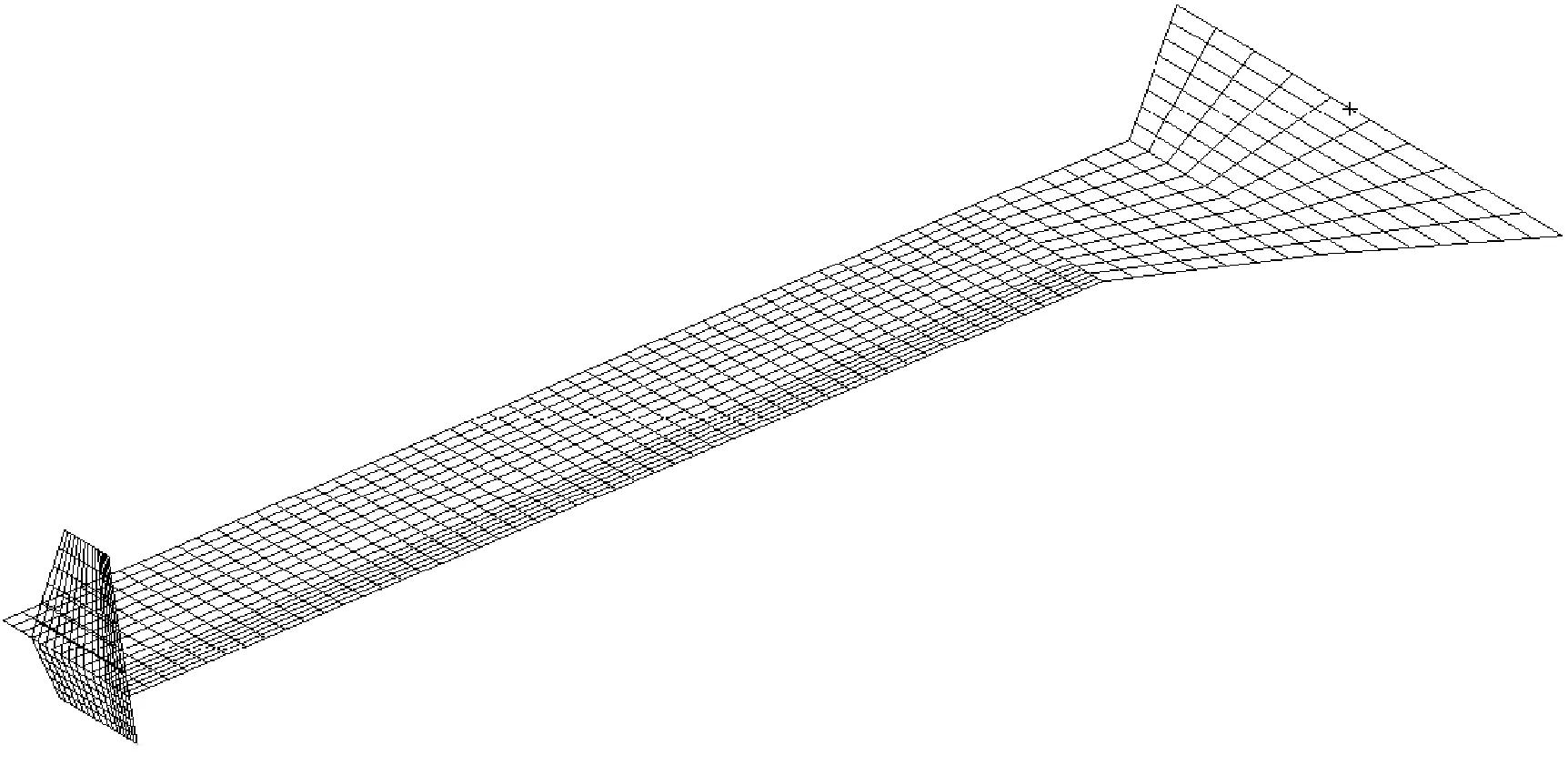
圖8 氣動面網格

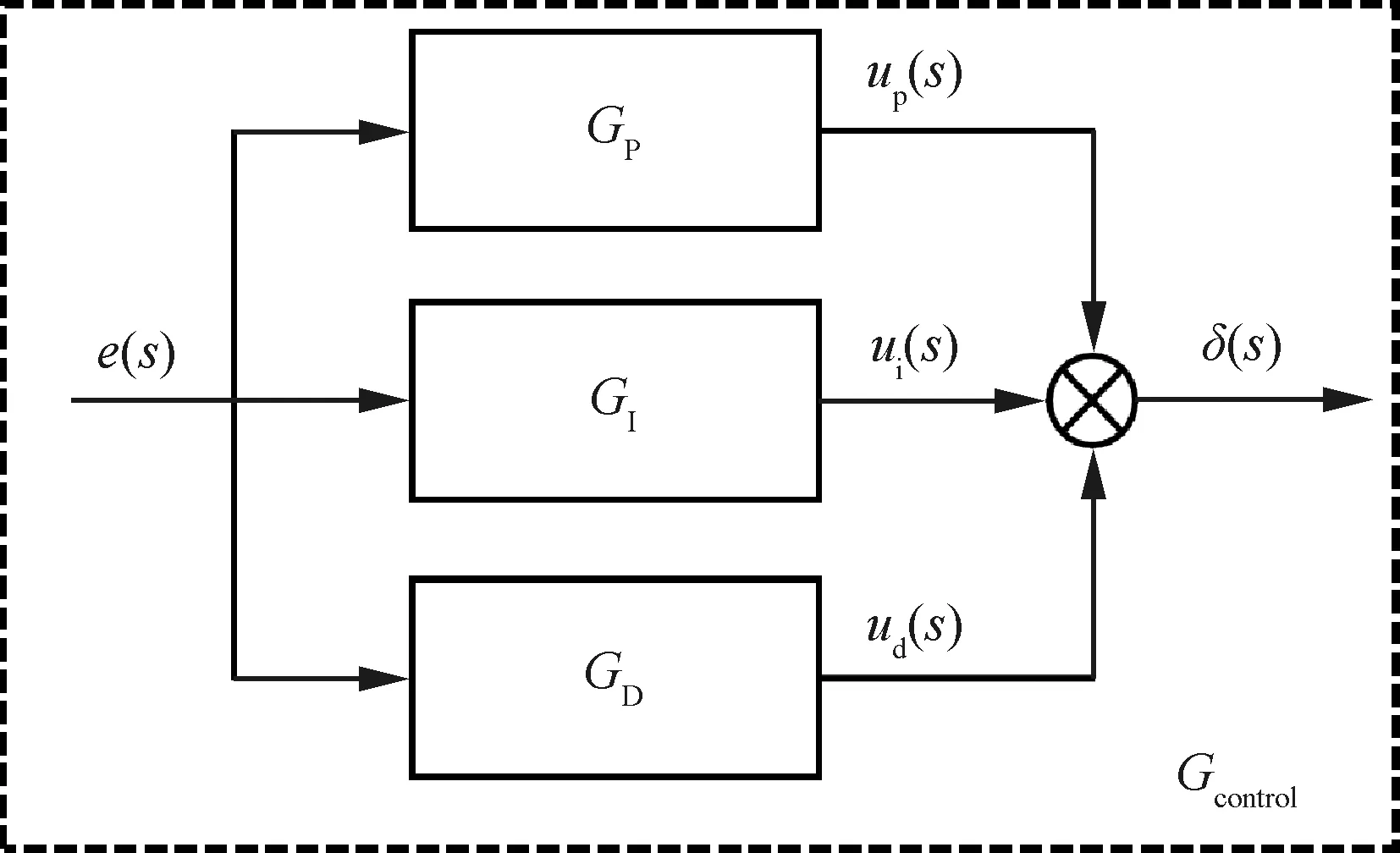
圖9 計算模型中使用的俯仰姿態保持PID控制器

Gcontrol(s)=GP(s)+GI(s)+GD(s)

(1)

GP(s)=KC·KP·KAirspeedscaler

(2)

(3)

(4)

此外，在氣動伺服彈性模型中還考慮了舵機模型和飛控系統的數據處理時間以及拉桿等機械結構響應滯后造成的時間遲滯影響。舵機的傳遞函數模型如式(5)所示。系統時滯為100 ms，采用二階Pade近似，如式(6)所示。最終氣動伺服彈性模型的方框圖如圖10所示，包含了飛行控制律、舵機模型、系統時滯和開環氣動彈性系統。

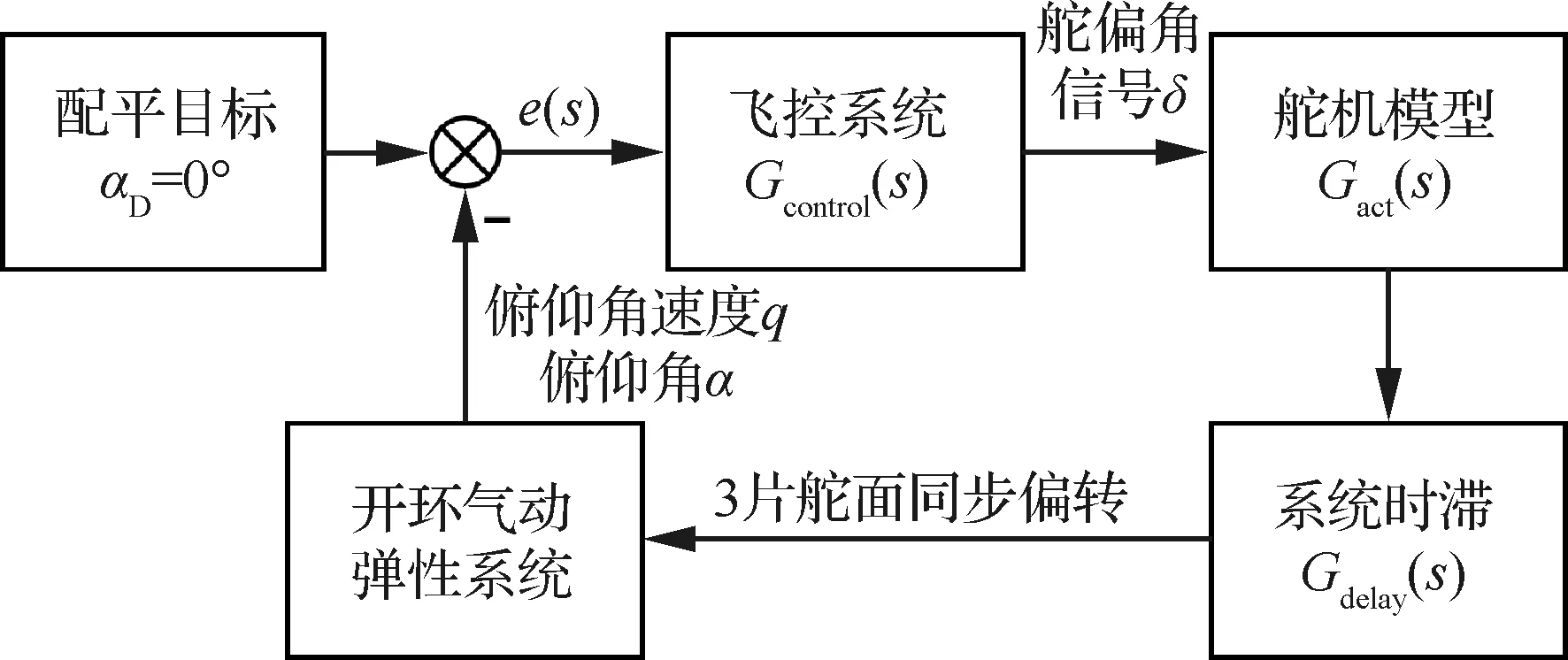
圖10 氣動伺服彈性模型方框圖

(5)

(6)

2 結果分析

顫振試驗采用風洞紊流激勵，試驗時風洞風速按階梯逐漸增加，通過直吹顫振獲得顫振特性參數。在此方法上，改變控制律參數，開展飛行控制律對體自由度顫振特性影響的試驗研究，同時針對不同試驗狀態開展頻域計算，進一步說明試驗獲得的影響規律。

試驗模擬了兩種剛體自由邊界條件：支撐轉軸位于質心位置和支撐轉軸前于質心位置。其中支撐前移狀態能夠在一定程度上模擬俯仰和沉浮兩個剛體自由度的影響，使模型的模態特性更接近剛體自由-自由對稱邊界情況(圖11)，該狀態著重于檢驗俯仰姿態保持控制律和計算模型的有效可靠；而質心位置支撐狀態僅模擬剛體俯仰自由度，著重于開展開環及不同增益下的閉環顫振特性風洞試驗研究。

圖11 支撐軸前移狀態

2.1 支撐軸前移狀態

首先對于支撐軸前移狀態可同時模擬俯仰和沉浮兩個剛體自由度，使模型的模態特性更接近剛體自由-自由對稱邊界情況做簡要說明[15]。如圖12所示，當轉軸不支撐在質心位置時(位于圖中x′)，模型繞支撐軸的轉動將包含俯仰和沉浮兩個形式的運動。通過合理的選定支撐轉軸前移距離l，可以實現俯仰、沉浮兩個自由度的模擬。

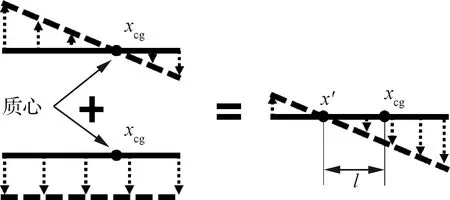
圖12 剛體沉浮和俯仰運動的疊加

具體來說，僅考慮俯仰和沉浮兩個剛體自由度的動力學方程：

(7)

式中：M為模型質量；R為模型俯仰慣量回轉半徑；Q為速壓；S為參考面積；CL為升力系數；xac為質心到焦點距離；質心在前為正。

當發生顫振時，兩個剛體模態做簡諧振動，設解的形式分別為：Zeiωt，Θeiωt，其中Z與Θ分別表示沉浮與俯仰剛體簡諧振動的幅值，ω為簡諧振動頻率。假設兩剛體運動幅值滿足Z=lΘ，代入方程可得

(8)

對比式(8)的兩行，若同時成立可得

l=-R2/xac

(9)

式中：負號表示質心在后，當x′點距質心的距離l滿足式(9)時，飛機在氣動力作用下的沉浮俯仰運動相當于繞x′做俯仰運動。

針對本文模型，表3給出了兩種邊界條件下前三階主要模態頻率對比，可見模態頻率非常接近。最大偏差不超過1.7%。圖13給出了兩種邊界條件下的模態振型有限元分析結果。可見支撐前移狀態的俯仰模態振型基本與自由-自由狀態的俯仰加沉浮模態振型接近，同時兩種支撐方式的一彎模態振型基本相同。

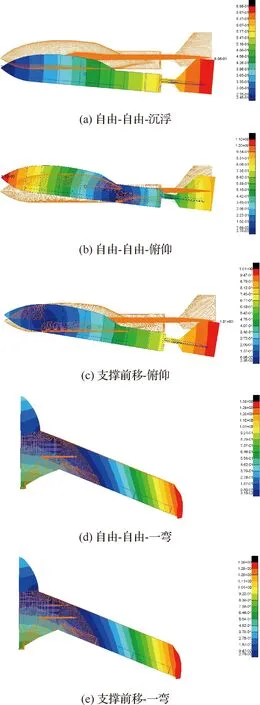
圖13 支撐前移與自由-自由狀態模態振型

表3 支撐前移與自由-自由狀態模態頻率對比

基于上述分析，本文采用支撐軸前移的方式開展了俯仰沉浮自由狀態的風洞試驗。試驗首先是驗證俯仰姿態保持控制律的有效性，其次通過對比閉環試驗結果與開環/閉環計算結果初步分析控制律對體自由度顫振特性的影響規律，同時檢驗氣動伺服彈性計算模型的可靠性。

試驗過程如圖14所示，剛開始試驗時，由于重力力矩的作用，模型位于最大限位位置，此時俯仰角約為13.4°。

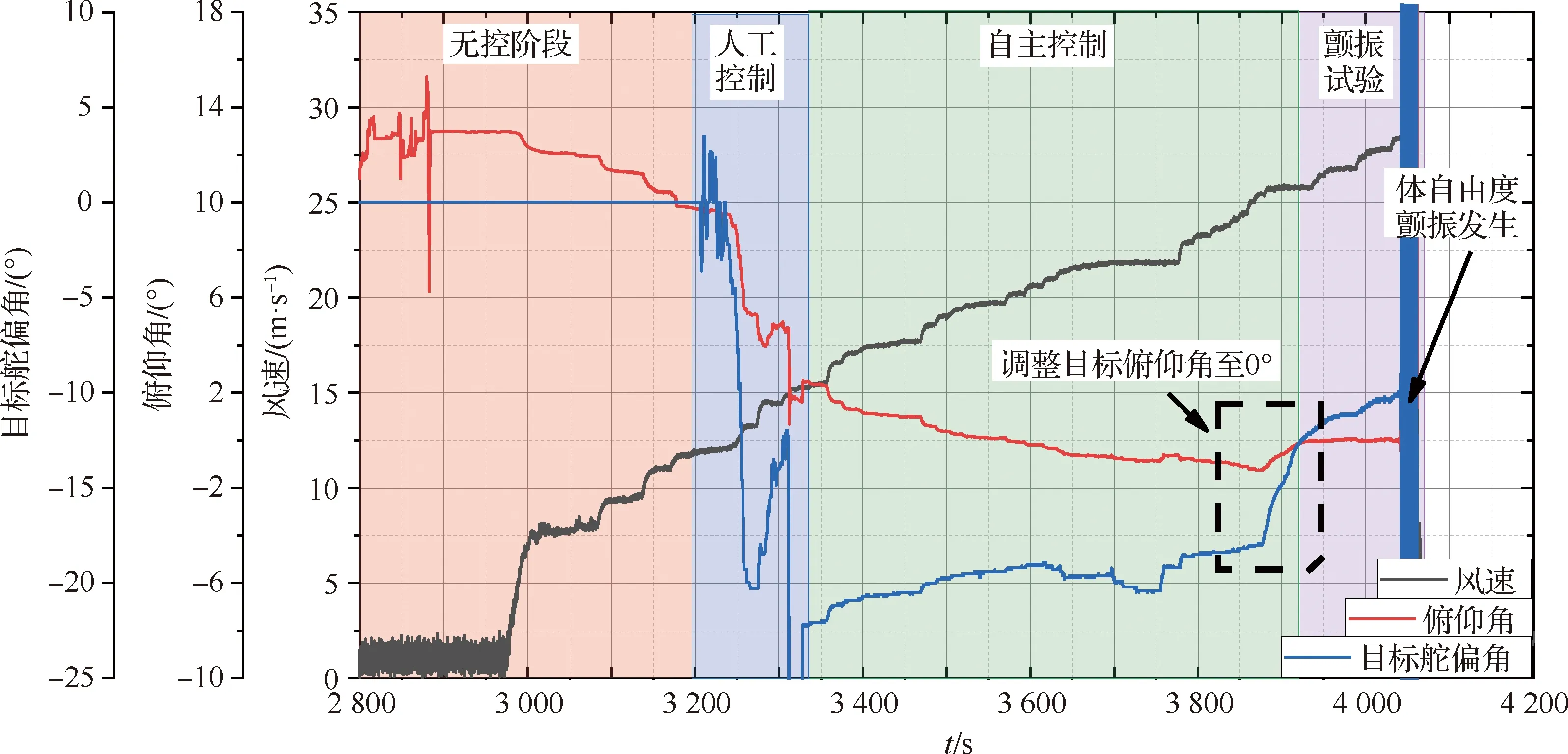
圖14 支撐軸前移狀態試驗結果

在無控階段，隨著風速逐漸增大俯仰角降低，但由于風速仍然較低，舵效不足，打舵至最大位仍無法配平力矩，因此先保持飛控開環。

隨著風速繼續增大，首先通過人工控制，調整模型姿態，將模型拉起。當風速到達15 m/s后，進入自主控制階段。可見隨著風速增大，模型俯仰角由正向負降低，舵偏角相應的由負向正逐漸增加，俯仰姿態保持控制律能通過自主調節舵偏角來實現模型縱向姿態的調整與保持。

當風速到達25.7 m/s時，進入顫振試驗階段，調整目標俯仰角為0°。隨著風速繼續增大至28.3 m/s，體自由度顫振出現。圖15給出了體自由度顫振發生時4個采集通道振動信號的頻率響應結果，顫振發生時的頻率約為3.7 Hz。

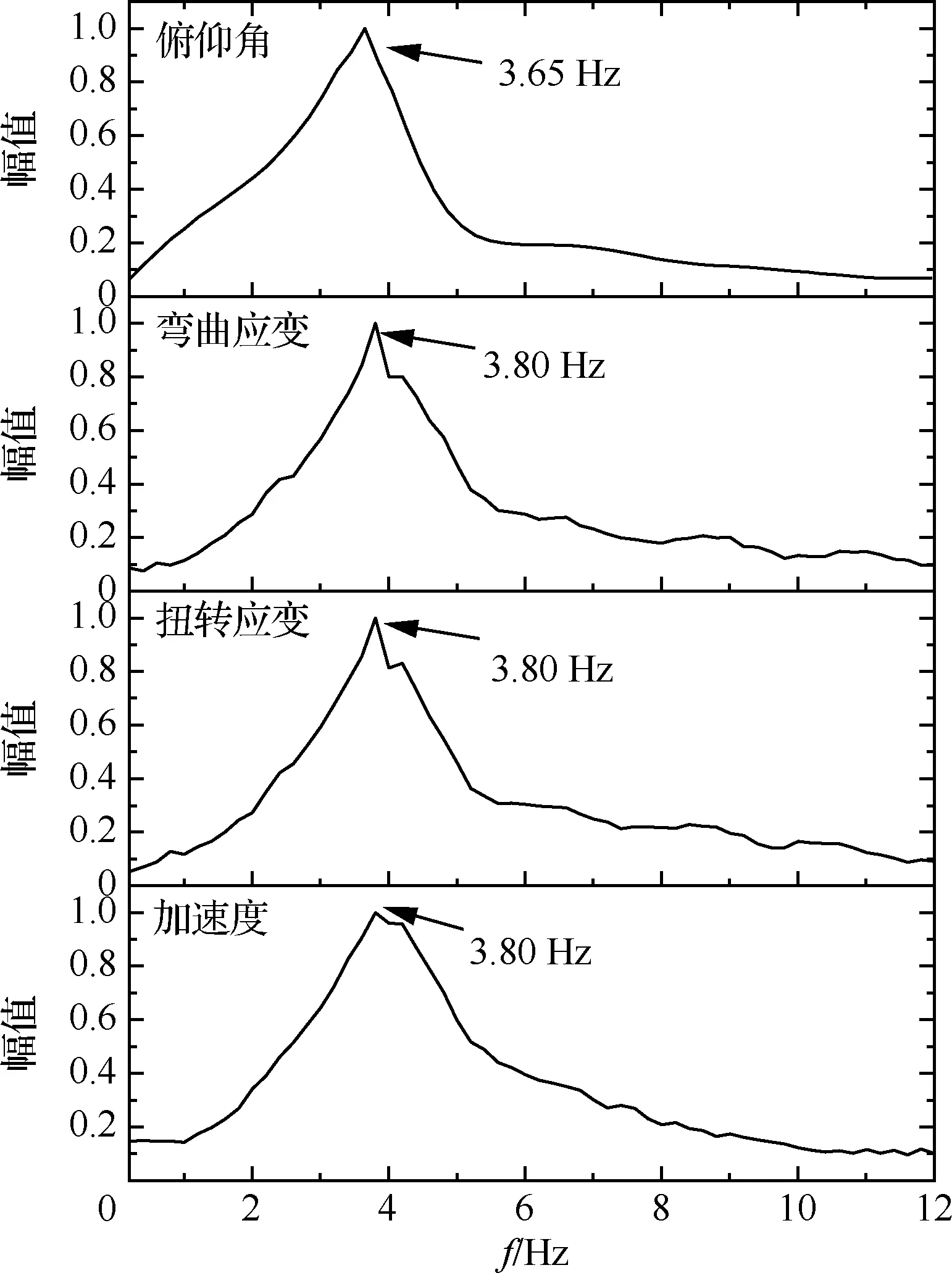
圖15 頻域響應試驗結果

采用頻域計算對控制律的影響作進一步分析，圖16給出了開環與閉環模型的顫振計算結果對比，分別為阻尼比g和模態頻率f隨速度V的變化規律。從圖16可以看出，開閉環前后的體自由度顫振發散模態均為俯仰模態，但閉環控制明顯改變了模態阻尼的原有走勢，閉環后的俯仰模態阻尼顯著降低。計算的開環顫振速度為39.6 m/s， 顫振頻率為5.04 Hz，明顯高于試驗獲得的閉環顫振速度28.3 m/s和顫振頻率3.70 Hz。計算的閉環顫振速度28.9 m/s與頻率3.44 Hz，與試驗吻合較好。

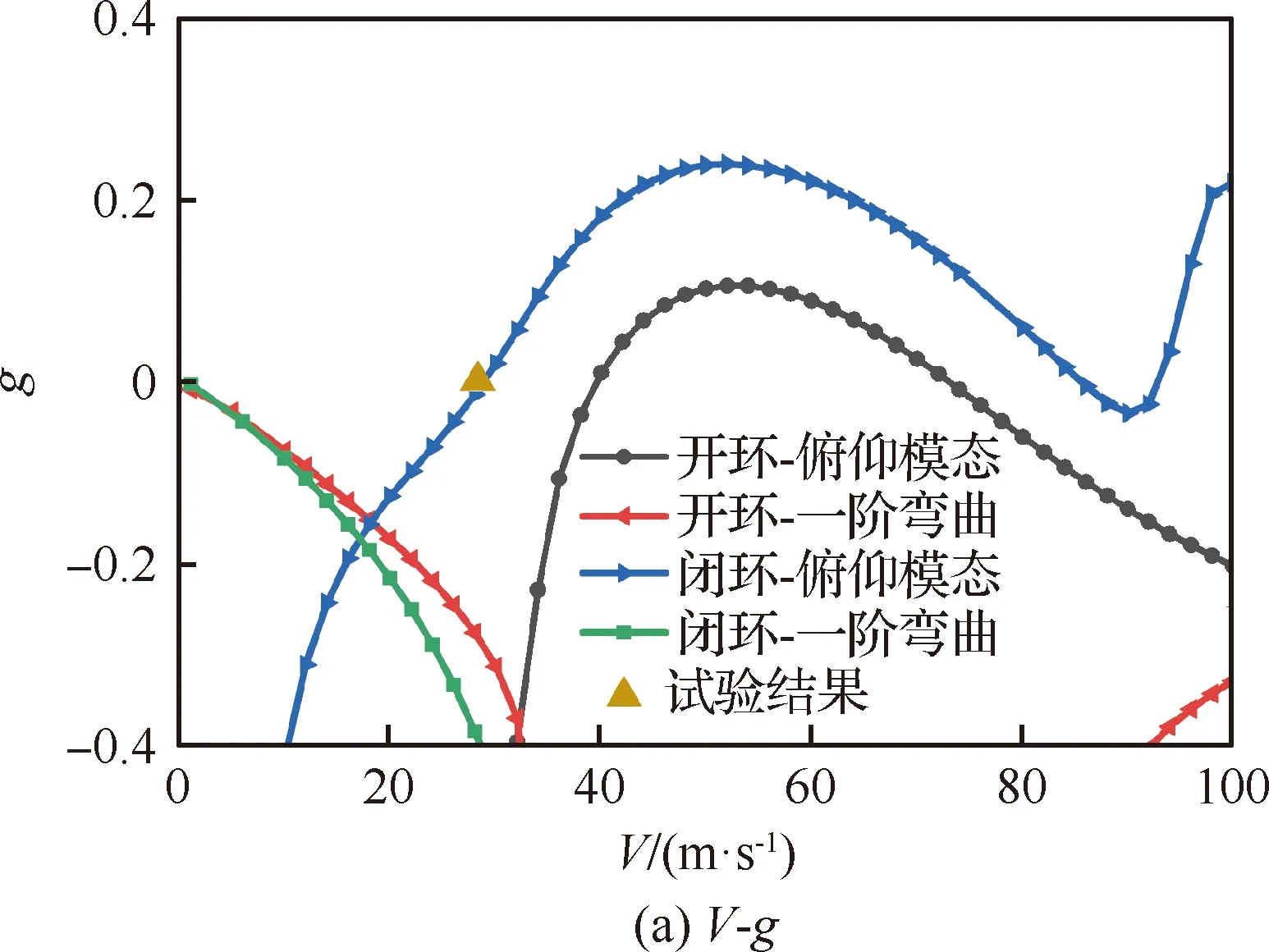
圖16 開/閉環顫振V-g和V-f圖

通過支撐前移狀態試驗一方面驗證了俯仰姿態保持控制律的有效性，可實現俯仰角的自主控制，檢驗了所建立的氣動伺服彈性計算模型的可靠。另一方面試驗結果說明體自由度顫振特性受控制律影響顯著，開環與閉環模型的顫振特性完全不同。

2.2 質心位置支撐狀態

由于支撐前移時必須引入控制律，在不同風速下保持模型姿態，因此難以通過試驗對比開環閉環前后的顫振特性變化。當支撐轉軸位于質心時，模型僅存在剛體俯仰自由度。對于靜穩定的模型，無需舵面參與，在開環狀態僅通過模型俯仰角即可實現俯仰力矩的配平，便于開環閉環試驗對比，以及控制律參數影響規律研究。因此本文在質心位置支撐狀態下開展了開環及閉環不同比例回路增益KP下的風洞試驗。

首先對質心位置支撐狀態下的開環顫振特性進行了計算，說明該狀態下同樣會發生體自由度顫振。圖17給出了開環狀態顫振計算結果，在此狀態下同樣發生了由俯仰模態和一階彎曲模態耦合造成的體自由度顫振，且發散模態分支同樣為俯仰模態。此時的顫振特性與支撐前移時有所區別，顫振速度為23.7 m/s，顫振頻率為1.95 Hz，較支撐前移狀態偏低。由于控制律中并不包含沉浮運動相關變量，因此這并不會改變飛行控制律對體自由度顫振特性的影響機理。

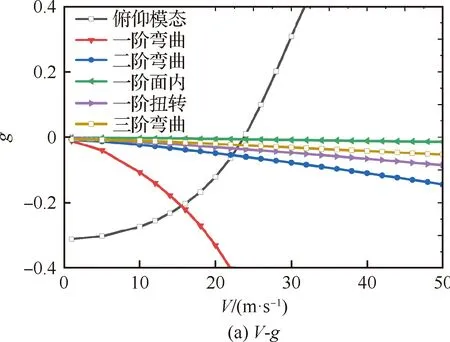
圖17 沉浮運動約束時顫振計算結果

根據上述分析，開展了質心位置支撐狀態的閉環顫振特性風洞試驗研究。圖18給出開環與不同比例環節閉環增益KP下的顫振臨界風速對比，其中體自由度顫振發生時由于俯仰姿態大幅運動，空速測值瞬間降低。以此為標志從圖中可見，隨著KP增大，顫振速度逐漸減低。圖19給出了開環以及不同KP下的頻域響應試驗結果，可見閉環顫振頻率較開環增大，但隨著KP增大基本保持不變。

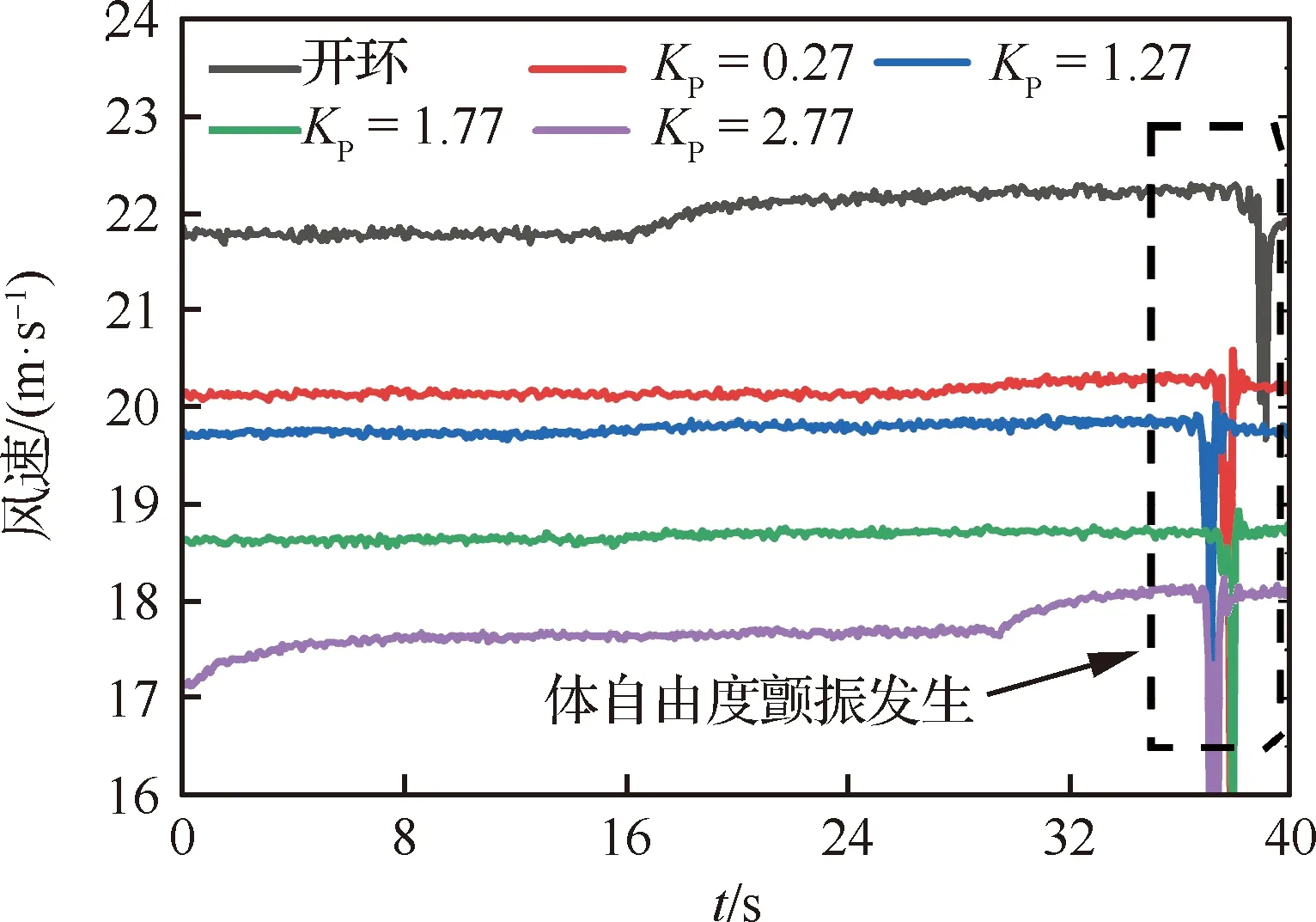
圖18 不同閉環增益下的顫振臨界速度

圖19 不同閉環增益下的頻率響應結果

采用頻域計算對控制律的影響作進一步驗證。圖20、圖21給出了不同增益下的顫振速度和頻率的計算結果及其與試驗結果的對比。計算結果同樣獲得了與試驗一致的閉環控制的影響規律。在量值上計算與試驗吻合較好，計算獲得的顫振速度隨KP增加降幅更大。

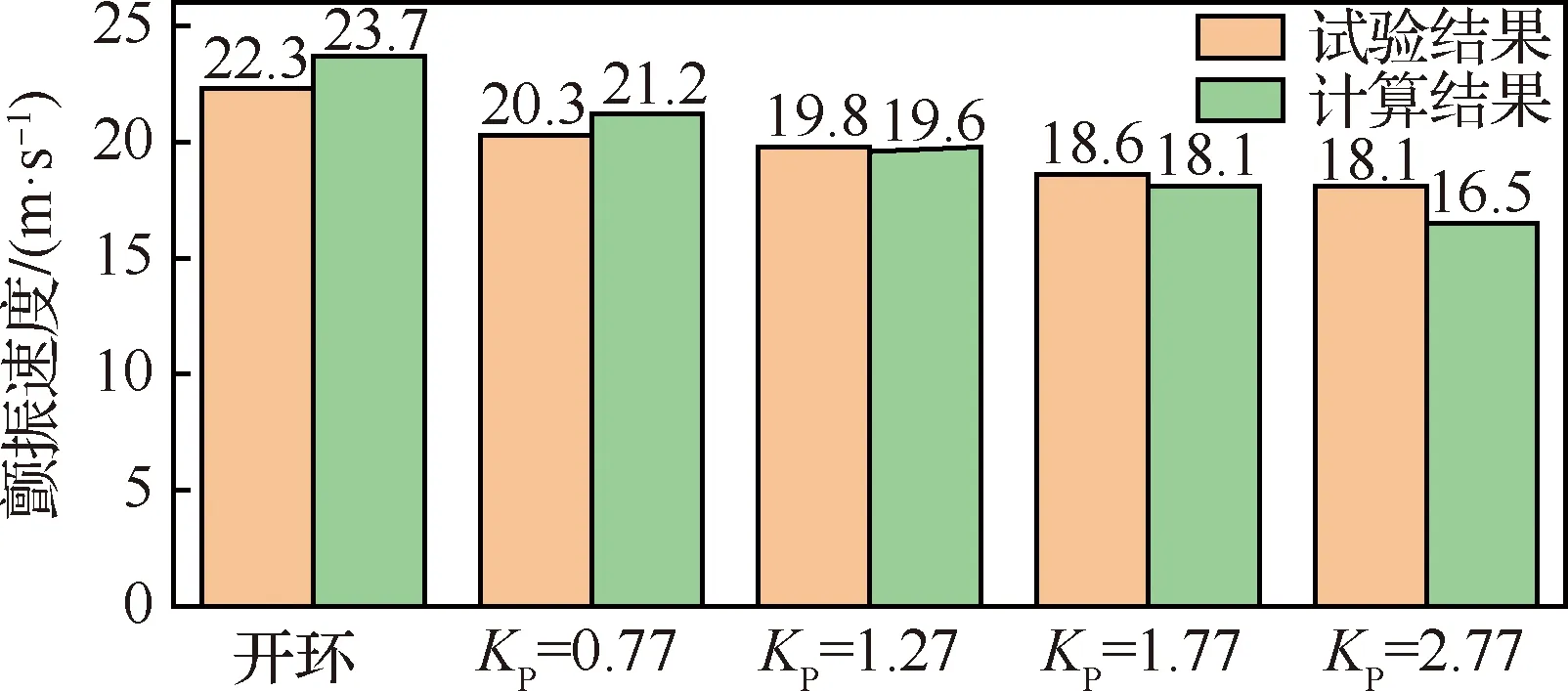
圖20 不同閉環增益下的顫振速度計算結果與試驗結果對比

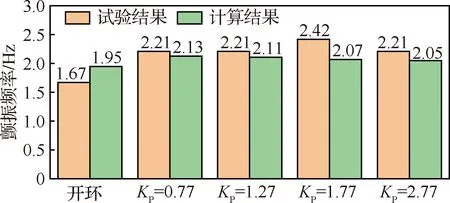
圖21 不同閉環增益下的顫振頻率計算結果與試驗結果對比

對于俯仰姿態保持控制律影響機理的簡要分析如下。

一般來說，俯仰角傳動比增大會加快調節時間、減小穩態誤差，但過大會使系統不穩定。俯仰角速度傳動比增大，會加大俯仰阻尼、提高系統平穩性[20]。圖22給出了不同閉環比例回路增益和微分回路增益下的控制律的相頻特性曲線，可見隨著KP增大以及KD減小，PID控制器相位超前減小，標志著俯仰角傳動比增加，俯仰角速度傳動比減小，因此控制響應更快，但同時系統的俯仰阻尼降低，以致體自由度顫振速度降低。從試驗獲得的俯仰角發散曲線中也能發現，KP越大顫振發生越突然(圖23)。

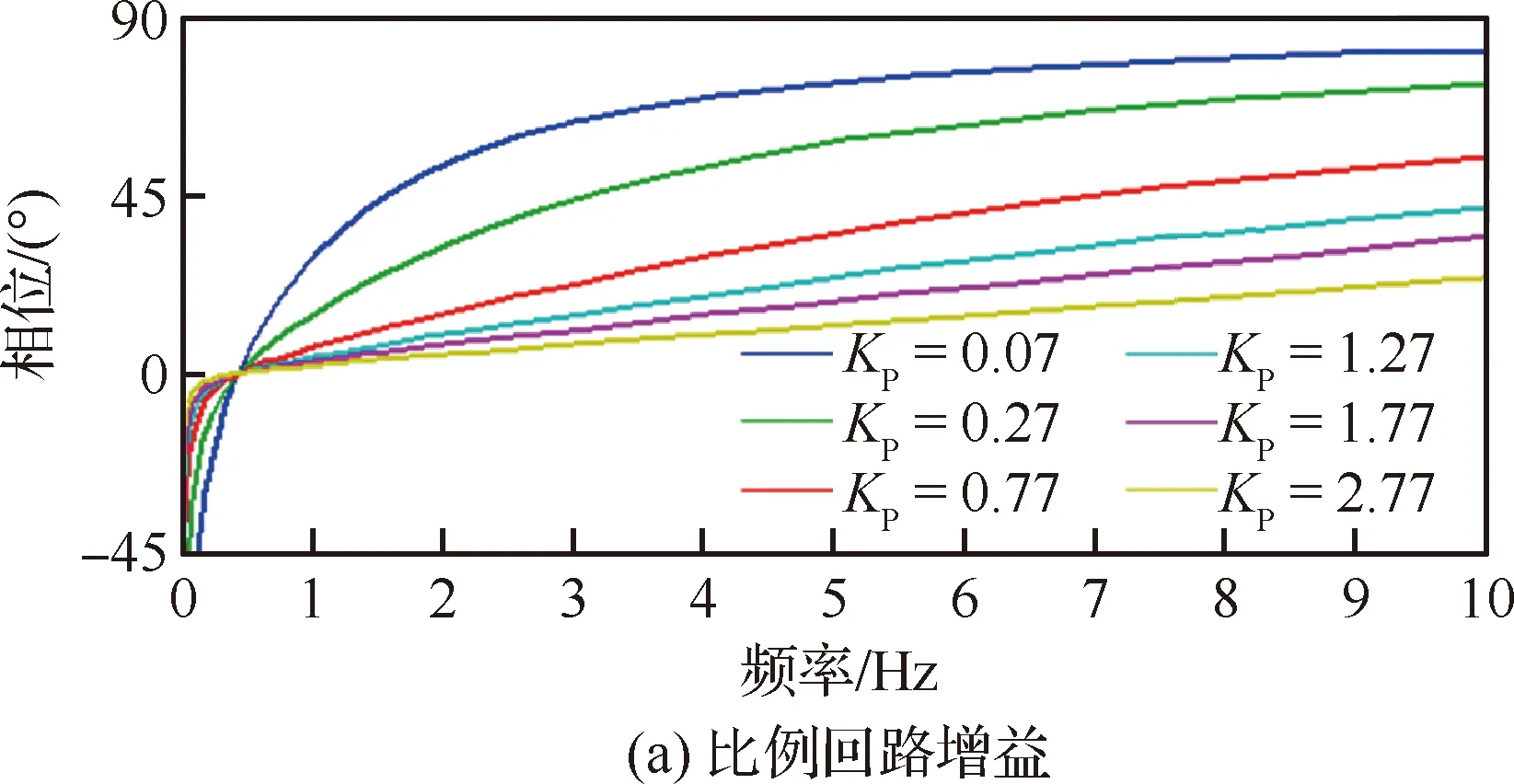
圖22 不同閉環增益下的PID控制器相頻特性

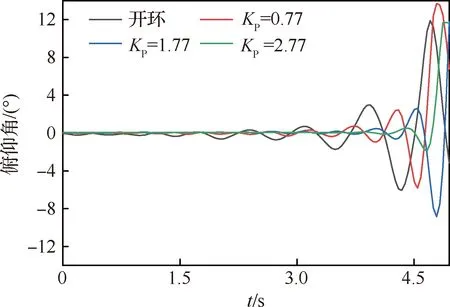
圖23 不同閉環增益下的俯仰角發散曲線

根據上述針對試驗結果的分析，從反方面推論可得：減小KP、增大KD將有利于顫振速度的提高。因此本文采用計算手段，分析了不同KP和KD下的顫振特性，圖24給出了不同KP下的俯仰模態分支阻尼變化規律。可見模態阻尼走勢的變化主要表現為平移變化，即降低KP整體增加了俯仰模態阻尼。當KP=0.07時，閉環顫振速度高于開環顫振速度，俯仰姿態保持控制律起到了顫振抑制的作用。圖25給出了不同KD下俯仰模態阻尼走勢的變化規律。可見隨著KD增大，顫振速度也會增大，但變化量值明顯小于KP的影響。從PID控制器的相頻特性曲線能看出，隨著KD增大，控制器相位增量越來越小，因此對顫振速度的影響也越來越小。當KD=0.20時，閉環顫振速度高于開環顫振速度，俯仰姿態保持控制律同樣起到了顫振抑制的作用。綜合KP和KD的變參計算分析結果表明通過設計飛機自身的飛行控制律，增大俯仰角速度傳動比，增加俯仰阻尼，能實現體自由度顫振的抑制。

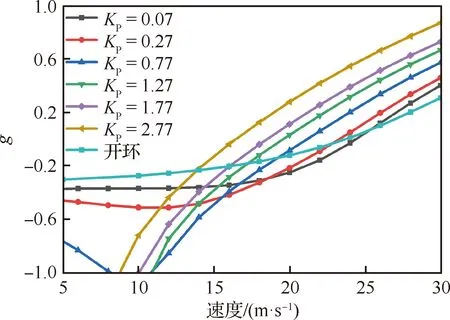
圖24 不同KP下的俯仰模態阻尼變化曲線

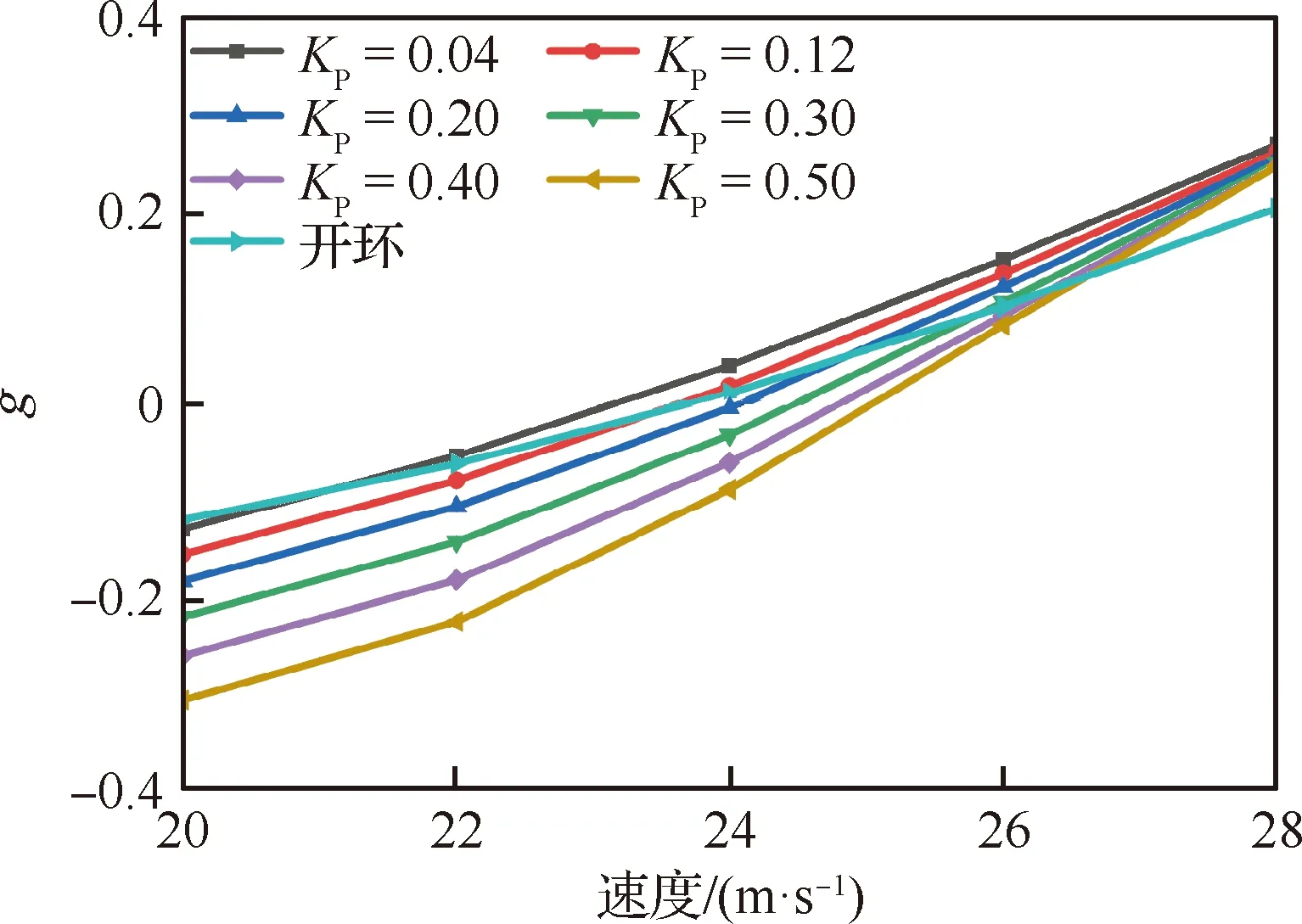
圖25 不同KD下的俯仰模態阻尼變化曲線

3 結 論

1) 經風洞試驗檢驗，本文所使用的俯仰姿態保持控制律合理有效，可實現模型俯仰姿態的自主控制。這是開展飛行控制律對體自由度顫振特性影響研究的基礎。

2) 風洞試驗與計算結果共同表明，體自由度顫振特性受飛行控制律影響明顯，在飛行器的體自由度顫振分析中不可被忽略。就本文試驗中的控制律與模型而言，閉環后顫振速度降低，顫振頻率提高，且比例回路增益越大，顫振速度越低，顫振發生的越突然，但此時顫振頻率基本保持不變，試驗結果與計算結果在規律和量值上吻合較好。

3) 俯仰姿態保持控制律影響機理研究表明，控制律主要通過改變俯仰氣動阻尼來影響體自由度顫振特性。以開環顫振速度為基準，較大的比例回路增益或較小的微分回路增益，使得俯仰角傳動比大，雖然系統響應速度較快，但閉環后降低了俯仰阻尼，應用此時的飛行控制律會導致閉環顫振速度降低；而比例回路增益較小或微分回路增益較大時，俯仰角速度傳動比大，飛控閉環后能起到增加俯仰阻尼、抑制體自由度顫振的作用。