亞聲速風洞可壓縮流體擾動模態分析

杜鈺鋒，林俊，王勛年，熊能

1. 中國空氣動力研究與發展中心 高速空氣動力研究所，綿陽 621000

2. 中國空氣動力研究與發展中心 空氣動力學國家重點實驗室，綿陽 621000

風洞試驗段的核心流區域是經過導流片、蜂窩器、阻尼網等整流裝置整流后風洞中流場品質最好的區域[1-4]，但盡管如此，進入風洞試驗段的自由來流仍然具有非定常特性。從理論上來看，自由來流擾動是由流場中各個物理量的脈動綜合導致的；而從實際的風洞結構來看，風洞運行過程中的驅動系統、加熱(冷卻)系統、閥門系統等均是自由來流擾動的源頭[5]。自由來流擾動會對風洞試驗結果的精度產生影響，致使風洞試驗結果產生誤差，風洞試驗結果誤差對于飛行器設計而言即意味著升力、阻力系數等氣動參數存在設計誤差，進而會導致飛行器載重量存在估算誤差，嚴重制約了飛行器的經濟性與安全性[6]。因此，對自由來流擾動進行精確量化評估就顯得尤為重要。

文獻[7]利用小擾動理論對流體力學基本方程進行了線性化處理，求解后發現自由來流擾動是由3種基本擾動模態疊加構成的，分別為：聲模態、渦模態及熵模態，且3種擾動模態的構成成分不盡相同。聲模態是由等熵狀態下的壓力脈動、密度脈動、溫度脈動及無旋速度脈動構成的；渦模態是由有旋速度脈動構成的；熵模態是由定壓狀態下的熵脈動、密度脈動與溫度脈動構成的[7-8]。

由于3種擾動模態的構成成分不同，其產生機制也不盡相同。一般來說，湍流邊界層是聲模態的主要來源，風洞中的蜂窩器與阻尼網等是渦模態的主要來源，流場中的非均勻溫度場是熵模態的主要來源。文獻[9]對超聲速風洞中3種擾動模態的產生機制進行了溯源研究，結果表明：渦模態與熵模態在流場中沿流線傳播，因此兩者的產生與風洞穩定段中的流動現象有關；而聲模態在流場中可跨流線傳播，因此聲模態的產生與風洞穩定段中的流動現象及試驗段中的邊界層有關。文獻[10-11]利用聯合模態分析方法分別對超聲速風洞與高超聲速風洞試驗段中3種擾動模態的量值進行了測量，通過對比分析可以發現，超聲速風洞與高超聲速風洞試驗段中聲模態均為最主要的擾動模態，在超聲速風洞試驗段中，由于風洞沒有采取加熱措施，渦模態的幅值要明顯高于熵模態，而在高超聲速風洞試驗段中，由于采取加熱措施引入了熵脈動，渦模態的幅值反而要明顯高于熵模態。通過對比可知，高超聲速風洞中的加熱裝置是熵模態的重要來源。

3種擾動模態不僅產生機制不同，其對流動現象的作用機理也不相同。文獻[12-13]指出，自由來流擾動中的有旋成分(渦模態)是引發邊界層轉捩過程中三維breakdown過程的誘因，而文獻[14]指出，自由來流擾動中的無旋成分(主要是聲模態)是觸發二維TS波初始幅值的主要因素。不同擾動模態對邊界層轉捩的作用機理存在差異，在邊界層轉捩的預測與控制中也存在不同的作用。

綜合以上分析可知：為了能夠精確定量分析不同擾動模態在風洞中的源頭并加以抑制，以提升風洞流場品質，提高風洞試驗結果精度，并且為了能夠精確定量分析不同擾動模態對流動現象的影響機理，需要對風洞試驗段中的不同擾動模態均進行量化評估。目前，亞聲速風洞可壓縮流速域在眾多客機、軍用運輸機、遠程戰略轟炸機、預警機及加油機等先進大型飛機的氣動力評估及氣動外形精細化設計中發揮了重要作用[15-17]，但正是由于其中的自由來流擾動模態沒有進行量化評估，導致無法精確量化試驗結果的精度。目前已有的研究成果絕大多數是針對超聲速與高超聲速風洞中自由來流擾動模態的研究[10-11,18-20]，亞聲速風洞可壓縮流速域的研究成果相對較少。

本文對亞聲速風洞中可壓縮流體在等熵條件下所包含的擾動模態進行了分析，對擾動模態求解方法及流場基本物理量聲、渦模態分量求解方法進行了理論推導，建立了應用熱線測速技術測量結果對其進行求解的理論關系。在馬赫數Ma= 0.3～0.7進行了流場品質測量試驗，利用以上理論關系對擾動模態及流場基本物理量聲、渦模態分量進行了求解，對其量值變化趨勢進行了分析，并利用蒙特卡洛模擬方法和不確定度傳遞公式對結果的不確定度進行了計算。結果表明擾動模態及流場基本物理量聲、渦模態分量及其變化規律合理，且不確定度量值遠小于對應變量的量值，驗證了求解方法的可行性，為亞聲速風洞擾動模態分析乃至流場品質評估提供了借鑒。

1 亞聲速風洞擾動模態理論推導

根據文獻[7]，有黏性、可壓縮、可導熱的氣體中存在3種不同的擾動模態：聲模態、渦模態、熵模態，分別服從3個準獨立的偏微分方程，以下將從流體力學基本方程出發對其形式進行推導分析。對以上氣體進行如下假設：① 該氣體是有常比熱比、常黏度系數、常熱導率的理想氣體；② 該氣體的Pr數為0.75[21]。根據動量守恒、能量守恒、連續性方程、理想氣體狀態方程，氣體的控制方程如下：

(1)

(2)

(3)

(4)

式中：ρ、v、p、μ、T、cp、κ、γ分別為氣體密度、速度、靜壓、動力黏度系數、靜溫、定壓比熱容、熱導率、比熱比；t為時間；Φ為黏性耗散項。

對以上方程描述的氣體繼續引入假設：③ 根據小擾動理論，p、ρ、T、v的脈動量遠小于其均值；④ 取隨體坐標系對以上方程描述的氣體進行分析，在隨體坐標系中，介質平均速度為0。

為了便于求解式(1)～式(4)，對其中部分變量進行無量綱化處理：

(5)

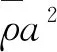
(6)

將式(6)代入式(5)可知：

(7)

理想氣體熵變化量方程為

(8)

式中：s為氣體的比熵；R為氣體常數。

對式(8)中的熵變化量進行無量綱化處理：

(9)

式中：σ為無量綱熵脈動。

利用式(7)、式(9)定義的無量綱變量及式(4)、 式(8)，對部分物理量進行無量綱化，結果如下：

(10)

(11)

利用以上無量綱結果及線化處理方法對控制方程(1)～方程(3)進行處理。動量守恒方程無量綱化及線化后結果為

(12)

式中：ν為運動黏度系數，ν=μ/ρ。

對能量守恒方程進行線化處理，可得

(13)

對式(13)保留小擾動量并進行無量綱化處理，可得

(14)

由式(7)、式(10)、式(14)可得

(15)

由Pr數定義及其假設與定壓比熱容cp與氣體常數R的關系，可得

(16)

(17)

整理式(6)、式(15)～式(17)，可得能量守恒方程無量綱化及線化后結果為

(18)

對連續性方程進行線化處理，可得

(19)

由式(11)與式(19)可得連續性方程無量綱化及線化后結果為

(20)

式(12)、式(18)、式(20)即為3種不同的擾動模態服從的引入一階小擾動后無量綱化且線化的控制方程組。利用以上結果可推導不同擾動模態服從的獨立控制方程。

對v取旋度，可得渦量ω：

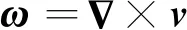
(21)

將式(21)代入式(12)中，可得

(22)

式(22)即為渦模態服從的獨立控制方程，說明渦模態與聲模態、熵模態無一階干擾。

對式(12)取散度，并結合式(18)、式(20)，可得

(23)

式(23)即為聲模態服從的獨立控制方程，說明聲模態與渦模態、熵模態無一階干擾。

對于亞聲速風洞的自由來流，可以認為是一維等熵流動[5, 22]，根據等熵關系式：

(24)

由式(11)與式(24)可知：在亞聲速風洞中，無量綱熵脈動σ=0。

根據以上結果可知：在亞聲速風洞中，聲模態定義為式(7)，渦模態定義為式(21)，兩者均服從由流體力學基本方程推導出的獨立控制方程；熵模態σ=0。由渦模態的定義式(21)，常規的脈動量測量手段難以對渦量場脈動進行準確測量。根據文獻[23]，可利用將平面聲波導致的無旋速度脈動從總速度脈動中扣除的思想來重新定義渦模態以便于測量求解，其定義為

(25)

式中：ω為渦模態；u為亞聲速風洞主流方向速度分量；Ma為馬赫數；φ為平面聲波傳播方向與風洞主流方向的夾角。

綜上所述，在亞聲速風洞中，聲模態P定義為式(7)，渦模態ω定義為式(25)，熵模態σ=0。

2 亞聲速風洞擾動模態求解方法推導

熱線測速技術由于其頻響高的優點，是風洞自由來流脈動量測量最常用的手段。由文獻[24]可知，利用變熱線過熱比方法可以對自由來流的質量流量脈動、總溫脈動及其相關量進行測量，以下將利用質量流量脈動、總溫脈動及其相關量作為已知量，對自由來流擾動模態及基本物理量聲、渦模態分量的求解方法進行推導。

2.1 擾動模態求解方法

質量流量脈動與密度脈動和速度脈動的關系為

(26)

式中：m為質量流量。

總溫脈動與靜溫脈動和速度脈動的關系為

(27)

式中：T0為總溫。

由式(4)可得理想氣體狀態方程脈動量形式為

(28)

由式(24)、式(26)～式(28)可求解出壓力脈動與質量流量脈動和總溫脈動的關系為

(29)

由式(7)和式(29)可知，聲模態與質量流量脈動和總溫脈動的關系為

(30)

由式(24)、式(26)～式(28)可推導出速度脈動與質量流量脈動和總溫脈動的關系為

(31)

由式(25)、式(29)、式(31)可知，渦模態與質量流量脈動和總溫脈動的關系為

(32)

2.2 流場基本物理量聲、渦模態分量求解方法

首先對速度脈動及總溫脈動的聲、渦模態分量進行求解，其關系式為

(33)

(34)

式中：下角標P代表聲模態分量；下角標ω代表渦模態分量。

(35)

對于平面聲波導致的聲擾動模態，其壓力脈動是速度脈動產生的原因。聲波傳播的聲阻抗方程為[25]

(36)

式中：ΔuP為壓力脈動導致的速度脈動。

由式(6)及式(36)可知：

(37)

將ΔuP在風洞主流方向上投影，結合式(24)與式(28)，可得

(38)

由式(35)與式(38)可知

(39)

(40)

由式(34)、式(39)、式(40)可知

(41)

聯立式(33)、式(41)，可求解得速度脈動的聲、渦模態分量：

(42)

對比式(32)與式(42)可知，渦模態與速度脈動的渦模態分量表達式一致，這與式(25)渦模態的定義及式(33)速度脈動的聲、渦模態分量之間的關系相符。

由式(39)、式(40)、式(42)，可求解得總溫脈動的聲、渦模態分量：

(43)

由式(10)、式(11)可知，在亞聲速風洞等熵流動前提下，密度脈動與靜溫脈動均只存在聲模態分量，且其表達式為

(44)

(45)

根據以上推導結果可以發現：在亞聲速風洞的自由來流中，由于流動可以認為是一維等熵流動，因此密度脈動與靜溫脈動均僅來源于聲模態的貢獻；而速度脈動與總溫脈動來源于聲模態與渦模態兩者的貢獻。

3 試驗結果與分析

3.1 風洞試驗結果

在中國空氣動力研究與發展中心的探針校準風洞中利用熱線測速技術對該風洞亞聲速可壓縮流的流場品質進行了測量，得到了部分馬赫數下質量流量脈動、總溫脈動及其相關量的測量結果[24]，如表1所示。表中，ρmT0為m與T0的相關系數，其定義式為

(46)

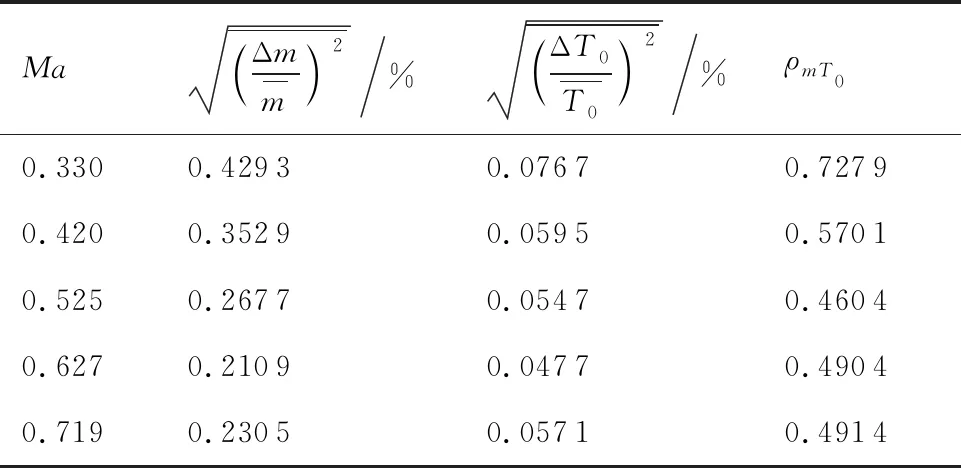
表1 流場品質測量試驗結果[24]

利用以上測量試驗結果，對自由來流擾動模態及流場基本物理量聲、渦模態分量進行求解分析。

3.2 擾動模態求解結果

根據式(30)、式(32)中聲、渦模態的表達式，可利用表1試驗結果對其均方根值進行求解。對于常規亞、跨聲速風洞，由于風洞試驗段及其周邊的收縮段、噴管、擴張段一般均為對稱結構，因此試驗段中的聲擾動模態可視為源于向上游傳播的平面聲波[25]，即平面聲波傳播方向與風洞主流方向的夾角φ=180°。利用表1試驗結果，可計算各個馬赫數下聲、渦模態的均方根值，結果如表2所示，其變化趨勢如圖1所示。

表2 擾動模態計算結果

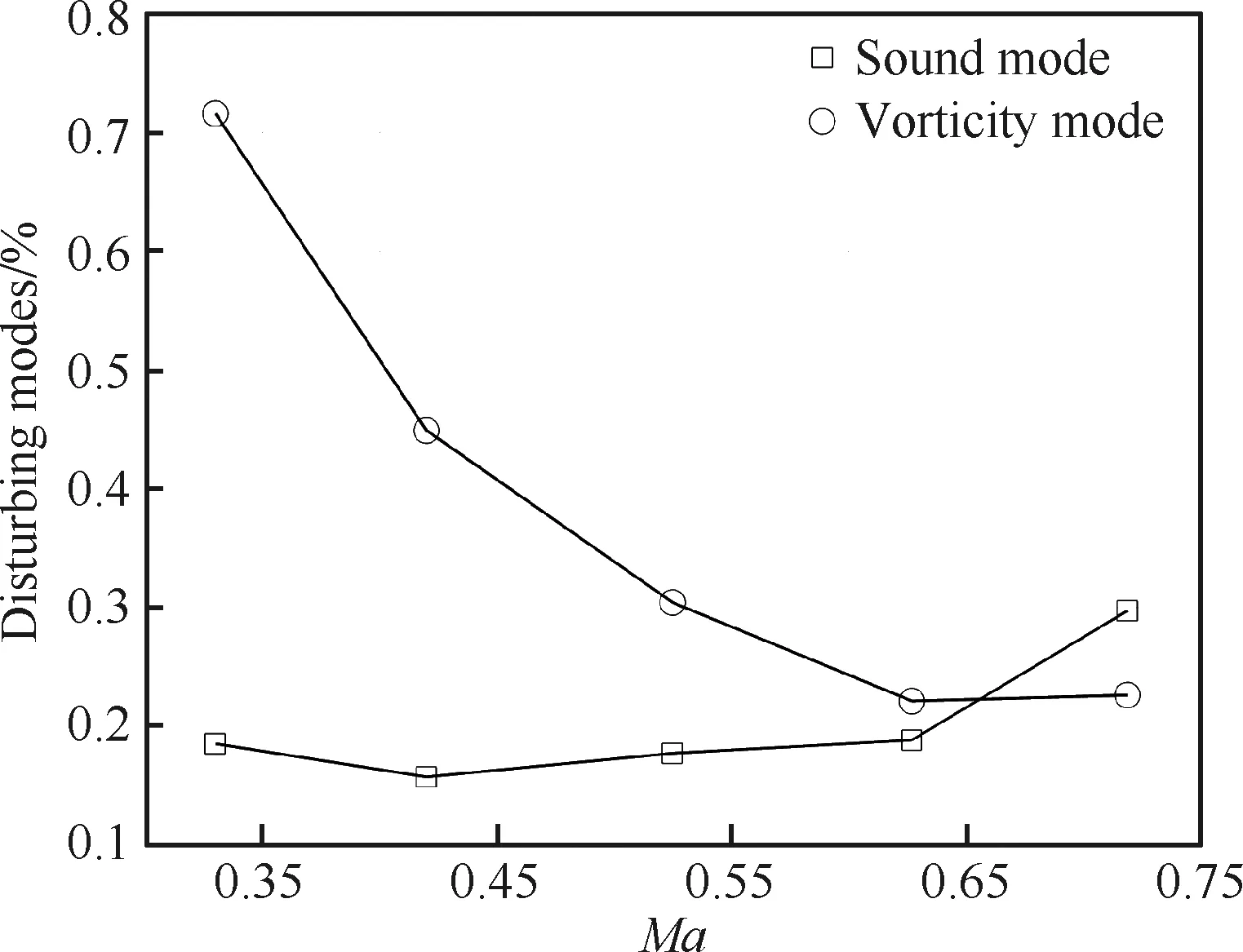
圖1 擾動模態隨馬赫數變化趨勢

由表2及圖1結果可知：隨著馬赫數的提高，聲模態的均方根值總體上呈現出逐漸升高的趨勢，而渦模態的均方根值總體上呈現出逐漸降低的趨勢。

對于聲模態，由于試驗所在的探針校準風洞采用的是直吹射流式布局，隨著試驗馬赫數的提高，熱線探針測量點的靜壓逐漸降低[26]，聲模態的量值總體上呈現出逐漸升高的趨勢。且對于亞聲速可壓縮流，聲模態主要源于湍流摻混噪聲，但隨著馬赫數的提高會逐漸出現嘯音和寬帶激波噪聲[27]，因此，在馬赫數Ma=0.719的情況下，聲模態的量值出現了小幅躍升。而對于低馬赫數Ma=0.330的情況，由于在無引射情況下風洞馬赫數直接由來流總壓控制，馬赫數越低即意味著總壓越低，壓力控制精度相對于總壓的占比就越高，反映在流場上即為馬赫數較低時流動參數脈動會偏大，因此，在馬赫數Ma=0.330的情況下聲模態量值與相鄰馬赫數狀態相比有小幅偏高。

渦模態主要來源于有旋速度脈動，對應于風洞結構其主要產生于閥門的開閉調節、風洞的拐角段、收縮段、擴散段等使得流體速度發生改變的風洞部件，以上部件導致大尺度的旋渦產生，經過蜂窩器及阻尼網等整流裝置后，大尺度的旋渦被“分割”，形成與蜂窩器、阻尼網最小結構單元尺寸相近的小尺度旋渦，最終進入試驗段后，小尺度旋渦誘導的有旋速度脈動導致了渦模態的產生。對于固定的風洞結構，其在試驗段中產生的有旋速度脈動量值基本上不隨馬赫數而改變，因此，隨著馬赫數的提高，渦模態量值呈現出逐漸降低的趨勢。

對比聲、渦模態均方根值結果可知：在馬赫數較低時，自由來流中渦模態占主導，聲模態由于湍流摻混噪聲強度較弱而量值較低；隨著馬赫數進一步提高，由于湍流摻混噪聲強度的提高及嘯音、寬帶激波噪聲的出現，自由來流中聲模態占主導。

3.3 流場基本物理量聲、渦模態分量求解結果

根據2.2節推導結果，利用試驗測量得到的質量流量脈動、總溫脈動及其相關量測量結果，對各個馬赫數下流場基本物理量聲、渦模態分量進行求解，結果如表3所示，其變化趨勢如圖2所示。

表3 流場基本物理量聲、渦模態分量計算結果

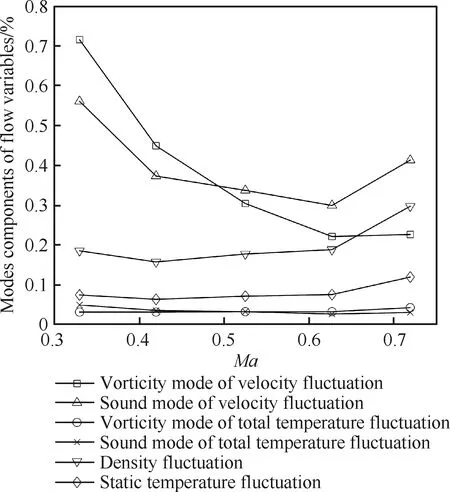
圖2 流場基本物理量聲、渦模態分量隨馬赫數變化趨勢

對比速度脈動聲、渦模態分量結果可知：兩者量值隨馬赫數的變化規律與前文聲、渦模態隨馬赫數的變化規律基本一致，即在馬赫數較低時，渦模態分量占主導，隨著馬赫數的提高，聲模態分量逐漸占主導；且在當前定義體系下，亞聲速一維等熵流動中渦模態與速度脈動渦模態分量雖然定義與表達式均不相同，但兩者的量值相同，這是由于忽略熵模態后其余變量構成方程組的封閉性導致的。由總溫脈動聲、渦模態分量結果可知：兩者的量值相近且相對于其他物理量明顯偏低，說明亞聲速風洞中聲、渦模態對總溫脈動的貢獻相當且均不顯著，即聲、渦模態均不是總溫脈動的主要來源，在超聲速及高超聲速風洞中的熵模態才是總溫脈動的主要來源。由于在亞聲速風洞等熵流動中，密度脈動與靜溫脈動均只存在聲模態分量，其隨馬赫數的變化趨勢與聲模態相同，但密度脈動量值要明顯大于靜溫脈動，說明聲模態對密度脈動的貢獻要大于靜溫脈動，同時說明超聲速及高超聲速風洞中的熵模態是靜溫脈動的重要來源。

4 不確定度分析

為了評估流場品質測量試驗結果的精度，需要對求解結果的不確定度進行評估。由于表1中的流場品質測量試驗結果是通過擬合方法求解得到的，表2與表3中的變量與表1中的變量存在明確的函數關系，因此，可以采用蒙特卡洛模擬方法評估表1中的流場品質測量試驗結果的不確定度[24]，再利用不確定度傳遞公式對表2與表3中求解結果的不確定度進行評估。

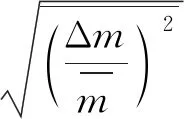
對比表1與表4中的數據可知，流場品質測量試驗結果不確定度要遠小于流場品質結果的量值，說明流場品質測量試驗結果的精度較高。

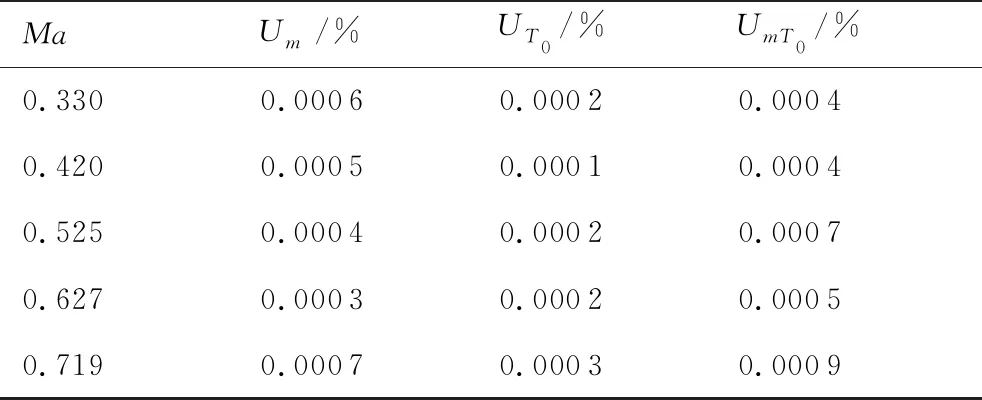
表4 流場品質測量試驗結果不確定度

表5 擾動模態求解結果不確定度

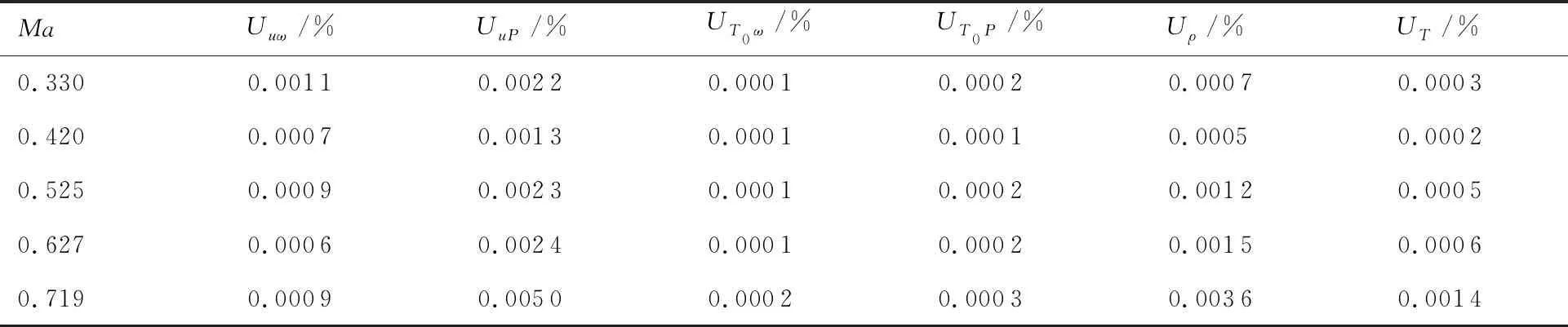
表6 流場基本物理量聲、渦模態分量求解結果不確定度

對比表2與表5中的擾動模態結果及其不確定度、表3與表6中的流場基本物理量聲、渦模態分量結果及其不確定度結果可知，在各個馬赫數下，不確定度最高值占對應變量的1%左右，多數結果中不確定度占對應變量的比例僅為0.1%量級，不確定度的量值遠小于對應變量的量值，說明流場品質測量試驗中擾動模態求解結果及流場基本物理量聲、渦模態分量求解結果具有較高精度。

5 結 論

1) 針對亞聲速風洞可壓縮流體等熵流動前提下的擾動模態進行了分析，從理論上推導了等熵條件下亞聲速風洞中擾動模態的表達式。

2) 通過理論推導建立了擾動模態及流場基本物理量聲、渦模態分量與熱線測速技術測量結果的理論關系。

3) 在馬赫數Ma=0.3～0.7范圍進行了流場品質測量試驗，利用所建立的理論關系對擾動模態及流場基本物理量聲、渦模態分量進行了求解，并對其變化趨勢進行了理論分析。求解結果量值及其變化規律合理，驗證了所建立的理論關系的有效性。

4) 利用蒙特卡洛方法及不確定度傳遞公式對擾動模態及流場基本物理量聲、渦模態分量的不確定度進行了評估，不確定度的量值遠小于其對應變量的量值，驗證了流場品質測量試驗結果的高精度。