帶中介軸承的雙轉(zhuǎn)子系統(tǒng)振動(dòng)耦合作用評(píng)估

王杰，左彥飛,*，江志農(nóng)，馮坤

1. 北京化工大學(xué) 發(fā)動(dòng)機(jī)健康監(jiān)控及網(wǎng)絡(luò)化教育部重點(diǎn)實(shí)驗(yàn)室，北京 100029

2. 北京化工大學(xué) 高端機(jī)械裝備健康監(jiān)控與自愈化北京市重點(diǎn)實(shí)驗(yàn)室，北京 100029

3. 中國(guó)航發(fā)動(dòng)力所—北京化工大學(xué) 航空發(fā)動(dòng)機(jī)振動(dòng)健康監(jiān)控聯(lián)合實(shí)驗(yàn)室，北京 100029

現(xiàn)代燃?xì)鉁u輪發(fā)動(dòng)機(jī)廣泛使用帶中介軸承的雙轉(zhuǎn)子結(jié)構(gòu)設(shè)計(jì)方案。但由于中介軸承的存在，高低壓轉(zhuǎn)子的動(dòng)力特性可能相互影響，導(dǎo)致雙轉(zhuǎn)子系統(tǒng)振動(dòng)變得更為復(fù)雜，給發(fā)動(dòng)機(jī)結(jié)構(gòu)系統(tǒng)設(shè)計(jì)和振動(dòng)故障診斷帶來(lái)困難和挑戰(zhàn)。

為研究帶中介軸承的雙轉(zhuǎn)子系統(tǒng)動(dòng)力特性，1980年，Hibner[1]用傳遞矩陣法計(jì)算分析了具有黏性阻尼雙轉(zhuǎn)子系統(tǒng)的臨界轉(zhuǎn)速及不平衡響應(yīng)。20世紀(jì)90年代，Gupta等[2-3]研究并分析了輪盤的轉(zhuǎn)動(dòng)慣量和陀螺效應(yīng)對(duì)雙轉(zhuǎn)子動(dòng)力特性的影響。此后，Guskov[4]、羅貴火[5-7]等、采用傳遞矩陣法研究并驗(yàn)證了雙轉(zhuǎn)子系統(tǒng)的典型振動(dòng)特性以及支承剛度、陀螺效應(yīng)對(duì)雙轉(zhuǎn)子振動(dòng)特性的影響。洪杰[8-9]、張大義[10-11]和左彥飛[12-14]等針對(duì)發(fā)動(dòng)機(jī)的雙轉(zhuǎn)子系統(tǒng)，主要使用有限元模型研究了臨界轉(zhuǎn)速、穩(wěn)態(tài)不平衡響應(yīng)的計(jì)算分析方法，對(duì)典型發(fā)動(dòng)機(jī)的雙轉(zhuǎn)子系統(tǒng)動(dòng)力特性進(jìn)行了分析，得到了系統(tǒng)響應(yīng)特征，并研究了支承非對(duì)稱等因素的影響。在雙轉(zhuǎn)子系統(tǒng)線性動(dòng)力特性研究的基礎(chǔ)上，近年來(lái)學(xué)者對(duì)非線性因素影響下的雙轉(zhuǎn)子系統(tǒng)響應(yīng)也做了較為深入研究[15-20]。不過(guò)，現(xiàn)有的研究主要集中于雙轉(zhuǎn)子-中介軸承系統(tǒng)建模，臨界轉(zhuǎn)速、不平衡響應(yīng)的計(jì)算分析，以及考慮中介軸承非線性的動(dòng)力學(xué)特性分析等。主要通過(guò)計(jì)算出的響應(yīng)結(jié)果、軸心軌跡或試驗(yàn)的現(xiàn)象，研究雙轉(zhuǎn)子系統(tǒng)振動(dòng)特征。雙轉(zhuǎn)子系統(tǒng)因中介軸承而存在振動(dòng)耦合作用的機(jī)理以及如何進(jìn)行評(píng)估耦合的強(qiáng)弱等問(wèn)題，在雙轉(zhuǎn)子系統(tǒng)設(shè)計(jì)或振動(dòng)故障分析中具有重要意義，還需要深入研究。

為此，通過(guò)單轉(zhuǎn)子和耦合雙轉(zhuǎn)子系統(tǒng)的振型相似性變化、臨界轉(zhuǎn)速變化、中介軸承受力變化、工作轉(zhuǎn)速內(nèi)系統(tǒng)應(yīng)變能分布變化分析等，提出雙轉(zhuǎn)子系統(tǒng)振動(dòng)耦合作用機(jī)理及影響評(píng)估方法，以某典型帶有中介軸承的發(fā)動(dòng)機(jī)雙轉(zhuǎn)子系統(tǒng)為對(duì)象，分析了該雙轉(zhuǎn)子系統(tǒng)通過(guò)中介軸承的耦合作用，為類似的發(fā)動(dòng)機(jī)轉(zhuǎn)子系統(tǒng)動(dòng)力設(shè)計(jì)及故障診斷提供參考。

1 耦合作用評(píng)估方法

1.1 轉(zhuǎn)子系統(tǒng)動(dòng)力學(xué)方程

基于有限元建模的單轉(zhuǎn)子系統(tǒng)動(dòng)力學(xué)方程可表示為

(1)

式中：Mi、Ci、Gi、Ki、Ωi、fi分別為單轉(zhuǎn)子系統(tǒng)的質(zhì)量矩陣、阻尼矩陣、陀螺矩陣、剛度矩陣、轉(zhuǎn)速、激勵(lì)向量；ui為單轉(zhuǎn)子系統(tǒng)振動(dòng)位移向量；t為時(shí)間；j為虛數(shù)。

帶有中介軸承的雙轉(zhuǎn)子系統(tǒng)的動(dòng)力學(xué)方程可表示為[12]

(2)

式中：M、C、Kd分別為雙轉(zhuǎn)子系統(tǒng)質(zhì)量矩陣、阻尼矩陣、剛度矩陣；Ω1、G1、K1、f1和Ω2、G2、K2、f2分別為低壓轉(zhuǎn)子(轉(zhuǎn)子1)和高壓轉(zhuǎn)子(轉(zhuǎn)子2)的轉(zhuǎn)速、旋轉(zhuǎn)產(chǎn)生的陀螺效應(yīng)矩陣、轉(zhuǎn)速相關(guān)的剛度矩陣、激勵(lì)向量；u為雙轉(zhuǎn)子系統(tǒng)振動(dòng)位移向量。

對(duì)于連接雙轉(zhuǎn)子的中介軸承，若忽略其質(zhì)量、阻尼、非線性因素，剛度矩陣用kb表示，設(shè)中介軸承與低壓轉(zhuǎn)子、高壓轉(zhuǎn)子相連接節(jié)點(diǎn)編號(hào)分別為l、h，則中介軸承與低、高壓轉(zhuǎn)子耦合的力學(xué)方程可表示為[13]

(3)

比較式(1)～式(3)可以看出，相對(duì)于單轉(zhuǎn)子系統(tǒng)，中介軸承的連接作用的影響主要有兩方面：一是系統(tǒng)剛度的明顯變化，會(huì)使系統(tǒng)的固有特性發(fā)生變化；二是傳遞復(fù)雜不平衡激勵(lì)到另一個(gè)轉(zhuǎn)子，會(huì)使得系統(tǒng)的響應(yīng)特性發(fā)生變化。因此，對(duì)中介軸承耦合作用機(jī)理及影響的評(píng)估將主要從轉(zhuǎn)子的振型、臨界轉(zhuǎn)速等固有特性以及不平衡響應(yīng)特性兩個(gè)方面開展。

1.2 中介軸承耦合作用對(duì)振型與臨界轉(zhuǎn)速的影響

利用復(fù)模態(tài)求解方法，可由式(1)得到單轉(zhuǎn)子系統(tǒng)的臨界轉(zhuǎn)速對(duì)應(yīng)的模態(tài)振型矢量Ψs(Ωcn)，其中Ωcn表示單個(gè)轉(zhuǎn)子的第n階臨界轉(zhuǎn)速。

而對(duì)于特定的雙轉(zhuǎn)子系統(tǒng)，兩個(gè)轉(zhuǎn)子的轉(zhuǎn)速關(guān)系往往是確定的。假設(shè)兩個(gè)轉(zhuǎn)子的轉(zhuǎn)速關(guān)系符合：

Ω2=f(Ω1)

(4)

并利用文獻(xiàn)[10]所述的雙轉(zhuǎn)子系統(tǒng)臨界復(fù)模態(tài)求解方法，可由式(2)得到被耦合轉(zhuǎn)子激勵(lì)的臨界轉(zhuǎn)速對(duì)應(yīng)的模態(tài)振型矢量Ψd(Ωcm)，其中Ωcm表示雙轉(zhuǎn)子系統(tǒng)的第m階臨界轉(zhuǎn)速。

1.2.1 振型及臨界轉(zhuǎn)速變化評(píng)估

為研究中介軸承及另一個(gè)轉(zhuǎn)子的存在對(duì)原單一轉(zhuǎn)子系統(tǒng)振型(頻率)產(chǎn)生的影響，利用振型相似性指標(biāo)-振型置信因子(量符號(hào)記為Cma)來(lái)定量評(píng)估振型的受影響程度。理論上轉(zhuǎn)子振型受轉(zhuǎn)速影響，模態(tài)置信因子是兩個(gè)轉(zhuǎn)子轉(zhuǎn)速的函數(shù)。不過(guò)，由于工程中比較關(guān)注臨界轉(zhuǎn)速對(duì)應(yīng)的轉(zhuǎn)子振型，所以提出臨界轉(zhuǎn)速對(duì)應(yīng)的模態(tài)振型置信因子，其表達(dá)式為

(5)

式中：Cmamn為同一轉(zhuǎn)子耦合前的第n階臨界轉(zhuǎn)速與耦合后的第m階臨界轉(zhuǎn)速的振型置信因子；n表示單個(gè)轉(zhuǎn)子(低壓或高壓轉(zhuǎn)子)在轉(zhuǎn)速范圍內(nèi)臨界轉(zhuǎn)速的階次；m表示該轉(zhuǎn)子激勵(lì)的雙轉(zhuǎn)子在轉(zhuǎn)速范圍內(nèi)臨界轉(zhuǎn)速的階次。

通過(guò)計(jì)算振型置信因子，得到不同階模態(tài)振型的相似性。當(dāng)Cmamn為1.00時(shí)，兩個(gè)振型完全相同，越接近于1.00相似性越大，Cmamn最小為0[21]。通過(guò)Cmamn的大小，并結(jié)合對(duì)應(yīng)的振型，評(píng)估單轉(zhuǎn)子耦合前后在臨界轉(zhuǎn)速位置的振型受影響程度。

進(jìn)一步研究轉(zhuǎn)子耦合前后Cmamn較大的兩組振型Ψs(Ωcp)、Ψd(Ωcq)對(duì)應(yīng)的臨界轉(zhuǎn)速的相對(duì)變化率，可以表示為

(6)

1.2.2 振型應(yīng)變能變化評(píng)估

在發(fā)動(dòng)機(jī)轉(zhuǎn)子系統(tǒng)設(shè)計(jì)中，可根據(jù)應(yīng)變能分布準(zhǔn)確判定系統(tǒng)振型中轉(zhuǎn)子與機(jī)匣振動(dòng)主次，如果轉(zhuǎn)子部件的彎曲應(yīng)變能過(guò)高，則要通過(guò)設(shè)置阻尼器、柔性轉(zhuǎn)子高速動(dòng)平衡等措施調(diào)整應(yīng)變能分布，因而具有重要作用。在雙轉(zhuǎn)子-支承系統(tǒng)中，由于轉(zhuǎn)子通過(guò)中介軸承與另一轉(zhuǎn)子耦合，應(yīng)變能的分布變化在系統(tǒng)設(shè)計(jì)與故障診斷應(yīng)重點(diǎn)關(guān)注。為了定量分析單一轉(zhuǎn)子系統(tǒng)耦合前后臨界轉(zhuǎn)速對(duì)應(yīng)振型的應(yīng)變能變化情況，提出模態(tài)應(yīng)變能占比變化量指標(biāo)。

若Ee1、Er1、Ep1、Ea1和Ee2、Er2、Ep2、Ea2分別表示單轉(zhuǎn)子耦合前后在臨界轉(zhuǎn)速時(shí)的單元應(yīng)變能、轉(zhuǎn)子應(yīng)變能、單個(gè)支承應(yīng)變能、所有支承單元應(yīng)變能。則單元、轉(zhuǎn)子、單個(gè)支承、所有支承的相似模態(tài)振型在耦合前后的模態(tài)應(yīng)變能占比變化量可表示為

(7)

式中：*可表示e、r、p、a。

1.3 中介軸承耦合作用對(duì)不平衡響應(yīng)的影響

由于轉(zhuǎn)子系統(tǒng)的固有特性受轉(zhuǎn)速的影響，且在設(shè)計(jì)或故障診斷時(shí)常常需要考慮在0～110%工作轉(zhuǎn)速范圍內(nèi)響應(yīng)特性。求解得到式(2)所述的雙轉(zhuǎn)子動(dòng)力學(xué)方程中低、高壓轉(zhuǎn)子分別激勵(lì)下轉(zhuǎn)子系統(tǒng)的響應(yīng)：

(8)

式中：

由于中介軸承為連接兩個(gè)轉(zhuǎn)子的關(guān)鍵承力部件，雙轉(zhuǎn)子不平衡振動(dòng)相互耦合作用主要由中介軸承傳遞，全轉(zhuǎn)速范圍內(nèi)中介軸承受力變化可以從相互作用力的角度表征雙轉(zhuǎn)子間的耦合程度，同時(shí)可為中介軸承設(shè)計(jì)及故障診斷等提供參考，中介軸承受力表示為

fb=Δu·kb

(9)

在此基礎(chǔ)上，進(jìn)一步評(píng)估在中介軸承耦合作用下，從單轉(zhuǎn)子系統(tǒng)到雙轉(zhuǎn)子系統(tǒng)，全轉(zhuǎn)速范圍內(nèi)的不平衡振動(dòng)能量分布變化情況。分別計(jì)算特定不平衡激勵(lì)下單轉(zhuǎn)子及雙轉(zhuǎn)子系統(tǒng)在每個(gè)轉(zhuǎn)速下的單元應(yīng)變能、轉(zhuǎn)子應(yīng)變能、支承系統(tǒng)應(yīng)變能，則利用式(7)可以計(jì)算得到轉(zhuǎn)子系統(tǒng)應(yīng)變能占比變化量，進(jìn)而可以評(píng)估整個(gè)轉(zhuǎn)速范圍內(nèi)轉(zhuǎn)子受耦合的影響程度。

2 典型帶中介軸承的雙轉(zhuǎn)子系統(tǒng)耦合動(dòng)力特性分析

以文獻(xiàn)[14]所述的同向旋轉(zhuǎn)雙轉(zhuǎn)子系統(tǒng)為對(duì)象，結(jié)合所提評(píng)估方法，研究中介軸承的耦合作用對(duì)雙轉(zhuǎn)子動(dòng)力特性的影響規(guī)律。

2.1 典型發(fā)動(dòng)機(jī)雙轉(zhuǎn)子支承系統(tǒng)

如圖1所示，該雙轉(zhuǎn)子系統(tǒng)共有6個(gè)支點(diǎn)(軸承)位置，其中1號(hào)、2號(hào)、3號(hào)與6號(hào)支點(diǎn)為低壓轉(zhuǎn)子支點(diǎn)，4號(hào)支點(diǎn)位置為高壓轉(zhuǎn)子支點(diǎn)，5號(hào)支點(diǎn)為中介支點(diǎn)，低壓壓氣機(jī)與低壓渦輪通過(guò)低壓渦輪軸連接組成低壓轉(zhuǎn)子。轉(zhuǎn)子的軸向?yàn)閄方向，與X方向垂直的平面內(nèi)相互垂直的兩個(gè)方向分別為Y、Z方向。雙轉(zhuǎn)子的主要部件參數(shù)見表1[14]， 雙轉(zhuǎn)子系統(tǒng)的對(duì)稱支承經(jīng)驗(yàn)剛度見表2，低、高壓轉(zhuǎn)子分別計(jì)算時(shí)的經(jīng)驗(yàn)剛度見表3、表4，其中單轉(zhuǎn)子計(jì)算時(shí)高壓轉(zhuǎn)子5號(hào)支點(diǎn)的剛度通過(guò)低壓轉(zhuǎn)子5號(hào)支點(diǎn)位置的靜剛度計(jì)算分析得到。參考該發(fā)動(dòng)機(jī)雙轉(zhuǎn)子的實(shí)際工作轉(zhuǎn)速變化規(guī)律，簡(jiǎn)化為文獻(xiàn)[14]中圖2所示的轉(zhuǎn)速關(guān)系進(jìn)行相關(guān)的動(dòng)力特性分析。

圖1 典型雙轉(zhuǎn)子系統(tǒng)有限元模型

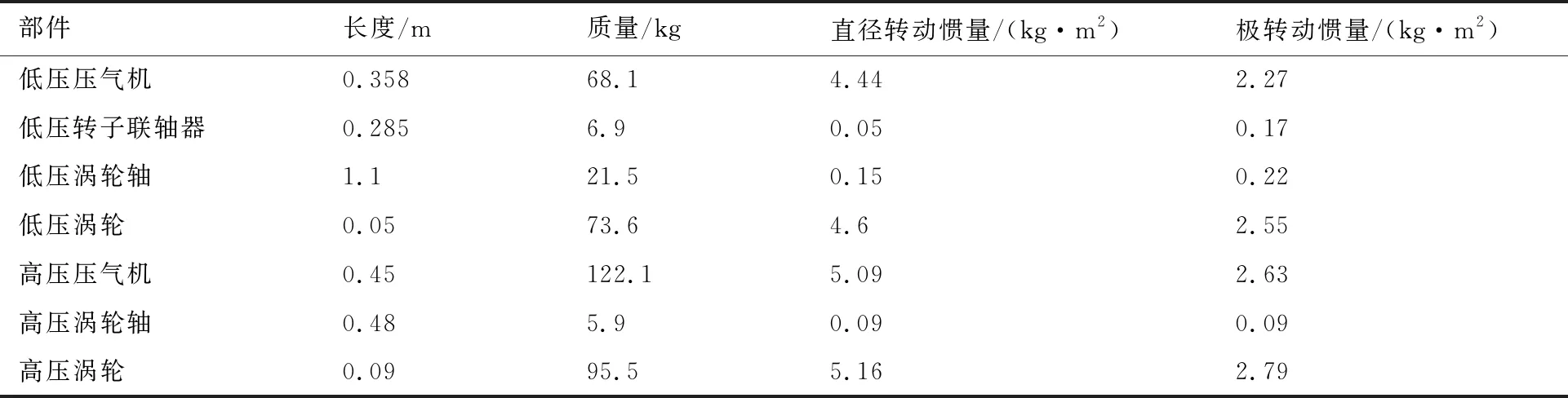
表1 雙轉(zhuǎn)子主要部件及參數(shù)[14]

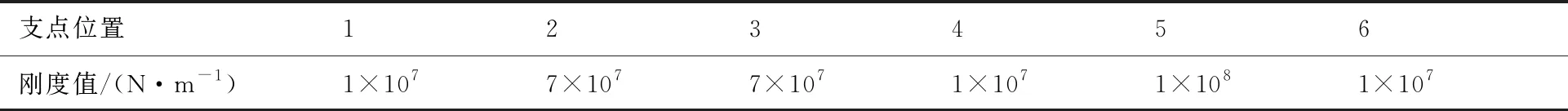
表2 雙轉(zhuǎn)子系統(tǒng)的對(duì)稱支承經(jīng)驗(yàn)剛度

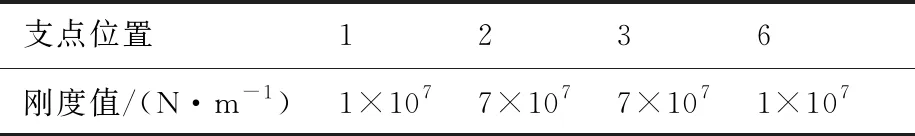
表3 低壓轉(zhuǎn)子系統(tǒng)的對(duì)稱支承經(jīng)驗(yàn)剛度

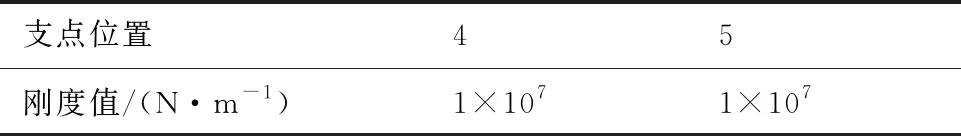
表4 高壓轉(zhuǎn)子系統(tǒng)的對(duì)稱支承經(jīng)驗(yàn)剛度

2.2 耦合作用對(duì)振型與臨界轉(zhuǎn)速的影響

根據(jù)1.2.1節(jié)所述的評(píng)估方法，研究并評(píng)估中介軸承耦合作用對(duì)振型與臨界轉(zhuǎn)速的影響。

通過(guò)分別對(duì)低壓轉(zhuǎn)子、高壓轉(zhuǎn)子以及雙轉(zhuǎn)子進(jìn)行模態(tài)計(jì)算，并利用式(5)計(jì)算得到的單獨(dú)低、高壓轉(zhuǎn)子與雙轉(zhuǎn)子耦合時(shí)的低、高壓轉(zhuǎn)子的振型置信因子分別如表5、表6所示，F(xiàn)表示正進(jìn)動(dòng)，B表示反進(jìn)動(dòng)，例如，1stF表示第1階正進(jìn)動(dòng)臨界轉(zhuǎn)速，2ndB表示第2階反進(jìn)動(dòng)臨界轉(zhuǎn)速。表中：加粗且?guī)聞澗€的數(shù)字表示單獨(dú)低壓轉(zhuǎn)子或高壓轉(zhuǎn)子與耦合雙轉(zhuǎn)子系統(tǒng)明顯相似的振型置信因子；L、H分別表示單獨(dú)低壓、高壓轉(zhuǎn)子臨界轉(zhuǎn)速階數(shù)，L-D、H-D分別表示低壓、高壓轉(zhuǎn)子激勵(lì)的雙轉(zhuǎn)子臨界轉(zhuǎn)速階數(shù)。

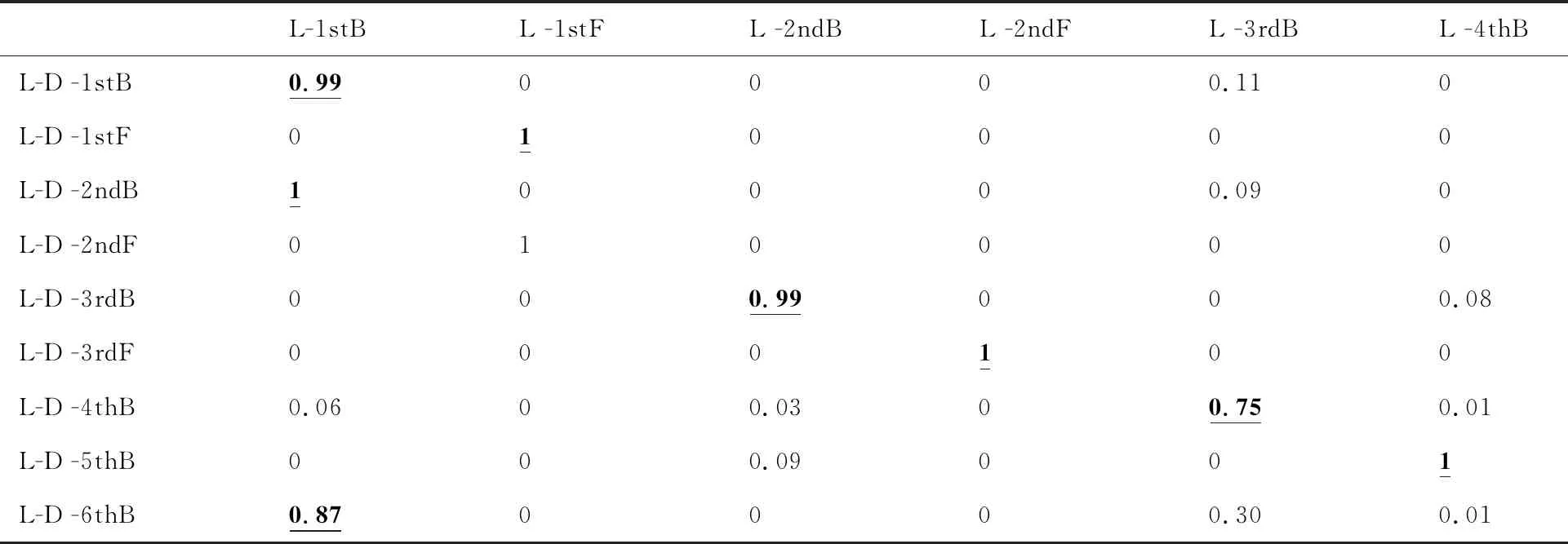
表5 低壓轉(zhuǎn)子激勵(lì)與臨界轉(zhuǎn)速對(duì)應(yīng)模態(tài)振型置信因子

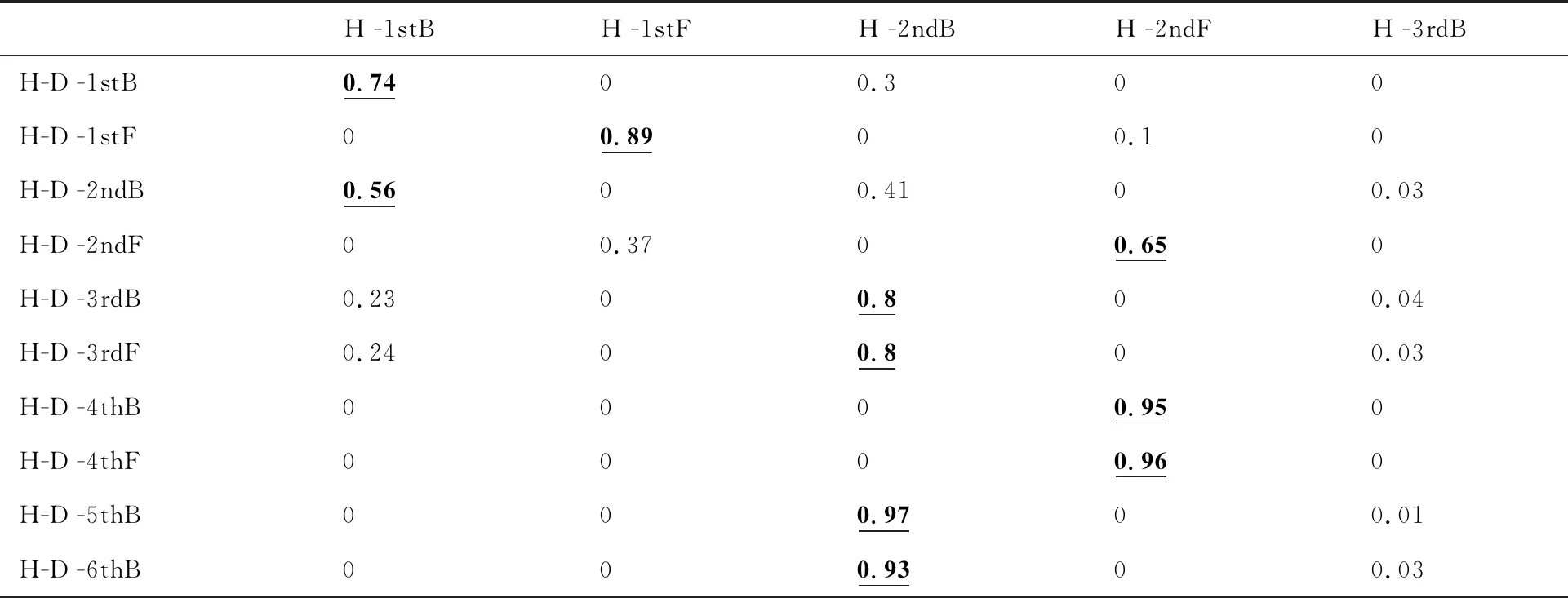
表6 高壓轉(zhuǎn)子激勵(lì)與臨界轉(zhuǎn)速對(duì)應(yīng)模態(tài)振型置信因子

由表5、表6可以看出，單轉(zhuǎn)子的某些模態(tài)振型會(huì)在雙轉(zhuǎn)子高階模態(tài)振型中出現(xiàn)，且為一對(duì)一的對(duì)應(yīng)關(guān)系。例如單獨(dú)低壓轉(zhuǎn)子的2ndB、2ndF和4thB振型分別與雙轉(zhuǎn)子中低壓轉(zhuǎn)子激勵(lì)的3rdB、3rdF和5thB階模態(tài)置信因子均在0.99以上，通過(guò)圖2所示振型圖，可以看出這幾階振型均以低壓壓氣機(jī)的橫向振動(dòng)為主，低壓渦輪和高壓轉(zhuǎn)子的振動(dòng)較小，故振型相似度較高。進(jìn)一步通過(guò)式(6)計(jì)算得到表7(其中L-D-C表示低壓轉(zhuǎn)子激勵(lì)臨界轉(zhuǎn)速，L-C表示低壓轉(zhuǎn)子臨界轉(zhuǎn)速，下文相同)，可以看出與振型對(duì)應(yīng)的臨界轉(zhuǎn)速相對(duì)變化率較小。

圖2 雙轉(zhuǎn)子中低壓轉(zhuǎn)子激勵(lì)的3rdB、3rdF、5thB和低壓轉(zhuǎn)子對(duì)應(yīng)振型比較

表7 雙轉(zhuǎn)子中低壓轉(zhuǎn)子激勵(lì)的3rdB、3rdF、5thB和低壓轉(zhuǎn)子對(duì)應(yīng)臨界轉(zhuǎn)速比較

此外，單轉(zhuǎn)子的特定模態(tài)振型可能在雙轉(zhuǎn)子模態(tài)振型中反復(fù)出現(xiàn)。例如單獨(dú)低壓轉(zhuǎn)子1 stF與雙轉(zhuǎn)子中低壓轉(zhuǎn)子激勵(lì)的1 stF與2ndF模態(tài)振型置信因子均為1，可以看出其振型(圖3)也明顯高度相似，均以低壓渦輪和高壓轉(zhuǎn)子的俯仰振動(dòng)為主，區(qū)別之處在于高壓轉(zhuǎn)子振型不同。但由表8可以看出與振型對(duì)應(yīng)的臨界轉(zhuǎn)速相對(duì)變化率可能較大。

表8 雙轉(zhuǎn)子中低壓轉(zhuǎn)子激勵(lì)的1stF、2ndF和低壓轉(zhuǎn)子對(duì)應(yīng)臨界轉(zhuǎn)速比較

特殊的，由表6可以看出，雙轉(zhuǎn)子中高壓轉(zhuǎn)子的某些模態(tài)振型是由單獨(dú)高壓轉(zhuǎn)子的多階不同占比的模態(tài)振型組成。例如雙轉(zhuǎn)子的1stB對(duì)應(yīng)的單轉(zhuǎn)子的1stB與2ndB的置信因子和約為1；雙轉(zhuǎn)子的2ndB對(duì)應(yīng)的單轉(zhuǎn)子的1stB、2ndB和3rdB的置信因子和約為1；雙轉(zhuǎn)子的2ndF對(duì)應(yīng)的單轉(zhuǎn)子的1stF和2ndF的振型因子和約為1，其中單獨(dú)高壓轉(zhuǎn)子的各階振型分別如圖4(d)～4(h)所示。說(shuō)明在這些臨界轉(zhuǎn)速位置，雙轉(zhuǎn)子系統(tǒng)的振型與單獨(dú)轉(zhuǎn)子系統(tǒng)相比發(fā)生明顯的變化，此時(shí)，中

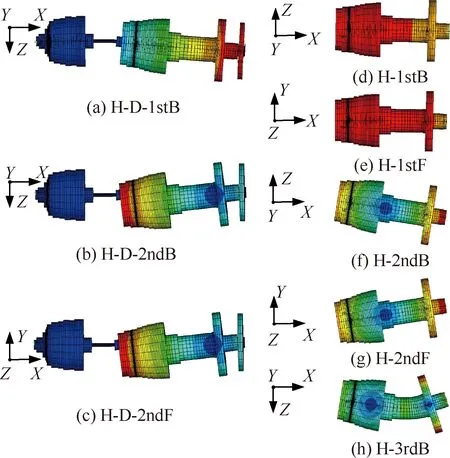
圖4 雙轉(zhuǎn)子中高壓轉(zhuǎn)子激勵(lì)的1stF、2ndB、2ndF和高壓轉(zhuǎn)子對(duì)應(yīng)振型比較

介軸承的連接作用使得高壓轉(zhuǎn)子的支承特性發(fā)生顯著變化，進(jìn)而引起高壓轉(zhuǎn)子的兩階或多階振型發(fā)生耦合形成新的振型。由對(duì)應(yīng)臨界轉(zhuǎn)速的變化關(guān)系(表9，其中H-D-C表示高壓轉(zhuǎn)子激勵(lì)臨界轉(zhuǎn)速，H-C表示高壓轉(zhuǎn)子臨界轉(zhuǎn)速)可以看出，振型相似性較高的振型對(duì)應(yīng)臨界轉(zhuǎn)速變化可能較小，振型相似性較低的振型對(duì)應(yīng)臨界轉(zhuǎn)速變化可能較大。

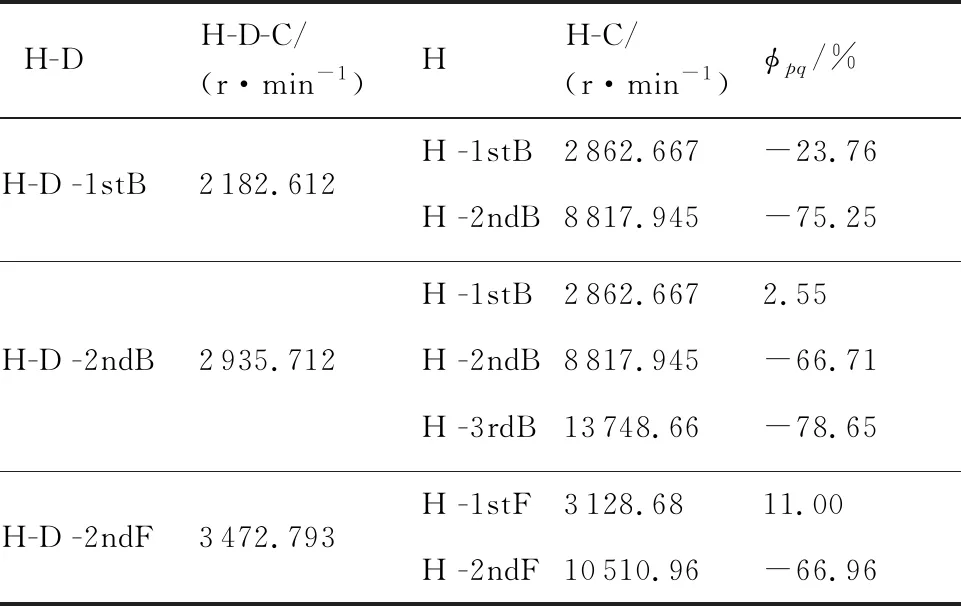
表9 雙轉(zhuǎn)子中高壓轉(zhuǎn)子激勵(lì)的1stF、2ndB、2ndF和高壓轉(zhuǎn)子對(duì)應(yīng)臨界轉(zhuǎn)速比較

在上述3種情況的振型相似性及臨界轉(zhuǎn)速變化分析的基礎(chǔ)上，利用1.2.2節(jié)所述的振型應(yīng)變能變化評(píng)估方法，進(jìn)一步分析臨界轉(zhuǎn)速模態(tài)應(yīng)變能的變化情況。

1) 對(duì)于單轉(zhuǎn)子與雙轉(zhuǎn)子呈一一的對(duì)應(yīng)振型且相似性較高的情況：雙轉(zhuǎn)子中低壓轉(zhuǎn)子激勵(lì)的3rdB、3rdF和5thB振型對(duì)應(yīng)的模態(tài)應(yīng)變能如表10所示，可以看出，各部分應(yīng)變能占比變化量最大不超過(guò)4%，此種情況下各階臨界轉(zhuǎn)速對(duì)應(yīng)轉(zhuǎn)子、支點(diǎn)的應(yīng)變能占比變化量均較小，結(jié)合振型分析可知這些臨界轉(zhuǎn)速均以低壓壓氣機(jī)振動(dòng)為主，中介軸承耦合作用甚微。

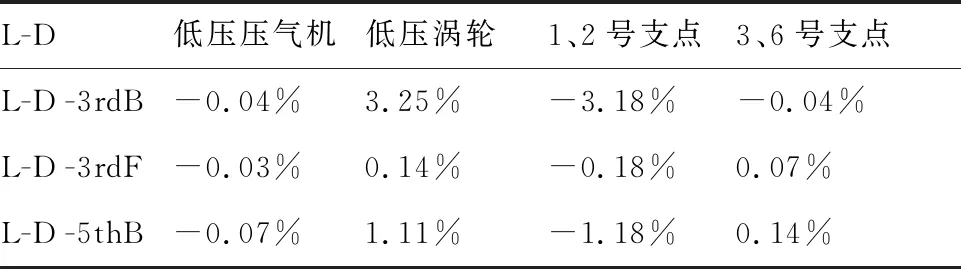
表10 低壓轉(zhuǎn)子激勵(lì)的3rdB、3rdF和5thB臨界轉(zhuǎn)速對(duì)應(yīng)的模態(tài)振型應(yīng)變能占比變化量

2) 對(duì)于單轉(zhuǎn)子的某階模態(tài)振型在雙轉(zhuǎn)子模態(tài)振型中反復(fù)出現(xiàn)的情況：?jiǎn)为?dú)低壓轉(zhuǎn)子1stF與雙轉(zhuǎn)子中低壓轉(zhuǎn)子激勵(lì)的1stF與2ndF振型對(duì)應(yīng)的模態(tài)應(yīng)變能如表11所示，可以看出，各部分應(yīng)變能占比變化量最大不超過(guò)2%，此種情況下轉(zhuǎn)子、支點(diǎn)對(duì)應(yīng)的模態(tài)應(yīng)變能占比也均較小，結(jié)合振型分析可知，這種情況下，高壓轉(zhuǎn)子的振型及其變化對(duì)低壓轉(zhuǎn)子影響很小。

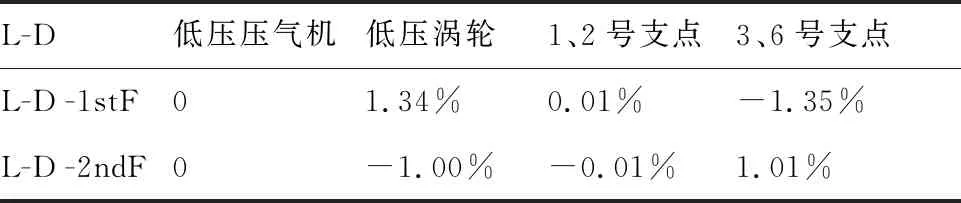
表11 低壓轉(zhuǎn)子激勵(lì)的1stF、2ndF臨界轉(zhuǎn)速對(duì)應(yīng)模態(tài)振型應(yīng)變能占比變化量

3) 對(duì)于雙轉(zhuǎn)子中高壓轉(zhuǎn)子的單階模態(tài)振型是由單獨(dú)高壓轉(zhuǎn)子的多階不同占比的模態(tài)振型組

成的情況，雙轉(zhuǎn)子中高壓轉(zhuǎn)子激勵(lì)的1stB、2ndB和2ndF振型與單獨(dú)高壓轉(zhuǎn)子對(duì)應(yīng)振型的模態(tài)應(yīng)變能占比變化量如表12所示。可以看出，振型置信因子較小的應(yīng)變能占比變化量較大，如雙轉(zhuǎn)子中高壓轉(zhuǎn)子激勵(lì)的2ndB與單獨(dú)高壓轉(zhuǎn)子3rdB的置信因子為0.03，高壓轉(zhuǎn)子應(yīng)變能占比變化量達(dá)到了-98.26%；但是對(duì)于模態(tài)振型置信因子越大對(duì)應(yīng)的應(yīng)變能占比變化量卻不一定小。

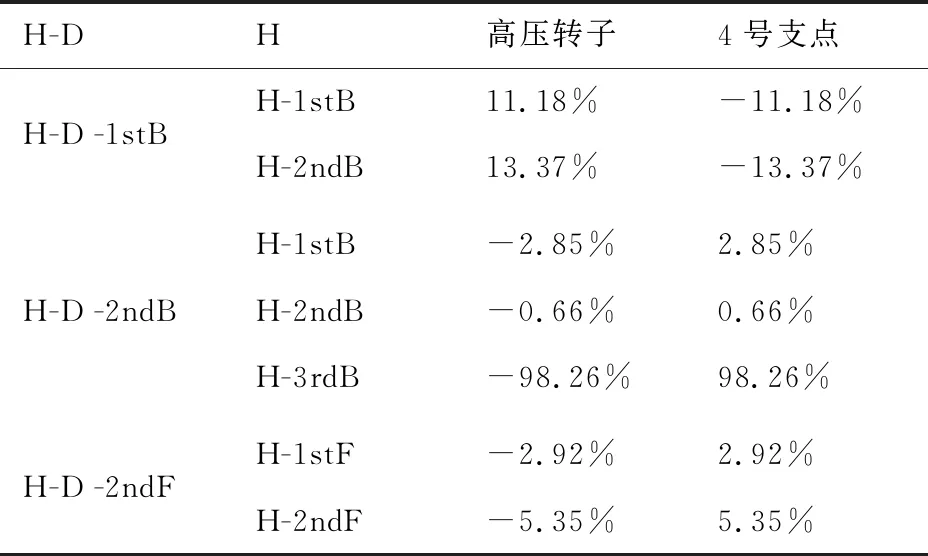
表12 高壓轉(zhuǎn)子激勵(lì)的1stB、2ndB和2ndF臨界轉(zhuǎn)速對(duì)應(yīng)模態(tài)振型應(yīng)變能占比變化量

2.3 耦合作用對(duì)穩(wěn)態(tài)不平衡響應(yīng)的影響

利用1.3節(jié)的評(píng)估方法，研究中介軸承耦合作用對(duì)不平衡響應(yīng)的影響。

當(dāng)?shù)蛪簻u輪葉盤、高壓渦輪葉盤上分別施加2 g·m允許不平衡量時(shí)，求解得到的雙轉(zhuǎn)子系統(tǒng)各支點(diǎn)的響應(yīng)分別如圖5、圖6所示。轉(zhuǎn)子各支點(diǎn)臨界轉(zhuǎn)速位置響應(yīng)的相對(duì)大小與振型相關(guān)及激勵(lì)位置相關(guān)，這與文獻(xiàn)[12]的結(jié)論一致。

進(jìn)一步分析中介軸承彈簧單元在低壓轉(zhuǎn)子、高壓轉(zhuǎn)子受耦合時(shí)力的傳遞關(guān)系，分別繪制低壓、高壓轉(zhuǎn)子激勵(lì)時(shí)5號(hào)支點(diǎn)節(jié)點(diǎn)力隨轉(zhuǎn)速的變化規(guī)律如圖7、圖8所示，結(jié)合圖5、圖6可知，中介軸承節(jié)點(diǎn)力與位移響應(yīng)曲線在轉(zhuǎn)速范圍內(nèi)的變化一致，在臨界轉(zhuǎn)速位置同時(shí)到達(dá)峰值，且高、低壓轉(zhuǎn)子5號(hào)支點(diǎn)節(jié)點(diǎn)力隨轉(zhuǎn)速變化曲線相同。

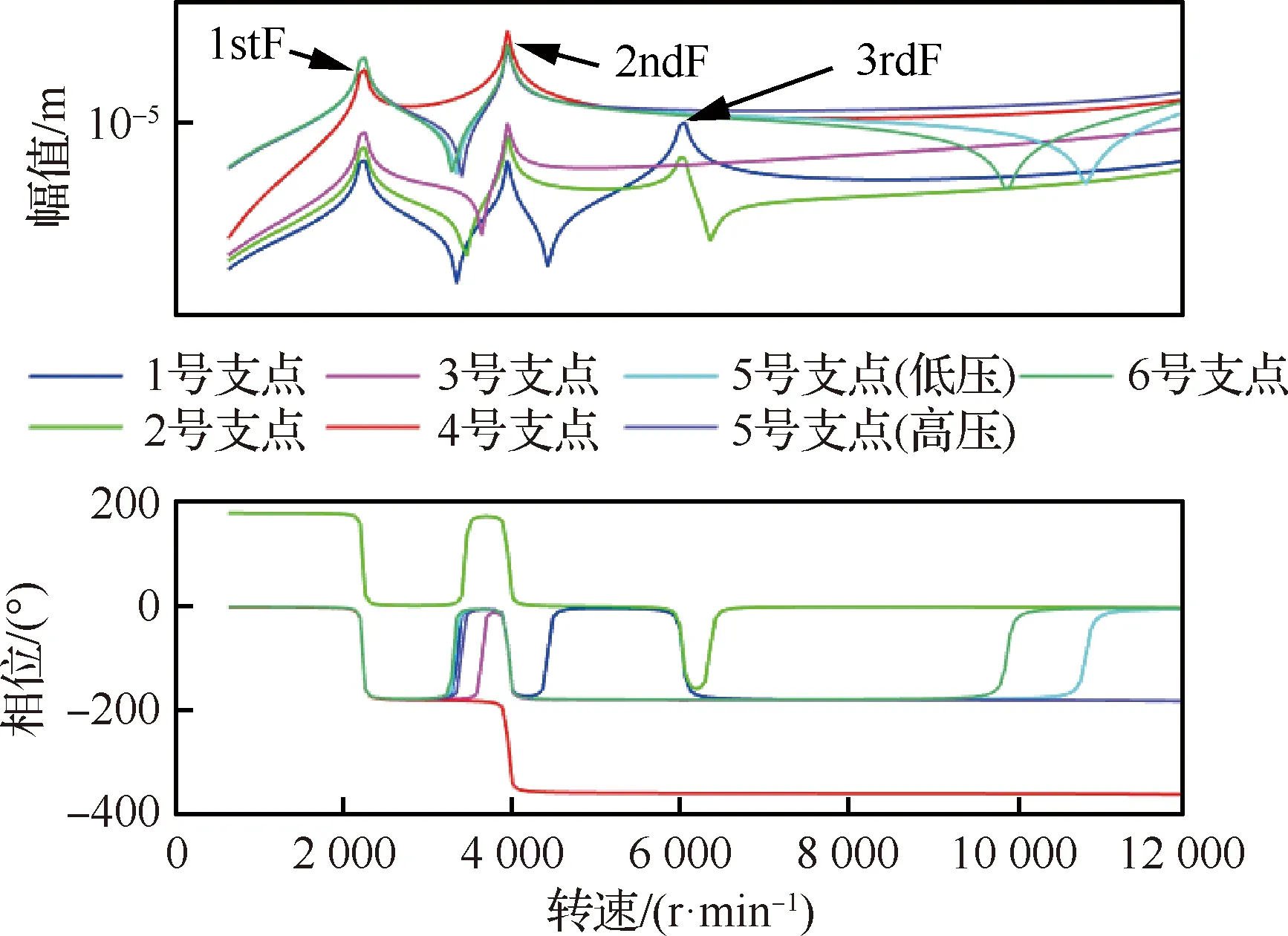
圖5 低壓轉(zhuǎn)子激勵(lì)時(shí)雙轉(zhuǎn)子各支點(diǎn)的響應(yīng)

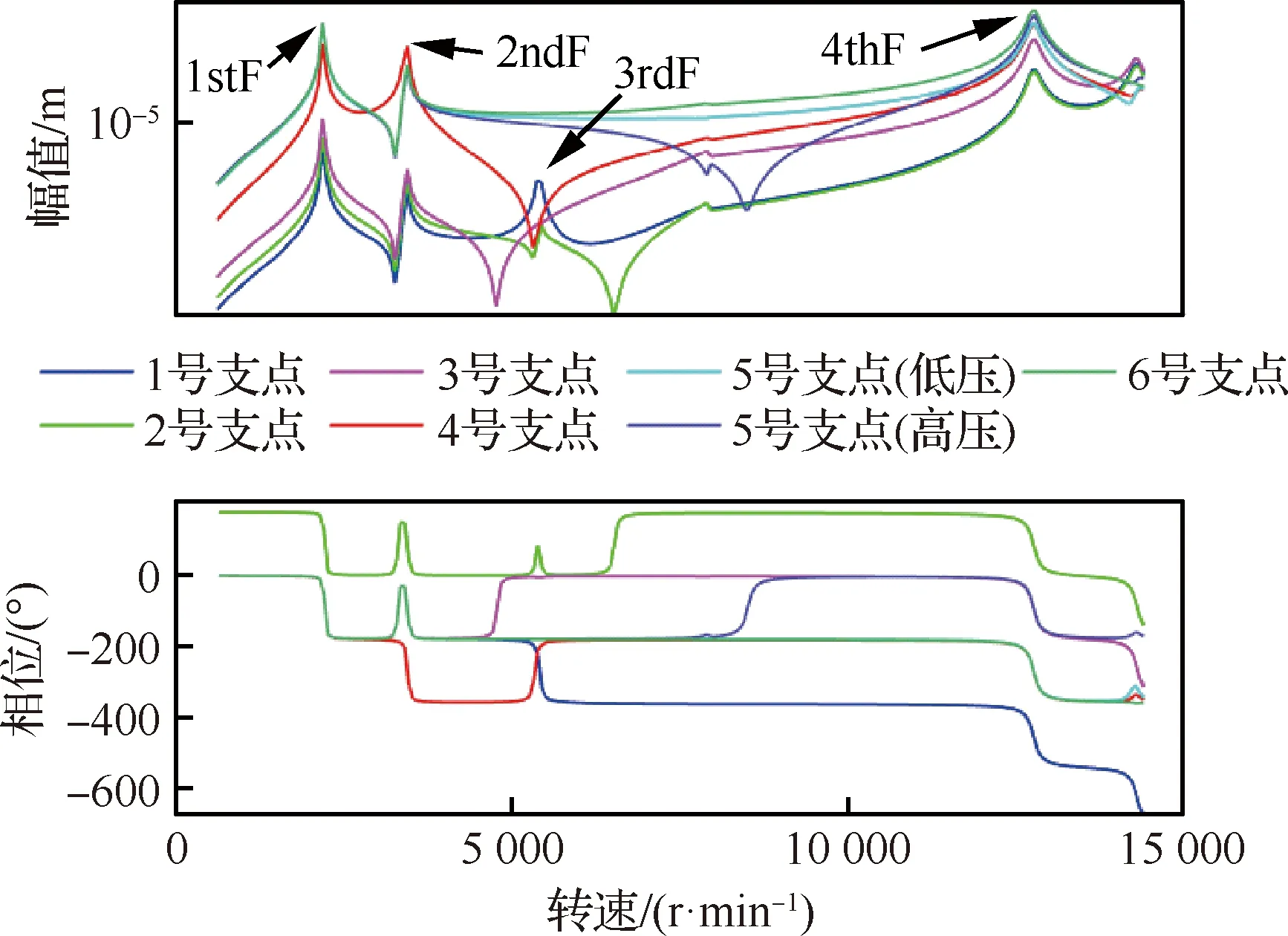
圖6 高壓轉(zhuǎn)子激勵(lì)時(shí)雙轉(zhuǎn)子各支點(diǎn)的響應(yīng)

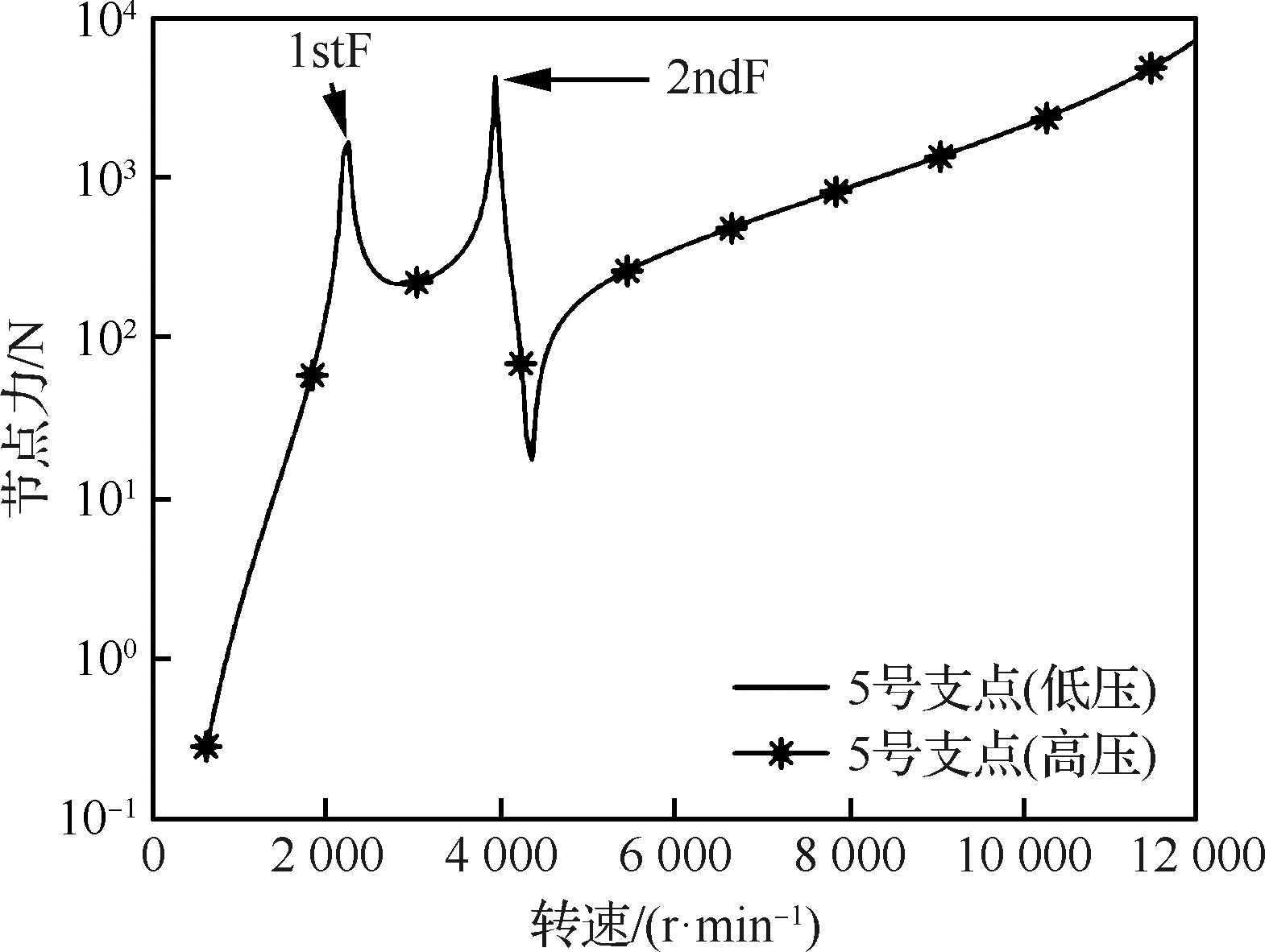
圖7 低壓渦輪存在不平衡激勵(lì)時(shí)5號(hào)支點(diǎn)節(jié)點(diǎn)力

圖8 高壓渦輪存在不平衡激勵(lì)時(shí)5號(hào)支點(diǎn)節(jié)點(diǎn)力

為了分析雙轉(zhuǎn)子中低壓轉(zhuǎn)子(高壓轉(zhuǎn)子)激勵(lì)時(shí)受高壓轉(zhuǎn)子(低壓轉(zhuǎn)子)耦合作用的影響程度，通過(guò)計(jì)算低壓轉(zhuǎn)子(高壓轉(zhuǎn)子)單轉(zhuǎn)子有相同不平衡量時(shí)的不平衡響應(yīng)，并繪制在整個(gè)轉(zhuǎn)速范圍內(nèi)的低壓轉(zhuǎn)子(高壓轉(zhuǎn)子)-支點(diǎn)應(yīng)變能占比變化量如圖9、圖10所示。

可以看出，雙轉(zhuǎn)子耦合作用較強(qiáng)的位置不一定與轉(zhuǎn)子響應(yīng)較大的位置一致。例如，在圖5中的位移響應(yīng)峰值位置，轉(zhuǎn)子-支點(diǎn)的應(yīng)變能變化曲線(圖9)并未達(dá)到峰值，如圖9中低壓轉(zhuǎn)子支點(diǎn)在整個(gè)轉(zhuǎn)速范圍內(nèi)的受耦合程度較大的位置為1stF與2ndF之間、3rdF之后；在圖6中的位移響應(yīng)峰值位置，圖10中高壓轉(zhuǎn)子-支點(diǎn)在整個(gè)轉(zhuǎn)速范圍內(nèi)的受耦合程度較大的位置為2ndF與3rdF之間。圖9中除低壓渦輪、6號(hào)支點(diǎn)應(yīng)變能占比變化量較大外，其余部分在整個(gè)轉(zhuǎn)速范圍內(nèi)變化均較小，幾乎為0。

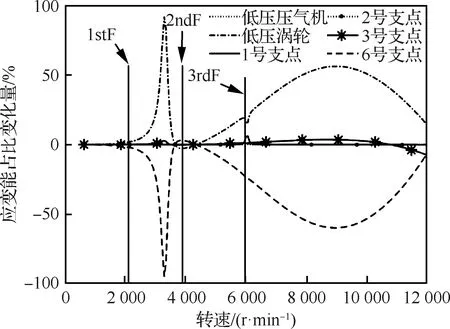
圖9 低壓渦輪激勵(lì)時(shí)低壓轉(zhuǎn)子應(yīng)變能占比變化量隨轉(zhuǎn)速變化曲線

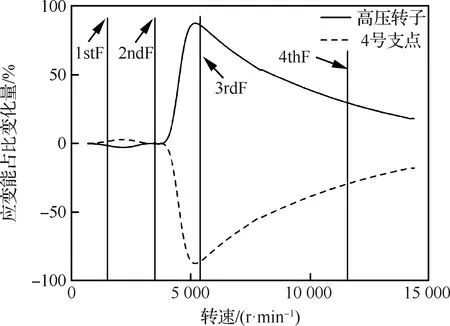
圖10 高壓渦輪激勵(lì)時(shí)高壓轉(zhuǎn)子應(yīng)變能占比變化量隨轉(zhuǎn)速變化曲線

而當(dāng)?shù)蛪簤簹鈾C(jī)1級(jí)葉盤有相同不平衡量時(shí)，低壓轉(zhuǎn)子對(duì)應(yīng)的應(yīng)變能占比變化量如圖11所示，轉(zhuǎn)子、支點(diǎn)的變化量均很小，可以看出雙轉(zhuǎn)子系統(tǒng)的耦合作用對(duì)低壓壓氣機(jī)不平衡量不敏感。從圖2中的臨界轉(zhuǎn)速所對(duì)應(yīng)的振型也能得到類似的定性結(jié)論。圖11中除1號(hào)支點(diǎn)、6號(hào)支點(diǎn)應(yīng)變能占比變化量相對(duì)較大外，其余部分在整個(gè)轉(zhuǎn)速范圍內(nèi)變化接近于0。

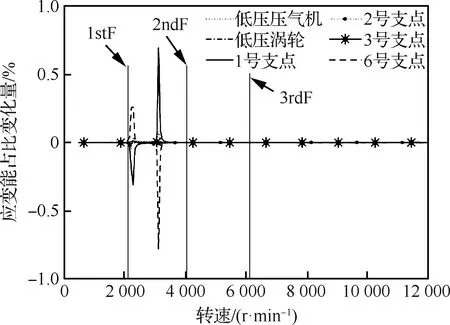
圖11 低壓壓氣機(jī)激勵(lì)時(shí)低壓轉(zhuǎn)子應(yīng)變能占比變化量隨轉(zhuǎn)速變化曲線

為了進(jìn)一步分析在不同轉(zhuǎn)速下轉(zhuǎn)子不同位置的應(yīng)變能變化，在圖9、圖10所示的轉(zhuǎn)子各部分隨轉(zhuǎn)速變化的應(yīng)變能占比變化量圖的基礎(chǔ)上增加第三維坐標(biāo)-轉(zhuǎn)子各單元位置，可以分別得到低壓轉(zhuǎn)子(或高壓)激勵(lì)時(shí)的低壓(或高壓)轉(zhuǎn)子各單元應(yīng)變能占比變化量隨轉(zhuǎn)速變化曲線如圖12、圖13所示。在某一轉(zhuǎn)速下沿該圖縱坐標(biāo)方向看，為該轉(zhuǎn)速下轉(zhuǎn)子上各單元的應(yīng)變能變化；若沿該圖橫坐標(biāo)方向看，為特定單元的應(yīng)變能變化隨轉(zhuǎn)速變化情況。

由圖12、圖13可知，在整個(gè)轉(zhuǎn)速范圍內(nèi)，應(yīng)變能變化較大的位置為5號(hào)支點(diǎn)所在的低壓渦輪軸附近、高壓渦輪及高壓渦輪軸附近，說(shuō)明這些位置受雙轉(zhuǎn)子耦合作用較大，在轉(zhuǎn)子系統(tǒng)設(shè)計(jì)時(shí)應(yīng)重點(diǎn)關(guān)注。此外雙轉(zhuǎn)子耦合作用較強(qiáng)的位置不一定在轉(zhuǎn)子響應(yīng)較大的位置，這與圖9、圖10的結(jié)論一致。

圖12 低壓轉(zhuǎn)子激勵(lì)時(shí)低壓轉(zhuǎn)子各單元應(yīng)變能占比變化量隨轉(zhuǎn)速變化曲線

圖13 高壓轉(zhuǎn)子激勵(lì)時(shí)高壓轉(zhuǎn)子各單元應(yīng)變能占比變化量隨轉(zhuǎn)速變化曲線

3 結(jié) 論

1) 雙轉(zhuǎn)子的耦合作用對(duì)振型及相應(yīng)的臨界轉(zhuǎn)速影響主要有3種情況。一是由于中介軸承附近振動(dòng)較小使得耦合作用較弱而幾乎無(wú)影響，表現(xiàn)為單轉(zhuǎn)子的部分模態(tài)振型會(huì)在雙轉(zhuǎn)子模態(tài)振型中出現(xiàn)，且為一一對(duì)應(yīng)關(guān)系，振型相似性極高，臨界轉(zhuǎn)速相對(duì)變化率較小，應(yīng)變能分布變化小；二是由于其一轉(zhuǎn)子振型變化較大而另一轉(zhuǎn)子改變較小導(dǎo)致振型重復(fù)出現(xiàn)，表現(xiàn)為單轉(zhuǎn)子的一些模態(tài)振型會(huì)在雙轉(zhuǎn)子模態(tài)振型中重復(fù)出現(xiàn)，且振型相似性較高，臨界轉(zhuǎn)速相對(duì)變化率可能較大，應(yīng)變能分布變化較小；三是由于其一轉(zhuǎn)子振型變化較大導(dǎo)致另一轉(zhuǎn)子支承特性改變而出現(xiàn)耦合振型，特別是高壓轉(zhuǎn)子，表現(xiàn)為雙轉(zhuǎn)子中單階模態(tài)振型與單獨(dú)轉(zhuǎn)子的兩階或多階模態(tài)振型有一定相似性，且與這些模態(tài)振型的置信因子之和接近1，此時(shí)，對(duì)應(yīng)的臨界轉(zhuǎn)速以及應(yīng)變能分布變化較為復(fù)雜，需具體分析。

2) 通過(guò)全轉(zhuǎn)速范圍內(nèi)的穩(wěn)態(tài)不平衡響應(yīng)分析發(fā)現(xiàn)，中介軸承在臨界轉(zhuǎn)速位置受力最大，而應(yīng)變能分布變化最大的轉(zhuǎn)速位置與系統(tǒng)臨界轉(zhuǎn)速位置不一致。同時(shí)受不平衡激勵(lì)位置影響，耦合作用對(duì)渦輪位置的不平衡量更為敏感。進(jìn)一步通過(guò)全轉(zhuǎn)速范圍內(nèi)各單元應(yīng)變能占比變化量隨轉(zhuǎn)速變化曲線可以詳細(xì)分析特定不平衡激勵(lì)下應(yīng)變能分布變化情況，為轉(zhuǎn)子系統(tǒng)設(shè)計(jì)或振動(dòng)分析提供參考。