基于QSS的自適應多步校正算法及其在柔性航天器動力學中的應用
李志華,李廣,沈漢武,樊志華
杭州電子科技大學 機械工程學院,杭州 310018
具有剛性、非線性和強耦合特點的動力學系統廣泛存在于機械、土木、航空航天等領域。例如航天器系統,由于存在柔性件振動變形以及大范圍運動位移和小范圍振動位移之間的相互耦合,其動力學模型就呈現剛性、非線性和強耦合的特點[1-2]。對這類剛性系統進行仿真求解十分困難,而對其動力學模型的精確高效求解是對其進行精確控制的基礎[3]。目前數值求解的方法主要包括直接數值求解法和降階求解法。
直接數值求解法以Wilson-θ和Newmark為主[4-6],該方法需要調用迭代算法,計算成本高、仿真效率低,且仿真精度的提高存在局限性。降階求解法通過將動力學方程轉化為低階的常微分方程,然后采用傳統的數值積分方法進行求解,相比于直接數值求解法,它在仿真效率、計算成本以及仿真精度上均存在一定的優勢。
降階求解法所使用的傳統數值積分方法有Euler法、Adams多步法、龍格庫塔法和Gear法等。Euler和龍格庫塔法屬于單步法,Gear和Adams法屬于多步法。其中,Euler法是最簡單的數值方法,它在求解剛性問題時,需要顯著地減少積分步長,以保持穩定性,但這會導致誤差的積累,不利于剛性問題的求解;Gear法初始值較難確定,求解高振蕩方程時會失效,同時方程的階數一般較大[7];隱式的龍格庫塔方法求解剛性問題時穩定性好、精度高,但是s階的龍格庫塔法在求解一個r維的剛性問題時,每步都需要求解一個由s×r個方程聯立的方程組,在實際工程應用中,其計算量過于龐大,導致實際求解時的效率不高[8]。相比于龍格庫塔方法,Adams多步法的優點是計算格式簡單、每步計算量相對較小,同時也具備較高的求解精度,缺點是使用隱式Adams多步法在求解剛性問題時,相比于顯式算法仍會有較大的計算量。由此可見,單純地使用傳統的隱式算法或顯式算法來求解動力學中的剛性問題,都存在著一定的困難。
量化狀態系統(Quantized State System,QSS)算法是一種新的數值積分方法,由Zeigler和Lee[9]首次提出,并由 Kofman和Junco[10]首次算法實現。與基于時間離散的傳統方法不同,QSS將所有的狀態變量離散化,以“量子”代替“步長”,通過計算所有狀態變量每次變化一個量子所需要的最短時間,來進行下一步積分的推進。在求解非剛性問題時,QSS算法穩定性強,同時計算過程不需要迭代,因此仿真效率得到了極大的提高。QSS的狀態變量軌跡是分段線性的,其求解精度相對于傳統算法并不占優勢。為了提高其算法精度,QSS2和QSS3采用高次曲線來對狀態變量變化的時間進行估計,利用狀態變量的高階導數來改進近似值[11-13]。在求解非剛性問題時,QSS2和QSS3的求解精度得到了提高,要好于QSS。但在求解剛性問題時,QSS、QSS2、QSS3均存在可能的數值振蕩現象;此外,在求解剛性問題時,QSS2和QSS3的求解效率要遠低于QSS[12-14]。
為了解決QSS求解剛性問題時所出現的數值振蕩現象,Migoni和Kofman[15]提出了BQSS(Backward QSS)算法,但該算法在求解非線性剛性問題時,由于誤差范圍較大,可能會出現“假性平衡”現象,影響仿真的推進。后續Migoni提出了一階LIQSS(Linearly Implicit QSS)算法,它將量化變量q看作狀態變量x的預測值,避免了某些擾動項對求解剛性問題所造成的影響。但是LIQSS算法要求剛性問題中的雅可比矩陣的對角線要存在較大的元素,否則可能會出現“假性振蕩”現象,會對仿真求解的精度和穩定性造成較大的影響[16]。之后,Migoni等[17]又提出了改進的LIQSS算法,但在求解剛性較大的微分方程時,仍然存在求解效率較低或者無法求解的缺陷。國內學者目前研究還較少,只有文獻[18-20]對QSS算法進行了初步應用。
本文將QSS算法和隱式多步法相結合,提出一種自適應多步校正算法。通過對柔性航天器動力學的仿真求解,驗證了算法的可行性。從仿真精度和效率2方面,將該算法與幾種典型的傳統算法(ODE23tb、ODE15s、ODE45等)以及QSS算法進行了性能對比。
1 量化狀態系統
常微分方程表示的狀態方程系統為

(1)
式中:x(t)∈Rn為系統的狀態向量;u(t)為輸入向量,QSS算法將式(1)方程重新定義為
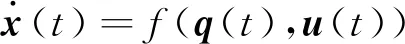
(2)
式中:q(t)為系統的量化變量,每個量化變量qi(t)均通過式(3)的遲滯量化函數得到,
(3)
式中:ΔQi為量子;qi(t-)為上一次計算的量化變量。
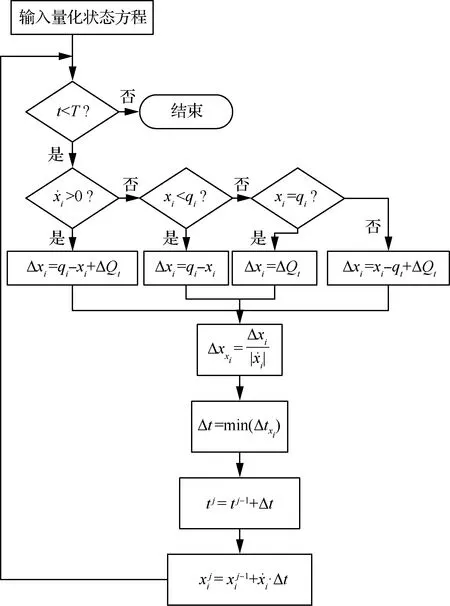
圖1 QSS算法的流程圖
2 自適應多步校正算法
2.1 AMCQSS
本文提出的自適應多步校正算法(Adaptive Multi-step Correction algorithm based on QSS,AMCQSS)旨在有效提高仿真精度的同時保證仿真的效率,并且拓展QSS算法求解剛性問題的應用范圍。本算法以QSS算法為基礎、同時結合了隱式多步法的思想:QSS算法作為顯式算法,具有較好的全局誤差控制特性,且其求解過程不需要迭代,保證了仿真求解的效率;多步法能夠充分運用前面已經求得的多個點的信息來校正目前所需求解的值;同時本算法還可以根據計算過程中求得的導數差值來自行選擇二步法或三步法,以獲得更高的求解精度;此外本算法將量化變量值作為狀態變量的預測值,來扼制剛性系統中可能出現的仿真數值振蕩,以提高算法的穩定性和仿真求解的精度。
AMCQSS方法將式(1)近似為
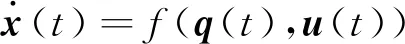
(4)
式中:q為量化變量,這里作為求x的一階導數的預測值。
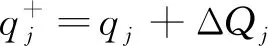
(5)
(6)
此時,狀態變量仿真推進時間為
(7)
式中:k為仿真執行的步數。
當k≤2時,狀態變量值的計算公式為
(8)
當k>2時,AMCQSS算法使用多步法思想對第k步的狀態變量進行校正,本算法中融入了隱式多步法中的二步法和三步法思想。在求解剛性問題時,系統方程的曲線可能會在某一點突變,此時的曲線斜率會劇烈變化,該點的導數與前幾點的導數相比較會產生較大的變化,這時使用二步法或三步法思想來對該點的狀態變量進行校正,其校正求得的2個狀態變量在數值上可能差距較大。為了保證求解的精度,將二步法與三步法求得的導數分別和第k步導數相比,選擇導數值與第k步導數值相差較小的多步法。此時所選擇的多步法校正后得到的第k步狀態變量值是位于另一種多步法校正后得到的狀態變量值和校正前的狀態變量值之間,無論該點真實情況偏向于哪一邊,均不會出現偏差過大的情況,這樣可以有效地控制誤差,避免誤差積累影響到之后的仿真推進。導數差計算公式為
(9)
根據差值選擇狀態變量的計算公式
(10)
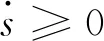
(11)
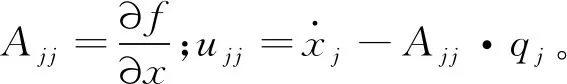
(12)
然后按式(7)~式(10)計算,最終系統每次推進的仿真時間為
Δt=min(Δtj)
(13)
2.2 AMCQSS算法的實現
算法實現(以偽代碼的形式)如下:
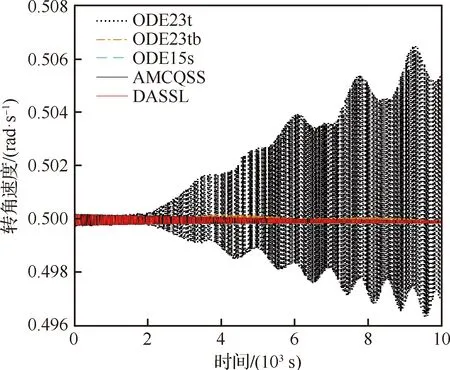
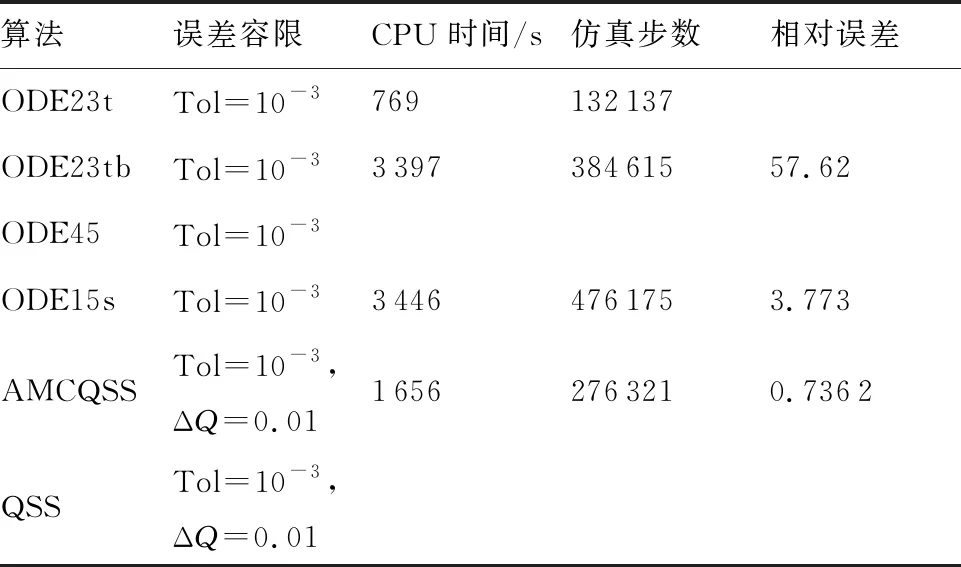
While(t for until (|xj-qj=ΔQj|) qj=xj+ΔQj qj=xj-ΔQj if (k≤2) then else else end if end if else if (k≤2)then else else end if end if end for Δt=min(Δtj) ∥(系統每推進一步,仿真的時間取狀態變量的最小躍遷時間) end while 2.3.1 收斂性 (14) 假設λ(t)和λ1(t)分別為式(4)和式(14)的初始解,且λ(0)=λ1(0),則 f(λ(τ),u(τ))]dτ (15) 根據Euclidean范數,可得 (16) 設定M為函數f的Lipschitz常數,則式(16)有 MtΔx (17) 其中λ(t),λi(t)均連續,且M為正數,則根據Gronwall-Bellman不等式將式(17)改為 (18) 其中M和t不依賴于Δx,則 (19) 由式(19)可得,AMCQSS算法具有收斂性。 2.3.2 穩定性 假設式(1)是線性時不變系統,可將式(1)改寫為 (20) 使用AMCQSS算法可將式(20)寫成 (21) 式中:A為Hurwitz矩陣;B為系統矩陣,則AMCQSS的誤差為 |e(t)|≤|V|·|Re(Λ)-1·Λ|·|V-1|·ΔQ (22) 式中:Λ為矩陣A的特征值的對角矩陣;V為矩陣A的特征向量矩陣;Re為取復數的實數部分。 由式(22)可得,AMCQSS算法的全局誤差總是有界,因此AMCQSS算法具有穩定性。 圖2是柔性航天器中的柔性多體衛星力學模型,將衛星本體(星體)假設為無變形的中心剛體、忽略鉸連接處的摩擦力、將太陽帆板視為固連在星體上的一塊均質薄板且相對星體無轉動[23-26]。 圖2 柔性多體衛星系統力學模型 圖2中,B為星體,Ai表示為與星體連接的第i個撓性附件。引入與軌道參考坐標系等同的慣性坐標系Oxyz、星體固連坐標系Oxbybzb和撓性附件固連坐標系Pxiyizi,忽略衛星自身運動相對標稱位置的小擾動[25]。Ob為星體質心;Pi為撓性附件與星體的連接點;Rb,k為點O到星體質量元dmb,k的矢徑;rb,k為點Ob到質量元dmb,k的矢徑;Rai,j為點O到質量元dmai,j的矢徑;xO為星體質心相對于點O的小位移攝動;rpi為質心點Ob和點Pi之間的矢徑;rai,j為Pi到撓性附件質量元dmai,j上的矢徑;δai,j為dmai,j的振動變形矢量[25-27]。 使用模態綜合—混合坐標法以及Euler-Lagrange方程對柔性多體衛星進行動力學建模,并將其轉化成常微分方程形式(由于篇幅所限,本文不進行詳細推導,具體過程可參考文獻[25-26]): (23) 式中:ΛL和ΛR分別為左右帆板的模態剛度陣;FsaiL和FsaiR分別為整星轉動時左右帆板的剛柔耦合陣;FtaiL和FtaiR分別為整星平動時左右帆板的剛柔耦合陣。為了方便計算,記FsaiL1為FsaiL矩陣的第1行,FsaiL2為FsaiL矩陣的第2行,以此類推。M為衛星質量矩陣;As為衛星的姿態變換陣(歐拉角轉動順序為2-1-3): 其中:cos表示為c;sin表示為s;α為繞慣性系y軸旋轉α角,得到過渡坐標系x1y1z1;θ為繞過渡坐標系x1y1z1中x1軸旋轉θ角,得到過渡坐標系x2y2z2;φ為繞過渡坐標系x2y2z2中z2軸旋轉φ角,得到星體固連坐標系xbybzb,完成慣性系到星體固連坐標系的轉換。 ΛR=ΛL=diag{900,14 400,16 900,250 000,280 900,360 000},左右帆板的剛柔耦合陣(單位為kg1/2·m)為 FtaiR= FtaiL= ⑤ 系統各個狀態變量的相對誤差計算公式為 (24) 式中:um[k]為各個算法求得的狀態變量值;udassl[k]為DASSL求解器在誤差設定為10-9的情況下求得的狀態變量值,在此作為基準值[28]。 對柔性多體衛星動力學模型進行仿真求解,得到圖3~圖5所示的衛星角度及角速度變化圖,其中QSS和ODE45算法無解。從圖3~圖5中可以看出:ODE23t出現了明顯的發散,說明ODE23t不適用于該剛性問題的求解;ODE23tb雖然最終結果趨于穩定,但中間過程上下波動較大,其求解剛性問題的穩定性較差;AMCQSS和ODE15s 2種算法波動均很小,且整個過程收斂性和穩定性均較好。由表1可以看出,其中求解結果最好的傳統算法是ODE15s;相比于ODE15s,AMCQSS算法在求解效率上提高了1倍多,在求解精度上提高了4倍多。 圖3 衛星α角轉角變化圖 圖4 衛星θ角轉角變化圖 圖5 衛星φ角轉角速度 表1 柔性多體衛星動力學方程的仿真結果 針對具有剛性、非線性和強耦合特點的動力學求解難題,本文提出了一種有別于傳統方法的自適應多步校正算法AMCQSS,通過對柔性航天器動力學的仿真求解,得到以下結論: 1) ODE45和QSS是顯式算法,在求解剛性問題時,會出現無解情況,很難滿足實際工程中剛性問題的求解需要。 2) ODE23t和ODE23tb算法穩定性較差,不適于強剛性問題的求解。 3) ODE15s和AMCQSS算法穩定性和收斂性均較好,但AMCQSS算法的求解精度和效率更高,算法性能優于QSS算法和ODE15s等傳統算法。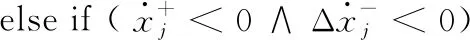
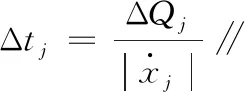
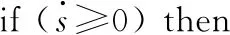
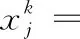
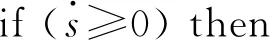
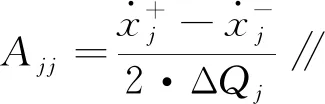
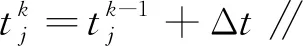
2.3 算法的收斂性與穩定性分析
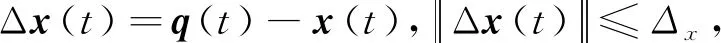
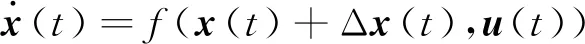
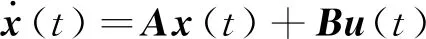
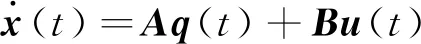
3 柔性航天器的動力學模型

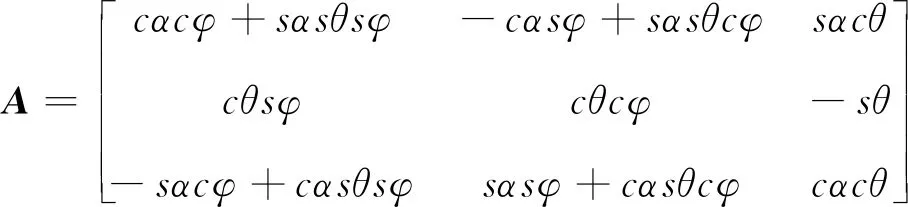
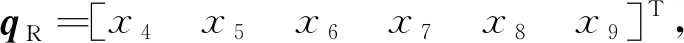
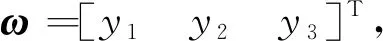
4 仿 真
4.1 仿真背景
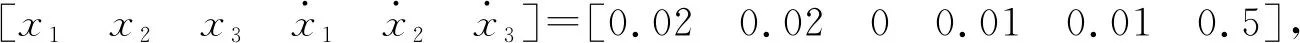



4.2 仿真結果對比分析


5 結 論

