基于稀疏貝葉斯學習的字典失配雜波空時譜估計方法
章濤,鐘倫瓏,來燃,郭駿騁
中國民航大學 天津市智能信號與圖像處理重點實驗室,天津 300300
空時自適應處理(Space-Time Adaptive Processing, STAP)是機載陣列雷達抑制雜波的一種有效方法[1-2]。STAP的雜波抑制性能主要取決于雜波協方差矩陣(Clutter-plus-noise Covariance Matrix, CCM)的估計精度。傳統STAP方法采用統計估計的方法獲得CCM估計值,若需保證輸出信雜比相較最優值下降不超過3 dB,則至少需要系統自由度2倍數量的獨立同分布(Independent Identically Distributed, IID)雜波樣本[3]。然而在實際系統中,當雜波呈現非平穩或非均勻特性時,很難獲得足夠的IID樣本,進而使得STAP雜波抑制性能嚴重損失[4]。
為了減少STAP所需雜波樣本數量,研究人員提出了多種方法,主要包括降維STAP方法和降秩STAP方法。降維STAP方法利用與數據無關的變換降低接收數據維數,使得所需雜波樣本數量為降維后數據維數的2倍,主要方法包括:輔助通道處理(Auxiliary Channel Processing, ACP)方法[5]、擴展因子化(Extended Factored Approach, EFA)方法[6]、廣義多波束(Generalized Multiple Beams, GMB)方法[7]等,但這類方法不可避免地存在系統自由度損失。降秩STAP方法則利用與數據有關的變換對接收數據進行處理,使得所需雜波樣本數降低為雜波秩的2倍,主要方法包括:正交投影處理(Orthogonal Projection Processor, OPP)方法[3]、最小功率特征對消(Minimum Power Eigen canceller, MPE)方法[8]、多級維納濾波(Multistage Winer Filter, MWF)方法[9]等,但是這類方法的性能依賴于雜波秩,在實際雜波環境中很難準確估計雜波秩。
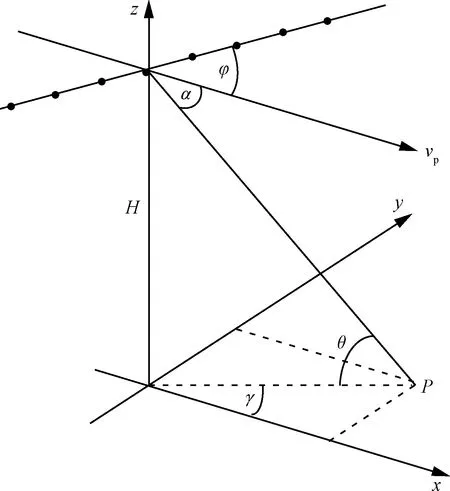
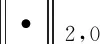
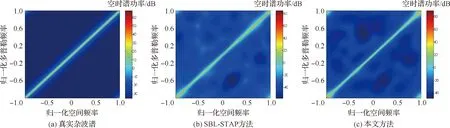
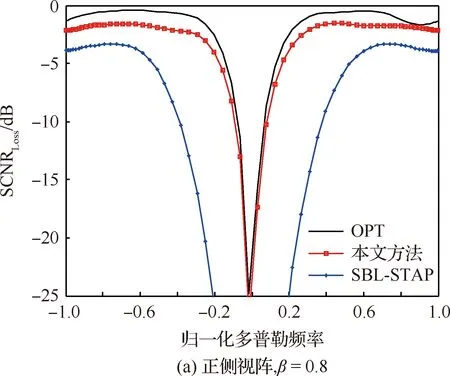
近年來,稀疏恢復方法在信號處理領域快速發展[10-11]。由于稀疏恢復方法可以使用很少樣本精確地恢復未知稀疏信號,已成為機載雷達雜波抑制的研究熱點[12-13]。目前比較有代表性的雜波空時譜稀疏恢復方法包括:文獻[14]提出了利用1范數最小化實現空時譜稀疏恢復的凸優化方法。文獻[15-17]提出了基于p范數(0 稀疏恢復STAP方法將雜波信號看作在某些已知基向量下是稀疏的,這些基向量被稱為稀疏恢復字典。由于空時平面被離散地劃分為若干個網格點來構建空時導向矢量字典,離散化的字典與連續的雜波譜參數間的誤差問題被稱作字典失配問題,嚴重影響稀疏恢復效果。在正側視陣情況下,若稀疏恢復空時平面網格劃分與雜波脊斜率不匹配;或是當陣列為非正側視架設,雜波脊呈曲線形式時,則雜波大多不會位于預先離散化的空時平面網格點上,字典失配將嚴重影響稀疏恢復STAP的雜波抑制性能。雖然增加空時導向矢量劃分密度可以減少字典失配的影響[19],但字典網格間隔越小,空時導向矢量的相關性越強,會導致稀疏恢復性能下降,而且計算量也將大幅增加[10]。 目前,針對稀疏恢復中字典失配問題的研究主要集中在一維離散參數字典的補償方面,如:文獻[20]提出了一種稀疏總體最小二乘(Sparse Total Least-Squares, STLS)方法,結合動態字典模型解決一維波達方向(Direction of Arrival, DOA)估計中的字典失配問題。文獻[21]提出利用基追蹤方法解決DOA估計中的字典失配問題。為了避免正則化參數難以確定的問題,文獻[22] 提出了一種利用動態字典解決字典失配問題的稀疏貝葉斯學習(Off-Gird Sparse Bayesian Inference, OGSBI)方法,但該方法僅能處理一維離散參數字典失配問題,不能直接用于存在二維字典失配的雜波空時譜稀疏恢復。目前針對雜波空時譜稀疏恢復中二維離散參數字典失配問題的研究還比較少,且有一定的適用局限性。例如,文獻[23]在2013年首次提出了雜波空時譜估計中存在字典失配問題,并給出了一種利用字典學習的失配補償方法,但該方法僅適用于正側視陣情況。文獻[24]提出了利用載機平臺運動參數獲得雜波脊先驗信息后細化字典間隔來解決字典失配問題的方法,但這種方法依賴載機平臺傳感器,有些情況并不適用。文獻[25]提出了基于正交匹配追蹤(Orthogonal Matching Pursuit, OMP)的方法,通過梯度下降方法尋找與真實模型匹配的字典向量來解決字典失配問題,但OMP方法的性能對參數選擇依賴性較高。 針對目前已有的字典失配情況下稀疏恢復STAP算法存在僅適用于正側視陣、依賴機載平臺其他傳感器、算法性能對參數選擇敏感等問題,本文將OGSBI方法擴展到二維字典失配的情況,提出了一種解決空時二維字典失配的稀疏貝葉斯學習STAP方法。本方法的主要創新性包括:① 針 對空時二維參數字典失配,建立了一種利用二維泰勒級數的空時二維字典失配誤差動態模型;② 將空時二維字典失配誤差作為超參數,給出了期望最大化(Expectation-Maximization, EM)方法迭代估計公式,進而修正空時二維參數字典失配誤差, 最后利用修正后的空時導向矢量字典估計雜波協方差矩陣及雜波空時譜。實驗表明,本文方法能夠有效提高雜波譜稀疏恢復精度,STAP處理性能優于已有字典預先離散化處理的稀疏貝葉斯學習STAP算法。 考慮采用均勻線陣的機載陣列雷達,如圖1所示,陣列天線由M個陣元組成,陣元間距d=λ/2,λ為雷達工作波長;H為載機平臺高度;vp為速度,且沿x軸運動;α為雜波散射點P與飛行方向間的夾角;θ和γ分別為俯仰角和方位角;φ為陣列軸線與飛行方向間的夾角,即當φ=0°時為正側視陣模式,φ=90°為正前視陣模式。 圖1 機載雷達陣列幾何結構 雷達在每個相干處理周期內發射N個脈沖,脈沖重復頻率為fr。當不存在距離模糊時,對于不存在目標的距離單元的回波進行采樣可以獲得一個雜波觀測矢量數據(通常稱為一個空時快拍數據)x∈CNM×1 x=xc+n (1) 式中:xc為雜波分量;n為噪聲分量。每個距離單元的雜波可以看成是多個雜波散射體空時響應的疊加,即 (2) 式中:Nc表示雜波散射體數量;ai、fd,i和fs,i分別表示復幅度、多普勒頻率和空間頻率。s(fd,i,fs,i)∈CNM×1稱為空時導向矢量,即s(fd,i,fs,i)=sd,i(fd,i)?ss,i(fs,i),?表示Kronecker積運算。其中: 空間導向矢量ss,i(fs,i)定義為 ss,i(fs,i)=[1,exp(j2πfs,i),…, exp(j2π(M-1)fs,i)]T (3) 時間導向矢量sd,i(fd,i)定義為 sd,i(fd,i)=[1,exp(j2πfd,i),…, exp(j2π(N-1)fd,i)]T (4) 空間頻率fs,i滿足 fs,i=cos(γi-φ) (5) 多普勒頻率fd,i滿足 (6) 在歸一化空間頻率和多普勒頻率構成的空時平面上,雜波脊的斜率(折疊系數)為 (7) CCM定義為 R=E(xxH) (8) 在噪聲向量n假設為零均值高斯分布的情況下,基于最大信雜噪比(Signal-to-Clutter-plus-Noise Ratio, SCNR)準則,可以得到自適應權矢量的STAP輸出為 y=wHx (9) 式中:自適應權矢量w可以通過CCM計算獲得,即 (10) 其中:st(fd,fs)為待檢測單元的空時導向矢量。由于CCM未知,實際系統中可以通過與目標檢測單元雜波分布相同的雜波樣本計算CCM的估計值,如 (11) 其中:訓練樣本數L需大于系統自由度的2倍,這種方法稱作采樣矩陣求逆(Sample Matrix Inversion, SMI) STAP方法[1]。但對于非均勻、非平穩的雜波環境不同距離單元雜波數據難以構成足夠的IID樣本,因此這種方法在有些情況下并不適用[12-13]。 基于雜波譜稀疏恢復的STAP方法將上述方法中的CCM估計通過稀疏恢復的方法實現,可有效減少所需IID雜波訓練樣本數[12-13]。這類方法首先將雜波譜空時平面劃分為Ns×Nd的網格。其中,Ns=ρsM,Nd=ρdN,ρs和ρd為網格劃分系數,且ρs>1,ρd>1。網格點所對應的空時導向矢量集合可以表示為 Ψ=[ψ1,ψ2,…,ψNs×Nd]=Sd?Ss (12) 式(12)在稀疏恢復STAP中被稱為空時導向矢量字典,其中 Ss=[ss,1,ss,2,…,ss,Ns]∈CM×Ns (13) Sd=[sd,1,sd,2,…,sd,Nd]∈CN×Nd (14) 單快拍(Single Measurement Vector, SMV)雜波樣本數據x的稀疏恢復模型可以表示為 x=Ψa+n (15) 式中:a=[a1,a2,…,aNsNd]T為稀疏恢復支撐集向量,其每一個非零元素表示一個對應的雜波單元。通過稀疏恢復理論,支撐集向量a可以通過下面最優化方法獲得 (16) 通過稀疏恢復方法獲得支撐集向量a后,CCM矩陣可通過式(17)重構獲得 (17) 為了提高稀疏恢復性能,可以利用多快拍(Multiple Measurement Vector, MMV)雜波樣本數據進行聯合稀疏恢復。K個雜波樣本數據X=[x1,x2,…,xK]∈CNM×K可以表示為 X=ΨA+N (18) 式中:A=[a1,a2,…,aK]為稀疏恢復的支撐集矩陣,其每個非零行表示一個對應的雜波單元;N=[n1,n2,…,nK]為噪聲矩陣。通過聯合稀疏恢復理論,支撐集矩陣A可以通過式(19)最優化方法獲得 (19) 稀疏恢復STAP方法使用的空時導向矢量字典中空間頻率和多普勒頻率等間隔離散地分布在空時平面上。對于正側視陣,且折疊系數β=1時,雜波脊位于空時平面對角線位置,正好位于空時平面網格點上,如圖2(a)所示,字典中空時導向矢量可以準確地與雜波單元對應,此時不存在字典失配問題,STAP處理性能較好。當折疊系數β≠1即雜波脊不在空時平面對角線上,如圖2(b)所示,或工作在非正側視陣情況,雜波脊在空時平面上呈現曲線形式時,如圖2(c)所示,可以看出雜波單元通常不能與空時導向矢量對應,字典失配將嚴重影響雜波譜稀疏恢復性能。 圖2 雜波脊在空時平面上的分布示意圖 (20) 利用空時二維動態字典估計字典失配誤差Δfd和Δfs后,可得到失配補償后的字典Φ=[Φ1,Φ2,…,ΦNsNd],即 Φ(Δfd,Δfs)=Ψ+Fdiag(Δfd)+Gdiag(Δfs) (21) 式中:Ψ為式(12)定義的失配字典。 (22) (23) (24) (25) 估計字典失配誤差進行補償后,式(15)改寫為 x=Φ(Δfd,Δfs)a+n (26) 式(18)可以改寫為 X=Φ(Δfd,Δfs)A+N (27) 本節以式(27)表示的MMV模型,給出字典失配誤差估計及空時譜估計的稀疏貝葉斯學習算法,式(26)表示的SMV模型可由MMV模型方法中快拍數設置K=1得到。 噪聲向量N假設為零均值復高斯白噪聲,則 (28) p(X|A,Δfd,Δfs,λ0)= (29) 式中:λ0未知,假設服從伽馬先驗分布,即 p(λ0|c0,d0)=Γ(λ0|c0,d0) (30) 為了保證獲得廣泛的超先驗,一般假設c0→0,d0→0,例如取c0=1×10-4,d0=1×10-4。 稀疏支撐集A=[a1,a2,…,aK]的各列獨立,且假設服從復高斯先驗分布,即 (31) 式中:Λ=diag(λ),λ假設為NsNd維獨立伽馬分布,即 (32) 式中:超參數ρ=1×10-3。 字典失配誤差Δfd和Δfs假設服從NsNd維均勻分布,即 Δfd~U([-rd/2,rd/2]NsNd) (33) Δfs~U([-rs/2,rs/2]NsNd) (34) 式中:rd和rs分別為離散字典的歸一化多普勒頻率間隔和歸一化空間頻率間隔。 由于后驗分布p(A,Δfd,Δfs,λ0,λ|X)不能顯式給出,將A當作隱變量,則其后驗分布滿足: (35) 式中: μk=λ0ΣΦHxk (36) Σ=(λ0ΦHΦ+Λ-1)-1 (37) 由式(35)可知,信號支撐集矩陣A的稀疏解與μk和Σ的稀疏解一一對應。計算μk和Σ的稀疏解需要對超參數Δfd,Δfs,λ0和λ進行估計。根據稀疏貝葉斯理論,超參數可以用最大后驗方法估計,即最大化p(Δfd,Δfs,λ0,λ|X),由于p(X)與上述超參數無關,因此最大化p(Δfd,Δfs,λ0,λ|X)與最大化p(Δfd,Δfs,λ0,λ,X)=p(Δfd,Δfs,λ0,λ|X)p(X)等價,并且有 p(A,X,Δfd,Δfs,λ0,λ)= p(X|A,Δfd,Δfs,λ0)p(A|λ)p(λ)p(λ0)· p(Δfd)p(Δfs) (38) 利用EM方法迭代更新超參數λ和λ0,具體推導過程可參見文獻[24],λ和λ0的更新方程分別為 n=1,2,…,NsNd (39) (40) tr{(Ψ+Fdiag(Δfd)+Gdiag(Δfs))Σ(Ψ+Fdiag(Δfd)+Gdiag(Δfs))H}= (Δfd)TP1Δfd-2V1Δfd+(Δfs)TP2Δfs-2V2Δfs+C (41) 式中:C為常數。 P1= (42) P2= (43) V1= (44) V2= (45) 最小化式(41)可得到Δfd和Δfs的估計值 2V1Δfd+(Δfs)TP2Δfs-2V2Δfs} (46) 式(46)分別對Δfd和Δfs的偏導數為零,則可以得到字典失配誤差的更新,即 (47) (48) 通過式(21)獲得字典失配誤差補償后的空時導向矢量字典Φ(Δfd,Δfs),并重復迭代λ、λ0、Δfd和Δfs的EM估計過程直至達到設置的估計精度。在兼顧超參數估計精度和迭代收斂速度的情況下,設置超參數誤差預設值最大值1×10-3,最大迭代次數2 000次。 迭代完成后獲得稀疏解A及字典失配誤差,進而獲得修正后的空時導向矢量字典Φ,并重構雜波協方差矩陣,即 (49) 通過式(49)獲得CCM估計值后,雜波空時譜可以表示為 (50) 綜上所述,字典失配情況下的稀疏貝葉斯學習雜波空時譜估計方法具體步驟如下: 步驟1根據式(12)初始化空時導向矢量字典Ψ。 步驟2根據式(21)構建失配字典動態模型。 根據式(36)和式(37)計算均值μk和方差Σ。 根據式(39)、式(40)、式(47)和式(48)更新超參數λ、λ0、Δfd和Δfs。 判斷誤差是否達到預設值或迭代次數是否達到最大值,不滿足則重復步驟2。 步驟3根據式(49)估計雜波協方差矩陣,然后根據式(50)計算雜波空時譜。 為了驗證本文方法的有效性,通過如下參數生成仿真數據。雷達工作頻率fo=450 MHz,載機平臺高度H=9 000 m,陣元數M=8,相干脈沖數N=8,脈沖重復頻率fr=300 Hz,360個雜波單元在0°~180°均勻分布,雜噪比CNR=40 dB, 從距離R0=15 km處開始仿真3個距離單元的雜波數據,距離分辨率為37.5 m。實驗對比了本文方法和使用固定離散字典稀疏貝葉斯學習的SBL-STAP方法[18]。SBL-STAP方法中最大迭代次數為1 000次,正則化參數初始值取1×10-2,超參數修剪閾值取1×10-4。 實驗1為了比較不同偏航角情況(有無字典失配問題)對稀疏恢復STAP的影響,陣列采用正側視模式。折疊系數β=1,即雜波脊的斜率為1,對應載機運動速度vp=50 m/s。空時導向矢量字典網格劃分系數ρs=ρd=4,即歸一化空間頻率和歸一化多普勒頻率都被等間隔分為32份,這時雜波脊正好落在空時導向矢量字典網格點上,不存在字典失配的問題。圖3為真實雜波譜及上述兩種方法使用相同的3個雜波樣本進行稀疏恢復得到的雜波譜,可以看出當不存在字典失配時,SBL-STAP方法和本文方法形成的雜波譜均集中在雜波脊上,無明顯展寬,具有較好的雜波抑制性能。 圖3 不存在字典失配問題時的雜波譜估計 實驗2陣列采用正側視模式,折疊系數為β=0.8,即雜波脊的斜率為0.8,對應載機運動速度vp=40 m/s。空時導向矢量字典網格仍為實驗1中ρs=ρd=4的等間隔劃分,由于雜波脊斜率與字典網格不匹配,雜波脊不能完全落在空時導向矢量字典網格上,此時存在字典失配問題,如圖4(a)所示。從圖4(b)中可以看出, SBL-STAP方法恢復的雜波譜有明顯的展寬,分辨率不高,雜波抑制性能損失較大。由實驗1和實驗2的結果對比可以看出,這種雜波譜展寬的情況主要是由空時導向矢量字典失配造成的,說明字典網格失配會使得稀疏恢復性能明顯下降,STAP處理效果較差。而本文提出的基于動態字典的稀疏貝葉斯學習空時自適應處理方法,利用動態字典實現字典失配誤差的估計補償,能夠形成較為清晰的雜波脊、連續性和展寬情況都獲得了比較理想的結果,如圖4(c)所示。 圖4 存在字典失配問題時的雜波譜估計(正側視陣,β=0.8) 實驗3陣列采用非正側視陣,φ=30°,載機運動速度vp=50 m/s真實雜波如圖5(a)所示。從圖5(b)可以看出SBL-STAP方法恢復得到的雜波譜中雜波脊較實驗2中情況更為模糊,這主要是由于非正側視陣的雜波脊為橢圓形,存在更多不能落在空時平面網格點上的雜波單元,由于字典失配問題的影響,稀疏恢復得到的雜波譜誤差較大。而如圖5(c)所示,本文方法獲得的雜波譜仍然能夠形成較為清晰的雜波脊,在非正側視陣存在字典失配的情況下較SBL-STAP方法有較大的優勢。 除上述雜波譜恢復情況分析外,STAP處理的雜波抑制效果通常使用信雜噪比損失(Signal to Clutter plus Noise Ratio Loss, SCNRLoss)來衡量[26],即 (51) 式中: (52) 圖6為進行100次Monte Carlo實驗得到的平均結果。其中圖6(a)為正側視陣情況,折疊系數β=0.8存在字典失配情況下的信雜噪比損失。圖中OPT對應曲線表示利用CCM真實值進行STAP處理獲得的信雜噪比損失,稱為最優情況。可以看出本文方法形成了較窄的零陷,在抑制雜波的同時,能夠獲得較好的運動目標檢測性能,除了在主雜波區形成零陷外,其他區域的SCNRLoss均較小,僅比最優情況低2 dB左右。而SBL-STAP方法形成的零陷較寬,這會使得更多與雜波多普勒頻率接近的運動目標被當作雜波抑制掉,大大降低系統的運動目標檢測性能。圖6(b)為非正側視陣,φ=30°存在字典失配的情況下的信雜噪比損失。可以看到與圖6(a)相似的結果,本文方法主雜波區形成較窄的零陷,在抑制雜波的同時,能夠獲得較好的運動目標檢測性能。而使用固定離散字典的SBL-STAP方法形成的雜波抑制區域較寬,對于運動目標的檢測性能下降較為嚴重。 圖6 字典失配情況下的信雜噪比損失 稀疏恢復STAP方法受字典失配影響較大,雜波抑制性能下降明顯。本文提出了一種利用空時二維動態字典對失配字典誤差進行估計補償的稀疏貝葉斯學習空時譜估計算法,實現了存在字典失配情況下的雜波譜有效恢復,能夠有效提高機載雷達雜波抑制性能。仿真實驗表明,本文方法在存在字典失配的情況下,可以有效恢復雜波協方差矩陣,提高雜波抑制效果,其性能優于固定離散字典的SBL-STAP方法。1 信號模型
2 空時功率譜稀疏恢復及字典失配問題
2.1 空時功率譜稀疏恢復


2.2 字典失配問題

3 字典失配情況下稀疏貝葉斯學習空時譜估計
3.1 空時二維動態字典模型
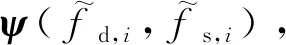

3.2 字典失配誤差估計及空時譜稀疏恢復
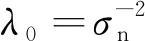
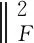

4 仿真實驗
4.1 雜波空時功率譜恢復效果比較

4.2 雜波抑制性能比較
5 結 論

