航空電子微距太赫茲互連DRR訪問容量分析
李峭,李佳,熊華鋼,楊勁赫
北京航空航天大學 電子信息工程學院,北京 100191
航空電子系統經歷了分立式、聯合式、綜合式和先進綜合式的發展歷程[1],目前正在發展分布式綜合模塊化航電(DIMA)架構[2]。現有的航電模塊或設備之間采用AFDX、TTE等綜合化網絡有線互連,設備內部采用ARINC659總線或從商用標準擴展而來的總線技術進行有線互連。
隨著微電子技術的進步,航電設備的體積、重量和功耗得以降低,逐漸出現了幾百克的綜合化處理機、板級或芯片級的互連接口[3];航電工程師發現,機載設備之間的電纜、光纜和緊固件也會帶來額外的空重和高昂的維護檢測成本[4],發展無線航空電子機內互連(Wireless Avionics Intra-Communication, WAIC)技術[5],用無線通信替代部分有線數據傳輸,已經得到國內外航空航天界的重視[6]。
對于機艙內相距米級乃至十幾米的航電設備之間的互連,國際電信聯盟(ITU)發布了WAIC的需求特性[7];NASA Langley實驗中心的電磁環境效應實驗室也在調研飛機內部全無線網絡化互連的潛在解決方案[6];學術界與工業界則嘗試將Wi-Fi(IEEE 802.11)技術[8]、5G移動通信技術[9]移植到機艙內部,并進行了信道仿真建模[10]和電磁兼容測試[11]等工作,并應考慮必要的屏蔽[12]。
在集成度很高的航電設備內部,空間尺寸以厘米度量,高密度的有線接插件和焊盤對裝配工藝提出巨大挑戰;采用無線互連則可以較好地解決航電互連“最后一厘米”[13]問題。這種處理板之間以及芯片之間的厘米級互連被稱為“微距”。太赫茲頻段[14]與既有航電設備的頻譜幾乎無沖突,在航空電子微距互連中體現出優越性[15];而且太赫茲信號的天線尺寸微小,可以與信息處理邏輯集成同一塊半導體芯片中,使芯片成為無線節點。
高集成度的太赫茲器件一般采用特殊的半導體工藝,如GaAs、InP材料;但也有通過巧妙的設計避免寄生損耗,獲得與CMOS工藝兼容的低成本方案[16-17]。
在太赫茲通信物理層模型方面,研究人員提出了適用于室內、室外和微距的信道的多種模型[18-19];出現了相應數字調制、多路復用、波束操縱的方法與器件[20-22];其中,技術門檻相對較低的是基于脈沖或脈沖串的鍵控通信,及其肖特基勢壘二極管非相干檢波接收[23-24]。
可以將幾個無線節點組成“簇”,在數據鏈路層協議的支持下,實現簇頭節點與簇內其他節點 “一對多”訪問。
太赫茲通信的數據鏈路層設計源于無線個域網(WPAN)[25]或微納網[18]。文獻[26]介紹了太赫茲介質訪問控制(Media Access Control,MAC)子層協議,它們被分類為中心、分簇和分布式控制。具體到航空電子微距互連,由于航電組件不可能像數據中心那樣規則地圍聚在一起,也暫時不存在動態組網需求,適宜層次化的分簇控制,利用簇頭節點進行簇內節點多路訪問。
太赫茲多路復用的方式包括TDMA(時分多路訪問)、輪詢(round-robin,RR)、CSMA/CA(載波偵聽多路訪問/沖突避免),以及使不同節點采用不同重復周期進行脈沖無線電通信的“速率分”(Rate Division,RD)體制[27]。航電互連需要在給定的時延和可靠性條件下保證一點到多點的實時消息傳輸[2,28],CSMA/CA或RD方式含有重傳或握手,很難滿足航電互連的性能要求。與之不同,TDMA和RR方式具有時間確定性,前者根據先驗的時刻調度表訪問;后者可以采用接收端發起的協議,適應未來太赫茲通信潛在的大容量高速率應用。
本文研究的航電微距互連采用簇頭到簇內節點TDMA訪問,以及簇頭對于簇內節點進行赤字輪詢(Deficit Round Robin,DRR)[29]的訪問方式。
安全關鍵性系統的驗證方法是理論分析或實驗測試[28]。對于航電互連訪問,需要驗證最壞情況下的性能,而不是平均性能;因而很難在較短時間觀測到最壞情況,只能采用理論分析方法,可以采用隨機網絡演算(Stochastic Network Calculus, SNC)[2]分析概率保證意義下的延遲界限。
如果要求航電系統具有超高可靠性,則失效率不能大于10-9次/小時[28];但這是容錯設計后的結果,并不意味著各個組件的可靠性指標都如此嚴苛,組件的瞬態故障率一般為10-3~10-6量級[28]。在SNC分析中,將超過延遲界限的“危害”(hazard)概率設為10-6,可滿足稀有概率條件,且與現有航電系統容錯能力相適應。
本文的主要貢獻在于:在充分考慮太赫茲開關鍵控(On-Off Keying,OOK)調制和非相干解調物理層誤碼率性能的基礎上,提出基于DRR的多路訪問和TDMA多播相結合的訪問控制協議,運用服務曲線模型和SNC方法對DRR訪問的時間確定性進行分析,推導出信道阻塞干擾模型下的有效容量。另外,還在物理層設計中考慮了同步精度對于報文長度、波束角度的影響。
1 航空電子微距太赫茲互連系統設計
太赫茲通信的優越性在于:① 太赫茲無線信號適于采用定向天線,其指向能力比GHz的電磁波強,但又不是像激光那樣的針狀波束,不需要復雜的對準裝置;② 太赫茲信號隨傳播距離增大迅速衰減,屬于不同簇的節點如果空間上相距稍遠,使波束彼此不交疊,可以復用時隙和頻道。
這樣,如圖1所示,在航空電子微距太赫茲互連應用中,采用與CMOS兼容的工藝構造太赫茲振蕩器,通過數字信息控制對振蕩信號進行鍵控;在接收端避免復雜的信號處理,采用肖特基二極管進行非相干包絡檢波。
為使下文的論述具有針對性,先對物理層和鏈路層的最基本實現方式加以限定。
1) 頻段的選擇
在太赫茲的低頻端,沒有明顯分子吸收峰的頻帶寬達0.1~0.54 THz[18]。
2) 天線的選擇
喇叭形天線具有好的指向性但不利于集成;超表面表征與數字編碼結合[21]依賴于反射型天線陣列,功率損失較大;石墨烯材料制造的大規模MIMO陣列[15]能夠獲得空間分集增益和自由度增益,但太赫茲信號處理具有難度。
為了避免復雜的信號處理,采用易于芯片內集成的定向天線,如領結形狀的天線,以半功率矢徑所夾的區域作為主瓣。
3) 介質訪問控制方式的選擇
對于航空電子微距太赫茲互連,應采用輕量化的協議保證訪問的時間確定性。采用分簇的網絡體系架構,每個簇具有確定的簇頭,簇頭節點具有信標功能,記為B,其他簇內節點稱為“用戶節點”,記為Ui,i=1,2,…,K,K為用戶數。
簇頭節點之間采用窄波束無線互連,或采用塑料波導互連;簇內互連距離則保持在厘米量級。在簇內,B和Ui之間采用半雙工多路訪問通信。B到Ui為廣播信道通信,采用TDMA調度(如圖2(a)),而Ui到B為多路復用信道通信,根據B的“點名”采用DRR調度(如圖2 (b))。
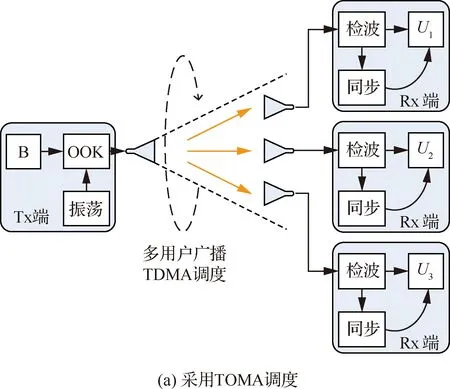
圖2 廣播信道與多路復用信道的介質訪問控制
2 太赫茲信號的OOK調制
2.1 無線電信道模型和天線增益
太赫茲互連的信道模型如圖3所示,乘性衰減為氣體分子吸收損耗Am和路徑損耗Ap,加性噪聲設為高斯白噪聲n,另外還要考慮信道衰落:作為隨機變量的信道增益h,以及阻塞式干擾J。將頻率記為f,則波長λ=f/c,c為光速;并設收發天線之間的距離為d。

圖3 太赫茲互連傳播信道模型
使太赫茲信號的頻譜避開明顯的分子吸收峰,并且不在水蒸氣飽和的環境下工作,對于距離不大于10 cm的通信,可以忽略分子吸收衰減,即令Am=1。
路徑損耗最簡單的模型為Friis公式,再考慮天線增益,路徑損耗為
(1)
式中:Gt和Gr分別為發射和接收天線的增益。
但在微距通信中,更簡易地是直接考慮天線間的幾何關系[20]。如圖4所示,設發射和接收天線的等效口徑都為2ra,發射天線波束到軸線的夾角為φ,則路徑增益為
(2)
式中:gc為修正系數,用于補償真實天線的空間方向性增益與圖4模型的差異。如考慮3 dB波束內的最壞情況,可令gc=0.5。如果dtanφ?ra,則有近似關系:

圖4 微距天線之間的路徑損耗
(3)
2.2 調制方式的選擇
基于脈沖的調制方式有開關鍵控(OOK)、脈沖位置調制(PPM)、幅移鍵控(ASK)、二進制相移鍵控(BPSK),它們將時間軸分隔為符號周期Ts,脈沖持續時間為Tp[24],占空比Tp/Ts<<1。其中,OOK以符號周期內有脈沖(或脈沖串)表示“1”,此時脈沖幅度記為a1;反之,則表示“0”,脈沖幅度記為a0=0。
除此之外,還有高效的頻域差分相移鍵控(FD-DPSK)和多進制的差分脈沖位置調制(DPPM)。但前者需要“聲子—光”調制器(Acousto-Optic Modulator,AOM),很難與芯片集成;后者在發射脈沖之后立即進入下一個符號周期,節省了時間資源,但必須解決插入刪節錯誤的問題,工程復雜度高。
一些文獻(例如文獻[30])在平均功率相等的條件下比較ASK、OOK和PPM等調制方式的誤碼率,但除非是電池供電的設備,更有意義的是在峰值功率相同的條件下比較,就是設接收端收到的脈沖或脈沖串的最大能量相同。對于二進制調制,誤符號的計算需要考慮“0”和“1”時信號矢量的歐幾里得距離d0,1,設發“1”時單位脈沖或脈沖串能量為E1,且信源0、1等概出現,并設此時脈沖幅度為“單位1”,平均功率和峰值功率意義下的調制參數如表1所示。
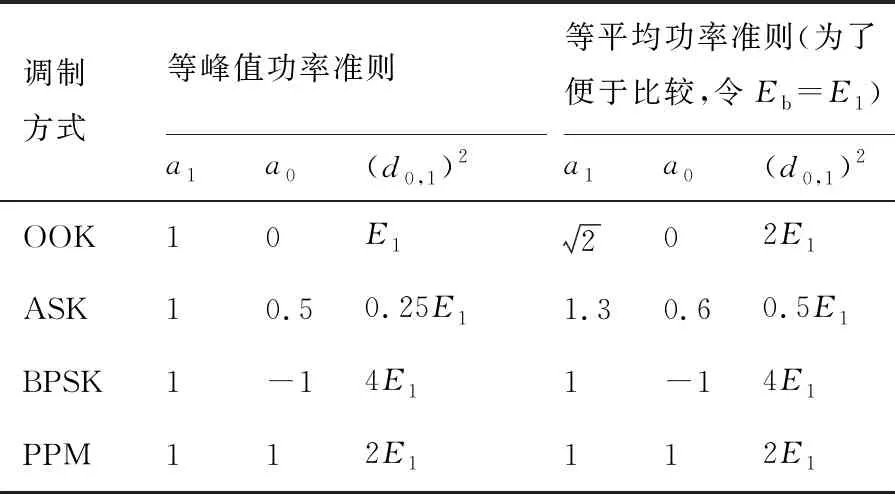
表1 幾種脈沖調制方式的參數
注:這里設ASK采用“1”信號的一半幅值發送“0”信號;PPM為二進制,且每個碼元含有兩個位置。
由表1可知,雖然BPSK性能優越,但很難識別太赫茲脈沖串的相位;表面上PPM指標很好,但浪費了兩倍的時間寬度。
因此,OOK是一種綜合性能很好的脈沖調制方式,且發送“0”的時候靜默,有利于緩解超寬帶信號的符號間串擾(ISI)。
如果接收端采用連續時間移動平均(CTMA)檢測[31],即在起始點和終止點可控的觀測窗內進行檢波(如圖5)。這是一種非相干檢測,不僅I、Q通道的噪聲都進入接收機,而且根據檢測理論,如果以a1/2為門限,平均每比特能量Eb=E1/2,OOK的“發0判1”和“發1判0”錯誤概率是不對稱的[32],前者概率小于后者。
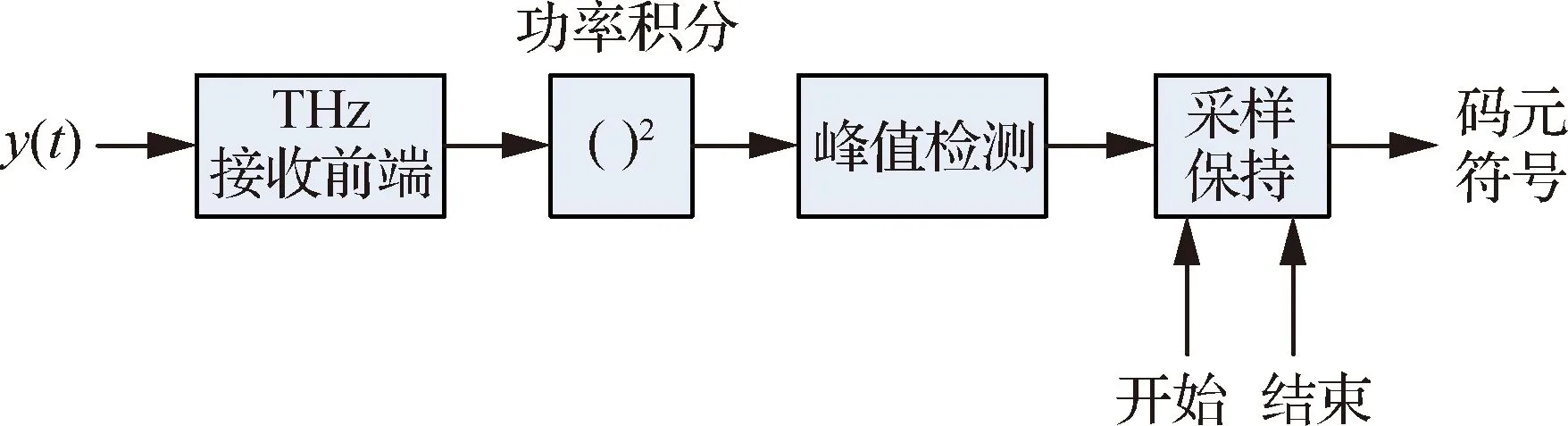
圖5 連續時間移動平均檢測器
(4)
(5)
傳統的OOK信號是一串以載頻fc振蕩的正弦信號,即
sOOK(t,m)=a·bm·s(t-m·Ts)·cos2πfc
(6)
式中:m為符號的序號;a為幅度;bm為數字序列對應的調制信息,即當“0”時bm=0,當“1”時bm=1;s(.)為符號的成形函數,定義域為 [0,Ts),但應使主要信號能量集中于Tp之內。
另一種開關鍵控的方式被稱為時間擴展開關鍵控(Time Spread OOK, TS-OOK)[24],采用飛秒級激光脈沖激勵諧開口諧振環等器件,生成極窄的電磁沖激,沖激在實際信道中展寬約100倍,成為能量集中于太赫茲頻段的高斯脈沖。
由于CMOS工藝的太赫茲振蕩器[13,17]產生固定頻率的振蕩,OOK信號采用式(6)定義的形式。
2.3 信噪比
接收端的加性噪聲有熱噪聲、散彈噪聲,以及分子吸收造成的閃爍噪聲[18]。由于受限于制造工藝,缺乏低成本的太赫茲信號放大器,超短距離太赫茲的接收端不采用有源放大,先只考慮熱噪聲,而將其他信道噪聲放到阻塞干擾模型中考慮。熱噪聲的功率譜密度為
N0≈Nth=kB·T
(7)
式中:kB為波爾茲曼常數,kB=1.380 650 5×10-23J/K,T為絕對溫度;如果取T=300 K,N0=4.142×10-21W/Hz。以下通過兩個算例進行展示。
例1發射峰值功率10 μW,發射、接收天線的等效半徑ra=0.5 mm,天線波束錐角60°(φ=π/6),距離d=3 mm;則根據式(2),路經損耗Ap=2 400。設Tp=10 ps,則Eb=0.04×10-18J(0.04阿焦),Eb/N0≈10,由式(4)和式(5),非相干解調誤碼率為10-2量級。
例2如果天線波束錐角30°,其他參數與例1相同,Eb/N0≈47,非相干解調誤碼率10-10量級。
可見,在太赫茲微距通信中,定向天線的設計非常重要。
2.4 時鐘誤差與數據包長度
太赫茲信號的占空比小,同步后才能合理控制取樣保持的位置。而且同步常用壓控延遲線電路迭代對準[31],每次需要前導信號,需要在考慮源、目的時鐘精度的條件下減小同步開銷。
設源和目的時鐘的精度誤差率為rclk,則經過m個符號周期Ts,考慮最壞情況,時鐘累積誤差為2m|rclk|Ts。為了在最壞的累積誤差情況下脈沖串仍能落在積分的時間窗之內,設計中要求后者的寬度比前者大一定的比率,被稱為容忍率rtol,即積分時間窗的寬度為 (1+rtol)Tp,則
(8)
例3|rclk|=10×10-6,rtol=10%,Tp/Ts=1%,則m=50,這種情況只能使用50比特的短幀通信。
應根據實際情況權衡選取rtol,因為提高容忍率會帶來信噪比的降低,反之則會造成幀長過短協議開銷過大[33]。
2.5 交織長度
為了對抗信道衰落(如:圖3中信道增益h的隨機性),單天線非相干解調方案只能利用時域上的交織。由于時間分集取決于信道波動的快慢,航空電子微距互連為固定安裝,相干時間很長,幾乎不存在時間分集,必須將信道編碼和交織結合。如果采用編譯碼比較簡單的線性分組碼,分集增益就是碼字間的最小漢明距離。
將待發送的比特串分成長度為Lb的分組,收集Nb個這樣的分組后,且取Nb=Lb,橫縱交織,編碼每分組加上長度為Mb的監督碼元。對于短幀,交織編碼可能跨越多個幀。交織和編碼在發送端和接收端造成固定的技術時延(Lb+Mb)2Ts。
3 微距太赫茲互連的DRR多路訪問
3.1 赤字輪詢多路訪問隊列調度
在多路訪問的隊列調度中,TDMA具有時間確定性,然而考慮到太赫茲通信潛在的大容量高速率應用場景,TDMA對于空閑隊列的等待造成時間資源浪費。采用DRR調度,可以在負載很重時保證一定的最壞情況下延遲,在輕載時維持動態的公平性。
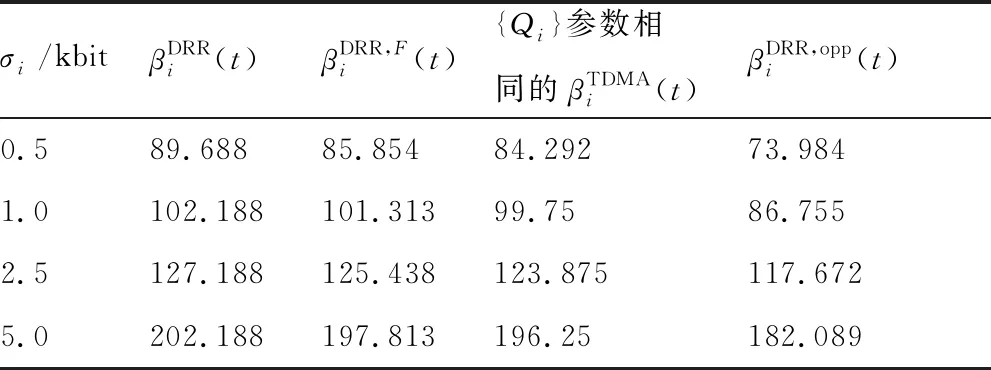
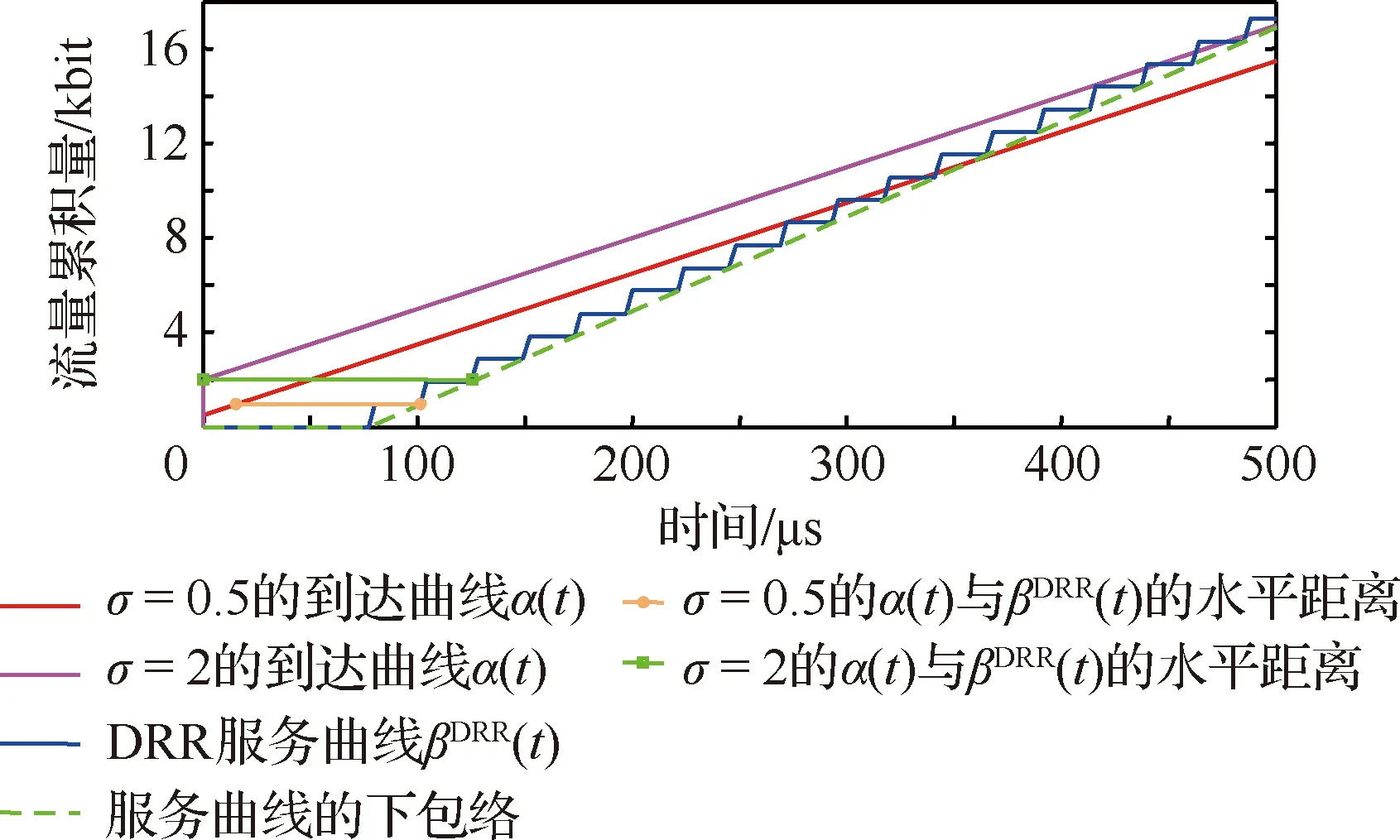
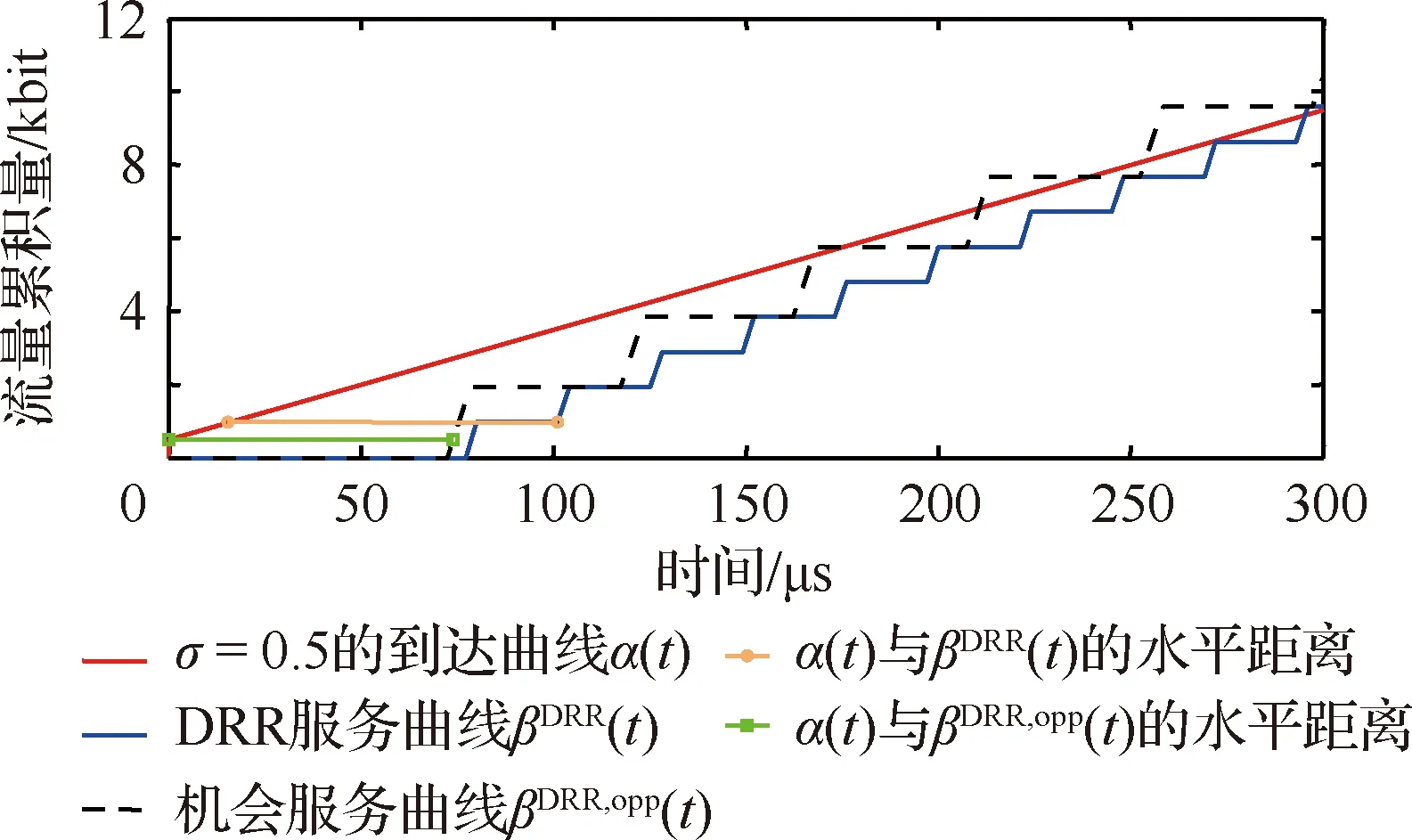
文獻[29]提出了DRR調度算法,步驟如圖6所示,每條隊列i被賦予一個信用量補充常數Qi,各自維護一個信用量計數值,記為qi,依次輪詢各個隊列,如果判決當時的qi不小于頭部數據包的長度li,則進行數據包發送,并減小的qi值;隨后,重復判決過程直至li=0(隊列為空)或qi 圖6 DRR調度算法流程圖 DRR調度中信用量計數器可以被分布式設置,即操作qi并不需要其它多路訪問節點的信息的,也不需要關心簇頭節點的輪次。在航空電子太赫茲微距通信中,設定采用半雙工,簇頭節點的TDMA發送時段Ti和DRR輪詢接收時段Di交替安置,如圖7所示,對于簇內節點i,簇頭結點發送結束之前發出本輪開始信令Si,隨后進入接收狀態;簇內節點i發送數據包的同時減少qi,結束時發出結束信令Ei通知簇頭。 圖7 簇頭和簇內節點的半雙工通信 這是一種完全分布式的控制,由接收方簇頭節點發起,但發送結點自主計算qi值,根據排隊情況和信用量計數器自主決定停止。實用上,當簇頭節點發現Ti時段有空余,可以發送Si使輪詢提前開始,且不影響剩余節點DRR協議的執行。 航空電子系統安全關鍵性的評價與認證需要最壞情況下時間確定性分析,網絡演算[34]就是最壞情況下排隊性能分析方法的一種。最早發展[35]的是確定性網絡演算,定義到達曲線α(t)、服務曲線β(t)分別作為突發流量的上界和傳輸服務的下界。 設流量R(t),如果存在廣義增函數α(t),稱R(t)受到到達曲線的約束,即對于任意時刻s≤t: R(t)-R(s)≤α(t-s) (9) 將MAC層控制機制抽象為服務器,設輸入流量為R(t),輸出流量為R′(t),廣義增函數β(t),設服務器最壞情況下提供的服務不小于β(t): (10) 受到α(t)約束的流量經過受到β(t)約束的服務器,最壞情況下的等待延遲為到達曲線和服務曲線之間的最大水平距離(如圖8)。 圖8 最壞情況下的延遲計算 針對DRR調度算法,文獻[36]采用網絡演算方法求得隊列等待時間的保守性上限,給出了通用形式的DRR服務曲線表達式: (11) 如果航空電子太赫茲微距通信采用半雙工模式,可以將廣播階段認為是Qi=Ti且lmax,i=Ti的DRR輪詢時段。 不同于具有固定信道參數的有線網絡,太赫茲無線信號會受到閃爍噪聲、氣體分子變化等復雜影響,而造成突發的深度衰落,可以將它們抽象為阻塞式干擾,如圖3所示記為J,進而需要在保證概率(guaranteed probability)意義下研究實時通信的性能。 與保證概率互補的是“危害”(hazard)概率,不受性能保證的危害事件是稀有事件,具有非漸近的統計規律,不宜采用常規排隊論,而要采用大偏離原理(Large Deviation Principle,LDP)[37]。Cramer定理和通信中應用的Chernoff界就是LDP的早期成果。為了更方便地表達保證概率下服務器的性能,文獻[38]提出了有效容量(effective capacity)的概念。設MS(-θ,t)為服務過程S(t)在參數為-θ下的矩生成函數(Moment Generation Function,MGF),θ≥0,則有效容量定義為 ρS(θ)=ln[MS(-θ,t)/(-θt)] (12) 這種研究方法是用一類仿射的“速率—時延”服務曲線βS作為服務過程S(t)的包絡[39],其表達式為 βS=ρS·(t-τ)+ (13) 在圖9中,-b為帶有斜率的射線延長線到縱軸的截距,b表示對于累積量突發的容忍能力,有 圖9 保證概率意義下的服務包絡 b=τ·ρS (14) 根據Chernoff界,“危害”被概率量化為 Pr{S(t-s)<ρS·(t-s)-b}≤ε(b) (15) 式中:ε(b)為赤字輪廓(deficit profile),它隨著(-θ·b)指數衰減,一般定義為 ε(b)=αS·e-θ·b=eθ·σS·e-θ·b (16) 式中:由于LDP只能給出在指數意義上的度量,αS為選定的經驗常數,或將它轉變為指數并用θ歸一化,記為σS,可以看作概率保證的裕量。 如果考察樣本路徑包絡的赤字輪廓[39],會比式(16)的定義更加嚴苛,所以演算中要充分考慮到裕量的設計。 對于阻塞式干擾,如果很難描述其內在的機理,可以采用有限狀態馬爾科夫模型描述其外部特點,其參數可以通過測試實驗或經驗數據得到。例如:如圖10所示的簡化的兩狀態離散時間馬爾科夫模型[40],包含兩個狀態:狀態1為“好”狀態,狀態2為“阻塞”狀態,狀態的一步轉移概率為p11=1-p、p12=p、p21=r和p22=1-r。該模型也與描述突發的Gilbert-Eiliott模型(以下簡稱“G-E”模型)類似[41];則由文獻[40],保證概率下的速率為 圖10 簡化兩狀態離散馬爾科夫模型 (17) 式中:R為“好”狀態時的速率。 設系統設計要求“危害”概率不能大于ε,將與之相對應的θ值記為θ*,根據式(14)和式(16),有 θ*=(-lnε+σS)/(ρSτ) (18) 為了書寫方便,令 η=(-lnε+σS)/τ (19) 將式(18)代入式(17),解關于ρS的方程,得到 (20) 如果阻塞式干擾變化較快(如:閃爍噪聲),突發時間τ較短,η遠大于r和p,則ρS接近R;但如果τ很長,則ρS接近G-E模型中速率的均值,即 ρS(θ*)≈ρS(0)=r/(r+p) (21) 在一定的保證概率要求下,簇頭節點的服務曲線為 β(t)=ρS·(t-τ)+ (22) 2) 若ρS·τ與鏈路層累積量突發相比較小,可以將物理層和鏈路層的累積量突發合并,即 (23) 式中:bi=λiτ+Qi(L-lmax,i)/F+(F-Qi)(Qi+lmax,i)/F,λi=Qi·ρS/F;Qi,F,lmax,i的定義參見式(11)。 這樣,隊列i最壞情況下接受服務的等待時間τi體現了DRR調度器與理想調度器的差距,為 τi=τ+vi+wi (24) 式中:vi=(L-lmax,i)/ρS,wi=(Qi+lmax,i)·(F-Qi)/(Qi·ρS)。 設采用例2所示的物理層參數,且設符號周期Ts=1 ns,即物理層無編碼速率C=1 Gb/s。如果采用(7,3)循環碼,交織后每半個字節具有3個監督碼元,為了符合第2.4節的短幀原則,第7個7比特分組再加上1個符號間隔共50個符號,考慮編碼開銷后R=0.56C=560 Mb/s。 例2中非相干解調的誤碼率在10-10量級,遠高于保證概率要求,所以,以此速率R作為未考慮阻塞干擾前的物理鏈路速率 1) 阻塞概率對于保證概率服務速率的影響 例4設τ=10 μs,“危害”概率為ε=10-6,考慮裕量αS=10,則由式(13),b=5.6 kbit。 對于例4中保證概率的要求,設一步阻塞概率p=1 (μs)-1,對于一步恢復概率r的不同取值(如表2),由式(17)得到η,并由式(18)分別計算出ρS(θ*)。在上述參數設定下,圖11繪制了ρS(θ*)隨r變化的趨勢。注意橫坐標用η對r歸一化,1/η具有保證概率下突發時間的含義;r/η較小時,說明突發時間段內阻塞效應不劇烈,ρS(θ*)/ρS(0)(圖中虛線)較大,保證概率意義下有效容量大于G-E模型均值速率;反之,當r和p成為主導因素,有效容量的增長趨緩(圖中實線ρS(θ*)/R)。 2) 突發時間對于保證概率服務速率的影響 例5設“危害”概率ε=10-6,裕量αS=10,阻塞模型中給定p=1 (μs)-1,r=0.1 (μs)-1,如表3,研究不同尺度的τ對于ρS(θ*)的影響。 表3 突發時間與有效容量 可見,不論對于減小網絡演算下的最壞情況下時延還是增加有效容量,較短的τ都有優勢。然而,突發時間反映的是作為保證概率下包絡的仿射服務曲線對于信道不穩定的容忍程度,該參數不是隨意選定的,而是要根據實際工況設定。 如果阻塞干擾嚴重影響了系統穩定(即:p較大),τ的取值應與p-1+r-1的量級類似。 3) 考慮輸入流量到達模型的延遲計算 多路訪問的延遲界限需要在同時考慮輸入流量的到達曲線和服務器的服務曲線。 例6設共有4個簇內節點(n=4,i=1,2,3,4),物理層參數同例2,Ts=1 ns,保證概率參數同例4;設計選取τ=10 μs且ρS=60%×R≈320 Mb/s,設簇頭廣播時每時隙長Ti=3 μs。為了便于書寫,采用給定Ts下的傳輸時間作為數據長度單位,多路接收時每時隙長Qi=3 μs,數據包長0.05 ns;對于隊列i的輸入流量速率設為ρi=30 Mb/s,考慮輸入突發度σi與交織長度有關,分別為300 bit、500 bit、1 kb和5 kb下計算DRR隊列的最壞情況下延遲。 如果更精細,可以體現的Qi的作用,并使DRR服務曲線以周期F延拓,得到 (25) 式中:Δi=τi-(F-Qi)。 對于到達流量,由于每個數據幀很短,可以采用流體模型[34],設突發度為σi,可持續流量為ρi,有 αi(t)=σi+ρi·t (26) di=τi+(F/Qi)·(σi/ρS) (27) 表4給出了不同到達突發度下網絡演算的結果,利用RTC工具箱[42],圖12展示通過到達和服務曲線之間水平最大距離求延遲上界的原理。 表4 不同服務曲線下的延遲界限 圖12 根據到達曲線和服務曲線求延遲上界 然而,DRR多路訪問具有TDMA無法比擬的靈活性,當部分DRR隊列空閑,它們的剩余服務能力就會被其他有積壓的隊列動態按比例分享。 (28) 圖13展示了這樣的“機會性”會帶來最壞情況下延遲的改善,更進一步,如果n足夠大,還可以利用大偏離原理中的Cramer定理進行保證概率分析[37]。 圖13 機會服務曲線與常規服務曲線的對比 作為一種超寬帶大容量的通信技術,太赫茲的物理層和鏈路層的設計參數必須綜合考慮,具體結論為 1) 數字通信體制決定了比特誤碼率與Eb/N0的關系,進而決定了物理鏈路的可達速率;同步操作的精度決定了數據包長度的上限。 2) 與TDMA方式相比,DRR隊列中的數據包的最壞情況下接受服務的等待時間略大,但具有多路訪問的靈活性,且便于分布式實現,適于簇內用戶節點到簇頭的多路訪問。 3) 信道阻塞深度衰落的概率決定了最壞條件下的通信服務能力,通過對阻塞干擾建立兩狀態馬爾科夫模型,并與DRR服務曲線模型相結合,利用SNC方法得到保證概率下的有效容量。 在案例研究中,點到點互連保證概率下有效帶寬為320 Mb/s,但對于Gb/s量級的芯片間互連需求,如雷達成像、未壓縮視頻等[1],仍需要挖掘太赫茲數字通信體制的潛力。 另外,尚待解決的問題為:在航空電子設備的金屬腔體內,缺乏豐富的散射體,多模反射“回聲”疊加造成信干噪比增加,擬通過三維射線仿真等方法建立更細致的信道模型。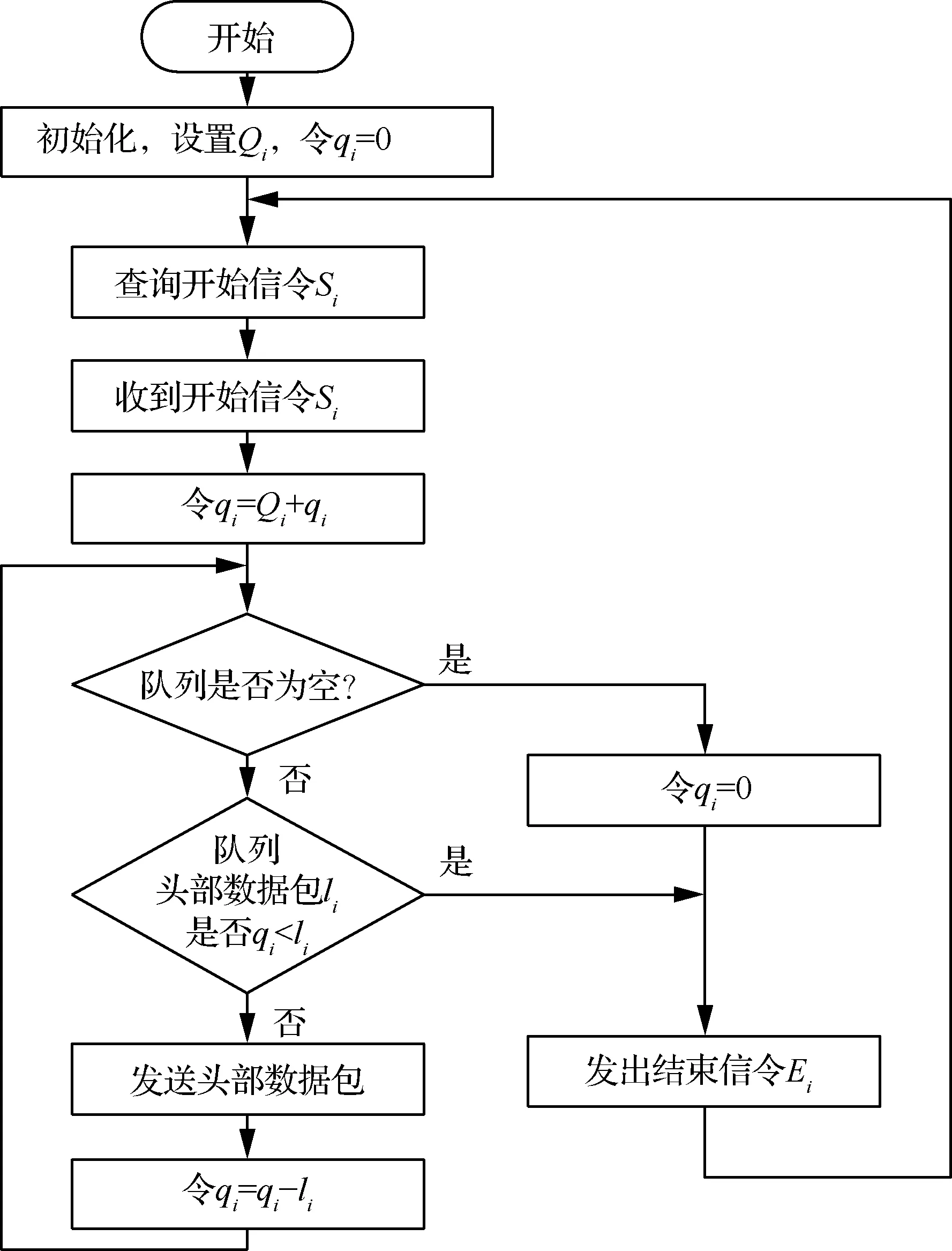
3.2 航空電子太赫茲微距通信中的DRR調度

3.3 DRR多路訪問的服務曲線
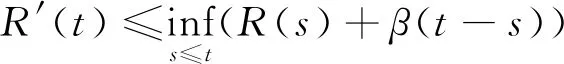

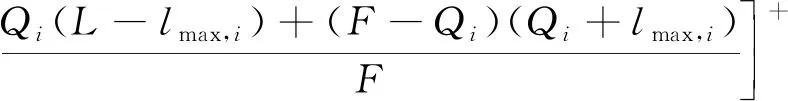

3.4 阻塞式干擾的隨機網絡演算


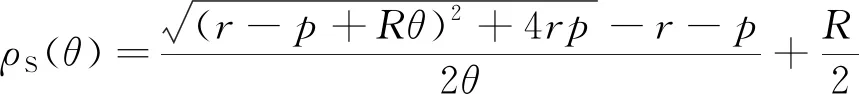
4 微距太赫茲互連的時間確定性分析
4.1 分析結果
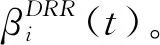

4.2 算例研究

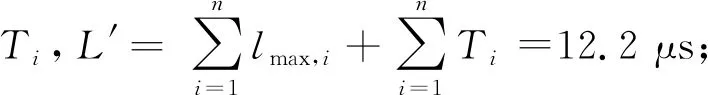
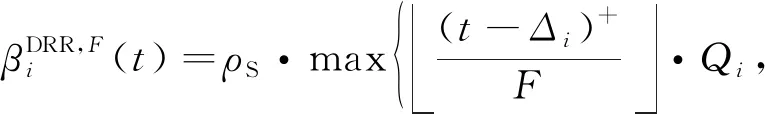
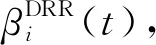
5 微距太赫茲互連多路訪問的靈活性

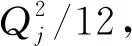

6 結 論

