分布式電推進飛機動力系統評估優化方法

雷濤，孔德林，王潤龍，李偉林，2，張曉斌，2

1. 西北工業大學 自動化學院，西安 710129

2. 飛機電推進技術工信部重點實驗室，西安 710129

隨著社會的不斷發展，飛機逐漸成為人們首選的出行方式，相應地，商業飛機每年的飛行時間與里程數大大增加，由此所帶來的化石燃料大量消耗、溫室氣體排放量增多、噪聲污染等問題引起了人們的廣泛關注[1-2]。

為了解決燃料過度消耗與環境污染問題，美國國家航空航天局(NASA)于2008年提出了未來20年飛機技術的發展目標。以目前的運輸客機技術指標作為基準，將噪音降低71分貝，氮氧化合物排放量降低80%，同時燃料消耗降低70%[3-4]。此外，國際民用航空組織(ICAO)也制定了飛機的發展目標。從2010年到2020年每年提高2%的燃料效率，從2020年開始實現碳中和增長，并將二氧化碳排放量減少50%[5]。為了實現ICAO和NASA提出的發展目標，必須對現有的飛機推進系統進行全方位的改進。

近年來，隨著電池、電力電子器件和電機效能的提高，人們開始重新關注使用電力作為飛機主動力的可行性。目前渦輪風扇發動機對燃料產生的化學能的利用率僅有40%左右，而電推進飛機系統對電能的利用率能達到70%[6]。顯然，采用電推進飛機系統可以明顯減少燃料消耗、噪音產生以及污染物的排放，因此飛機制造商正在研究探索多電飛機(MEA)、混合動力飛機(HEA)等系統來實現動力總成的電氣化。

多電飛機系統通過優化非設計點工作規范、消除引氣、電動增壓等方式提高了發動機性能，同時使用電氣系統取代液壓系統，在降低了設備重量的同時提高了二次能源和電能利用率。在多電飛機系統中，電池可用于提供負載和應急電源所需的瞬態功率。而在混合動力飛機系統中，電池還可以通過電動機的制動運行狀態獲得回饋能量。油電混合電推進飛機系統主要以發動機、蓄電池等儲能裝置和電動機作為飛機動力來源，具有高性能、低能耗和低污染的特點以及技術、經濟和環境友好等方面的綜合優勢。與傳統的發動機推進系統和純電動推進系統相比，油電混合電推進飛機系統中動力系統具有多種組合方式，并能夠根據飛行剖面對系統的工作方式做出優化組合，使作為主動力源的發動機能夠維持在經濟運行區和低排放區工作，以保證飛機良好的動力性、低排放性和低能耗性。雖然油電混合動力系統可以減少燃料消耗并改善對環境的影響，但同時也帶來了一些缺點，例如系統的復雜性更高，增加配電系統導致飛機整體的體積和質量增大，以及推進功率較高時電氣系統可能存在的可靠性等問題。

電推進飛機系統使用電能產生所需的動力，因此需要電能裝置提供足夠的推進功率，目前電推進飛機的推進功率等級從數十千瓦到幾十兆瓦不等[7]，根據推進功率的不同，動力系統所選用的架構也有所不同。小功率的電推進飛機主要被應用在無人機與短途飛行的商用單雙座飛機場合，在這種場景下，只使用電池作為推力來源的純電推進系統架構有著更大的優勢；對于兆瓦級電推進飛機，受限于電池的容量，需要采用渦輪發電機與電池組共同為飛機推進器提供能量來源。

目前電推進混合動力系統在汽車、船舶等方面應用較為廣泛，而對于飛機混合動力系統的研究起步則較晚，在充分吸取汽車、船舶領域的研究經驗后，目前國外航空領域也在逐步研究開發電推進飛機混合動力系統的概念設計工具，并提出了多種評估優化方法。

有學者采用一種為電氣系統各部件設定固定的效率來分析各部件的功率損失情況的方法來獲得電氣系統的功率損失[8-9]，盡管這種方法提供了快速的系統分析能力，但可能缺少對電力系統重要性能的評估。文獻[10]將地面交流電網中經常使用的功率流分析方法應用到電推進飛機系統的概念設計中，建立了電氣系統各部件的數學模型，并對一種渦輪電動傾斜翼飛機的配電系統進行了分析，得到配電系統在穩定運行狀態與斷路狀態下的電網電壓電流分布情況。雖然文獻[10]對電推進飛機配電系統進行了較為準確的分析，但是沒有與機械部件進行對接，不能夠對完整的動力系統進行分析。文獻[11]提出了一種基于功率/負載流建模的電推進飛機動力系統電氣部件建模仿真方法，該方法建立了電氣系統的準靜態模型，用來預測系統的穩態性能，以及控制系統的動態相應。這種電氣建模方案基于MATLAB/SIMULINK平臺，將電氣系統模型與用熱力學系統建模和分析工具箱(T-MATS)創建的發動機模型集成在一起，解決了創建電推進飛機動力系統的系統級模型時存在的兩大問題，如何保證電能傳輸的效率，以及電氣系統的動態如何影響非電氣部件。

如前文中所提到的，混合動力推進技術在汽車與船舶領域已經得到了廣泛的應用，因此也早已開發出了相關的建模與優化工具，例如用于評估混合動力汽車對環境產生的影響與汽車性能的軟件Advisor[12]與AVL Cruise[13]等，這些仿真工具對動力系統的每個部件采用統一的模型方法[14]，并采用后向仿真方法(假設已知駕駛條件，計算車輛的瞬時動力要求以滿足駕駛條件)對動力系統進行評估與優化。仿照這種建模方法，文獻[15]介紹了用于復雜飛機動力系統設計和優化的模擬方法，在此基礎上，文獻[16]基于多學科方法，綜合考慮了飛行力學、空氣動力學與熱力學等多種約束條件，建立了動力系統各部件尺寸與功率模型，開發出了用于評估傳統飛機和電推進飛機架構的性能、成本和環境影響的仿真軟件。文獻[17]在MATLAB環境下開發了一種用于確定電推進飛機動力系統架構尺寸的設計軟件，該軟件通過輸入電動機的需求轉速與轉矩，計算出動力系統各部件的物理尺寸與重量，以及系統的功率損失與效率，該軟件是基于STARC-ABL電推進飛機架構而設計的，沒有考慮進儲能裝置對動力系統的影響。

文獻[18]提出了一種針對電力電子變換器的重量優化設計方法，采用多種分層權重優化設計算法解決設計變量識別和設計交互解耦過程中的困難，具體包括諸如遺傳算法(GA)、粒子群優化(PSO)和模擬退火(SA)此類的元啟發式優化方法。文獻[19]介紹了符號規劃(SP)在電力推進系統評估和多學科優化中的應用，通過基于Python開發的GPKit軟件包提供的SP算法，對建立的電推進系統電氣部件和機械部件的尺寸和性能參數化模型進行了優化，并通過分析對比渦輪直接驅動架構、渦輪-電驅動架構與變速渦輪-電驅動架構的總重與效率，說明了電推進系統在器件級優化設計中質量和效率之間的權衡。

本文針對目前電推進飛機頂層設計手段匱乏、能量流動與耦合機理不夠明晰、關鍵部件的性能尺寸參數化模型缺乏積累的問題展開研究，以期為電推進飛機的設計與評估優化方法提供設計工具積累。

本文第1節介紹了潮流分析方法的基本概念，以及牛頓法的迭代計算流程，分析了電推進飛機電氣系統在正常運行與斷路故障情況下的電網狀態與母線電壓等級對電網的影響；第2節在SIMULINK環境下搭建了動力系統的仿真模型，同時設計了基于時間和基于高度的兩種飛行剖面，給出了渦輪電推進與純電推進架構的仿真分析結果；第3節建立了動力系統各部件的參數化優化模型，介紹了符號規劃優化算法的基本原理，并利用該優化算法對動力系統進行了優化分析，得到了相應的分析結果；最后在第4節對全文進行總結，并給出了結論。

1 電推進飛機電氣系統能流關系分析

潮流分析方法是一種獲得電力系統各種電源及負荷在穩定狀態下運行的參數的數值計算的方法。在電推進飛機系統中，發電機產生的電能是推進系統最主要的能量來源，對飛機電氣系統使用潮流分析方法，可以得到固定運行狀態下電網中的電壓與電流分布情況，對電推進飛機電氣系統的設計有著十分重要的意義。

1.1 潮流計算方法

1.1.1 數學模型

電力系統由發電機、負荷、輸電線等部分組成，在進行潮流計算時，通常會將發動機與負荷這些非線性部件用接在對應節點上的電流量表示，而將其他的線性部件組合成用于潮流計算的線性網絡。對于這種線性方程，一般采用節點法來得到節點電壓與電流之間的關系，表達式為

(1)

對第i個節點，其展開式為

(2)

式中：n為電力網絡總節點數。

通常在實際計算中，已知的數據為節點功率而非節點電流，因此，需要用節點功率來表示節點電流，得到節點功率與節點電壓的表達式為

(3)

對節點電壓向量用直角坐標形式可表示為

(4)

將導納矩陣用復變量表示為

Yij=Gij+jBij

(5)

將節點電壓向量的直角坐標表達式與導納矩陣代入式(3)中，并按實部與虛部分開計算結果，就可以得到如下潮流方程：

(6)

該潮流方程通常也稱為節點功率方程，是潮流算法最普遍采用的數學模型。

1.1.2 數值計算方法

用于潮流計算的數學模型是一組高階的非線性方程，為了求解這些方程必然要用到迭代運算的方法。由于電網系統規模的不斷擴大，用于潮流計算的方程組的階數也越來越高，甚至會達到上萬階，人工解算這些方程組顯然是不現實的，因此研究人員開始尋求利用數字計算機求解潮流問題。

最開始，受限于計算機內存與計算速度的限制，普遍采用的是以節點導納矩陣為基礎的高斯—賽德爾迭代法(導納法)和以阻抗矩陣為基礎的逐次代入法(阻抗法)[20]。導納法的收斂性較差，而阻抗法雖然改善了迭代算法的收斂性，但每次迭代的計算量較大，無法滿足大型系統的實時性要求。隨著計算機的不斷發展，牛頓—拉夫遜法(牛頓法)被廣泛用于潮流計算問題中，牛頓法的核心是將非線性方程線性化，并反復地對相應的線性方程進行求解。在使用牛頓法時，只要保證初始值設置合理，同時在迭代過程中使方程組的系數矩陣保持其稀疏性，就能以很快的速率解決潮流計算的問題。由于牛頓法具有很好的收斂性與運行速率，牛頓法成為了處理潮流計算問題最主要的方法。

牛頓法是大部分電力系統潮流計算方法的基礎，許多方法都是對其改進得到，因此，了解了牛頓法的迭代原理，對潮流計算問題也就有了相對透徹的了解。下面將簡單介紹牛頓法的計算步驟，整個計算方法的流程如圖1所示。

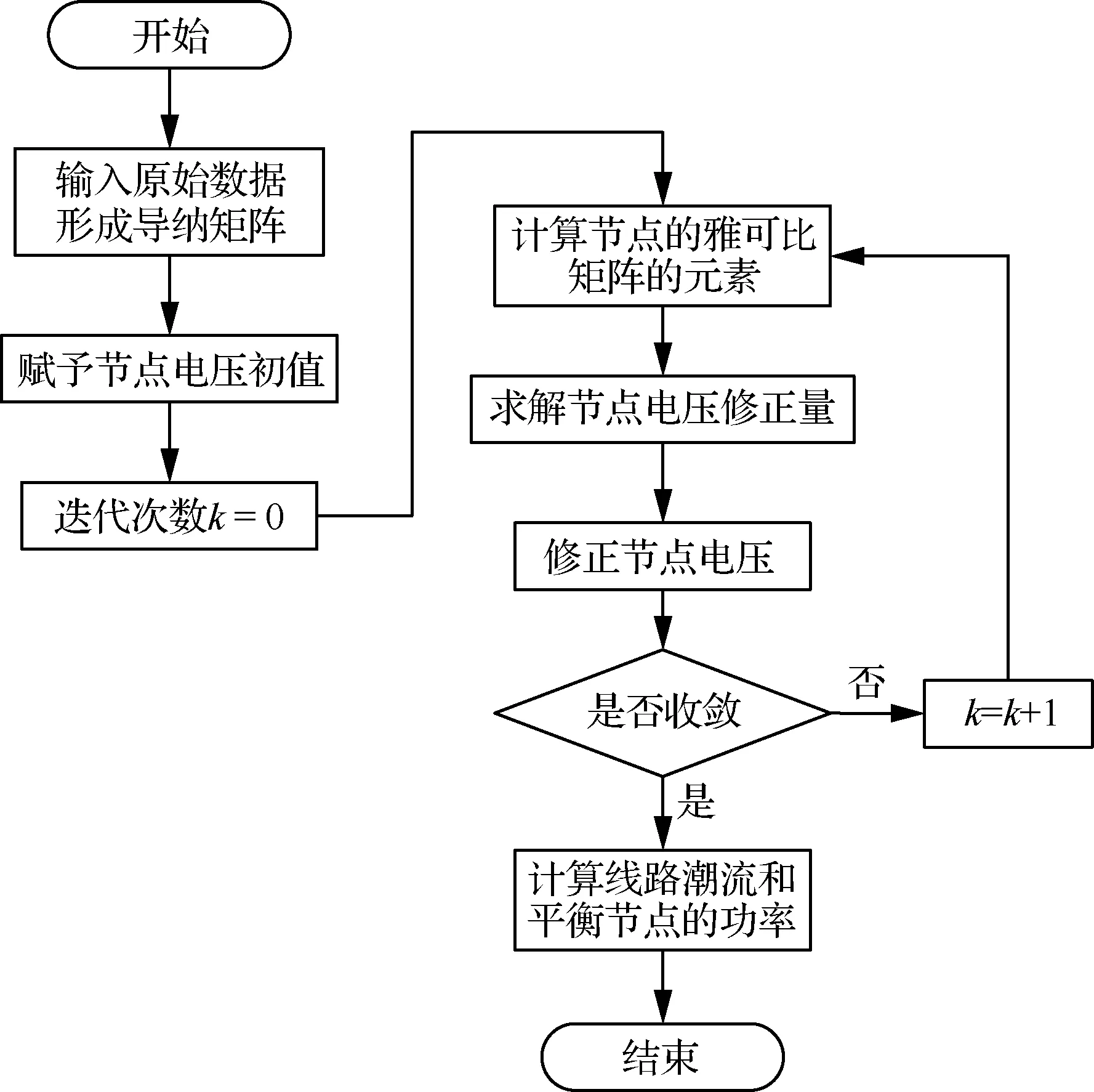
圖1 牛頓法潮流計算流程圖

1.2 潮流分析結果

1.2.1 配電架構選擇

電推進飛機電氣系統的能量傳輸架構多種多樣，其中最常見的有直流電力系統、混合交直流系統和交流系統。對于直流系統架構，由于功率傳輸需要從變頻交流發電系統，將電功率進行兩次傳輸，在電機和電力電子變換器之間是交流電，在配電和傳輸系統之間為直流功率，因此電力系統包含了整流器和逆變器，存在功率損耗和系統重量之間的優化約束，但是由于發動機不提供系統推力，因此可以使其運行在最佳工作點，減小發動機的燃油消耗。交流架構在發電機和電動機之間沒有電力電子變換器，因此功率損耗較小，但是其中需要將發動機輸出功率傳遞到推進電機上，需要增加機械傳動裝置，不方便儲能裝置接入到電氣系統中，也增加了系統對推力動態需求的不確定性。混合交直流系統中主要采用的是交流電，對應每一個電動機，采用背靠背變換器實現獨立速度優化，但是多個電力電子變換器的使用，增加了系統的效率損耗。

由于直流輸電系統能夠保證發動機運行在最佳工作點，不需要額外的機械傳動裝置，同時減少電氣系統的諧波污染與傳輸損耗，因此本文選擇對這種配電體制進行潮流分析，并且對整個系統選擇了分布式布局。采用這種設計方式的原因在于這種配電系統的潮流分析較為簡單，可以將該分析結果作為基準數據，為后續的配電系統設計提供對比依據。系統構型如圖2所示。

圖2所示的電能傳輸系統是針對翼身融合分布式渦輪-電推進飛機系統設計的，系統共包括2個渦輪發電機系統與8個推進單元，整個配電系統共分為2組，每組各由1個發電機和4個推進單元組成。在該系統中，渦輪發動機與頂端的交流發電機相連，交流發電機產生三相交流電壓傳輸到整流器，整流器將其轉換為直流電壓后，通過母線傳輸到逆變器，再由逆變器將直流電壓轉化為交流電壓，驅動電動機工作，最終產生機械功率輸送給推進器。

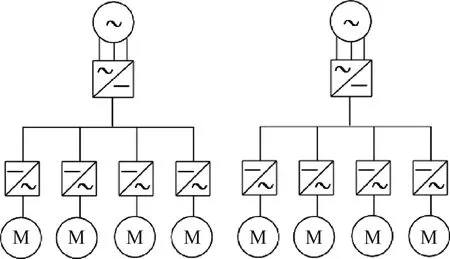
圖2 分布式電推進飛機高壓直流配電系統架構

由于兩組配電系統是完全對稱的，因此在接下來的分析中，只選取了其中一組進行分析。額定狀態下4臺電動機的有功與無功功率均設為相同，整流器與逆變器的參數統一用變換器表示，輸電線每米的電阻值設置為0.009 6 Ω，配電系統具體的參數值設定如表1所示。

表1 配電系統額定狀態參數值

1.2.2 穩定運行狀態分析結果

考慮到飛機飛行過程中的姿態轉換，穩定運行狀態共分為2種情況。第1種是電動機負載功率對稱分布，這種情況下飛機處于平飛狀態；第2種是電動機負載功率從左到右等間距增加，這種情況下飛機處于傾轉狀態。為了便于進行對比分析，假設這兩種情景下電動機負載提供的總功率不變，均為27.8 MW。出于系統安全冗余的考慮，推進部件中的逆變器母線之間通過輸電線互相連接。流過直流輸電線的電流以及直流母線電壓的大小由不同顏色表示，具體的分析結果分別如下所述。

1) 電動機負載功率對稱

在這種情況下，4臺電動機負載的有功功率均設為6.95 MW，如圖3所示，從分析結果中可以看出，由于中間位置的兩根直流輸電線的傳輸路徑短，電阻較小，所以流過這兩根輸電線的電流是最大的，其中，絕大部分電流通過逆變器為電動機負載傳輸能量，小部分電流輸送到了兩側的逆變器母線上。同時，由于電動機負載是對稱分布的，因此沒有電流流過連接中間2個逆變器的導線。

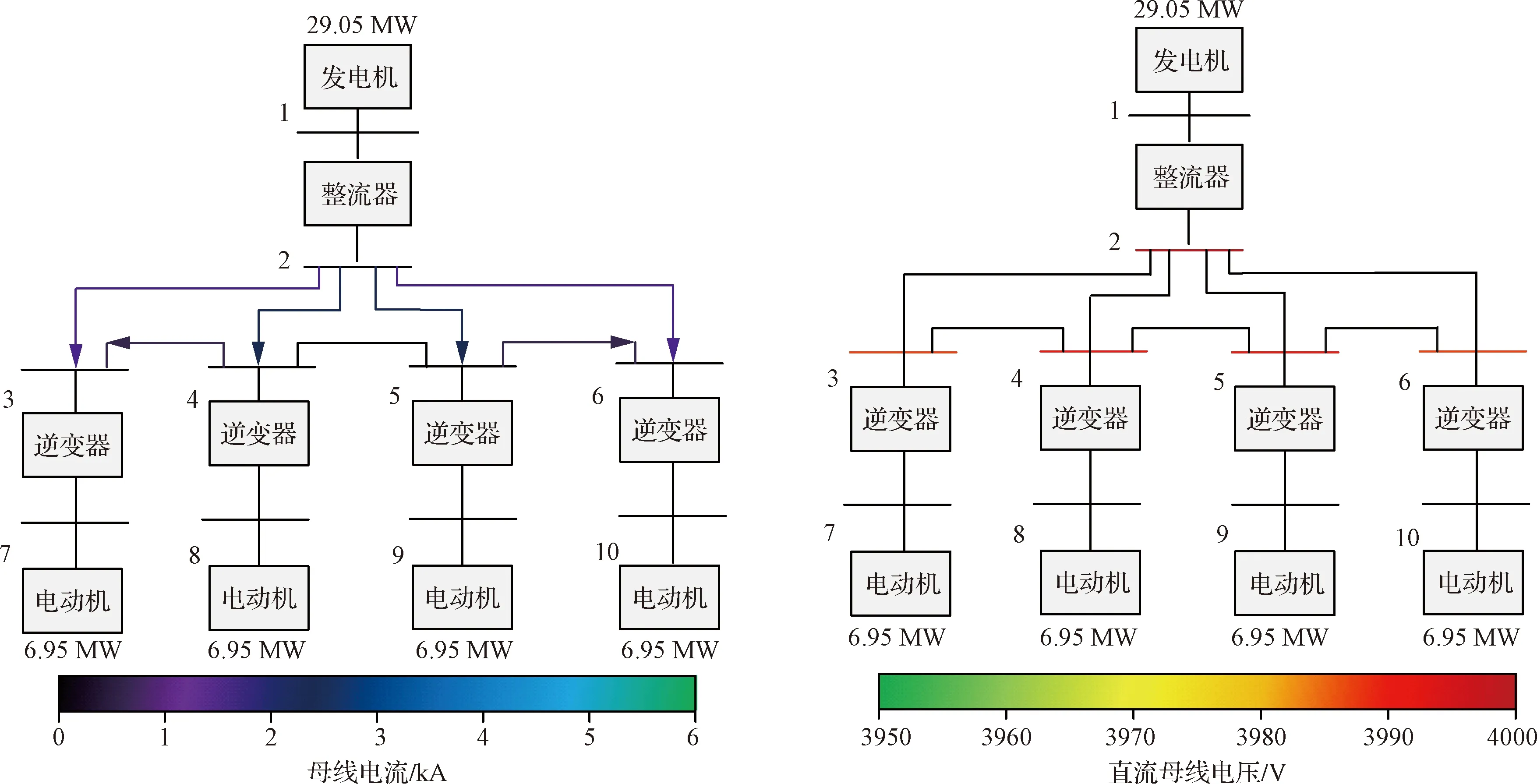
圖3 負載對稱穩定運行狀態

在母線電壓方面，直流母線2的電壓與設定值相同，穩定在4 000 V，靠近中間的母線4與5的電壓比兩端的母線3與6的電壓值稍微高出一些。

2) 電動機負載功率不對稱

在這種情況下，4臺發電機負載的功率按照0.1 MW的差值從左到右等間距增大，但電動機所提供的總功率仍然與負載功率對稱情況下的數值保持一致。如圖4所示，從分析結果中可以看出，直流輸電線上的電流呈現出“中間大，兩端小”的特點，雖然看上去直流輸電線上流過的電流與負載功率對稱情況下相同，實際上右側輸電線上的電流要比負載功率對稱情況下略大一些，這是因為右側的電動機負載的功率要比負載對稱情況下更大。同時，有少量的電流流過了連接中間兩個逆變器的輸電線。在母線電壓與發電機的有功功率方面，分析結果與電動機負載對稱情況下相差很小，說明在負載功率相差不大的情況下，母線電壓幾乎沒有波動，發電機所需提供的功率也沒有改變。

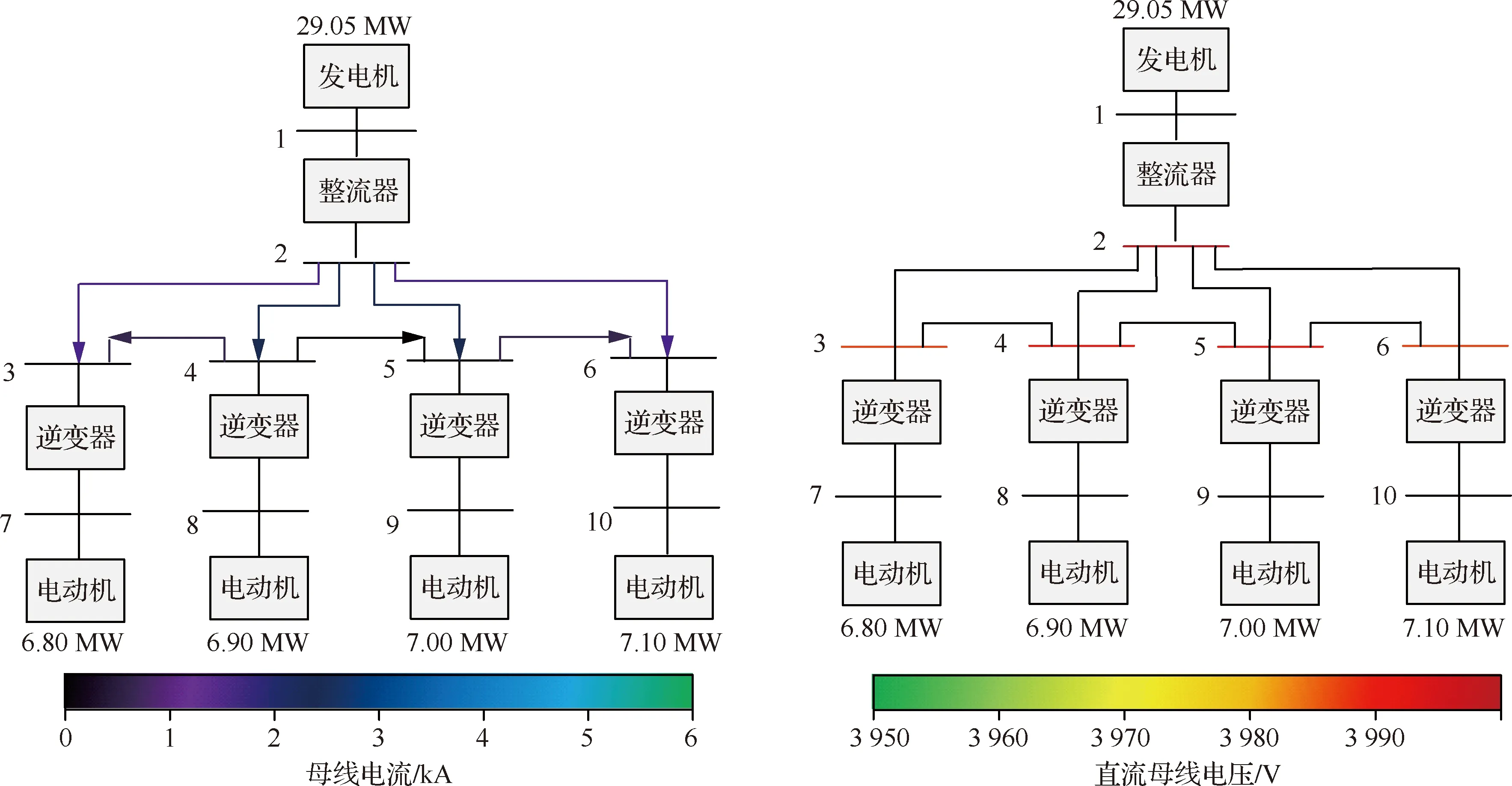
圖4 負載功率間距0.1 MW穩定運行狀態

將負載功率的間距值增大到0.4 MW，如圖5所示，從分析結果中可以看出，由于左側電動機負載的功率變得更小，左側直流輸電線上的電流密度也隨之進一步減小；同時冗余輸電線的電流密度也呈現成同樣的趨勢，負載功率較小的一側電流減小，較大的一側電流增大。

圖5 負載功率間距0.4 MW穩定運行狀態

在母線電壓方面，由于左側直流輸電線上的電流減小，母線3的電壓有所上升，母線4的電壓上升幅度很小，基本沒有變化。值得注意的是發電機提供的有功功率發生了大幅度的下降，下降了0.21 MW，反映出負載功率不平衡運行狀態有利于節約供電系統的能量損耗。

1.2.3 斷路故障運行狀態分析結果

在飛機運行過程中，除了分析穩定運行狀態外，更重要的是分析系統發生故障時輸電線的電流密度與直流母線電壓的變化情況。本文選擇了對直流輸電線故障這一運行狀態進行分析，考慮了單線斷路與雙線斷路2種故障狀態，并且保證電動機負載的總功率與負載對稱穩定狀態下相同。具體的分析結果如下所述。

1) 單線斷路

如圖6所示，斷路的直流輸電線被標為灰色。分析結果表明，由于存在輸電線斷路，沒有發生故障的直流輸電線上的電流都有不同程度的增大，并且與斷路的輸電線相鄰的輸電線電流增加幅度最大，這是因為原本應由斷路的輸電線提供的電流被分配到了該輸電線上，同時連接中間兩個逆變器的冗余輸電線上流過了較大的電流，這說明該冗余輸電線在故障情況下可以起到重新規劃系統能流路徑的作用。

圖6 單線斷路故障運行狀態

從母線電壓分析結果中可以看出，發生斷路故障的母線3的電壓有明顯的下降，而其他直流母線電壓的下降幅度沒有這么大。由于斷路故障使得整個配電系統的能流傳輸路徑變長，發電機需要提供的有功功率與正常運行狀態相比增大了0.025 MW。

可以看出，單線斷路會引起配電系統其余輸電線的電流密度增大，母線電壓下降，同時發電機需要提供的總功率變大。

2) 雙線故障

如圖7所示，在左側的兩根直流輸電線完全斷路的情況下，與之距離最近的輸電線上的電流大大增加，同時為了平衡系統的功率需求，最右側的輸電線電流也有所增加。

圖7 雙線斷路故障運行狀態

從母線電壓分析結果可以明顯看出，斷路故障側的直流母線電壓相較于單線故障時下降了許多，同時另一側的母線電壓也有一定程度的下降。為了彌補系統能流路徑加長帶來的損耗，相比于穩定運行狀態，發電機需要產生的有功功率增大到了29.22 MW，增加了約0.58%。

可以看出，雙線故障的潮流分析結果與單線故障時的趨勢相同，但變化的幅度更加明顯。

通過以上分析，得到了飛機在采用分布式布局、高壓直流供電體制時，配電系統在穩定運行狀態與故障運行狀態下的輸電線電流密度，母線電壓與發電機產生的功率大小，根據這些數據，可以為配電系統的輸電線電流等級與變換器的選型提供理論依據，同時為不同工作狀態下發動機軸功率需求變化提供理論數據。各種運行狀態下各母線電壓與輸電線電流密度的具體值分別如表2與表3中所示。

表2 直流母線電壓具體數據

1.2.4 直流母線電壓等級對電網的影響

從表3的分析結果可以看出，負載平衡狀態下電網中輸電線的最大電流密度為2 432.15 A，在雙線斷路情況下最大電流密度值上升到了5 211.97 A， 電流密度越大，對輸電線的載流量要求就越高，在同等長度下，輸電線的質量也就越大。通常情況下，希望飛機電網中的最大電流不超過1 000 A，顯然上述的分析結果已經遠遠超出了這一要求，這說明選取的母線電壓等級不夠合理，應當進一步提高直流母線的電壓值。因此，對提高母線電壓等級所帶來的電網最大傳輸電流與發電機輸出功率的變化進行了研究與分析。

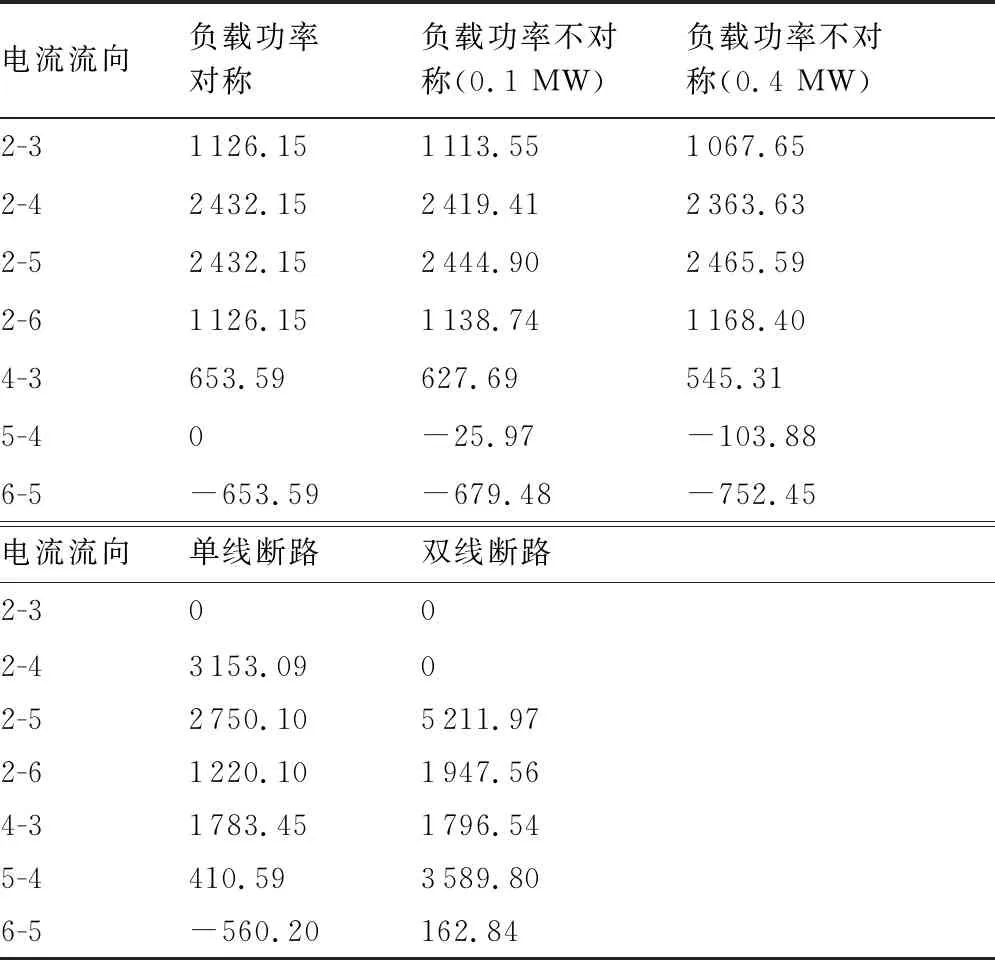
表3 直流輸電線電流密度具體數據

由于負載功率平衡情況與雙線斷路情況下輸電線的電流密度與發電機的輸出功率在所有情景下處于最大值，因此選擇了這兩種情況進行分析，分析結果如圖8與圖9所示。

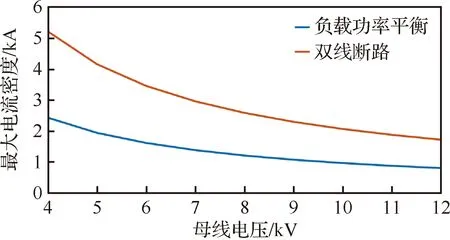
圖8 輸電線最大電流密度隨母線電壓變化關系

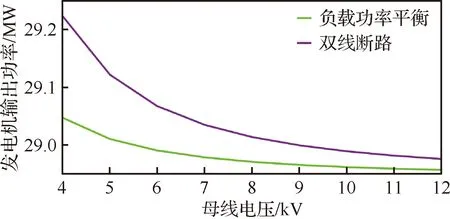
圖9 發電機輸出功率隨母線電壓變化關系

可以看出，隨著母線電壓等級的升高，輸電線的最大電流密度以及發電機輸出功率都在下降，并且曲線逐漸變得平滑，說明在母線電壓等級到達一定數值后，繼續增大對電網的影響將變小。在母線電壓升高到10 000 V時，輸電線電流密度下降到了1 000 A以下，此時雙線斷路故障情況下的最大電流也僅有2 067 A，繼續增大母線電壓，雖然電流密度與發電機功率可以進一步減小，但過高的電壓會降低飛機電氣系統的安全性，綜合各種因素考慮，對于該電氣系統，直流母線電壓選擇在9 000～10 000 V之間最為合適。

2 動力系統仿真模型

在第一部分中，對分布式電推進飛機電氣系統的能量流動情況進行了研究，但是，完整的電推進飛機動力系統不僅包括電氣系統，還包括了推進系統，只有將推進系統產生的推進功率與電動機的電功率相耦合，得到的電氣系統的功率分布情況才是有意義的。由于第1章中研究的動力系統總的推進功率較大，給系統各部件具體參數的設置帶來了一些困難，因此本章在SIMULINK環境下，針對某小型電推進飛機混合動力系統，分別搭建了其純電推進架構和渦輪-電推進架構仿真模型，并對其電氣系統的性能進行了相應分析。

2.1 混合動力系統組成

本文分析了純電推進和混合動力推進2種架構，2種架構的主要區別在于純電推進架構僅由儲能裝置提供能量，而渦輪-電推進架構是由發電機與儲能系統共同提供能量。從圖10中可以看出，電推進飛機動力系統主要由供電系統、儲能系統與推進系統3部分組成。

圖10 混合動力系統架構

2.2 仿真模型搭建

模型被劃分為飛行控制信號模型、飛機的氣動模型、配電系統模型、儲能系統模型與渦輪發電系統模型，具體使用到的組件包括發動機、發電機、整流器、鋰電池組、DC-DC變換器與電動機，模型中共有4臺推進器，并認為飛機推力被平均分配到4臺推進器上，整體仿真模型如圖11所示。進行仿真的目的在于分析動力系統的能量流動與功率分配關系，因此所選用的模型都是系統級參數化模型。

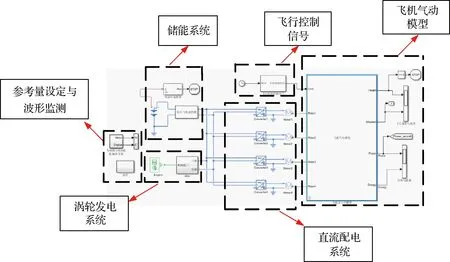
圖11 渦輪-電架構仿真模型

由于純電推進系統架構與渦輪-電推進系統架構相比，僅僅不包含渦輪發電系統，因此純電推進系統的仿真模型圖在此處不再給出。

在電推進動力系統的設計階段進行仿真實驗時，通常會采用后向仿真計算方法來實施系統仿真。所謂后向計算方法是指在已知系統運行狀態的條件下，根據運行狀態從后向前計算出系統處于穩定運行狀態時能流路徑上每一個部件的功率需求，采用這種仿真方法的優勢在于能夠計算出系統在給定工況下全部部件的運行狀態，為系統的方案設計與部件選取提供重要的參考信息。

在這種仿真方法中，需要已知飛機的飛行剖面。在本文中分別設計了基于時間與基于高度的兩種飛行剖面。

2.2.1 基于時間的飛行剖面

如圖12所示，基于時間的飛行剖面共包括5個階段，依次為滑跑—起飛—爬升—巡航—下降，通過定義飛機在每個飛行階段的航跡角與迎角，可以計算得到具體的推力需求，以及飛機的需求推進功率，將需求功率作為配電模型的輸入量，就可以實現推進系統與電氣系統的耦合。

圖12 基于時間的飛行剖面

2.2.2 基于高度的飛行剖面

采用基于時間的飛行剖面有利于分析飛機動力系統在每個飛行階段以及過渡階段的能量流動情況，但這種設計方式的缺點在于不能充分反映飛機實際的工作狀態。在實際情況中，飛機通常會在達到預定的高度后進入巡航狀態，在能量將要耗盡時返航。為了分析這種情況中渦輪-電推進與純電推進架構航程的差異，設計了基于高度的飛行剖面，如圖13所示。此時，飛機不再包括下降階段，在飛行高度達到300 m時進入巡航狀態，在電池的荷電狀態(SOC)下降到35%時，仿真停止。

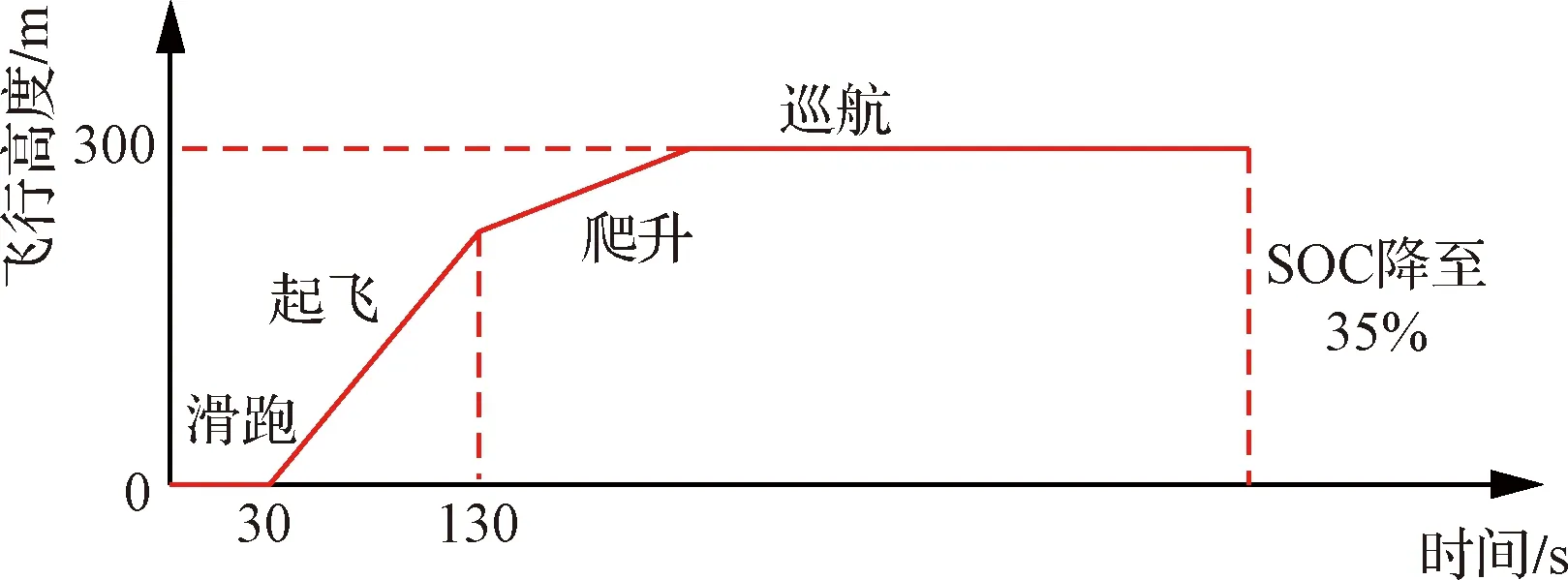
圖13 基于高度的飛行剖面

2.2.3 推進系統推力計算

為了實現電推進飛機動力系統的完整仿真，需要計算出推進系統的輸出機械功率，從而建立其與供電系統輸出電能的耦合關系。因此下面將具體分析飛機的氣動模型，推導飛機的空氣動力計算數學公式。

圖14為飛機受力分析示意圖，其中L表示飛機機翼產生的升力，D表示機體受到的阻力，T表示推進器提供給飛機的推力，方向與機翼弦線方向一致；α為飛機的迎角，指速度方向與機翼弦線之間的夾角，飛機飛行時機翼上的空氣動力與迎角有關；γ為航跡角，是飛機相對地面的運動方向夾角。

圖14 飛機受力分析示意圖

機翼產生升力的大小可以用如下式(7)表示，計算物體的阻力大小所采用的公式與計算升力的方法相似[21]。

(7)

(8)

式中:ρ為當前飛行高度下的空氣密度；V為飛機與氣流的相對速度(飛行速度)；Sw為翼展面積；CL與CD分別為升力系數與阻力系數。

將飛機的受力情況按照飛行速度方向進行分解，分別在速度方向及其垂直方向上可以得到如下受力平衡公式：

Tsinα+L=mgcosγ

(9)

Tcosα-D-mgsinγ=ma

(10)

只要得到了飛機的航跡角γ與迎角α，就可以根據式(9)計算出推力器提供的推力大小，在得到推力的值后，代入式(10)中，可以計算出飛機的加速度，再經過積分后，就可以算出飛機的飛行速度。有了這兩個物理量，推進器的機械功率便順勢得出，再根據推進器的效率曲線就能夠計算出供電系統所需提供的電功率。這樣，就實現了飛機推進系統與電氣系統的能量耦合。

2.3 仿真分析結果

采用基于時間的飛行剖面時仿真模型中各部件的主要參數設置的具體值如表4所示。

表4 仿真模型參數設置

2.3.1 推進功率與效率仿真結果

首先根據基于時間的飛行剖面對系統進行仿真，對比2種架構在不同飛行階段推進功率與效率的變化情況。

從圖15和圖16可以看出，渦輪-電推進架構下飛機的推進功率在全過程中都是大于純電推進架構的，并且呈現出相同的變化趨勢。在地面滑跑階段，推進功率線性增大，進入起飛與爬升階段后，由于迎角增大，飛機產生的推力大幅度減小，推進功率也隨之下降；在巡航階段，推進功率略有減小，與爬升階段基本相同；在最后的下降階段，由于飛機的重力勢能轉化為動能，不再需要推進器提供大部分能量，因此推進功率大幅下降。

圖15 渦輪-電推進架構推力與推進功率曲線

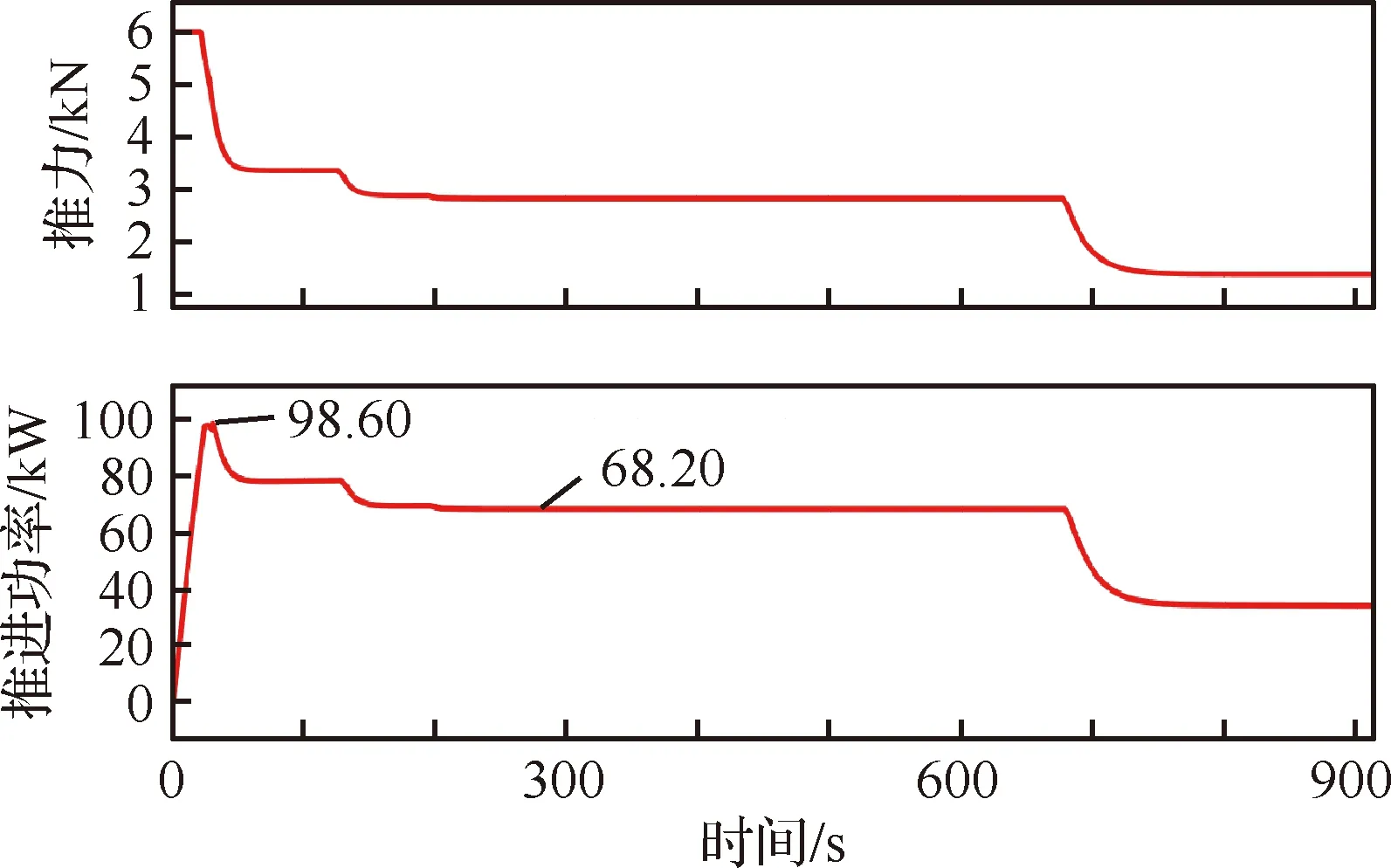
圖16 純電推進架構推力與推進功率曲線

飛機的推進效率曲線與推進功率的變化趨勢相同，隨著推進功率的下降而下降，同時純電推進架構的推進效率在全飛行過程中都是高于渦輪-電推進架構的，這是因為渦輪-電架構中含有效率較低的發動機部件。

2.3.2 供電系統功率分配仿真結果

從圖17可以看出，渦輪-電推進架構中，電動機的輸入電動率等于發電機與電池的輸出電功率之和。在地面滑跑階段，電動機的電功率需求從零開始不斷增大，在小于發電機的輸出電功率時，發電機為電池充電，在超過發電機電功率后，電池開始放電，在巡航階段，發電機的輸出功率與電動機輸入電功率基本持平，電池只需要提供4.92 kW的功率；在下降階段，電動機功率需求降低，電池再次進入充電狀態，充電功率為38.20 kW。由于純電推進架構中，電池提供了動力系統全部的能量，因此電池的功率變化趨勢與電動機的功率需求變化相同。

圖17 供電系統各部件功率曲線

由于兩種架構下電池的工作狀態完全不同，因此有必要在兩種架構下對電池的充放電曲線進行對比分析。

從圖18可以看出，在渦輪-電推進架構中，電池的SOC值最大下降到91.77%，在進入下降階段后，經過發電機充電，最終達到97.12%，而電池的SOC初始值為95%，全程消耗的燃油量為6.352 kg，經過整個飛行過程電池的電量是增加的，應當繼續優化系統的相關參數，使電池充放電平衡；在純電推進架構中，電池一直處于放電狀態，SOC最終下降到42.52%。同時，渦輪-電推進架構電池的最大充放電電流約為純電推進架構的58%，電池的過電流較小，系統更加安全。

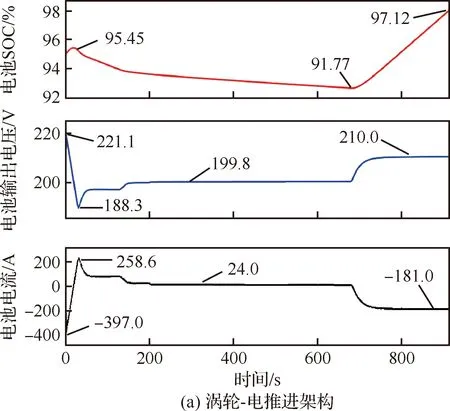
圖18 電池充放電曲線

2.3.3 供電系統功率分配仿真結果

在基于時間的飛行剖面下，飛機經歷了完整的飛行過程，比較2種架構下的航程沒有太大的意義。因此，采用基于高度的飛行剖面分析了航程與電池容量和任務載荷的關系。由于基于時間的飛行剖面中發動機的輸出功率較大，導致電池組的能量沒有得到充分的利用，因此將發動機的功率設置為70 kW，重新進行了仿真。

從圖19可以看出，航程隨電池容量的增大而增加，但由于飛機的總重也增加了，因此隨著電池容量的增大，航程的增加速率逐漸變慢。同時，對比2種架構可以發現，電池容量越大，兩者航程的差值越大，這說明在僅增大電池容量的情況下，渦輪-電推進架構有更好的效果。從圖20看出在電池容量恒定時，隨著任務載荷的增大，飛機的航程一直在減小，并且渦輪-電推進架構的下降速率明顯要高于純電推進架構，說明渦輪-電推進架構受飛機總重增加的影響更大。

圖19 航程隨電池容量的變化關系圖

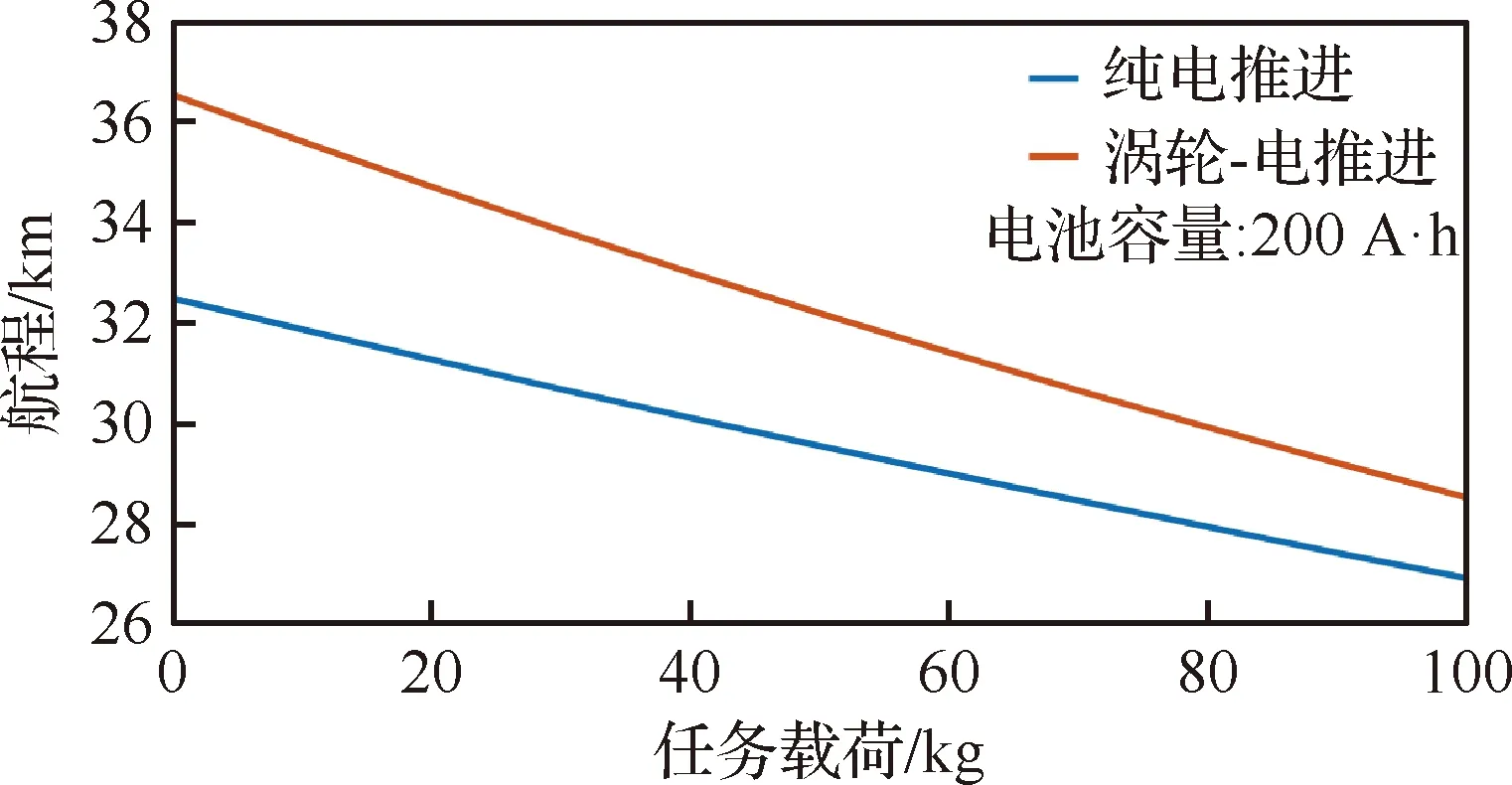
圖20 航程隨任務載荷的變化

由上面的分析可以發現，電池容量增大與任務載荷增大對兩種架構航程的影響是相反的，為綜合考慮兩種因素對飛機航程的影響，進一步繪制了電池容量、任務載荷與航程的三維關系圖。

從圖21中可以明顯看出，渦輪-電推進架構可以在更小的電池容量等級下達到選擇的航程臨界值，并且能夠承載更多的任務載荷，在航程方面是完全優于純電推進架構的。

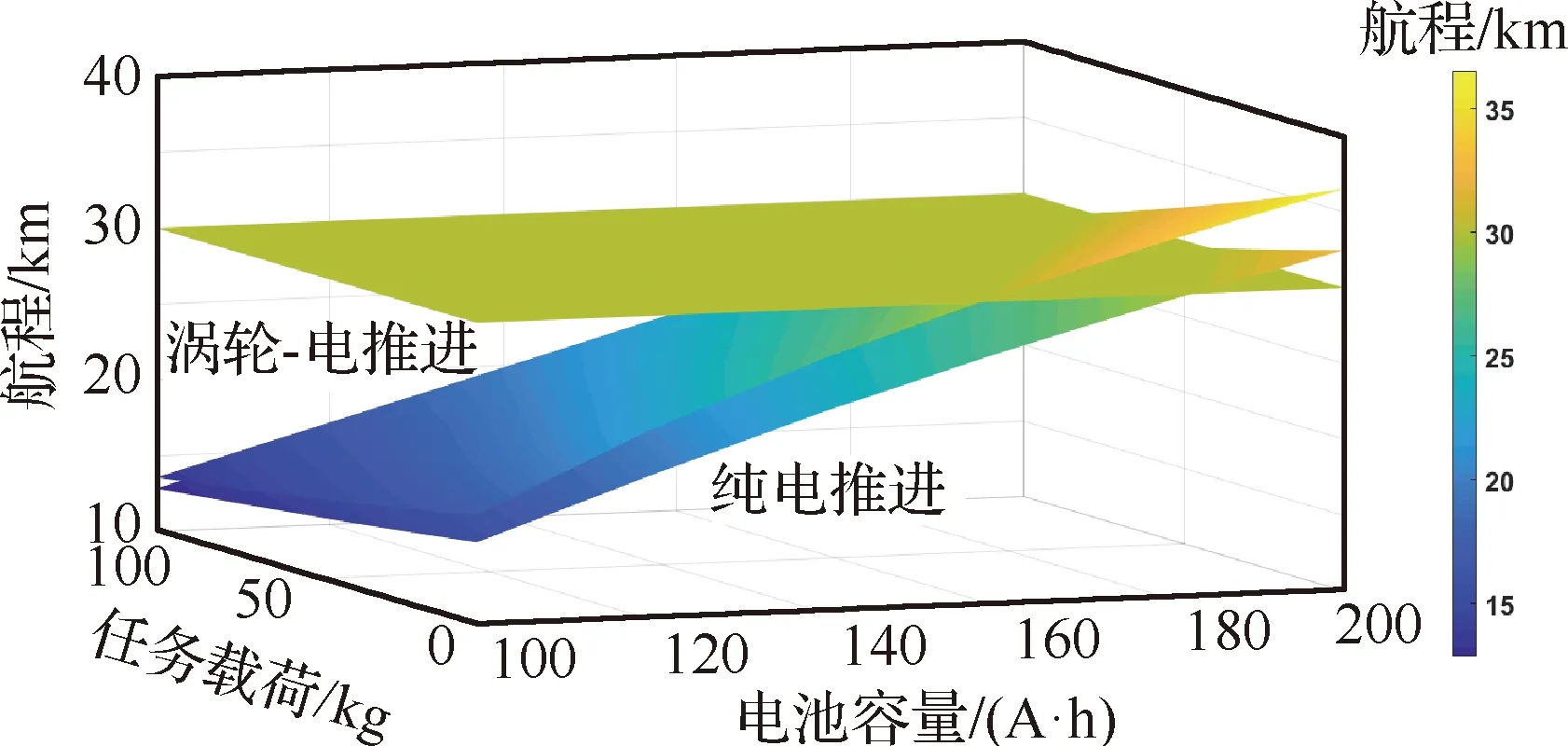
圖21 航程與任務載荷及電池容量的三維關系圖

3 動力系統參數化建模與優化

在第2部分中，搭建了動力系統完整的仿真模型，并對比分析了純電推進與渦輪-電推進架構的優劣。模型相關參數的設置是根據假定的功率重量比通過估算得到的，所建立的仿真模型精細度不高，為了解決這一問題，本部分建立了輸電線與電機的參數化模型，并利用符號規劃算法分別對其進行了優化分析，同時分析了傳統渦輪推進和渦輪電推進架構的動力系統總重與燃料消耗率之間的權衡關系。

3.1 符號規劃優化算法

符號規劃(SP)算法是幾何規劃(GP)優化算法的一種更通用的表示算法。幾何規劃算法主要用于解決具有非線性目標和約束條件的優化問題，由于其利用了拉格朗日對偶原理，因此可以把高度非線性方程轉化為具有線性約束的方程求解，同時可以確保全局最優解，為解決多學科飛機設計優化問題提供了獨特而強大的方法，因此目前已經被應用于飛機氣動模型的設計優化[22-23]。但是，并非所有飛機的設計約束都能夠滿足GP算法的約束條件，因此考慮通過減小設計約束來解決這一問題，即采用更一般化的SP算法。

在介紹符號規劃算法之前，首先對幾何規劃算法作簡單介紹，并簡要說明其優勢和局限性。

對于GP算法，只要存在可行的解決方案，求解器無需要求初始猜測值與實際的準確值接近就可以保證收斂到全局最優。

在GP算法中，目標函數和約束條件只能由單項式和多項式函數組成，其形式分別為

(11)

(12)

式中：aj為任意實數；ak、c、ck、uj為正實數。

簡單來說，GP算法受單項式等式約束和多項式不等式約束的約束，最小化了多項式目標函數，用數學語言描述GP算法如下：

minimizep0(u)

subject topi(u)≤1,i=1,2,…,np

mi(u)=1,i=1,2,…,nm

(13)

相比于GP算法，SP算法的最大優勢在于可以將ck的取值范圍擴展到全體實數，從而解決GP算法設計約束中常量系數不能取負的問題。但是SP算法中的目標函數不是凸函數，不能保證全局最優解，因此需要通過將GP算法中的函數形式轉換到對數空間中以將其轉化為凸優化問題。

經過代換，得到幾何規劃算法的數學描述為

(14)

式中：T表示連乘符號。

對式(14)取對數，目標函數與不等式約束函數將轉化為凸函數，等式約束函數是仿射函數，SP算法被轉化為凸優化問題。

本文利用了基于Python的GPkit[24]軟件包提供的SP算法，對建立的參數化模型進行優化分析,該軟件專門用于處理多學科領域的復雜優化問題。

3.2 關鍵部件參數化模型

3.2.1 輸電線參數化模型

假設輸電線由內導體層與外絕緣層組成，絕緣層的厚度要求能夠防止電介質擊穿，導體層的尺寸根據輸電線的最大傳輸電流決定。如圖22所示，輸電線截面中導體層半徑為a，外絕緣層的半徑為b。導體層采用絞合線以減輕由交流信號引起的趨膚效應與鄰近效應，可以看出，絞合線之間存在空隙，因此在導體層中有效導電面積并不能覆蓋整個導體層，設其占整個導體層的比例系數為kpf。

圖22 輸電線橫截面示意圖

根據橫截面，可以求出輸電線的有效導電面積Ac與外絕緣層橫截面積Adi分別為

Ac=πa2kpf

(15)

Adi=π(b2-a2)=π(b+a)tdi

(16)

式中：tdi=b-a表示絕緣層的厚度。

當輸電線絕緣層中的電場超過最大電場強度Emax時，絕緣層中的電介質會被擊穿，引起漏電。假設電介質的厚度非常小，電場強度的計算采用平行板近似，得到最大電場強度為

(17)

顯然，在輸電線的電壓一定時，對輸電線的厚度有最小值的限制要求。

假設輸電線的長度為lc，導體密度為dc，絕緣體密度為ddi，結合式(15)與式(16)，可以求出輸電線的質量為

mc=Aclcdc+Adilcddi

(18)

在計算輸電線傳輸效率時，將其當作電路中的恒定電阻處理，根據式(19)所示的輸電線電阻表達式與假定的輸出功率Pout，就能夠得到輸電線的效率表達式。

(19)

(20)

式中：ρc為導體材料電阻率。

選擇輸電線導體層半徑a與絕緣層厚度tdi作為設計變量，約束條件為式(17)，目標函數為式(18)，將其取最小值，使輸電線的總質量為最小。

3.2.2 電機參數化模型

電機的種類多種多樣，由于齒槽式永磁同步電機產生的轉矩大，效率高，在航空領域十分常見，因此在本文中選擇對該種電機進行建模。假設該電機為三相電機，并且每極中有3個齒槽。永磁同步電機通常由5部分組成，如圖23所示，分別為定子鐵芯、定子齒、繞組、永磁鐵和轉子鐵芯[25]。由于每一部分的幾何形狀不同，對其質量的計算方法也有所不同，下面將分別介紹各部件質量的建模方法[19]。

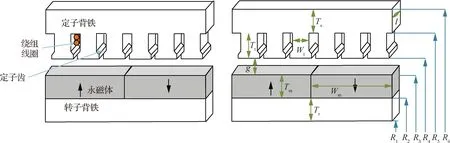
圖23 永磁同步電機結構示意圖

定子鐵芯與轉子鐵芯具有相同的圓柱形幾何形狀，因此兩者的質量計算公式類似。

轉子鐵芯的質量計算公式為

π(R2+R1)Trldrotor

(21)

式中：R1、R2為轉子鐵芯的內半徑與外半徑；Tr=R2-R1為轉子鐵芯的厚度；drotor為轉子材料的密度；Arbi為轉子鐵芯的面積。

定子鐵芯的質量計算公式為

π(R6+R5)Tsldstator

(22)

式中：R5、R6為定子鐵芯的內半徑與外半徑；Ts=R6-R5為定子鐵芯的厚度。

永磁體也可以看作圓柱體形狀，其質量計算公式與定子鐵芯相似，為

π(R3+R2)Tmldmag

(23)

式中：R3為永磁體的外半徑；Tm=R3-R2為永磁鐵的厚度。

假設單個定子齒的截面是厚度為Tt，寬度為Wt的矩形，電機中定子齒的總個數為6p，那么定子齒占據的總截面積Ateeth為

Ateeth=6pTtWt

(24)

假設定子材料的密度為dstator，可以得到定子齒的總質量為

mteeth=Ateethldstator

(25)

繞組線圈纏繞在定子齒上，定子齒與凹槽共同組合成的幾何體的內半徑為R4，外半徑為R5，且有定子齒厚度Tt=R5-R4，可以得到定子齒與凹槽的面積之和為

π(R5+R4)Tt

(26)

假設繞組線圈占定子凹槽的比例為kpf，線圈材料的密度為dcond，則凹槽中的繞組質量為

mwind,in=kpfAslotsldcond

(27)

除凹槽中的繞組外，還有一部分繞組纏繞在電機外部，將這部分繞組成為稱為端部繞組。假設端部繞組為三角形形狀，端部繞組末端的斜邊長度可以表示為[26]

(28)

式中:λ表示定子凹槽占定子總面積的比例。

綜合考慮兩部分繞組，可以得到繞組的總質量為

mwind=kpfAslots(l+2Let)dcond

(29)

電機的總質量為各部件的質量之和，如式(30)所示：

mmotor=msbi+mteeth+mwind+mmag+mrbi

(30)

電機的功率損耗主要包括歐姆熱損耗、渦流損耗與磁滯損耗，從輸入功率中減去以上損耗后，就可以得到電機的輸出功率，進而計算出電機的效率。

假設電機模型為交流三相電機，相電阻為總電阻的1/3，電流流過的截面積只考慮定子凹槽的部分，電機模型的電阻表示為

(31)

進而求出電機的歐姆熱損耗為

Pohmic=I2(2Rph)

(32)

渦流損耗Peddy與磁滯損耗Physt分別根據經驗公式計算得到[27]

(33)

(34)

式中:ke、kh分別表示渦流損耗系數與磁滯損耗系數;α1為指數擬合系數;f為主電源頻率;Bteeth為定子齒的磁通密度。

可以看出，這兩種損耗與定子齒和永磁鐵的質量，以及電機的旋轉角速度和極對數有關，并且隨著轉速的升高而增大。

電機的效率表示為

(35)

選擇轉子鐵芯的內半徑R1、厚度Tr，定子鐵芯的內半徑R5、厚度Ts，永磁體的厚度Tm，定子齒的厚度Tt，繞組線圈占定子凹槽的比例kpf，電機的軸長l等參數作為設計變量，約束條件為電機各部分的磁通密度小于其對應材料的飽和磁通密度，如式(36)～式(39)所示，最終目標函數為式(30)，將其取最小值，使電機模型總重最小。

(36)

(37)

(38)

(39)

式中:Brbi為轉子鐵芯的磁通密度;Bsbi為定子鐵芯的磁通密度;Bsat為定轉子材料的飽和磁通密度;Bgap為氣隙平均磁通密度;μ0為真空磁導率;M為磁化常數;g為氣隙厚度;Jm為電機的最大電流密度。

3.3 參數化模型優化結果

3.3.1 輸電線模型優化結果

從輸電線的效率表達式可以看出，在輸電線的輸出功率一定時，通過減小輸電線的電阻值或輸電線流過的電流值來提高效率，同時輸電線的電阻與導體材料的電阻率ρc和輸電線的長度lc成正比，與有效導電面積Ac成反比，在飛機的結構確定后，一般導體材料與輸電線長度不會再有變化，因此輸電線的電阻僅和有效導電面積Ac有關，增大有效導電面積可以減小輸電線的電阻值，提高輸電線效率，但同時會增加輸電線的重量。另一方面，通過提高輸電線的電壓等級可以減小輸電線電流，但同時會增大輸電線的絕緣層厚度，導致輸電線重量的增加。

綜上所述，輸電線效率的提高是以重量增加為代價的，同時與輸電線的電壓等級有很大關系。因此，利用優化算法得到了在不同電壓等級下，輸電線達到給定效率值的最小質量。

從圖24可以看出，隨著電壓等級的升高，在效率不變的情況下輸電線的質量逐漸減小，當電壓升高至300 V時，輸電線的質量基本不再發生較大的變化。同時，在同一電壓等級下，輸電線的質量隨著效率的增大而增加，在效率較小時，質量的增加速度并不是很大，但是在效率值達到99.5%之后，每提升0.1%輸電線的質量就會急劇增加，顯然，過分追求輸電線的高效率對于整個動力系統來說是得不償失的。

圖24 不同電壓等級下輸電線效率與質量的關系

3.3.2 電機模型優化結果

電機模型的優化分析結果會受到多種參數的影響[28]，在本文中選擇電機的轉速作為變量，以電機總質量最小為優化目標，利用優化算法，得到了電機質量與效率隨角速度的變化關系。

如圖25可以看出，隨著轉速的不斷上升，電機模型的總質量一直減小，而效率在短暫增大之后也一直減小。這是因為在輸入機械功率不變的情況下，角速度增大會導致發電機軸長、永磁鐵外徑、氣隙磁通密度、繞組線圈面積4種變量的同時或單個數值減小，繼而導致發電機總質量的減小。另一方面，最開始階段效率的增加是因為繞組線圈面積有所減小，導致線圈中流過的電流減小，歐姆熱損耗減小，此時由于角速度不大，渦流損耗與磁滯損耗占總功率損耗的比例較小，隨著角速度的不斷增大，這2種損耗在總損耗中占據了主要部分，導致發電機的效率降低。

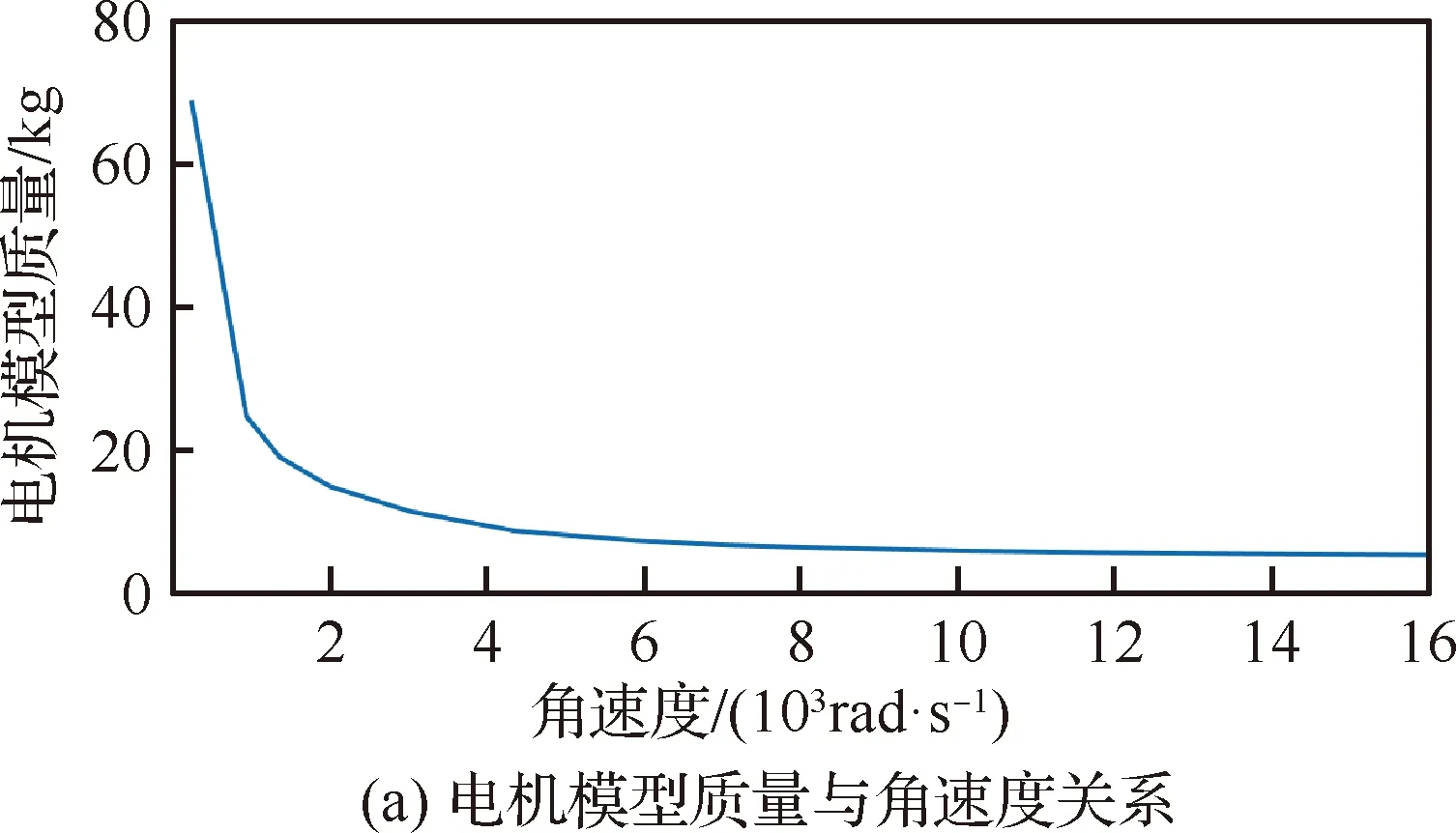
圖25 電機模型質量與效率隨角速度變化關系

3.4 動力系統整體模型優化結果

對輸電線與電機模型的優化分析可以看出，輸電線與電機的效率越高，其質量也會越高。為了獲得動力系統整體質量與效率之間的權衡關系，從燃料消耗率與動力系統總重兩個尺度對常規的渦輪推進架構與渦輪電推進架構進行了比較。

在渦輪推進架構中，渦輪風扇發動機直接與推進器涵道風扇連接；而渦輪電推進架構中，渦輪發動機驅動發電機轉動，產生的電能通過輸電線傳輸到電動機，再驅動涵道風扇產生推力。2種架構的具體配置方式如圖26所示。

圖26 推進系統架構示意圖

對兩種架構的系統總質量與油耗率之間關系的分析結果如圖27所示。

由圖27可以看出，在只有單臺涵道風扇的情況下，傳統的渦輪發動機推進架構相比于渦輪電推進架構更為輕便，推進效率也更高，并且動力系統總質量越小，渦輪發動機推進架構的效率優勢愈發明顯。這說明，如果不增加涵道風扇的數量，不考慮分布式布局下動力系統在氣體動力學上的效率提升，使用發電機和電動機將渦輪發動機和涵道風扇的機械功率進行解耦沒有系統級的收益。

圖27 兩種架構質量與燃油消耗率的關系

為了進一步得到動力系統主要部件的效率隨總質量的變化關系，針對渦輪電推進架構進行了分析，結果如圖28所示。

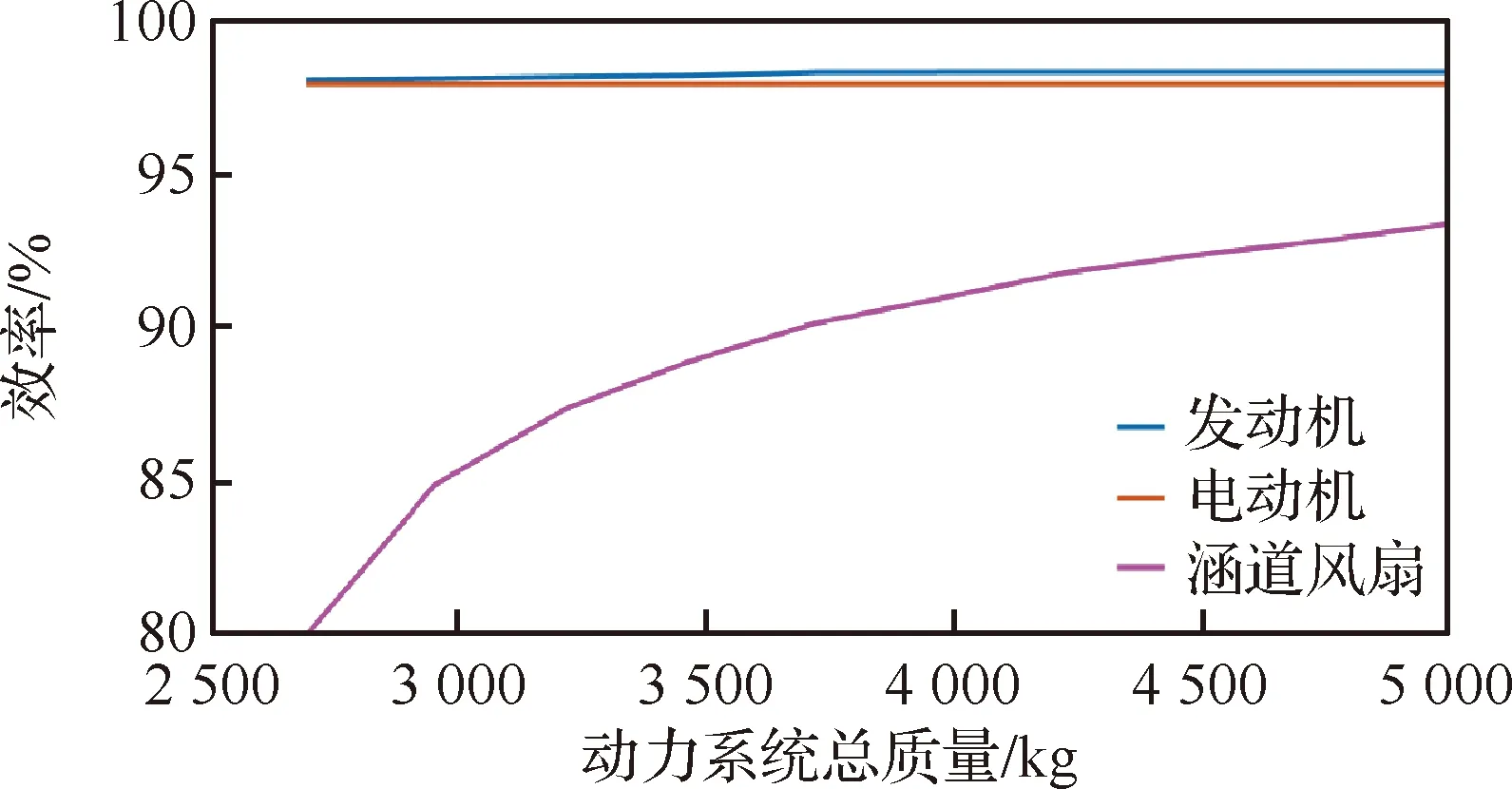
圖28 渦輪電推進架構主要部件效率與系統總質量關系

從圖28可以看出，如前文所述，電機與涵道風扇的效率隨系統總質量的增大而增加，發電機與電動機的效率的變化幅度很小，基本維持在98%左右；但是涵道風扇的效率變化很大，在質量最小點處，涵道風扇的推進效率僅有80%，在質量最大點處，效率增大到了92.8%。

4 結 論

電推進飛機作為當前研究的熱點，存在許多技術問題亟待解決，本文選擇電推進飛機混合動力系統作為研究對象，開展了分布式混合電推進飛機電力系統綜合優化和評估研究，所做的主要工作和主要結論總結如下：

1) 以未來的電推進大型客機高壓直流供電分布式布局電氣系統架構作為研究對象，參考地面交流電網的潮流分析方法，對飛機電網在負載功率平衡與不平衡狀態和斷路故障狀態下的變化情況進行了分析，同時研究了母線電壓等級對電網的影響。

2) 介紹了推進系統功率計算與電氣系統能量傳輸集成的耦合計算方法。在此基礎上，在SIMULINK環境下分別搭建了渦輪-電推進與純電推進動力系統架構的仿真模型，分析了兩種架構中各動力源部件的功率分配情況，比較了兩種架構的推進功率與效率，分析了航程隨電池容量與載荷質量的變化關系。

3) 建立了輸電線與電機的參數化模型，利用符號規劃算法對兩種模型分別進行了優化分析。對集成的渦輪直接推進與渦輪電推進架構進行分析，得到了其質量與效率的權衡優化結果。

未來的研究方向考慮在分布式多涵道風扇電推進飛機動力系統配置下，采用不同氣動外形和動力配置的飛機構型進行動力系統綜合分析，耦合如邊界層吸入(BLI)等因素的影響來研究其與動力系統的相互作用，同時建立其能量優化耦合模型進行分析求解，在以上基礎上考慮系統可靠性指標的綜合多目標優化。