航空機(jī)電作動器神經(jīng)網(wǎng)絡(luò)快速終端滑模控制
魏科鵬,胡健,姚建勇,邢浩晨,樂貴高
南京理工大學(xué) 機(jī)械工程學(xué)院,南京 210094
目前,航空作動器主要使用的是電液伺服作動系統(tǒng),但是隨著飛行器在農(nóng)業(yè)和安防等領(lǐng)域的應(yīng)用,對飛行器的靈活性、可靠性和日常維護(hù)提出了更高的要求。考慮到電液伺服系統(tǒng)存在噪聲大、油液污染及維護(hù)不方便等問題,而機(jī)電作動器相對干凈、無噪聲、靈活性高、維護(hù)方便,因此機(jī)電作動器受到越來越多的青睞。同時,以往航空作動器的控制大多集成在飛控計算機(jī)中,作動器與飛控計算機(jī)之間的電纜、接插件等附加設(shè)備的增加,大大降低了作動器的可靠性和安全性。因此目前針對作動器與控制器的一體化設(shè)計成為了研究熱點。但與此同時,控制器就要從原來的駕駛艙中移到作動器附近,其工況會變得異常惡劣,這就對機(jī)電作動器控制器的設(shè)計帶來很大的挑戰(zhàn)[1-2]。
為了提高機(jī)電作動器的控制性能,許多學(xué)者針對各種控制策略展開了大量的研究,目前比較常用的方法有:定量反饋理論、自校PID控制、前饋-反饋控制等[3]。上述控制方法均屬于線性理論下的線性控制策略,而航空機(jī)電作動器是一個具有多變量、非線性、強耦合的伺服系統(tǒng),因此傳統(tǒng)的基于經(jīng)典三環(huán)的控制方法越來越難以滿足實際的工況需要。近來,基于模型的先進(jìn)非線性控制方法得到了迅速的發(fā)展。針對控制系統(tǒng)的非線性問題,在文獻(xiàn)[4]中提出了反饋線性化控制方法,反饋線性化方法是將非線性數(shù)學(xué)模型轉(zhuǎn)化成線性數(shù)學(xué)模型,從而用線性理論解決系統(tǒng)的控制問題,其前提是需要知道精確的系統(tǒng)動力學(xué)特性及參數(shù),但是機(jī)電作動器本身存在負(fù)載變化、溫度變化而導(dǎo)致的電氣增益變化、磨損導(dǎo)致的摩擦系數(shù)變化以及未建模擾動,上述因素都導(dǎo)致難以獲得系統(tǒng)的精確模型,從而降低了反饋線性化控制器的性能;針對控制系統(tǒng)參數(shù)不確定的問題,文獻(xiàn)[5] 中提出了自適應(yīng)控制方法,自適應(yīng)控制方法能夠在模型參數(shù)不確定的情況下很好地對系統(tǒng)參數(shù)進(jìn)行估計并補償,但是當(dāng)系統(tǒng)中存在擾動時,其控制性能會大大下降;針對這一問題,文獻(xiàn)[6]中提出了自適應(yīng)魯棒控制策略,通過設(shè)計控制系統(tǒng)的非線性魯棒項,達(dá)到克服系統(tǒng)受到的外部干擾的目的。
自適應(yīng)魯棒控制(Adaptive Robust Control,ARC)具有較強的魯棒性,可以使系統(tǒng)在有擾動的情況下實現(xiàn)有界穩(wěn)定,為了加快控制系統(tǒng)的收斂時間,在文獻(xiàn)[7]中提出了終端滑模控制,終端滑模控制可以在有限時間內(nèi)將誤差收斂到零,同時也具備一定的魯棒性,為了進(jìn)一步提高系統(tǒng)的收斂速度,在終端滑模控制的基礎(chǔ)上,在文獻(xiàn)[8]中提出了快速終端滑模(Fast Terminal Sliding Mode, FTSM),該方法通過對滑模面的改進(jìn),進(jìn)一步提高了控制器的收斂速度[9],但是無論是終端滑模還是快速終端滑模,都有一個共同的缺點:滑模控制器會使控制量產(chǎn)生抖振,從而對控制系統(tǒng)產(chǎn)生損害[10-11]。
為了解決滑模的抖振問題,許多科研工作者設(shè)計了將其他控制策略與滑模相結(jié)合的控制方法,其中,神經(jīng)網(wǎng)絡(luò)控制(Neural Network Control, NNC)因其萬能逼近特性,能夠更好地解決滑模的抖振問題,神經(jīng)網(wǎng)絡(luò)控制在非線性控制領(lǐng)域已經(jīng)成為研究的熱門方向[12],Hornik等[13]發(fā)表了神經(jīng)網(wǎng)絡(luò)結(jié)構(gòu)方面的重要論文,在文中給出了多層神經(jīng)網(wǎng)絡(luò)擬合任何非線性函數(shù)的穩(wěn)定性證明,Thomas等[14]發(fā)表了多層神經(jīng)網(wǎng)絡(luò)在飛行器控制方面的應(yīng)用,并在形式上比較了神經(jīng)網(wǎng)絡(luò)控制與其他控制器在非線性控制中的區(qū)別。它是一個由多個簡單的結(jié)點(神經(jīng)元)相互連接起來的并行處理器,其優(yōu)點為在合適的結(jié)點權(quán)值下理論上可以擬合所有曲線,可以有效解決未知非線性系統(tǒng)難以處理的控制問題,近年來,許多學(xué)者使用神經(jīng)網(wǎng)絡(luò)和李亞普洛夫理論來證明控制系統(tǒng)的穩(wěn)定性和抗干擾能力,但是神經(jīng)網(wǎng)絡(luò)在學(xué)習(xí)過程中的參數(shù)重構(gòu)誤差是不可避免的,在文獻(xiàn)[15]中,設(shè)計了一種重構(gòu)誤差在線估計,并使用了對神經(jīng)網(wǎng)絡(luò)各層參數(shù)進(jìn)行自適應(yīng)設(shè)計以減少重構(gòu)誤差對系統(tǒng)性能的影響[16]。
本文針對航空機(jī)電作動器的組成和工作原理,建立了系統(tǒng)的數(shù)學(xué)模型,基于Lyapunov分析法設(shè)計了一種將多層神經(jīng)網(wǎng)絡(luò)與快速終端滑模結(jié)合的自適神經(jīng)網(wǎng)絡(luò)快速終端滑模(Adaptive Neural Network Fast Terminal Sliding Mode,ANNFTSM)的控制方法,該方法將系統(tǒng)參數(shù)不確定性和未建模動態(tài)統(tǒng)一歸入到系統(tǒng)的總不確定性中,然后用神經(jīng)網(wǎng)絡(luò)去觀測并加以補償,針對補償誤差設(shè)計非線性魯棒項加以克服,以減弱神經(jīng)網(wǎng)絡(luò)的重構(gòu)誤差對系統(tǒng)性能的影響,在實現(xiàn)了系統(tǒng)有界穩(wěn)定的同時使系統(tǒng)具有更快的收斂速度和更好的魯棒性能。
1 問題描述與數(shù)學(xué)模型
航空機(jī)電作動器是以機(jī)電系統(tǒng)作為動力輸出,配備位置傳感器、傳動裝置等,機(jī)電作動器有兩個驅(qū)動模式:直接驅(qū)動型和間接驅(qū)動型;本文研究的某型航空機(jī)電作動器采用的是間接驅(qū)動,電機(jī)輸出通過減速箱、滾珠絲杠帶動舵面進(jìn)行所期望的運動,結(jié)構(gòu)如圖1所示。
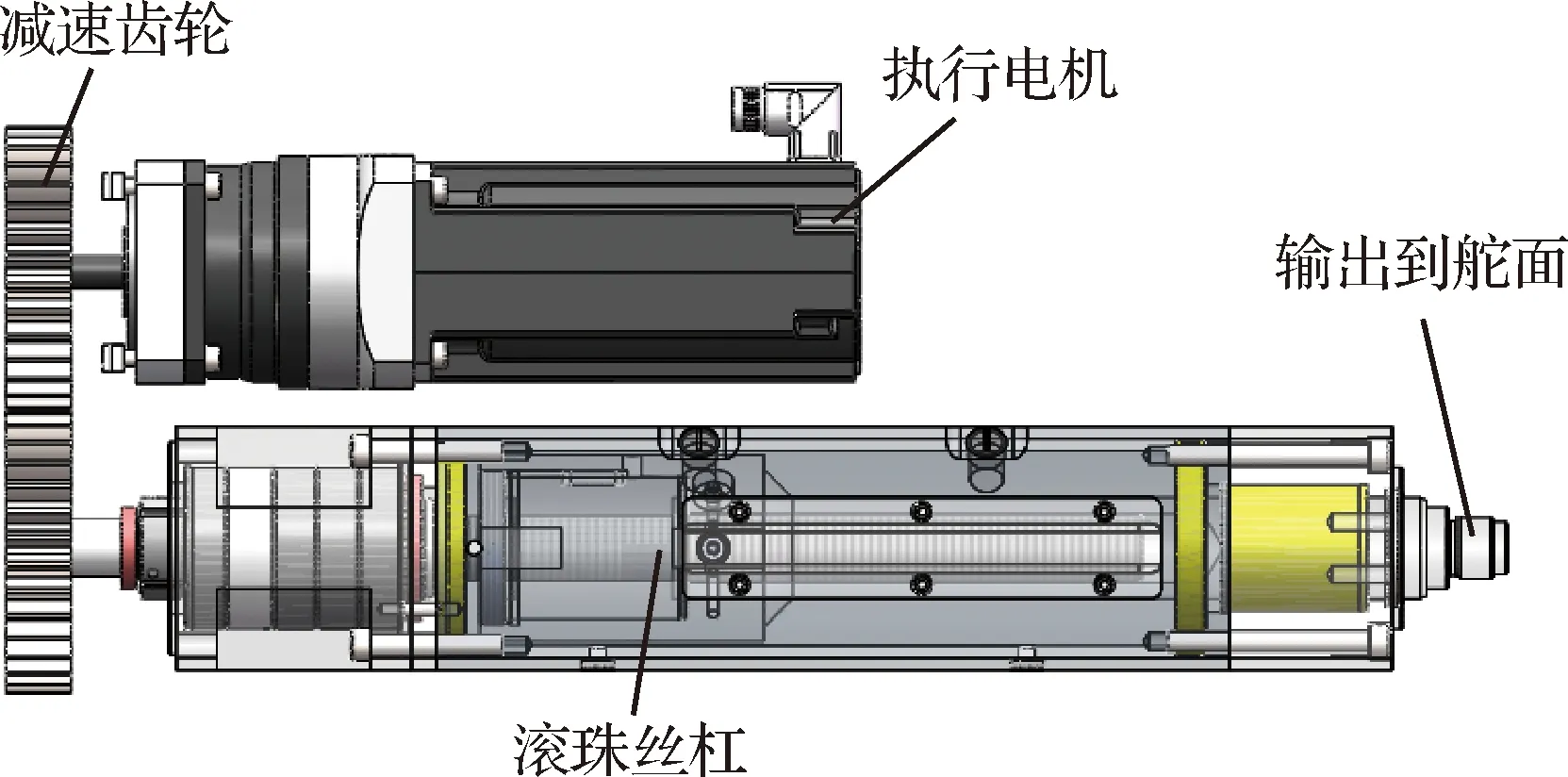
圖1 間接驅(qū)動型機(jī)電作動器原理圖
為了提高機(jī)電作動器系統(tǒng)的控制精度,在建立系統(tǒng)模型時需要考慮諸多非線性因素,如系統(tǒng)的粘滯、摩擦等。同時為了提高系統(tǒng)容錯能力,在建模的時候還應(yīng)考慮系統(tǒng)可能出現(xiàn)的故障。航空機(jī)電作動器較為常見的故障有:減速器斷齒、滾珠絲杠間隙過大等,其中減速器斷齒即減速器在運行過程中,齒面斷裂,產(chǎn)生齒輪質(zhì)心偏移,導(dǎo)致齒輪的輸出信號產(chǎn)生一個額外的正弦調(diào)制干擾;滾珠絲杠間隙過大可能由安裝不規(guī)范或磨損導(dǎo)致,該故障會導(dǎo)致螺母在運行過程中因為自身位移而產(chǎn)生轉(zhuǎn)動下滑,產(chǎn)生彈性位移,從而導(dǎo)致定位精度下降,超出系統(tǒng)能接受的范圍。這些故障都是比較典型的加性故障,即在原系統(tǒng)的基礎(chǔ)上出現(xiàn)故障干擾項[17]。因此,由牛頓第二定律,結(jié)合可能發(fā)生的加性故障,建立機(jī)電作動器系統(tǒng)的數(shù)學(xué)模型為
(1)
式中:J為負(fù)載折算到電機(jī)的轉(zhuǎn)動慣量;y為電機(jī)位置輸出量;ku為電機(jī)力矩系數(shù);B為作動器系統(tǒng)折算到電機(jī)的黏性阻尼系數(shù);dn為系統(tǒng)的不確定性和干擾;f(t)表示系統(tǒng)的加性故障;η(t)為加性故障發(fā)生的時間規(guī)律:
(2)
為方便設(shè)計控制器,機(jī)電作動器系統(tǒng)模型可表示為
(3)
式中:x為系統(tǒng)的狀態(tài)變量;x1為位置變量;x2為速度變量;u為控制系統(tǒng)的控制量;y為控制系統(tǒng)的輸出量;θ1=ku/J、θ2=B/J、d1=dn/J為系統(tǒng)受到的常值擾動;d2(t)=f(t)/J為外部干擾,為方便后序控制器設(shè)計,作出以下假設(shè):
假設(shè)1控制系統(tǒng)受到的擾動d1(t)是有界的,有|d|≤ξ,ξ∈C。
假設(shè)2控制系統(tǒng)的參數(shù)θ1、θ2在實際運行過程中是有界的。
2 控制器設(shè)計
相對于自適應(yīng)魯棒控制,快速終端滑模能夠在更快的時間內(nèi)使跟蹤誤差收斂到零,所以控制精度能夠提升一個數(shù)量級,快速終端滑模還具有一定的魯棒性,能夠補償一定范圍內(nèi)的干擾。
2.1 設(shè)計快速終端滑模控制器(FTSM)
在系統(tǒng)正常的工作環(huán)境下,當(dāng)給定一個指令信號yd的時候,系統(tǒng)會輸出信號y去跟蹤指令信號,其中y=x1、yd=xd,控制目標(biāo):t→∞時,(y-yd)→0。
當(dāng)航空機(jī)電作動器系統(tǒng)不存在加性故障時,η(t)=0,狀態(tài)方程可寫為
(4)
假設(shè)3系統(tǒng)的指令信號xd滿足xd(t)∈C2且是有界的。
令位置跟蹤誤差:
e0=xd-x1
(5)
設(shè)計滑模面s1:
(6)
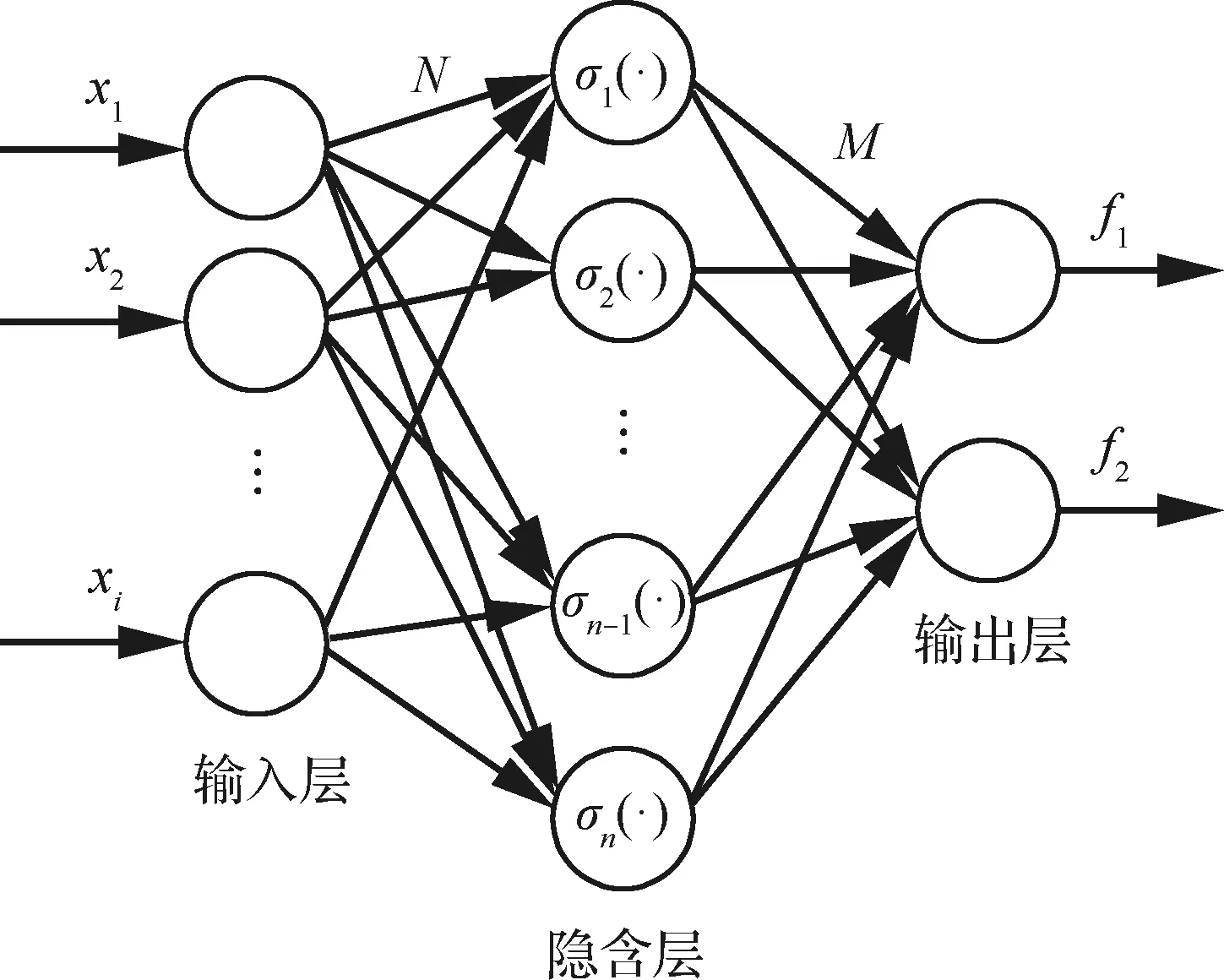
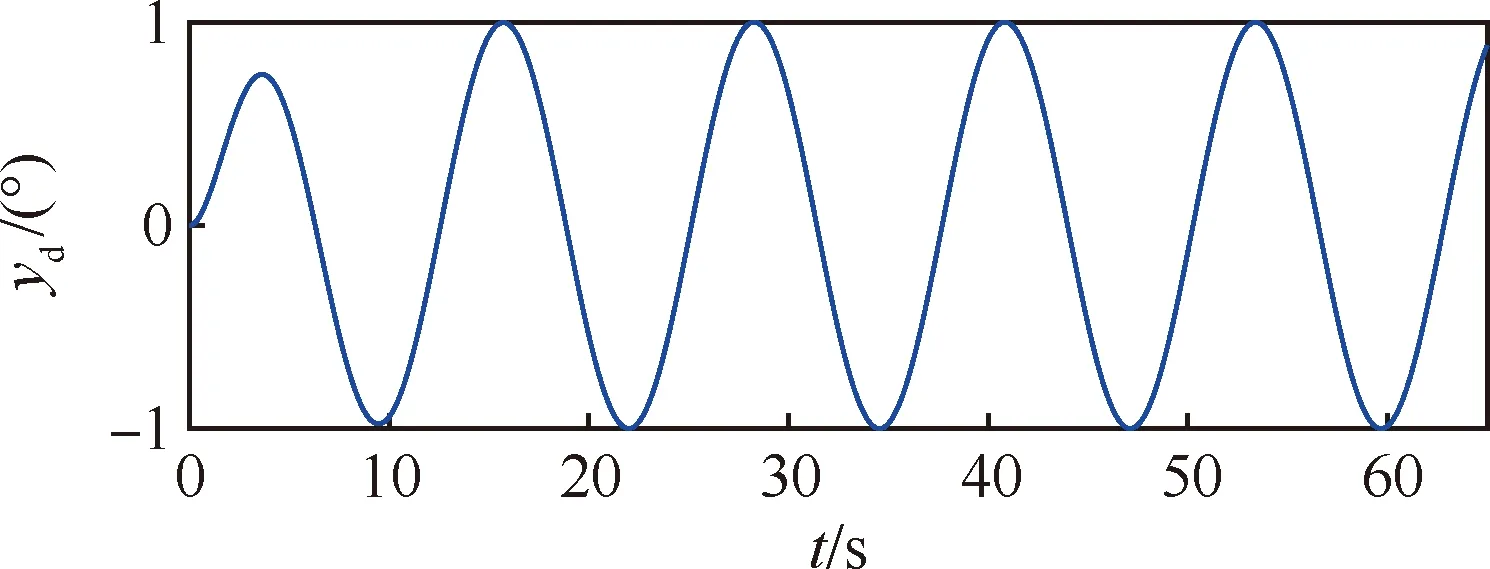
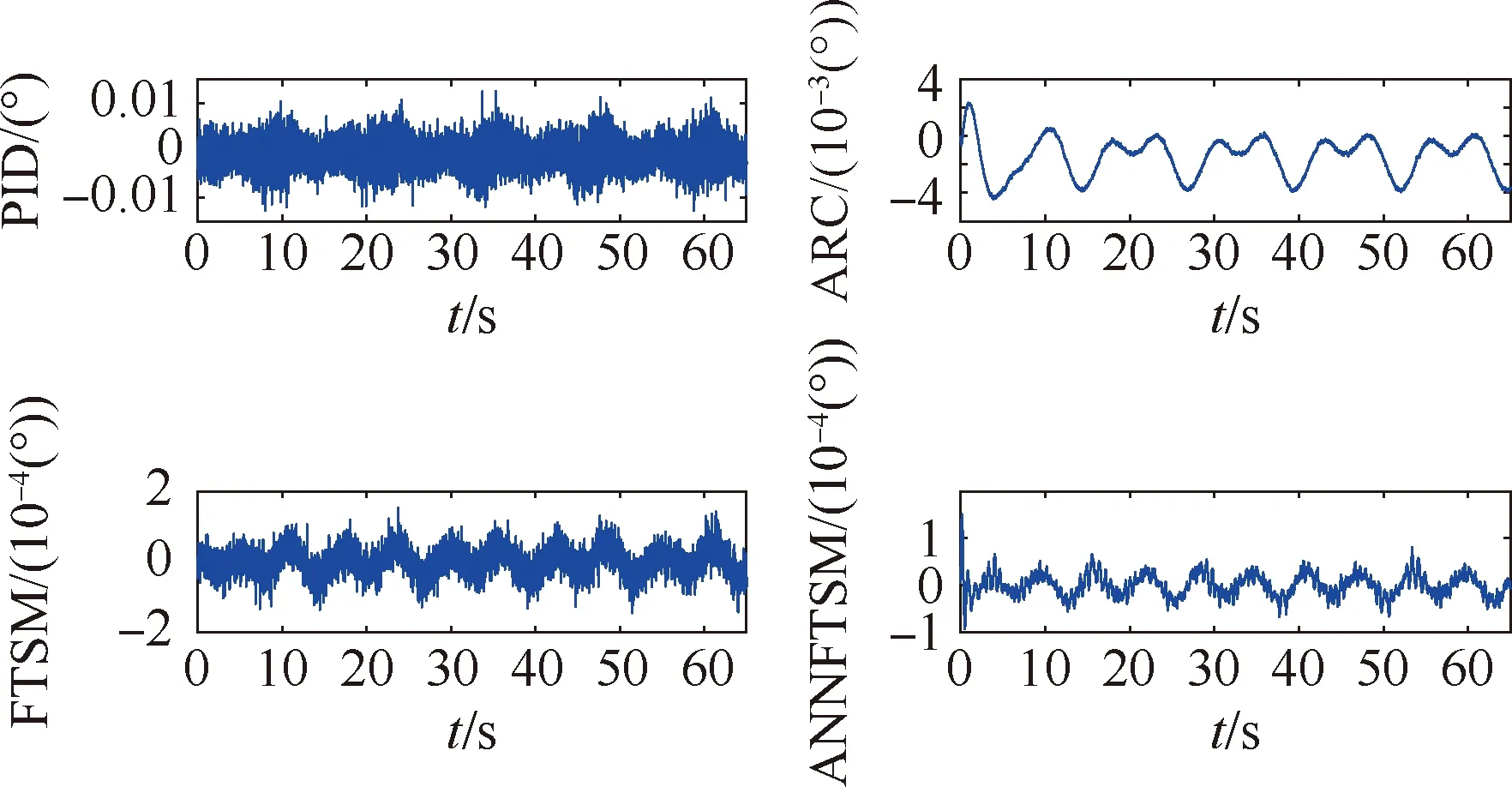
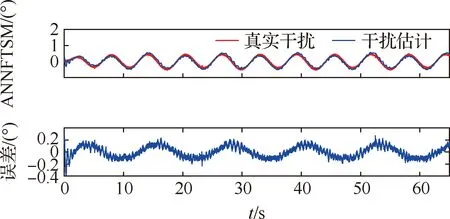
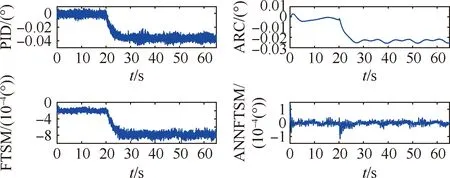
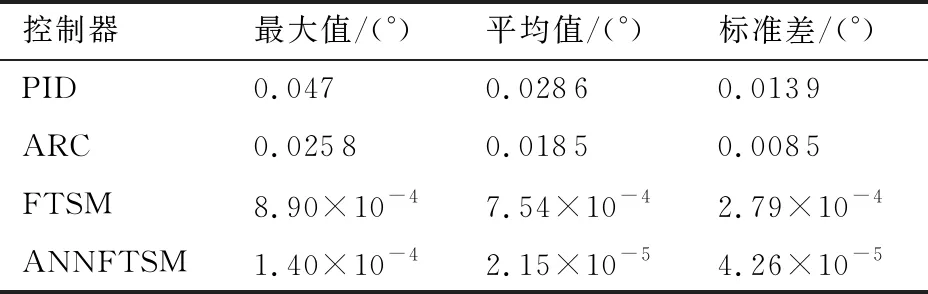
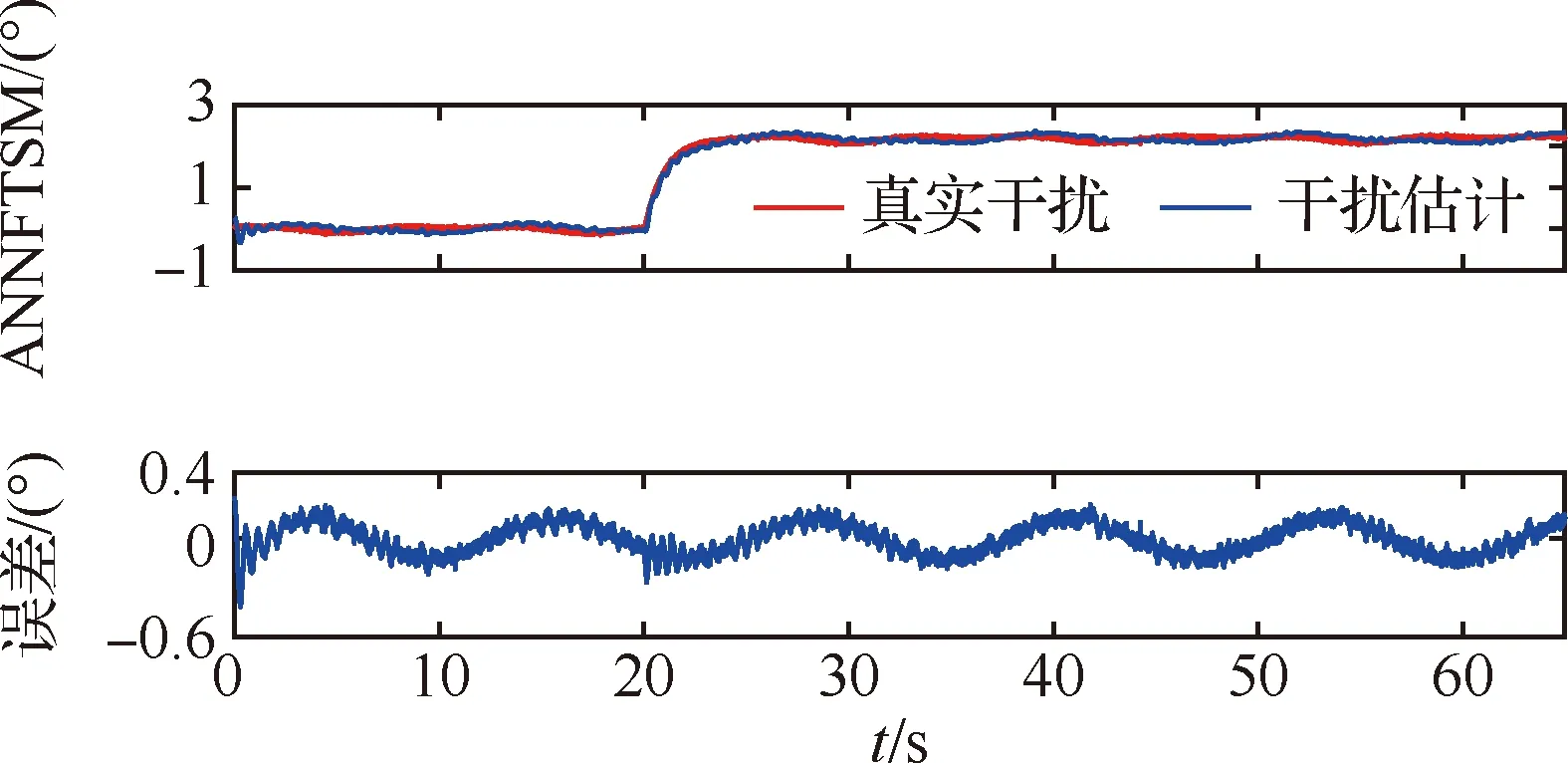
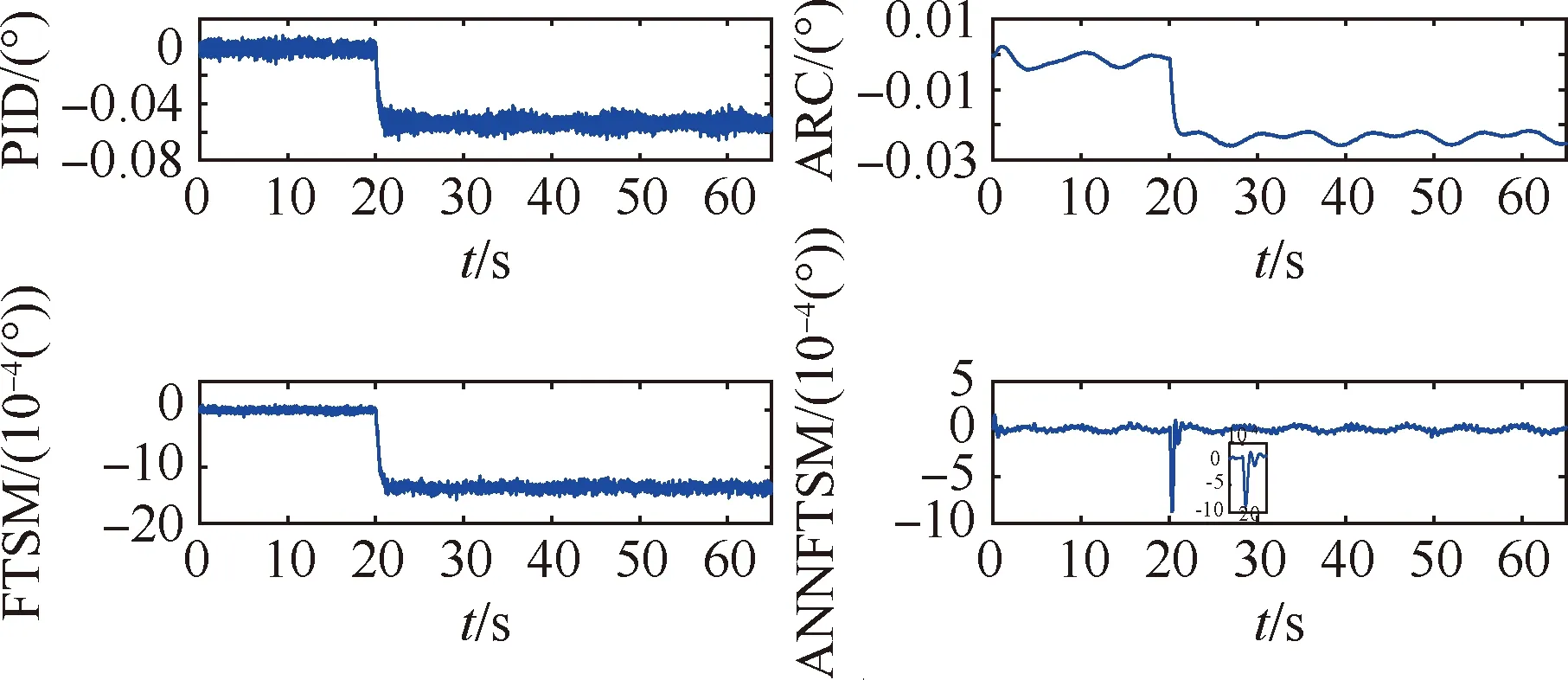
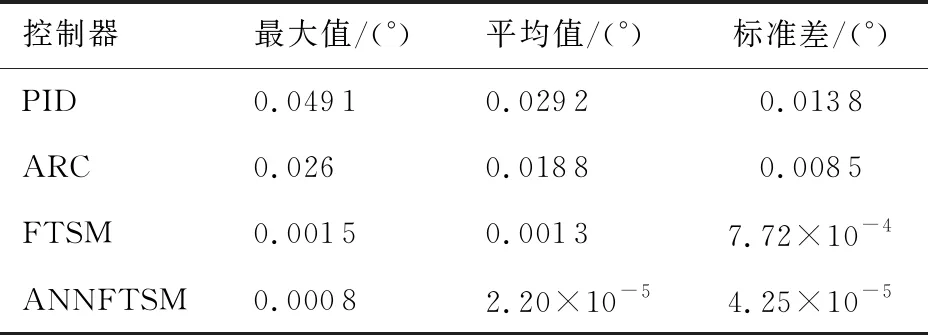
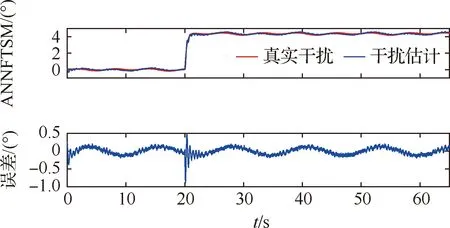
式中:α1<0,β1>0,p1和q1是大于零的數(shù),q1為奇數(shù),0 (7) (8) u=u1+u2 (9) (10) (11) 其中:φ>0,γ>0。將式(9)代入式(8),可得: -θ1u2-d1 (12) 引理1假設(shè)存在連續(xù)正定函數(shù)V(t)>0,如果要想在有限時間ts內(nèi)讓V(t)收斂到0,必須滿足下面的不等式[18]: (13) 式中:μ>0,λ>0,0<ζ<1,同時 (14) 定理1根據(jù)引理1,在式(9)~式(11)的作用下,航空機(jī)電作動器控制器可實現(xiàn)有限時間穩(wěn)定。 證明:設(shè)計李亞普洛夫函數(shù)如下: (15) 對式(15)求導(dǎo): (16) 簡化式(16)可得: (17) 根據(jù)引理1,可得設(shè)計的滑模面s1在有限時間ts內(nèi)收斂,控制系統(tǒng)可以達(dá)到有限時間穩(wěn)定。但是,上述系統(tǒng)的前饋項是建立在系統(tǒng)參數(shù)θ1、θ2準(zhǔn)確值已知的情況下,在實際的航空機(jī)電作動器系統(tǒng)中,系統(tǒng)精確參數(shù)的準(zhǔn)確值是很難得到的,這也會嚴(yán)重影響上述系統(tǒng)在實際運行中的精度,同時該控制器沒有考慮系統(tǒng)可能發(fā)生的故障,對故障的容錯能力有限,加上快速終端滑模自身抖振的原因,如果系統(tǒng)發(fā)生故障,可能會對故障起激勵作用。綜上所述,快速終端滑模在實際的運行中是很難實現(xiàn)的[19]。 為了克服上述快速終端滑模控制器在實際運行過程中的缺陷,本文結(jié)合快速終端滑模控制器的優(yōu)點,引入神經(jīng)網(wǎng)絡(luò),設(shè)計了自適應(yīng)神經(jīng)網(wǎng)絡(luò)快速終端滑模控制器,在改善控制性能、解決FTSM抖振的同時,提高系統(tǒng)容錯性能。 已知參數(shù)的真值θ1、θ2為未知項,令參數(shù)名義值為θ1n、θ2n,參數(shù)不確定項為Δθ1、Δθ2,可得θ1=θ1n+Δθ1、θ2=θ2n+Δθ2,同時假設(shè)控制系統(tǒng)存在加性故障,原控制系統(tǒng)可表示為 (18) 為了方便處理未知項,可令 D=Δθ1u-Δθ2x2+d1+η(t)d2(t) (19) 將式(19)代入式(18)可得: (20) 本文采用神經(jīng)網(wǎng)絡(luò)觀測器觀測總擾動D,神經(jīng)網(wǎng)絡(luò)在理論上可以擬合任何函數(shù),因為其逼近能力和強大的學(xué)習(xí)能力,使得神經(jīng)網(wǎng)絡(luò)在智能非線性控制領(lǐng)域非常受歡迎,結(jié)構(gòu)如圖2所示, 由文獻(xiàn)[20]可得,神經(jīng)網(wǎng)絡(luò)的擬合公式為 圖2 神經(jīng)網(wǎng)絡(luò)結(jié)構(gòu)示意圖 y=WTσ(VTX)+ε(x) (21) 在本文中,擬采用3層神經(jīng)網(wǎng)絡(luò),滑模面仍然采用快速終端滑模控制器中的設(shè)計,用神經(jīng)網(wǎng)絡(luò)的輸出去擬合系統(tǒng)的總擾動D,由神經(jīng)網(wǎng)絡(luò)的逼近特性可得,存在權(quán)值向量W、V,使得: D=WTσ(VTX)+ε (22) (23) (24) usw=φ1s1 (25) (26) 將式(23)~式(25)代入式(26),可得: (27) 引理2 (28) 式中: 由式(28)可得δ(t)有界,存在常數(shù)hs,使得|δ(t)|≤hs。 根據(jù)引理2,可得: (29) (30) 設(shè)計神經(jīng)網(wǎng)絡(luò)權(quán)值自適應(yīng)律: (31) (32) 式中:rw>0,rv>0。 定理2在式(23)、式(24)、式(30)~式(32)的作用下,航空機(jī)電作動器控制器可以實現(xiàn)有界穩(wěn)定。 證明:設(shè)計李亞普洛夫函數(shù): (33) 對L2求導(dǎo),根據(jù)引理2,可得: (34) 將式(31)和式(32)代入到式(34),可得: (35) 根據(jù)引理3,將式(30)代入式(35),可得: (36) 引理4 根據(jù)引理4,式(36)可轉(zhuǎn)化為 (37) (38) 由式(38)可得出: L2≤-2λ1L2+λ2 (39) 由式(39)可得,控制器可以實現(xiàn)有界穩(wěn)定。定理2得證,控制流程如圖3所示。 圖3 控制流程圖 為了驗證本文所提算法的有效性,本文對快速終端滑模和結(jié)合了神經(jīng)網(wǎng)絡(luò)的快速終端滑模進(jìn)行了實驗研究,并和PID、自適應(yīng)魯棒控制器在控制精度和響應(yīng)速度上進(jìn)行對比,實驗平臺如圖4所示。 圖4 實驗平臺示意圖 本實驗臺模擬航空作動器的組成與功能,采用kollmorgen伺服電機(jī)作為動力源輸出,旋轉(zhuǎn)編碼器使用海德漢高安全性位置測量系統(tǒng),扭矩傳感器使用CD1140系列扭矩傳感器,本實驗通過加擾動的方式模擬作動器系統(tǒng)中的傳動元件和外部干擾對系統(tǒng)的影響。 實驗分為3種工況: 工況1正常情況下;系統(tǒng)只受到正常的外界干擾和模型不確定的時候,即η(t)=0時,此時收到正常的外界干擾f0=2x1x2(N·m)。 工況2當(dāng)系統(tǒng)滾珠絲杠發(fā)生間隙過大的情況時,這類故障通常是由磨損造成的,故障的發(fā)生是慢慢積累的,通過在實驗平臺上加小幅值緩變型故障f1=(1-e-0.5(t-20))(2.5+2x1x2) (N·m)實現(xiàn),f1在t=20 s時發(fā)生小幅值緩變型故障。 工況3當(dāng)系統(tǒng)減速器發(fā)生齒輪斷裂時,系統(tǒng)會突然增加1項故障干擾項,通過給試驗臺系統(tǒng)加載突發(fā)性加性故障,f2=(1-e-3(t-20))(5+2x1x2) (N·m)實現(xiàn)的,f2在t=20 s時發(fā)生小幅值緩變型故障。 實驗系統(tǒng)系數(shù)θ1=7.834、θ2=0.853,假設(shè)系統(tǒng)參數(shù)θ1n=9、θ2n=0.9,可得實驗?zāi)P腿缦拢?/p> (40) 4種控制器參數(shù)設(shè)計原則及取值: 1) 基于PID的作動器系統(tǒng)參數(shù)設(shè)計原則:kp增大可以加快響應(yīng)速度、減小系統(tǒng)穩(wěn)態(tài)誤差和提高控制精度,但是kp過大會產(chǎn)生較大超調(diào),甚至導(dǎo)致不穩(wěn)定;加大ki有利于減小系統(tǒng)靜差,但過分的積分作用會使超調(diào)加劇,甚至引起振蕩;增大kd有利于加快系統(tǒng)響應(yīng),使超調(diào)量減小,增加穩(wěn)定性,但也會帶來擾動敏感,抑制外干擾能力減弱。若kd過大則會使響應(yīng)過程過分提前制動從而延長調(diào)節(jié)時間。根據(jù)實際調(diào)試,參數(shù)如下:kp=10、ki=0.1、kd=-0.06。 3) 基于FTSM的作動器系統(tǒng)參數(shù)設(shè)計原則如下:α增大可以使系統(tǒng)的跟蹤誤差減小,但是太大的α?xí)?dǎo)致局部抖振加劇,進(jìn)一步導(dǎo)致發(fā)散;較小的α?xí)?dǎo)致系統(tǒng)精度降低;β過大或者過小都會導(dǎo)致系統(tǒng)精度下降、加劇震蕩;因為在控制器迭代的過程中需要對負(fù)數(shù)開q次方根,所以q只能取正奇數(shù),q應(yīng)該取較小的值,q增大會導(dǎo)致局部不穩(wěn)定,從而導(dǎo)致失敗;p只能取(0~q)之間的整數(shù),p增大可以減小系統(tǒng)的誤差;φ增大會使系統(tǒng)誤差減小,精度提高,但是過大的φ會導(dǎo)致系統(tǒng)抖振加劇,進(jìn)一步導(dǎo)致發(fā)散;γ應(yīng)該取一個相對較小的值,因為γ增大會使抖振賦值增大,但是太小的γ會導(dǎo)致系統(tǒng)控制精度下降;根據(jù)實際調(diào)試,參數(shù)如下:α1=50、β1=0.5、φ=10、γ=0.8、p1=5、q1=7。 4) 基于ANNFTSM的作動器系統(tǒng)參數(shù)設(shè)計原則如下:α、β、p、q的設(shè)計選擇參考快速終端滑模控制器,k2應(yīng)該取一個較小的值,較大會導(dǎo)致系統(tǒng)在發(fā)生故障時的振蕩加劇,但是過小會導(dǎo)致系統(tǒng)跟蹤響應(yīng)速度變慢;εs應(yīng)該取一個較小的值,εs過大會導(dǎo)致系統(tǒng)跟蹤響應(yīng)速度變慢,但是過小的εs會導(dǎo)致系統(tǒng)對故障的響應(yīng)速度減慢;神經(jīng)網(wǎng)絡(luò)自適應(yīng)率參數(shù)rw、rv應(yīng)該取一個較大的值,可以提高學(xué)習(xí)速率,但是過大會導(dǎo)致系統(tǒng)振蕩;神經(jīng)網(wǎng)絡(luò)層數(shù)過大會導(dǎo)致計算時間復(fù)雜度增加,導(dǎo)致系統(tǒng)響應(yīng)速度增加,故障發(fā)生時,過小的層數(shù)會導(dǎo)致系統(tǒng)無法及時跟蹤從而導(dǎo)致控制精度下降,根據(jù)實際調(diào)試,參數(shù)如下:α2=140、β2=2.3、εs=0.32、k2=0.01p2=4、q2=7、rw=0.2、rv=0.01,神經(jīng)網(wǎng)絡(luò)第2層結(jié)點數(shù)為111。 上述控制器各控制器都是在參數(shù)最優(yōu)的情況下進(jìn)行的。實驗中的3種工況的給定曲線為yd=(1-e-0.4t)sin(0.5t),如圖5所示。 圖5 給定曲線圖 正常情況下,系統(tǒng)只受到外界的干擾以及系統(tǒng)參數(shù)不確定性,不發(fā)生故障的情況,令收到的總擾動為f0=2x1x2(N·m)。 由圖6和表1所示,PID的平均值和標(biāo)準(zhǔn)差是最差的,ARC的平均值明顯低于FTSM和ANNFTSM,標(biāo)準(zhǔn)差略大于FTSM, PID和FTSM出現(xiàn)了比較明顯的抖振現(xiàn)象,雖然跟蹤誤差的平均值較低,但是標(biāo)準(zhǔn)差卻很大;ANNFTSM的跟蹤誤差的最大值、平均值和標(biāo)準(zhǔn)差都最小,這是因為ANNFSTM同時考慮了干擾和參數(shù)不確定性,在保證精度的同時,有效解決了FTSM抖振的問題。在響應(yīng)時間上看,ARC的響應(yīng)時間為10 s左右;PID、FTSM和ANNFTSM的響應(yīng)時間明顯快于ARC。正常情況ANNFTSM總擾動估計如圖7所示,神經(jīng)網(wǎng)絡(luò)觀測器主要觀測的是參數(shù)不確定性。 圖6 正常情況下各控制器跟蹤誤差圖 表1 正常情況下各控制器實驗跟蹤誤差效果統(tǒng)計 圖7 正常情況下ANNFTSM總擾動估計 滾珠絲杠間隙在t=20 s時因為摩擦力逐漸加大,檢測系統(tǒng)在發(fā)生緩變型故障時的響應(yīng)。 由圖8和表2可得,加上負(fù)載擾動f1后,PID、ARC和FTSM的控制精度明顯發(fā)生了大的偏差,F(xiàn)TSM相對于無故障情況,3個指標(biāo)已經(jīng)有了明顯的下降,ANNFTSM相對于無故障情況,控制效果幾乎沒有變化,只是在故障發(fā)生時有一個微小的突變,但是很快恢復(fù)到了正常水平,相對于其他3種控制器,該突變并不明顯,響應(yīng)速度方面,ARC明顯慢于FTSM和ANNFTSM。擾動為f1時ANNFTSM總擾動估計如圖9所示,ANNFTSM主要觀測的是f1和參數(shù)不確定行的總和。 圖8 擾動為f1時給定曲線和各控制器跟蹤誤差圖 表2 擾動為f1各控制器實驗跟蹤誤差效果統(tǒng)計 圖9 擾動為f1時ANNFTSM總擾動估計 在該干擾下會是使故障在t=20 s時突然發(fā)生,檢測系統(tǒng)在發(fā)生突變型故障時的響應(yīng)。 由圖10和表3可得,在發(fā)生賦值較大故障的時候,PID、ARC和FTSM控制精度相對于第2種情況有了一定程度的下降,同時變化的更快,ANNFTSM無明顯變化,只是在t=20 s的時候誤差曲線發(fā)生了一次突變,但是很快通過自身的故障調(diào)節(jié)機(jī)制又恢復(fù)了平衡,故障發(fā)生前和故障發(fā)生后的控制精度沒有明顯變化,且控制精度最高。負(fù)載擾動為f2時ANNFTSM總擾動估計如圖11所示,在故障發(fā)生時,同樣發(fā)生了一個一定幅值的抖動,但是很快又恢復(fù)正常,ANNFTSM主要觀測的是f2和參數(shù)不確定行的總和。 圖10 擾動為f2時給定曲線和各控制器跟蹤誤差圖 表3 擾動為f2時各控制器實驗跟蹤誤差效果統(tǒng)計 圖11 擾動為f2時ANNFTSM總擾動估計 加上故障以后,PID、ARC和 FTSM的誤差、平均值和標(biāo)準(zhǔn)差都有了比較明顯的下降,在有擾動的時候,F(xiàn)TSM的控制精度是明顯低于ANNFTSM,高于PID略高于ARC,由這個實驗得出,ANNFSTM的抗干擾能力及容錯能力更強,穩(wěn)定性也更好,在真實情況下控制精度也更高,響應(yīng)速度也明顯快于ARC。 1) 通過FTSM設(shè)計的航空機(jī)電作動器控制系統(tǒng)相對于PID和ARC有著更高的控制精度,響應(yīng)速度更快,為進(jìn)一步提高控制系統(tǒng)的穩(wěn)定性奠定了基礎(chǔ)。 2) 基于神經(jīng)網(wǎng)絡(luò)改進(jìn)的FTSM控制系統(tǒng)(ANNFTSM)通過觀測系統(tǒng)的參數(shù)誤差、外部干擾和可能發(fā)生的故障,并在控制器中進(jìn)行補償;同時,設(shè)計了非線性魯棒項克服神經(jīng)網(wǎng)絡(luò)的重構(gòu)誤差;實驗表明,相對于傳統(tǒng)的PID、非線性控制方法和一般的快速終端滑模而言,有更高的控制精度、更快的響應(yīng)速度、更強的抗干擾能力和容錯能力。 3) 通過對比實驗更好地驗證了控制器的有效性,對探索新型航空機(jī)電作動器的控制策略具有一定的參考價值。
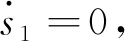
2.2 設(shè)計自適應(yīng)神經(jīng)網(wǎng)絡(luò)的快速終端滑模控制器(ANNFTSM)
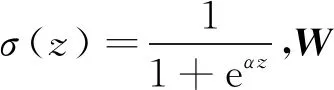

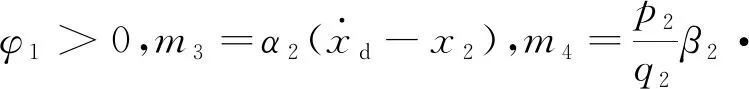
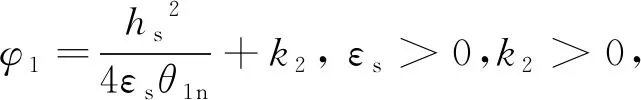
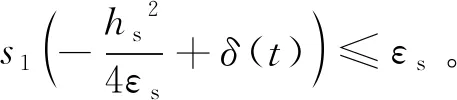
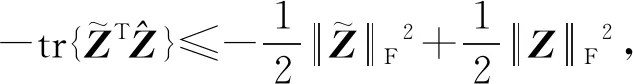
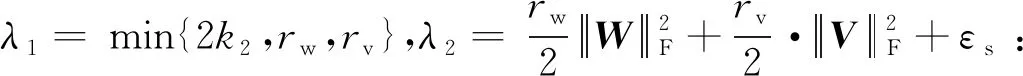

3 實驗結(jié)果

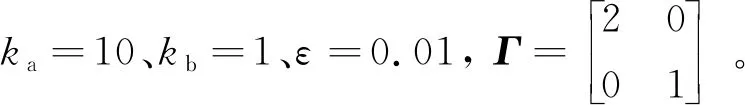
3.1 正常情況

3.2 擾動f1
3.3 擾動f2
4 結(jié) 論

