基于能量耗散的Q460焊接接頭S-N曲線快速預(yù)測
魏巍, 鄒麗, 楊鑫華
(1.大連交通大學(xué),遼寧 大連 116028;2.遼寧省軌道交通裝備焊接與可靠性重點(diǎn)實(shí)驗(yàn)室,遼寧 大連 116028)
0 前言
Q460耐候鋼由于強(qiáng)度高、耐候性好等優(yōu)點(diǎn),在鐵路貨車車體生產(chǎn)制造領(lǐng)域有廣泛的應(yīng)用。其焊接結(jié)構(gòu)在服役過程中承載著由車體產(chǎn)生的各類循環(huán)載荷,且因焊縫處的幾何、組織不連續(xù)性等特點(diǎn)[1-2],易于在焊趾處率先開裂而導(dǎo)致結(jié)構(gòu)疲勞破壞。因此,關(guān)于鐵路貨車Q460焊接結(jié)構(gòu)的疲勞壽命預(yù)測一直是業(yè)界關(guān)注的重點(diǎn)。焊接接頭疲勞壽命預(yù)測方法主要采用基于傳統(tǒng)疲勞試驗(yàn)測定的S-N曲線法[3]。這種方法試驗(yàn)周期長、所需樣本數(shù)量大及經(jīng)濟(jì)成本高,一直以來都是制約該方法應(yīng)用的主要因素。因此,如何發(fā)展一種基于小樣本疲勞試驗(yàn)數(shù)據(jù)快速測定S-N曲線的方法是業(yè)界關(guān)注的核心問題。
紅外熱像法具有實(shí)時(shí)、在線及非接觸等特點(diǎn),而被廣泛應(yīng)用于疲勞評估領(lǐng)域。在疲勞極限評估方面,F(xiàn)argion等人[4]和Luong等人[5-6]提出了采用基于穩(wěn)定溫升步長的雙線法疲勞極限預(yù)測模型,已被許多相關(guān)學(xué)者所證明[7-10]。樊俊鈴等人[11]發(fā)展了基于能量耗散的材料疲勞極限評估方法,揭示了疲勞溫升背后的不可逆能量耗散機(jī)理。在疲勞壽命預(yù)測領(lǐng)域,文獻(xiàn)[12]提出了基于熱像技術(shù)和能量耗散的點(diǎn)焊接頭疲勞壽命預(yù)測模型;Guo等人[13]提出了基于紅外熱像法的S-N曲線模型;Liu等人[14]建立了基于能量耗散的點(diǎn)焊接頭疲勞壽命預(yù)測模型。Li等人[15]研究了碳纖維復(fù)合材料試件的疲勞行為采用紅外熱像技術(shù),該方法將疲勞溫升三階段的循環(huán)周次占全部疲勞壽命的比例,作為疲勞壽命評估的依據(jù),為疲勞壽命評估提供了一種新思路。然而,盡管紅外熱像方法已經(jīng)在疲勞評估領(lǐng)域取得了較好的進(jìn)展。但是針對高周疲勞的研究較少,特別是針對焊接結(jié)構(gòu)的評估鮮少涉及。Huang等人[16-18]認(rèn)為對于高周疲勞而言,因疲勞過程中的滯彈性非常小以至于無法用設(shè)備監(jiān)測到,而高周疲勞過程又是一個(gè)累積損傷不斷增加的過程。
基于此,借助于紅外熱像技術(shù),以Q460對接接頭為研究對象,建立一種將焊接接頭疲勞壽命、疲勞極限及統(tǒng)計(jì)學(xué)結(jié)合起來的S-N曲線快速預(yù)測模型。模型以能量耗散為索引,通過計(jì)算得到不同載荷下的單位時(shí)間能量耗散值,確定隨載荷增加的能量耗散轉(zhuǎn)折點(diǎn),并以此進(jìn)行疲勞極限預(yù)測。然后,考慮當(dāng)載荷高于疲勞極限時(shí),其全壽命周期內(nèi)的能量耗散存在閥值,進(jìn)行中值S-N曲線預(yù)測評估,并結(jié)合統(tǒng)計(jì)學(xué)中的極大似然法快速預(yù)測P-S-N曲線。模型的優(yōu)勢在于僅需有限試件即可完成焊接接頭S-N曲線預(yù)測,且具有一定精度,為S-N曲線預(yù)測提供了一種新方法。
1 能量耗散理論基礎(chǔ)
能量耗散伴隨著高周疲勞過程,而這種能量耗散以試件標(biāo)距部分溫度逐漸升高的形式展現(xiàn)出來。結(jié)合熱力學(xué)第一定律和熱力學(xué)第二定律,試件標(biāo)距內(nèi)的局部熱平衡方程可以定義為公式(1)[7,13,19]:
ρCT-kdiv(gradT)=d1+sthe+sic+re
(1)
式中:ρ是材料密度;C是材料比熱容;T是實(shí)時(shí)溫度;k是熱導(dǎo)率;d1著材料的固有耗散,可表示為公式(2);sthe是熱彈性源,可表示為公式(3);sic暗示著由內(nèi)摩擦引起的熱源,可表示為公式(4);re是外部體積熱源。
d1=σ:D-ρψ,ε:ε-ρTψ,ε·α
(2)
sthe=ρTψ,T,ε:ε
(3)
sic=ρTψ,T,α·α
(4)
式中:σ是柯西應(yīng)力張量;D代表著歐拉應(yīng)變張量;ψ描述著亥姆霍茲自由能;ε是應(yīng)變張量;α代表著內(nèi)變量αj(j=1,2,…,n)。
根據(jù)文獻(xiàn)[7,13,16]的假設(shè),高周疲勞的固有耗散主要由兩部分引起:①不可逆微塑性變化;②可恢復(fù)的材料微結(jié)構(gòu)運(yùn)動(dòng)行為。對于第一部分而言,該部分能量耗散占據(jù)全部固有耗散的絕大多數(shù),且由該部分不可逆的微結(jié)構(gòu)變化引起的能量耗散,會(huì)導(dǎo)致試件出現(xiàn)不可逆的累積損傷增加;而對于第二部分而言(僅占全部固有耗散的很小部分),該部分可恢復(fù)的材料微觀結(jié)構(gòu)運(yùn)動(dòng)幾乎不會(huì)增加試件內(nèi)部的累積損傷。因此,就Q460焊接接頭的高周疲勞過程,一些假設(shè)可以總結(jié)為:①C和k是材料常數(shù),在高周疲勞過程中可以認(rèn)為是恒定的;②由sthe熱彈性源引起的溫度變化可以忽略;③由內(nèi)摩擦引起的熱源sic和外部體積熱源re可以忽略;④僅考慮沿焊縫縱向的溫度場分布。
基于以上假設(shè),試件標(biāo)距內(nèi)一維熱平衡方程可以表示為公式(5):
(5)
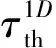
(6)
因此,高周疲勞過程中穩(wěn)定溫升階段單位周次內(nèi)的能量耗散可通過公式(6)計(jì)算得到。
2 三參數(shù)S-N曲線預(yù)測模型
2.1 疲勞極限預(yù)測
對于一個(gè)高周疲勞過程,其溫升進(jìn)程總體上可以分為3個(gè)階段,如圖1所示。①溫度迅速增加的第一階段;②溫升趨于穩(wěn)定的第二階段;③溫度瞬間升高的第三階段。
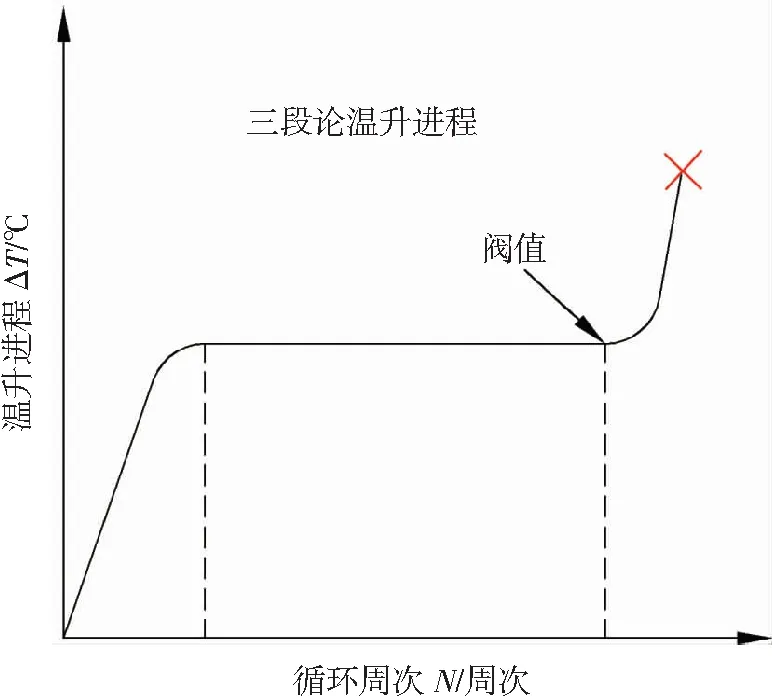
圖1 標(biāo)距部分疲勞溫升過程示意圖
Huang等人[8]在文獻(xiàn)中報(bào)道,隨著載荷(高于疲勞極限)的增加其穩(wěn)定溫升階段疲勞溫升值亦隨之增加,如圖2所示,并且隨著載荷的增加試件的壽命會(huì)逐漸減小。
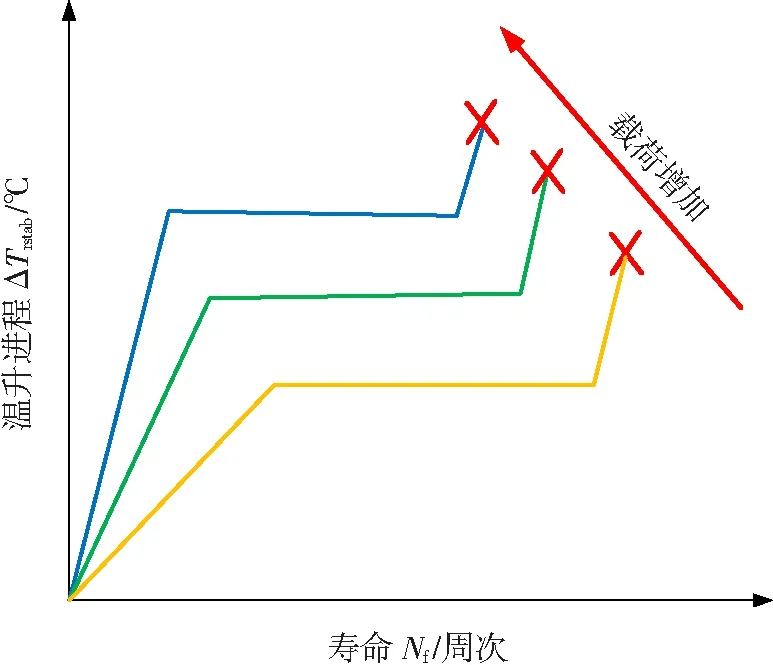
圖2 不同載荷下疲勞溫升進(jìn)程示意圖
鑒于上述內(nèi)容,結(jié)合Fargione等人[4]和Luong等人[5-6]提出的雙線法(如圖3所示),Huang等人通過計(jì)算不同載荷等級下ΔTrstab完成了對材料疲勞極限的準(zhǔn)確預(yù)測。但是,上述方法對于雙線法轉(zhuǎn)折點(diǎn)的確定僅基于視覺觀察,沒有確立一種基于數(shù)據(jù)的精確定位d1轉(zhuǎn)折點(diǎn)的方法。為精確定位d1轉(zhuǎn)折點(diǎn),將不同載荷下的數(shù)據(jù)點(diǎn)按照載荷從小到大的順序依次記為P1,P2,P3,…,Pi-1,Pi,Pi+1,…,Pn。然后,將相鄰2條線段Pi-1,Pi和Pi,Pi+1之間的斜率差(見公式(7))絕對值變化最大位置處所對應(yīng)的數(shù)據(jù)點(diǎn),作為d1隨載荷變化的轉(zhuǎn)折點(diǎn)。此后,將全部數(shù)據(jù)點(diǎn)分成2組,分別進(jìn)行線性擬合,將兩線交點(diǎn)所對應(yīng)的應(yīng)力幅值作為疲勞極限的預(yù)測值。
ΔSi-1,i,i+1=|Si,i+1-Si-1,i+1|(i≥2)
(7)
式中:ΔSi-1,i,i+1是相鄰2條線段斜率差的絕對值;Si,i+1和Si-1,i是相鄰2條線段的斜率值。因此,基于提出的方法可以迅速確定d1隨載荷變化的轉(zhuǎn)折點(diǎn),從而實(shí)現(xiàn)疲勞極限精確預(yù)測。
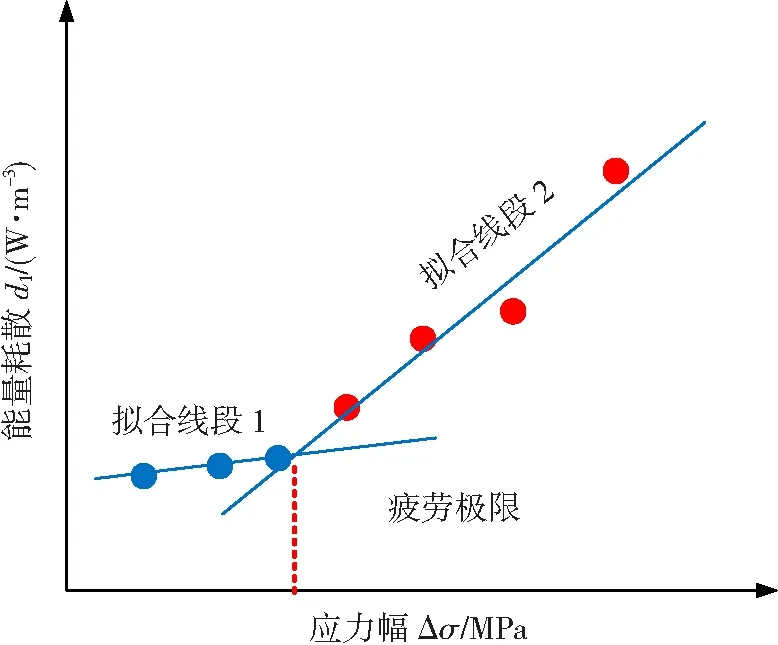
圖3 基于能量耗散的疲勞極限預(yù)測模型
2.2 S-N曲線預(yù)測
圖2中不同載荷下的疲勞溫升進(jìn)程呈現(xiàn)出2個(gè)基本特點(diǎn):①隨著載荷等級增加,試件的疲勞壽命趨于減小;②隨著載荷等級增加,試件的穩(wěn)定溫升步長ΔTrstab趨于增加。Crupi等人[9]認(rèn)為疲勞過程中存在能量閥值Ec,且該閥值可以表示為:
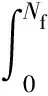
(8)
該模型僅是一個(gè)經(jīng)驗(yàn)性的模型,并未將能量耗散理論納入模型的建立當(dāng)中。因此,基于Huang等人[16-18]和Guo等人[13]提出的基本假設(shè),結(jié)合能量耗散模型(如1章節(jié)所述),從而實(shí)現(xiàn)Q460焊接接頭的疲勞壽命預(yù)測與評估。
根據(jù)文獻(xiàn)[7,8,10],當(dāng)載荷高于材料的疲勞極限時(shí),疲勞過程伴隨著不可逆的累積損傷增加;而當(dāng)載荷等級低于材料的疲勞極限時(shí),其疲勞過程可認(rèn)為幾乎是不存在損傷,即可認(rèn)為存在無限壽命(圖4)。因此,全壽命周期能量耗散閥值模型可定義為:
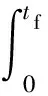
(9)
式中:Ec為能量閥值;Δd1為引起累積損傷的耗散值;tf是疲勞時(shí)間。因?yàn)榈诙厣A段占據(jù)約90%左右的疲勞壽命[13]。因此,公式(9)可以簡化為:
Ec={d1(2)-d1(1)}×tf
(10)
式中:d1(1)和d1(2)分別為為相應(yīng)應(yīng)力幅下的能量耗散值,且因tf×f=Nf,于是公式(10)可以變形為公式(11):
(11)
上式中d1(2)可以由公式(12)得到:
(12)
式中:a2為擬合直線2的斜率;d1(2)為相應(yīng)應(yīng)力幅下的單位周次能量耗散值;d1f為載荷達(dá)到疲勞極限時(shí)對應(yīng)的單位周次能量耗散值;Δσ為應(yīng)力幅(高于疲勞極限);Δσf為疲勞極限。
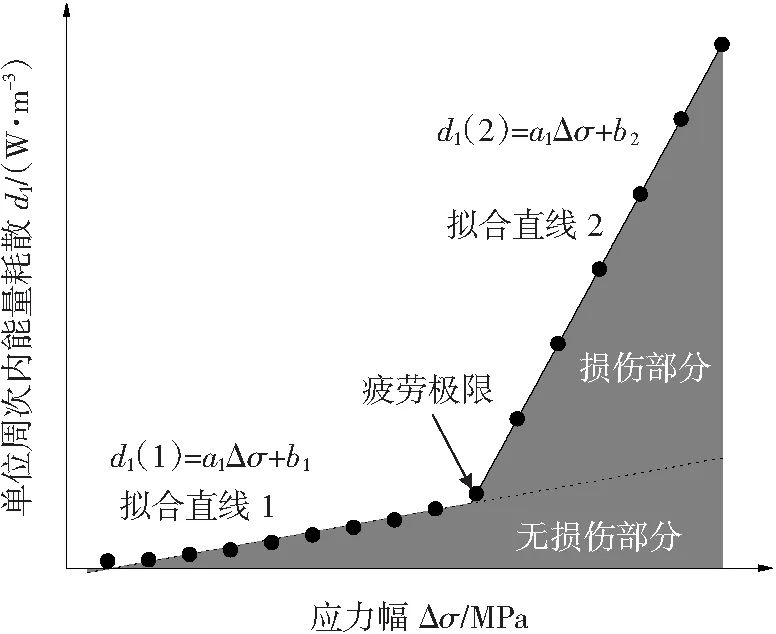
圖4 損傷模型示意圖
結(jié)合公式(11)和(12),當(dāng)載荷高于疲勞極限時(shí),能量耗散閥值模型可以表示為:
(13)
當(dāng)載荷接近疲勞極限時(shí),其穩(wěn)定溫升階段的能量耗散值非常小[20],因此d1f(2)-d1(1)可以認(rèn)為是忽略不計(jì)的,上式簡化為公式(14):
(14)
對于給定的應(yīng)力幅下,試件因其初始狀態(tài)的差異性從而導(dǎo)致疲勞壽命的分散性。因此,需對同一載荷下的能量耗散值進(jìn)行平均化處理,并將平均值作為能量耗散閥值的估計(jì)值。即:
(15)
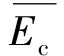
(16)
至此,一種基于能量耗散的三參數(shù)S-N曲線預(yù)測模型已經(jīng)建立,該模型可實(shí)現(xiàn)中值S-N曲線快速預(yù)測。然而,上述模型僅給出存活率為50%的S-N曲線預(yù)測方法,對于存活率為95%的S-N曲線可結(jié)合統(tǒng)計(jì)學(xué)中的極大似然法計(jì)算得到[21]。
3 試驗(yàn)方法
3.1 試驗(yàn)材料
采用板厚為8 mm的Q460對接接頭進(jìn)行疲勞試驗(yàn),采用MAG焊完成Q460對接接頭的焊接,保護(hù)氣體為80% Ar+20% CO2,坡口角度為55°,并對焊縫根部進(jìn)行打磨以消除其根部缺陷的影響。Q460試驗(yàn)材料化學(xué)成分與熱物理性能參數(shù)分別見表1和表2。

表1 Q460試驗(yàn)材料化學(xué)成分(質(zhì)量分?jǐn)?shù),%)

表2 Q460試驗(yàn)材料熱物理性能參數(shù)
3.2 疲勞試驗(yàn)
采用PLG-200高頻疲勞試驗(yàn)機(jī)進(jìn)行試驗(yàn),試驗(yàn)過程的載荷模式為單軸正弦循環(huán)波動(dòng)載荷,其試驗(yàn)頻率為125 Hz,應(yīng)力比為0.1。為保證試驗(yàn)穩(wěn)定進(jìn)行,需用緊固夾塊將試件兩端部夾緊。借助Fluke Ti450紅外熱像儀對試件標(biāo)距部分進(jìn)行實(shí)時(shí)溫度監(jiān)測,且為增強(qiáng)試件表面發(fā)射率,將黑色啞光漆均勻噴在試件(焊縫一側(cè))表面,試驗(yàn)相關(guān)裝置及設(shè)備如圖5所示。
結(jié)合第2章節(jié)所述模型,文中的疲勞試驗(yàn)可設(shè)計(jì)為:①采用應(yīng)力幅值為8個(gè)等級下的試件,每級載荷下各測試一個(gè)試件,至到其發(fā)生斷裂,將獲得疲勞壽命數(shù)據(jù)用于模型驗(yàn)證;②基于第1章節(jié)中的能量耗散模型,計(jì)算①中試件第二階段的單位周次內(nèi)的能量耗散,完成疲勞極限的預(yù)測;③完成疲勞極限預(yù)測后,在高于疲勞極限以上的任一應(yīng)力幅下再增加測試2個(gè)試件,得到該應(yīng)力幅值下平均能量閥值,然后基于公式(14)實(shí)現(xiàn)中值S-N曲線預(yù)測,結(jié)合極大似然法完成P-S-N曲線預(yù)測。
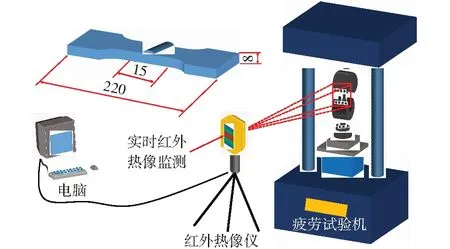
圖5 試驗(yàn)設(shè)備及裝置
4 試驗(yàn)結(jié)果
4.1 疲勞極限預(yù)測
如第2.1章節(jié)所述,一種基于能量耗散的精確測定材料疲勞極限模型已經(jīng)建立,該模型優(yōu)勢在于只需得到每一級應(yīng)力水平下的熱像數(shù)據(jù),即可完成材料疲勞極限的預(yù)測。因此,基于公式(7)可迅速確定d1轉(zhuǎn)折點(diǎn),從而完成不同載荷等級下能量耗散數(shù)據(jù)的分組,其疲勞極限預(yù)測結(jié)果如圖6所示。圖6中黃色菱形代表的是組1,藍(lán)色菱形代表的是組2(經(jīng)公式(6)計(jì)算得到當(dāng)ΔSi-1,i,i+1當(dāng)i=2時(shí)取得最大值)。擬合線1和擬合線2的R2分別為1和0.933 59,這表明其擬合程度較好,且擬合函數(shù)分別如公式(17)和公式(18)所示:
d1(1)=0.061 29Δσ-5.842 36
(17)
d1(2)=3.463 8Δσ-357.038 73
(18)
聯(lián)立公式(17)和公式(18),得疲勞極限值為103.216 9 MPa。然后,為驗(yàn)證該方法的有效性,將其與傳統(tǒng)的升降法結(jié)果進(jìn)行對比(見表3),結(jié)果表明二者誤差值僅為-1.35%,這暗示著熱像法可以實(shí)現(xiàn)快速且具有一定精度的疲勞極限預(yù)測。
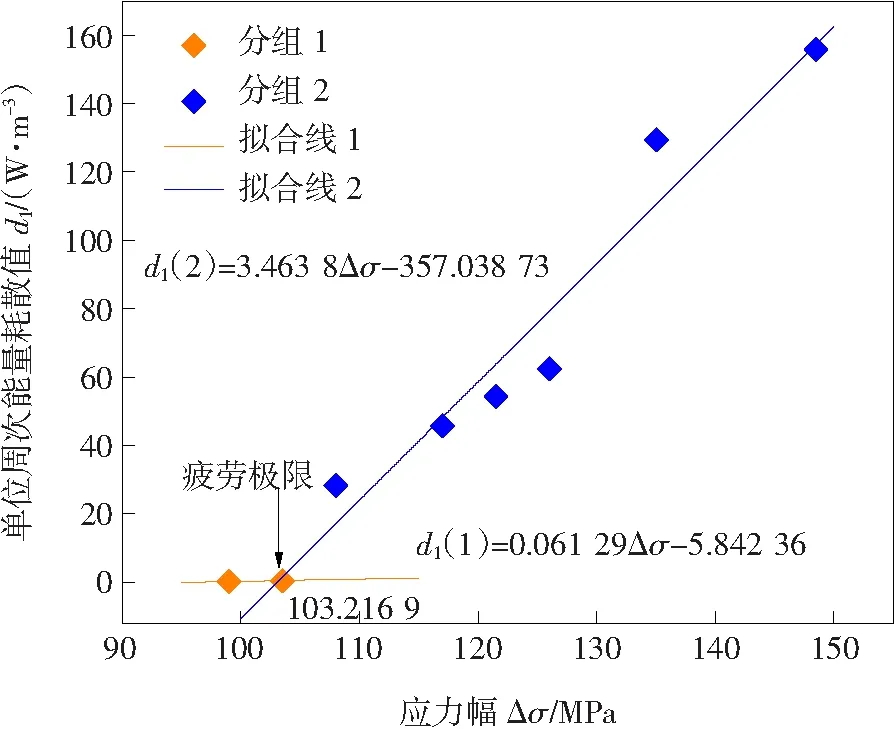
圖6 基于能量耗散的疲勞極限預(yù)測

表3 基于熱像法和升降法疲勞極限預(yù)測
4.2 S-N曲線評估
如第2.2章節(jié)所述,當(dāng)載荷等級高于疲勞極限時(shí),其累積損傷存在閥值,且該閥值可用于疲勞壽命預(yù)測模型建立,如公式(14)所示。然后,為實(shí)現(xiàn)快速預(yù)測不同存活率下的P-S-N曲線,結(jié)合第3.2章節(jié)中所述試驗(yàn)設(shè)計(jì)②,即在高于疲勞極限以上的某一應(yīng)力幅(這里取135 MPa),取3個(gè)試件的能量耗散值進(jìn)行平均處理,然后以此為閥值進(jìn)行P-S-N曲線預(yù)測。經(jīng)計(jì)算,3個(gè)載荷等級為135 MPa下試件疲勞全周期范圍的能量耗散見表4,故得平均能量耗散閥值為4.26×105W/m3。
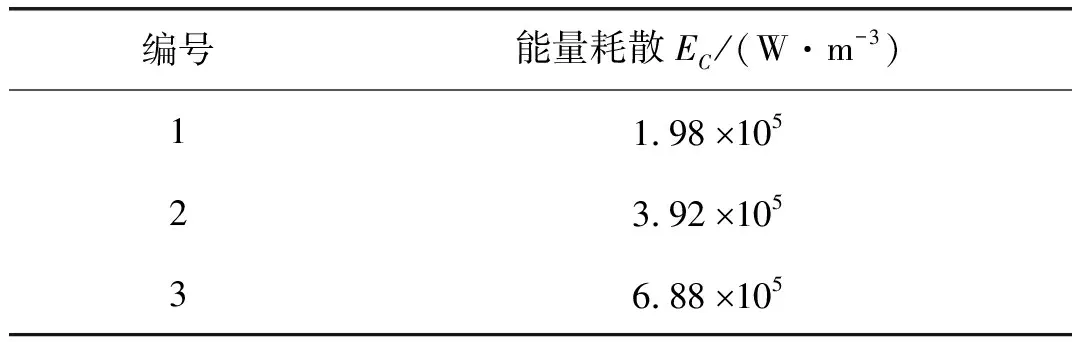
表4 應(yīng)力幅為135 MPa下的3個(gè)試件能量耗散
結(jié)合上述結(jié)果以及獲得的疲勞極限預(yù)測值,S-N曲線函數(shù)表達(dá)式可以寫為公式(19),該公式可用于預(yù)測存活率為50%的S-N曲線,然后,結(jié)合極大似然法完成了存活率為95%的S-N曲線評估,如圖7所示。
(Δσ-103.216 9)Nf=1.54×107
(19)
圖7為預(yù)測的S-N曲線與試驗(yàn)結(jié)果的對比,其中紅線代表的是存活率為50%的S-N曲線,黑線代表的是存活率為95%的S-N曲線,藍(lán)色空心圈代表的是試驗(yàn)數(shù)據(jù)。從圖7中可以看出,試驗(yàn)數(shù)據(jù)基本分布在存活率為50%的S-N曲線和存活率為95%的S-N曲線之間,這表明該利用提出第2.2章節(jié)提出的能量模型預(yù)測S-N曲線有著一定的精度,可以用于快速的S-N曲線預(yù)測以及疲勞壽命評估。
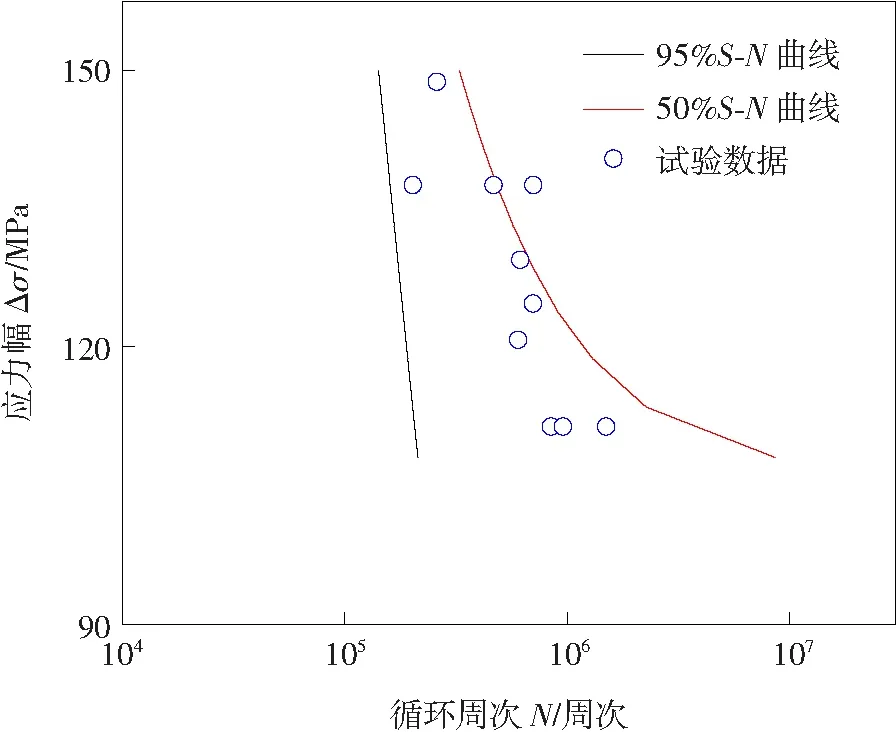
圖7 預(yù)測S-N曲線與試驗(yàn)數(shù)據(jù)對比
5 結(jié)論
建立了一種基于能量耗散的S-N曲線快速預(yù)測模型。首先,基于穩(wěn)定穩(wěn)定溫升階段的能量耗散轉(zhuǎn)折點(diǎn)實(shí)現(xiàn)了疲勞極限的精確預(yù)測。其次,借助于提出的基于能量耗散閥值理論的S-N曲線預(yù)測模型,完成了中值S-N曲線預(yù)測,并結(jié)合極大似然法得到了存活率為95%的S-N曲線。然后,將預(yù)測結(jié)果與試驗(yàn)結(jié)果對比,結(jié)果表明試驗(yàn)數(shù)據(jù)基本分布在50%曲線和存活率為95%的S-N曲線范圍內(nèi),從而驗(yàn)證了模型的精確性,這為以有限試件快速完成S-N曲線的設(shè)計(jì)提供了一種新方法。

