基于DNN改性瀝青中SBS含量的預(yù)測模型
王志祥, 李建閣
(1.長安大學(xué) 公路學(xué)院, 陜西 西安 710064; 2.廣東華路交通科技有限公司, 廣東 廣州 510420)
苯乙烯-丁二烯-苯乙烯嵌段共聚物(SBS)改性瀝青路面有效減少了車轍、坑槽、裂縫等早期病害的出現(xiàn)[1-2],增加了1~2 a使用壽命,提高了服務(wù)水平,因此SBS改性瀝青的研究及應(yīng)用備受青睞[3-4].SBS用量的劇增,導(dǎo)致了其價格上漲,以次充好、缺斤短兩的現(xiàn)象偶有發(fā)生,使改性瀝青中SBS的含量及其性能無法保證.傳統(tǒng)評價SBS含量的方法主要基于改性瀝青的儲存穩(wěn)定性,對其針入度、延度、軟化點和黏度等物理性能進行測試,但該測試方法耗時長、準確性和重現(xiàn)性較差[5-6];采用熒光顯微鏡定量檢測SBS含量,準確性較低[7];化學(xué)滴定方法雖然能夠測試改性瀝青中SBS的含量,但耗時長達2h,并且會釋放有毒氣體,危害試驗人員身體健康[8];通過傅里葉變換紅外光譜(FTIR)儀測定改性瀝青的紅外譜圖[9],基于特征峰與SBS含量的線性相關(guān)性,建立不同SBS含量改性瀝青標準曲線,可以測定改性瀝青中SBS的含量[10],但是其制樣的均勻性難以保證,紅外光譜峰的識別與提取、數(shù)據(jù)處理繁瑣且復(fù)雜,這給改性瀝青中SBS含量的測定帶來了困難[11].深度神經(jīng)網(wǎng)絡(luò)(DNN)在精準預(yù)測方面具有顯著優(yōu)勢[12].基于DNN,本文提出了改性瀝青中SBS含量的預(yù)測模型(DNN模型),旨在精準預(yù)測改性瀝青中SBS的含量,提升瀝青的質(zhì)量,改善瀝青路面的使用品質(zhì).
1 試驗
1.1 原材料
瀝青采用Shell-70#基質(zhì)瀝青(BA),其性能指標見表1.改性劑為韓國LG411星型SBS與LG501線型SBS的混合物,二者摻配比(1)文中涉及的比值、用量、含量等均為質(zhì)量比或質(zhì)量分數(shù).為1∶1;SBS顆粒色澤光亮,粒度均勻,雜質(zhì)含量較少,無明顯黏聚性,其性能指標見表2.根據(jù)工程經(jīng)驗,采用工業(yè)硫磺穩(wěn)定劑(用量為瀝青質(zhì)量的2‰)增強SBS與瀝青之間的黏聚力,確保改性瀝青的儲存穩(wěn)定性.
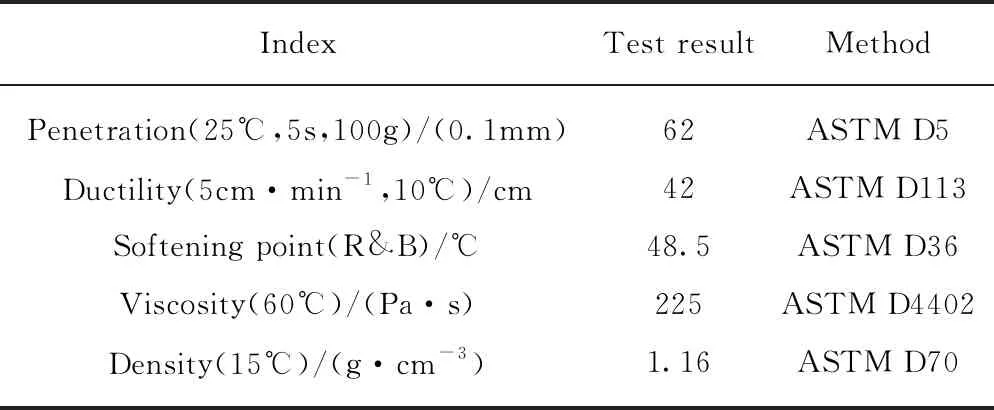
表1 基質(zhì)瀝青的性能指標
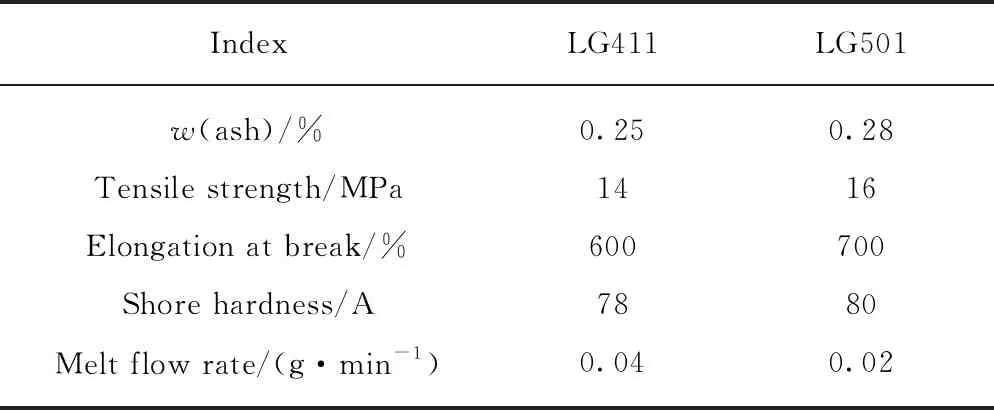
表2 SBS的性能指標
1.2 FTIR測試
采用配備ZnSe ATR附件的Controls Cary 630型FTIR,測試溫度控制在20℃左右,光譜范圍為4000~650cm-1,波數(shù)精度高于0.005cm-1,掃描次數(shù)為32次,分辨率為4cm-1.

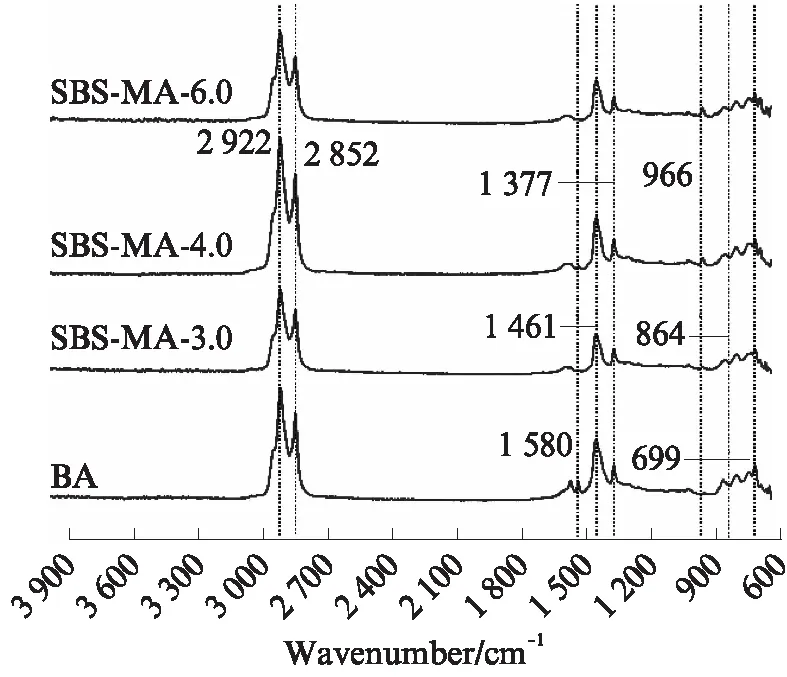
圖1 基質(zhì)瀝青及SBS改性瀝青的紅外光譜圖
2 DNN模型的建立
2.1 數(shù)據(jù)預(yù)處理
2.1.1降噪
制備7種SBS改性瀝青和1種基質(zhì)瀝青的FTIR測試樣品,每種樣品30個,共得到240個樣本.對其進行FTIR測試,得到240個FTIR圖譜特征數(shù)據(jù),并進行DNN訓(xùn)練與測試.FTIR圖譜采用Savitzky-Golay過濾器進行平滑預(yù)處理,減少噪聲干擾[14-15],同時對異常光譜進行剔除,得到227個有效FTIR圖譜.隨機抽取180個有效FTIR圖譜作為DNN訓(xùn)練樣本,樣本編號為1~180,剩余的47個有效FTIR圖譜作為DNN測試樣本,樣本編號為1~47.
2.1.2降維
每個FTIR圖譜均包含900個特征(維度),227個圖譜共有227×900個特征.采用奇異值分解算法對特征值數(shù)據(jù)的主成分進行降維,將輸入數(shù)據(jù)轉(zhuǎn)換成1組線性無關(guān)的特征值和相應(yīng)的特征向量[16].在保留能夠代表原始數(shù)據(jù)95%以上特征的前提下進行降維,最終得到227×512個特征數(shù)據(jù).
2.2 數(shù)據(jù)分類
將降噪+降維后的數(shù)據(jù)作為DNN訓(xùn)練和測試樣本的數(shù)據(jù)庫,其樣本信息見表3.表3中,N為數(shù)據(jù)預(yù)處理后的數(shù)據(jù)數(shù)量,Ntrain為用來訓(xùn)練的數(shù)據(jù)數(shù)量,Ntest為用來測試的數(shù)據(jù)數(shù)量.
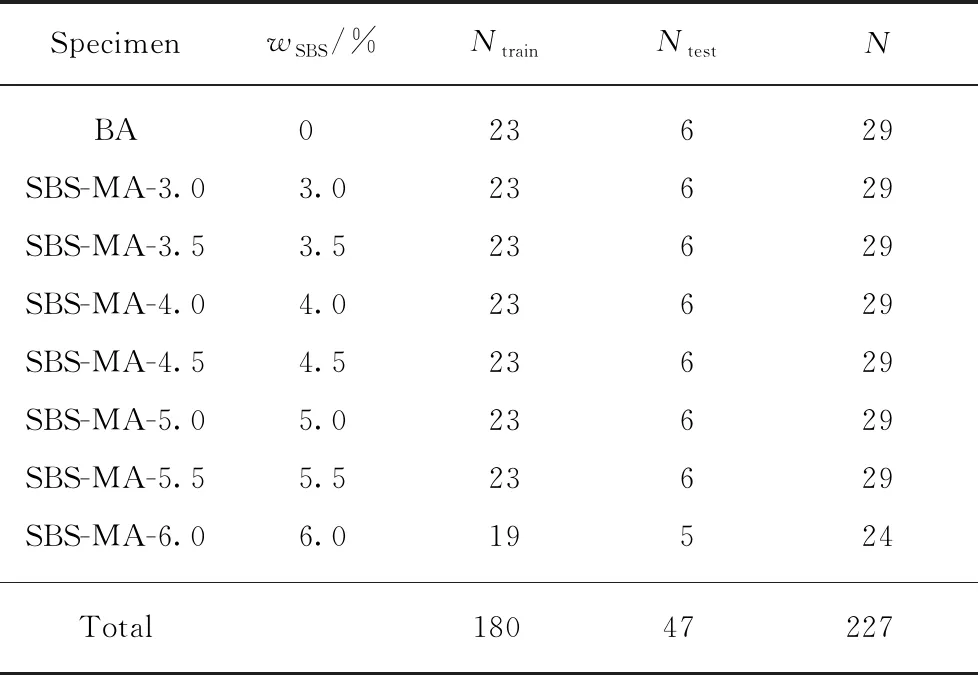
表3 數(shù)據(jù)庫樣本信息
2.3 DNN結(jié)構(gòu)設(shè)計
為保證神經(jīng)元直接快速并準確傳遞有效信息,對DNN結(jié)構(gòu)進行設(shè)計,建立的DNN結(jié)構(gòu)體系見圖2.由圖2可見:DNN由輸入層、輸出層和11個隱藏層組成,隱藏層從第2層到第12層依次排列,以提高學(xué)習(xí)的深度和模型表達能力;隱藏層神經(jīng)元節(jié)點數(shù)分別設(shè)置為512、256、256、128、128、64、64、32、32、16和16,以提高計算機的處理效率,加快優(yōu)化速度;同1層神經(jīng)元之間沒有聯(lián)系,但它們與下1個相鄰層的每個神經(jīng)元完全相連;將式(1)中SBS改性瀝青FTIR數(shù)據(jù)的特征向量X導(dǎo)入到包含512個神經(jīng)元的輸入層中;X(k)為X中的1個元素,為第k個樣本FTIR數(shù)據(jù)的特征向量,k=1,2,3,…,m,m為樣本數(shù);根據(jù)輸入值X,由式(3)計算得出SBS含量的輸出特征向量Y.
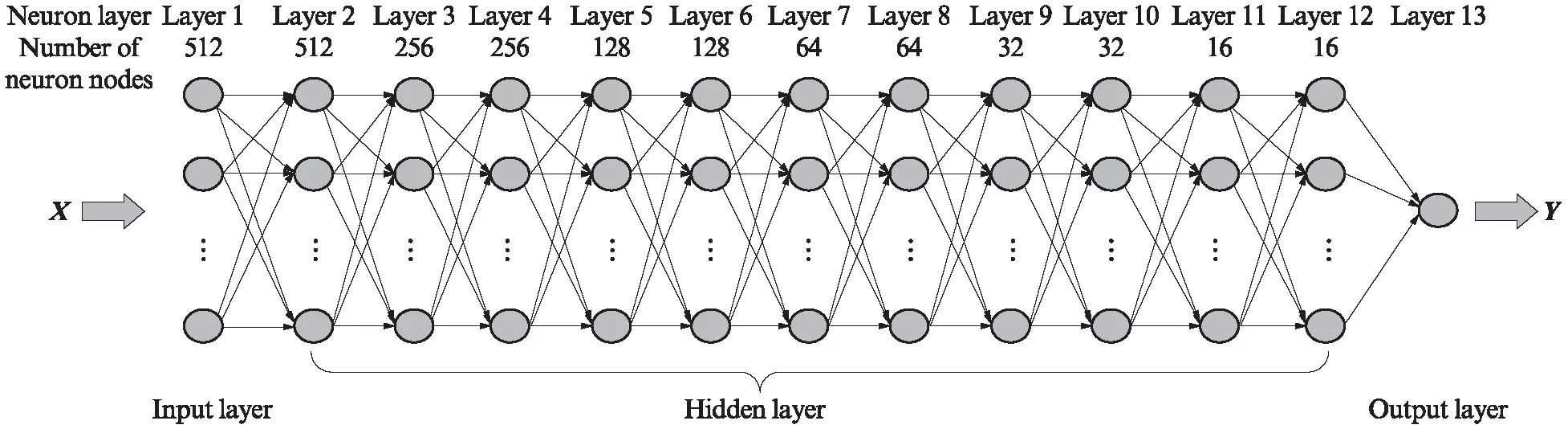
圖2 DNN結(jié)構(gòu)體系
X=(X(1),X(2),…,X(k),…,X(m))T
(1)
(2)
(3)
(4)
(5)
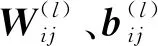
為避免在DNN的反向傳播過程中出現(xiàn)梯度消失現(xiàn)象,提高計算速度和精度,同時降低DNN參數(shù)的依賴性與過度擬合的概率,采用ReLU(梯度總是0或1)作為激活函數(shù)[17]:
f(x)=ReLU(x)=max(0,x)
(6)
式中:x表示輸入值;f(x)表示輸出值.
2.4 DNN訓(xùn)練
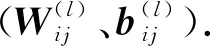
2.4.1損失函數(shù)
DNN訓(xùn)練通常采用損失函數(shù)J,使DNN模型輸出特征向量Y的預(yù)測值與事先已知的用來監(jiān)督預(yù)測模型的并和預(yù)測值相對應(yīng)的真實值y(目標值)無限接近.用均方誤差(MSE)作為損失函數(shù)J,并以MSE作為模型預(yù)測精度的評價指標,MSE值越小,模型預(yù)測精度越高.MSE的計算公式為:
(7)
2.4.2學(xué)習(xí)方法
學(xué)習(xí)在DNN訓(xùn)練中起著關(guān)鍵作用.學(xué)習(xí)過程為:首先將預(yù)處理后的數(shù)據(jù)以矩陣的形式輸入到DNN中,進行無監(jiān)督學(xué)習(xí),該過程為前向傳播中的特征學(xué)習(xí),權(quán)重和偏差特征向量的初始值用于訓(xùn)練第1層并生成用于訓(xùn)練第2層的特征向量數(shù)據(jù);依次利用產(chǎn)生的特征向量數(shù)據(jù)對下1層進行訓(xùn)練,直到最后1層完成訓(xùn)練后,得到各層相應(yīng)的權(quán)重和偏差特征向量數(shù)據(jù);最后對數(shù)據(jù)標記后進行監(jiān)督學(xué)習(xí),以調(diào)整DNN參數(shù)的權(quán)重和偏差特征向量.依據(jù)損失函數(shù),采用小批量隨機梯度下降法對每次迭代的參數(shù)進行更新,設(shè)置batch size為20,參數(shù)更新如式(8)、(9)所示.
(8)
(9)
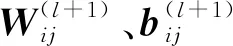
2.4.3初始化、規(guī)范化和歸一化
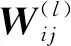
(10)
式中:ninput和noutput分別為輸入、輸出層連接的神經(jīng)元個數(shù).
為了降低DNN訓(xùn)練過程中過擬合出現(xiàn)的概率,常采dropout對DNN進行規(guī)范化,在每次迭代中,隨機隱藏一半的神經(jīng)元,在正向和反向傳播中,隱藏的神經(jīng)元都不會被激活.
通過批量歸一化,固定輸入層數(shù)據(jù),優(yōu)化求解過程,確保梯度穩(wěn)定,加快收斂速度和學(xué)習(xí)速度,防止梯度消失.特征向量X與矩陣特征值Z之間的關(guān)系為:
(11)
式中:μ、σ分別為特征向量X中批量數(shù)據(jù)的平均值和標準差;γ、β分別為由DNN訓(xùn)練得到的尺度因子和位移因子;ζ為平滑因子,為無窮小的數(shù)字,防止除數(shù)為零.
2.4.4DNN模型的效率
本文使用的計算機處理器為Inter(R)core(TM) i7-8700 CPU@3.20GHz,顯卡類型為Nvidia Geforce GTX 10708G GPU.通過CPU加速對DNN進行訓(xùn)練,前向傳播學(xué)習(xí)和后向反饋學(xué)習(xí)時間分別為8.22、25.37s.
2.5 DNN測試
DNN測試的目的是分析預(yù)測模型準確性.采用測試樣本進行DNN測試,若測試樣本的均方誤差小于訓(xùn)練樣本,說明模型預(yù)測準確性較好;否則,應(yīng)重新調(diào)整網(wǎng)絡(luò)結(jié)構(gòu)及其參數(shù),直至測試樣本的均方誤差小于訓(xùn)練樣本為止.
3 結(jié)果與討論
3.1 數(shù)據(jù)預(yù)處理對DNN模型預(yù)測精度的影響
其他條件相同,以MSE作為評價指標,研究了降噪+降維、僅降維、僅降噪3種數(shù)據(jù)預(yù)處理對DNN模型預(yù)測精度的影響,結(jié)果見表4.

表4 數(shù)據(jù)預(yù)處理對DNN模型預(yù)測精度的影響
由表4可見,對比沒有經(jīng)過數(shù)據(jù)預(yù)處理的DNN模型預(yù)測精度,僅降維預(yù)處理使MSE降低了6%左右,而僅降噪預(yù)處理使MSE降低了64%,降維+降噪預(yù)處理的綜合作用使MSE降低了70%,因此數(shù)據(jù)的降維、降噪等預(yù)處理對建立較為精確、魯棒性較好的預(yù)測模型有重要的作用.
3.2 迭代次數(shù)對DNN模型預(yù)測精度的影響
對訓(xùn)練樣本集設(shè)置不同的迭代次數(shù)(Nlit),研究其對模型預(yù)測精度的影響,結(jié)果見圖3.由圖3可見:隨著訓(xùn)練樣本集的迭代次數(shù)從100次增加到3000 次,DNN模型的MSE逐漸減小,從3.338減小到0.057;前1800次迭代,MSE波動較為明顯,單次的迭代不一定使神經(jīng)網(wǎng)絡(luò)向目標方向發(fā)展,但是整體趨向目標,通過反復(fù)迭代,調(diào)整權(quán)重和偏差,使網(wǎng)絡(luò)逐漸穩(wěn)定;當?shù)螖?shù)從1800次增加到2100 次,MSE緩慢下降,保持穩(wěn)定在0.057;當?shù)螖?shù)從2100次增加到3000次,MSE呈現(xiàn)小幅度波動.考慮訓(xùn)練速度,迭代次數(shù)選擇2100次.
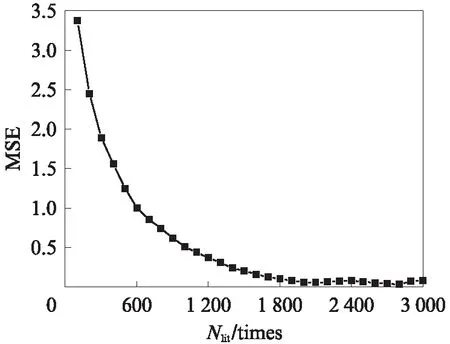
圖3 迭代次數(shù)對DNN模型預(yù)測精度的影響
3.3 DNN模型預(yù)測結(jié)果分析
對數(shù)據(jù)進行降維+降噪處理,迭代次數(shù)為2100次.訓(xùn)練樣本與測試樣本wSBS的預(yù)測值(PV)與目標值(TV)見圖4、5.由圖4可見:訓(xùn)練樣本的預(yù)測值在目標值附近小幅波動;樣本編號為100之前,預(yù)測值與目標值基本呈現(xiàn)正偏差狀態(tài);樣本編號在100之后,預(yù)測值與目標值出現(xiàn)負偏差,且呈小幅波動整體穩(wěn)定狀態(tài).由圖5可見:測試樣本的預(yù)測值在目標值附近小幅波動,wSBS的預(yù)測值穩(wěn)定在目標值附近.
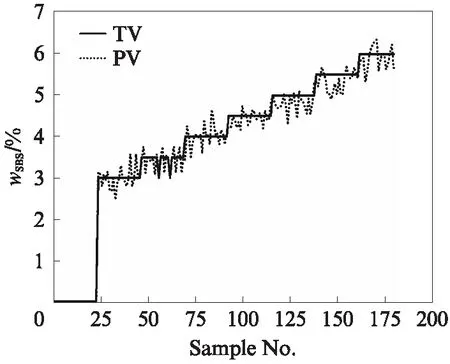
圖4 訓(xùn)練樣本的預(yù)測值與目標值
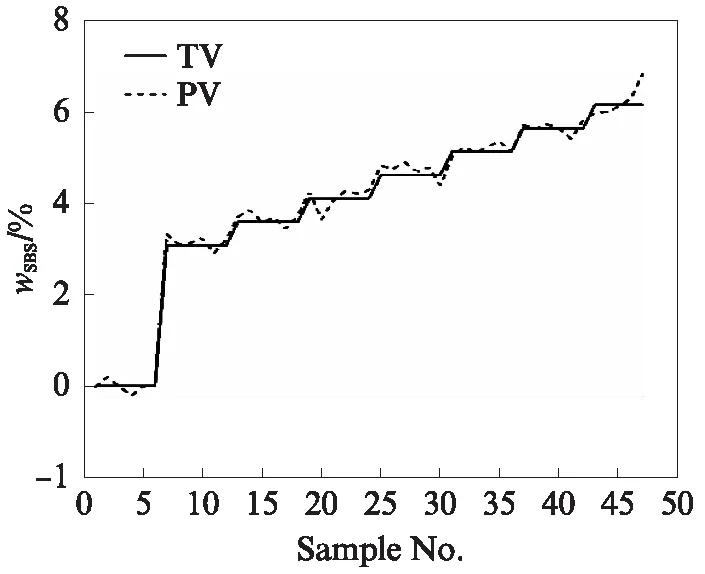
圖5 測試樣本的預(yù)測值與目標值
為進一步評價DNN模型的擬合優(yōu)度,將訓(xùn)練樣本集和測試樣本集中SBS改性瀝青的wSBS預(yù)測平均值與目標值進行相關(guān)性分析,結(jié)果見圖6.由圖6 可見,wSBS預(yù)測值的平均值與目標值相關(guān)系數(shù)R2達到0.9989,而測試樣本預(yù)測值的平均值與目標值相關(guān)性更好,R2達到0.9996,這也說明了DNN模型的準確性和適用性,通過預(yù)測平均值的計算,可以使預(yù)測值逼近目標值.
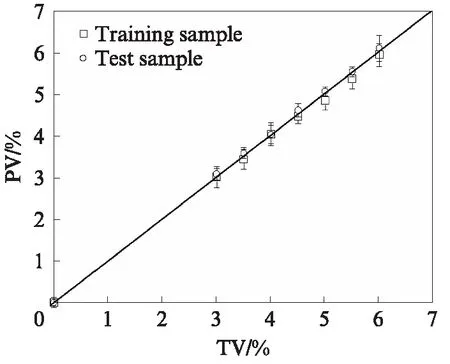
圖6 不同SBS含量的預(yù)測值的平均值與目標值的相關(guān)性分析
3.4 精度對比分析
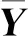
(12)
由表5可見:DNN模型的預(yù)測平均值與目標值線性相關(guān)系數(shù)R2為0.9989,模型預(yù)測精度優(yōu)于SCM和RFM模型;對于同一目標值wSBS=4.7%的樣本,RFM模型精度優(yōu)于SCM模型,而DNN模型具有更高的精度,達到98.756%.一方面,說明了DNN模型可以準確預(yù)測不局限于預(yù)測模型訓(xùn)練集中的wSBS(3.0%、3.5%、4.0%、4.5%、5.0%、5.5%、6.0%),且能預(yù)測wSBS為3.0%~6.0%區(qū)間任意含量值;另一方面,也說明了DNN模型的預(yù)測值更逼近目標值,wSBS目標值為4.3%、5.1%的樣本測試結(jié)果具有相同的結(jié)論;wSBS目標值4.3%、4.7%、5.1%的樣本測試精度中,wSBS=4.7%的樣本測試精度最高,測試結(jié)果最為精確.
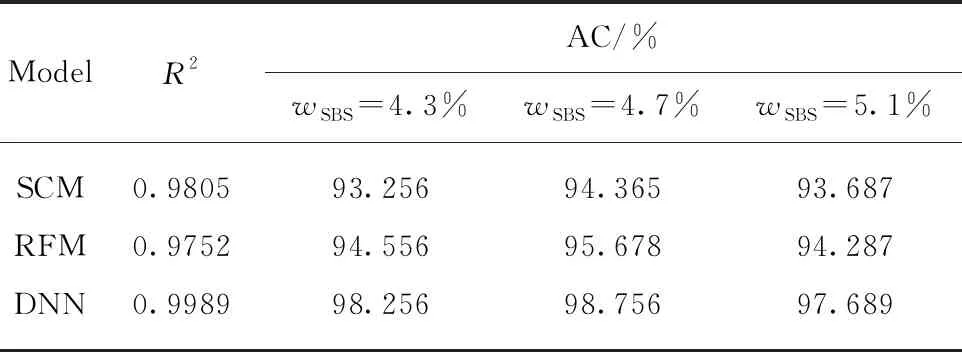
表5 3種預(yù)測模型預(yù)測精度比較
3.5 敏感性與適用性分析
為了驗證DNN模型的敏感性與適用性,選擇不同品牌和標號的基質(zhì)瀝青(Shell-70#、韓國SK-70#、新加坡IRPC-90#)、SBS(LG411、LG501、LCY3501、LCY3411)制備不同wSBS的SBS改性瀝青,按照本文所述方法測試其FTIR圖譜,同時用神經(jīng)網(wǎng)絡(luò)學(xué)習(xí)修正的DNN模型,對一定數(shù)量樣本的驗證集進行測定及精度評價,結(jié)果見表6.

表6 不同改性瀝青SBS含量結(jié)果
由表6可見:DNN模型能夠準確預(yù)測不同基質(zhì)瀝青和SBS改性瀝青中的SBS含量,且其預(yù)測值與目標值差值均在0.10%的范圍內(nèi),精度最低為97.78%,最高為98.75%.由此可見,DNN模型具有很好的敏感性和適用性,能用于準確預(yù)測不同種類的SBS改性瀝青中SBS含量.
4 結(jié)論
(1)在進行深度神經(jīng)網(wǎng)絡(luò)(DNN)訓(xùn)練之前,對數(shù)據(jù)進行降噪和降維等預(yù)處理,可以提高DNN模型的預(yù)測精度;相比于沒有進行數(shù)據(jù)預(yù)處理,經(jīng)過預(yù)處理的DNN模型的均方誤差MSE降低了70%.
(2)訓(xùn)練樣本集的MSE值最終保持在0.057,目標值與預(yù)測值接近,DNN模型具有良好的準確性.DNN模型對SBS改性瀝青中SBS含量的預(yù)測精度在97%以上,高于標準曲線法和隨機森林法.
(3)基于DNN改性瀝青中SBS含量預(yù)測模型對不同基質(zhì)瀝青與SBS改性瀝青中SBS含量預(yù)測具有較好的敏感性和適用性.

