化學強化鋁硅酸鹽玻璃表面微觀力學行為的有限元模擬

李曉宇，姜良寶，劉家希，王敏博，李佳明，顏 悅

(1 中國航發北京航空材料研究院，北京 100095；2 北京市先進運載系統結構透明件工程技術研究中心，北京 100095)

化學強化鋁硅酸鹽玻璃因其高強度、高硬度和良好的抗沖擊性能，廣泛應用于飛機、高鐵風擋及觸摸屏屏幕等領域[1-3]。化學強化，又稱離子交換，是熔融鹽液中半徑較大的堿金屬離子與玻璃表面半徑較小的堿金屬離子發生互擴散從而產生表面壓應力的過程。作為觸摸屏屏幕或飛機、高鐵風擋玻璃的主要材料，化學強化玻璃的表面抗損傷性能非常重要，表面硬度和模量與玻璃的抗損傷性能息息相關，通常作為評判化學強化玻璃抗損傷性能的關鍵指標。

納米壓痕方法是測量玻璃表面硬度和模量最為簡單有效的方式。采用納米壓痕方法研究材料的力學性能，需要準確理解材料的應力-應變曲線和壓痕加載-卸載曲線之間的關系[4]。納米壓痕過程中的很多參數，包括屈服應力、塑性變形區域、壓痕應力場分布狀態等均難以通過實驗獲得[5-6]，這些參數的分析方法主要有解析法和數值法兩類，而由于應力場的復雜性，解析法通常只能解決少量簡單問題，所以數值法已成為不可替代的廣泛應用的方法。有限元法就是伴隨著電子計算技術的進步發展起來的新興數值分析方法。利用有限元模擬能夠更好地理解納米壓痕過程中彈塑性變形及殘余應力場的變化[7]，并且能夠計算出一些難以通過實驗測量的塑性參數，例如脆性材料的屈服強度、塑性區域應力應變關系等[8]，對于研究脆性材料彈塑性變形行為、預測其力學性能具有重要科學意義。

采用有限元方法研究脆性材料在壓痕過程中的彈-塑性變形行為的報道很多[9-17]。描述壓痕應力場的模型中，最基本的兩個模型是Yoffe[9]模型和Chiang，Marshall，Evans的CME[10]模型。Yoffe通過無限彈性介質中心點擴張理論來獲得壓痕過程中的彈性應力。CME模型通過空洞擴張理論將塑性區域尺寸與材料力學參數聯系起來。后來，Laursen和Simo[11]在前人基礎上，采用有限元方法計算了壓痕過程中的應力場，指出有限元方法能夠獲得實驗難以獲得的多項參數。這些計算和模擬均基于壓頭為理想錐形的假設，即忽略了真實壓頭形狀對壓痕過程的影響。1994年，Giannakopoulos等[12]采用有限元方法模擬了金屬材料維氏壓頭的壓痕過程，考慮了真實壓頭的幾何形狀以及材料塑性區域應力應變關系對壓痕的影響，并計算了維氏壓頭壓痕過程中的應力分布。Larsson等[13]在1996年采用同樣的方法模擬了金屬材料玻氏壓頭的壓痕過程，并對玻氏壓頭壓痕過程中的力學理論基礎展開了深入的研究。Zeng等[14]根據Giannakopoulos和Larsson的模型，對多種性能差異很大的材料(包括金屬材料、脆性材料等)壓痕過程進行了有限元模擬，并與實驗結果進行對比，發現有限元能夠很好地模擬材料壓痕過程。Li等[15]采用有限元方法研究了石英玻璃在納米壓痕過程中致密化現象對其變形的影響。Kang等[16]采用有限元方法研究了玻璃表面殘余應力對納米壓痕過程中裂紋萌生及擴展過程的影響。

盡管針對硅酸鹽玻璃壓痕過程的有限元模擬研究成果很多，但這些研究大都集中于未經化學強化的原片硅酸鹽玻璃，對于經過化學強化后，表面具有壓應力層的硅酸鹽玻璃的壓痕過程研究很少。此外，采用浮法工藝生產的硅酸鹽玻璃由于下表面與錫液接觸會發生滲錫現象，造成浮法玻璃上下兩表面的成分和結構有所差異，通常稱之為空氣面和錫面，空氣面和錫面在納米壓痕加載-卸載過程中的表現有所差異，針對兩表面壓痕過程差異性的有限元模擬研究鮮見報道。

本工作以化學強化浮法鋁硅酸鹽玻璃作為研究對象，采用納米壓痕方法對化學強化鋁硅酸鹽玻璃加載-卸載過程中的力學行為展開實驗研究，并采用有限元方法對化學強化鋁硅酸鹽玻璃在納米壓痕實驗過程中的加載-卸載曲線進行分析，與實驗結果進行對照，同時采用有限元方法對納米壓痕實驗過程中無法獲得的玻璃應力-應變曲線、屈服應力、壓痕應力場等參數進行計算分析，為化學強化鋁硅酸鹽玻璃彈塑性變形行為研究提供理論依據。

1 實驗材料與方法

1.1 樣品制備

實驗采用2.2 mm厚的浮法鋁硅酸鹽玻璃樣品，其成分見表1。化學強化過程在離子交換爐(XFT-2500)中進行，采用純度大于99.9%的純硝酸鉀熔鹽進行強化。實驗樣品分兩組，其化學強化溫度分別為450 ℃和500 ℃，化學強化時間均為1 h。化學強化后采用錫面儀對每個樣品的“空氣面”和“錫面”進行區分及標記，并采用表面應力儀(FSM-6000LE)對樣品兩表面的表面壓應力(compressive stress，CS)和應力層深度進行測試(圖1)，表面壓應力和應力層深度測試結果見表2。

表1 玻璃樣品組分(質量分數/%)Table 1 Compositions of the glass samples(mass fraction/%)

圖1 表面壓應力和應力層深度測試Fig.1 Compressive stress and depth of stress layer testing

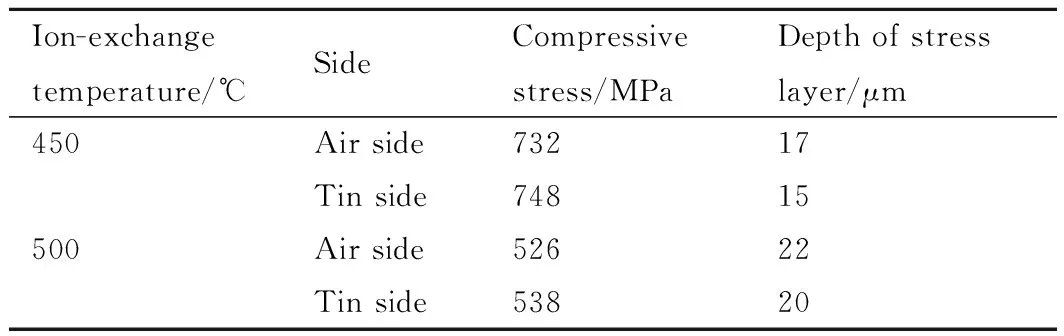
表2 表面壓應力和應力層深度測試結果Table 2 Results of compressive stress and depth of stress layer testing

1.2 納米壓痕實驗

納米壓痕采用Hysitron公司生產的原位納米力學測試系統(TI 950)進行，設備載荷最大量程為10 mN。壓痕實驗采用玻氏壓頭(Berkovich indenter)進行，圖2為典型納米壓痕形貌圖。每個樣品的“空氣面”和“錫面”均進行5次重復壓痕實驗，表面硬度和楊氏模量測試結果見表3。樣品的泊松比為0.25。

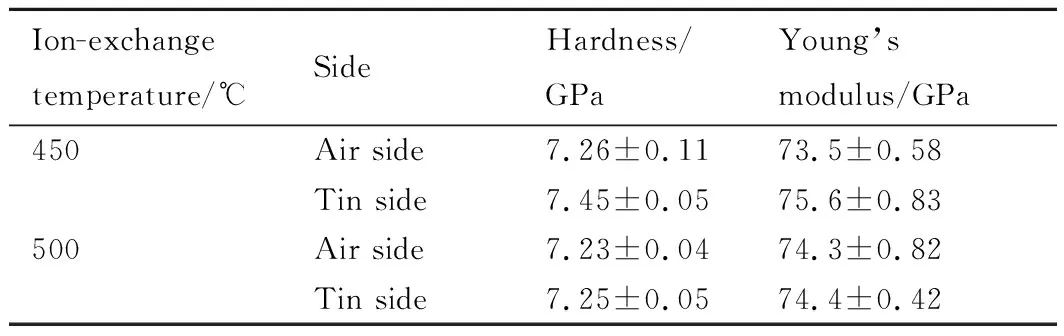
表3 表面硬度和楊氏模量測試結果Table 3 Results of hardness and Young’s modulus testing

圖2 典型納米壓痕形貌圖Fig.2 Typical image of nanoindentation

1.3 有限元模擬

納米壓痕的有限元模擬(FEM)有三維模擬和二維模擬兩種。據文獻報道[14-15]，三維有限元模擬在對裂紋萌生與發展的預測中具有不可替代的作用，而對于納米壓痕加載-卸載曲線的模擬結果與二維有限元模擬非常接近。由于本工作僅對納米壓痕加載-卸載曲線及相關參數進行研究，且二維有限元模擬計算量小、計算時間短，因此采用二維有限元進行模擬。模擬采用商業軟件ABAQUS 6.14進行。

1.3.1 建立模型

首先建立軸對稱二維有限元模型(圖3)，玻璃試樣尺寸設定為半徑100 μm，高100 μm的圓柱形試樣，該尺寸能夠保證模擬結果不受外邊界約束條件變化的影響。進行有限元分析時，選用線性軸對稱積分單元(CAX4)[18]對材料進行劃分，在單元尺寸發生改變的過渡區域采用多點約束方式定義[19]。圖3給出了典型的網格劃分示意圖。為了獲得精確的塑性變形和接觸面積，壓頭下變形區域的網格必須劃分得足夠細致，遠離壓頭區域的網格可以逐漸變疏，在保證精度的前提下減小計算量。同時，單元形狀盡量保持正方形或長寬比盡量小的矩形以確保精度，整個試樣由2940個四邊形單元組成。采用圓錐形壓頭，圓錐母線與中軸夾角φ=70.3°，以確保圓錐形壓頭與納米壓痕實驗采用的玻氏壓頭有相同的截面積-深度比。由于金剛石壓頭的硬度及楊氏模量比玻璃高出很多，模擬時將壓頭視為剛體。考慮到軸對稱情況，為減少計算量，僅對1/2模型進行模擬，設置邊界條件時，對稱軸上施加r方向位移約束，材料底部設置為不可變形，外邊界視為自由表面，邊界條件設置情況見圖4。壓頭與樣品之間視為無摩擦[20]，壓頭采用位移加載。

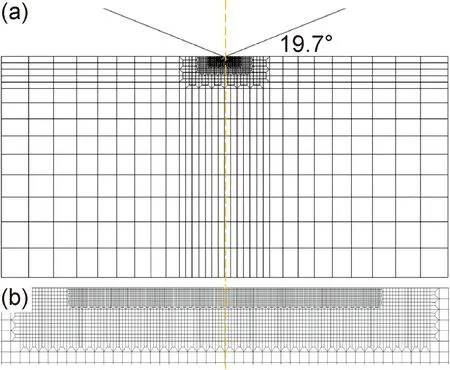
圖3 有限元網格劃分示意圖(a)整體網格；(b)接觸區域細分網格Fig.3 Schematic diagrams of finite element mesh(a)entire mesh；(b)details of the mesh in the region of contact

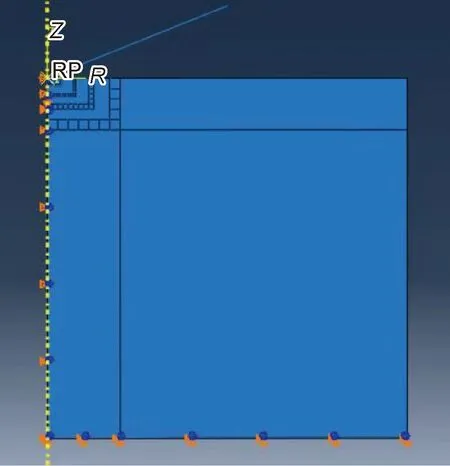
圖4 模型邊界條件設置情況Fig.4 Boundary condition of the model

1.3.2 玻璃塑性參數的計算

脆性材料在壓應力作用下開裂前存在彈性變形和塑性變形兩個階段[13]，因此，除彈性性質外，納米壓痕模擬過程中需輸入玻璃材料的塑性參數。模擬時玻璃材料屬性設定為均勻、各向同性，其應力-應變曲線選用雙線性模型[12]，認為玻璃在屈服前按照楊氏模量變化，屈服后的應力應變關系采用發生30%塑性應變時對應的應力(σr)來描述[12]，如圖5所示。

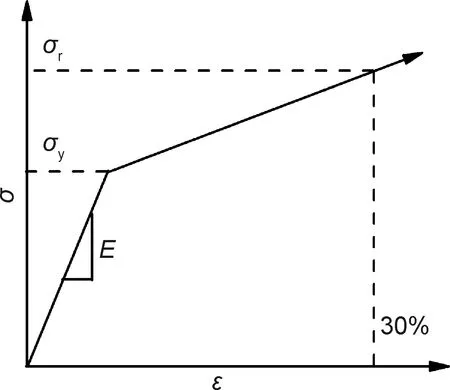
圖5 玻璃的應力-應變曲線Fig.5 Stress-strain curve of glass

其中，σ代表應力，ε代表應變。楊氏模量E由納米壓痕實驗獲得，泊松比υ取0.25。模擬采用的屈服準則為Von Mises屈服準則。對于陶瓷材料，通常認為屈服應力σy=0.48H(H代表硬度)[11-12]，因此根據納米壓痕實驗獲得的玻璃硬度值能夠得到玻璃的屈服應力。玻璃屈服之后的應力應變關系由參數決定。根據Larsson[10]給出的均勻、各向同性材料在玻氏壓頭下發生彈塑性變形時的解，壓痕過程中施加的載荷可以表達為式(1)：

(1)

式中：P為施加的載荷；h為壓入深度。

平均應力pav，即硬度，定義為施加的載荷與接觸面積之間的比值，可以由式(2)得到：

(2)

根據納米壓痕實驗得到的硬度、楊氏模量值，以及根據硬度計算出的屈服應力值，代入式(2)，即可獲得σr，將σy和σr作為玻璃材料的塑性參數輸入軟件中進行計算。

1.3.3 表面應力層的施加

化學強化玻璃表面壓應力層的模擬是通過施加預定義應力場實現的。圖6給出了施加預定義應力場后的應力情況示意圖,紅色部分代表化學強化玻璃的壓應力層。施加的預定義應力場深度為15 μm，與試樣真實應力層深度一致。由于壓入深度較淺(小于2 μm)，因此將應力場設定為均勻分布，不考慮應力隨深度的變化。

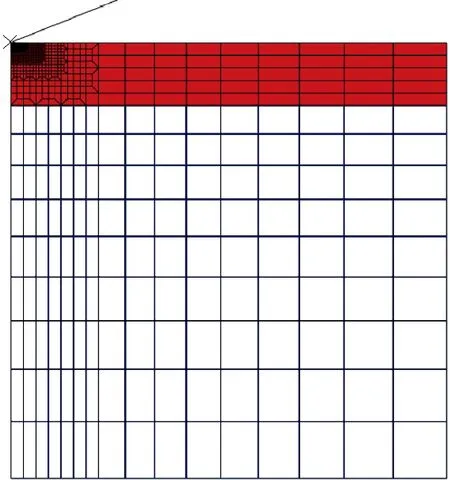
圖6 化學強化玻璃預定義應力場示意圖Fig.6 Schematic diagram of the pre-defined stress field for the ion-exchanged glass

1.3.4 硬度和楊氏模量的計算

有限元模擬輸出的結果包括加載和卸載過程的載荷-位移曲線、接觸面積及壓痕應力場等。根據獲得的載荷-位移曲線，采用Oliver-Pharr(OP)的方法，即可計算玻璃硬度和楊氏模量值。采用OP方法計算硬度和楊氏模量，需首先根據式(3)對卸載曲線進行指數擬合：

P=B(h-hf)m

(3)

式中：B和m為指數擬合參數；hf為完全卸載后獲得的壓痕殘余深度。

根據式(3)指數擬合得到的參數，代入式(4)，能夠得到材料的剛度S：

(4)

式中：hmax是最大壓入深度。壓頭與樣品之間的接觸深度hc可以通過式(5)得到：

(5)

式中：Pmax為最大壓入載荷；κ是依賴于壓頭幾何形狀的參數，對于玻氏壓頭，κ=0.75。

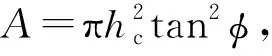
(6)

硬度和折合模量可以分別通過式(7)，(8)獲得：

(7)

(8)

折合模量與壓頭、樣品的楊氏模量、泊松比有關：

(9)

式中：E和υ為樣品的楊氏模量和泊松比；Ed和υd為金剛石壓頭的楊氏模量和泊松比。由于模擬過程中將壓頭視為剛體，即Ed=∞。因此，楊氏模量可以表達為：

(10)

根據式(5)～(10)，即可通過模擬獲得的載荷-位移曲線計算出材料的硬度和楊氏模量值。

2 結果與分析

2.1 屈服應力與載荷-位移曲線

模擬玻璃納米壓痕過程之前，首先需要根據納米壓痕實驗獲得的硬度值計算出玻璃的屈服應力。納米壓痕實驗得到的化學強化前原片玻璃空氣面硬度值為6.40 GPa，根據σy=0.48H的關系，可以得到原片玻璃空氣面的屈服應力為σy=3.07 GPa。同樣地，實驗得到的原片玻璃錫面硬度值為6.41 GPa，可以得到錫面屈服應力為σy=3.08 GPa。將玻璃空氣面的屈服應力σy=3.07 GPa，硬度H=pav=6.40 GPa，以及楊氏模量E=71.7 GPa值代入式(2)，即可獲得原片玻璃空氣面σr=8.41 GPa。同樣地，將玻璃錫面的屈服應力σy=3.08 GPa，硬度H=pav=6.41 GPa，以及楊氏模量E=72.7 GPa值代入式(2)，得到原片玻璃錫面σr=8.35 GPa。將計算得到的σy和σr值輸入ABAQUS軟件塑性參數中，即可對納米壓痕過程進行計算。

圖7對比了原片鋁硅酸鹽玻璃納米壓痕實驗獲得的載荷-位移曲線與有限元計算得到的載荷-位移曲線。從圖中可以看出，原片鋁硅酸鹽玻璃通過有限元獲得的載荷-位移曲線與實驗得到的載荷-位移曲線之間重合度非常好。有限元模擬采用的是位移加載，即位移為固定值。當壓頭壓入深度達到設定位移時，有限元計算得到的最大加載載荷與實驗設定的最大載荷之間相對誤差小于2%。影響有限元模擬結果的幾個重要的參數包括楊氏模量、泊松比、屈服應力和塑性區域應力應變關系(即σr)，分別輸入空氣面和錫面對應的參數后，兩個表面的有限元模擬結果都與實驗結果吻合度高。

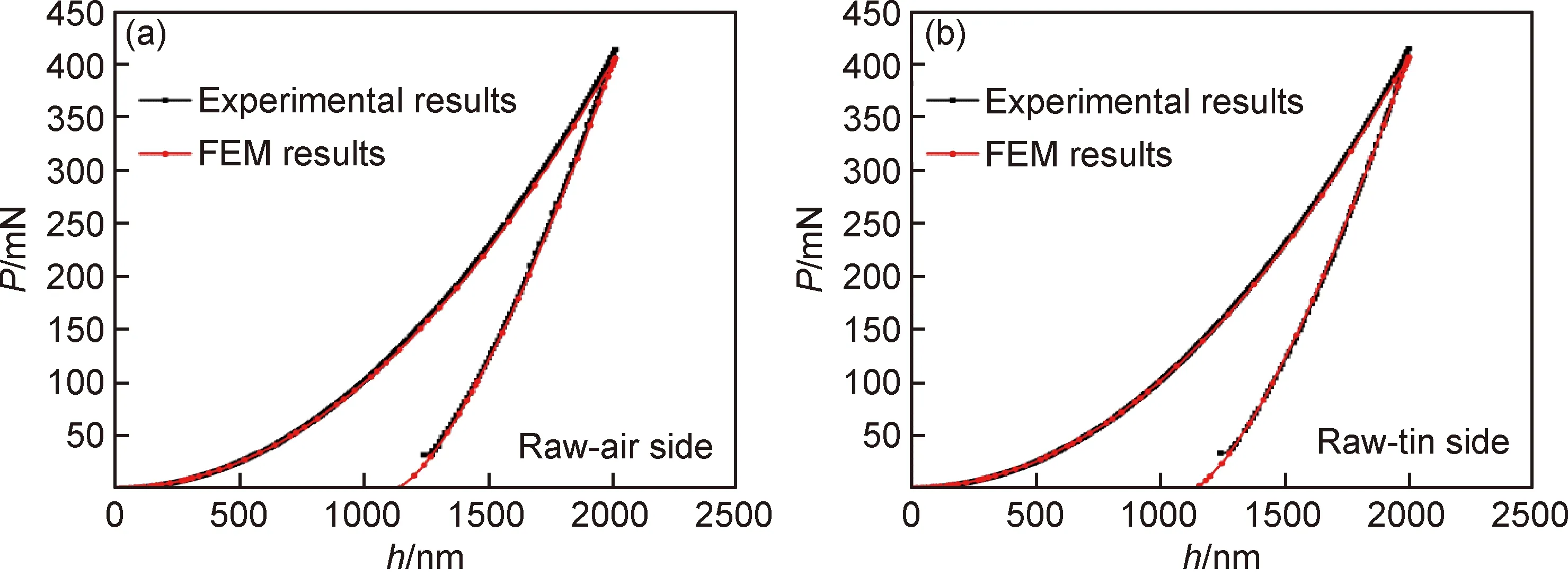
圖7 原片鋁硅酸鹽玻璃納米壓痕實驗與有限元計算得到的載荷-位移曲線的對比(a)空氣面;(b)錫面Fig.7 FEM calculated and experimentally measured indentation P-h curves for raw glass(a)air side;(b)tin side

有限元模擬得到的載荷-位移曲線與實驗得到的載荷-位移曲線的一致性說明有限元方法能夠準確模擬鋁硅酸鹽玻璃的納米壓痕過程，鋁硅酸鹽玻璃的彈塑性本構精確符合圖5的雙線性模型。同時，這一結果也說明通過式(2)計算得到的屈服應力及塑性區域應力應變關系與玻璃真實的塑性參數之間吻合度很高。脆性材料的塑性性質很難通過實驗獲得，有限元模擬可以用來驗證由理論計算得到的玻璃塑性參數的準確性。此外，計算得出的玻璃塑性參數與文獻報道[12]的結果十分接近，說明計算結果準確度較高。

圖8給出了具有不同表面壓應力的化學強化玻璃納米壓痕實驗與有限元模擬得到的載荷-位移曲線的對比。圖8(a)，(b)分別給出的是在450 ℃下強化1 h的化學強化玻璃空氣面和錫面的載荷-位移曲線，其表面壓應力分別為732 MPa和748 MPa。圖8(c)，(d)分別給出的是在500 ℃下強化1 h的化學強化玻璃空氣面和錫面的載荷-位移曲線，其表面壓應力分別為526 MPa 和538 MPa。采用施加預定義應力場的方法模擬出的化學強化玻璃載荷-位移曲線與實驗結果非常接近，當壓入同一深度時，有限元計算得到的最大載荷與實驗施加的最大載荷之間相對誤差小于2%，有限元計算結果能夠良好反應化學強化玻璃的納米壓痕過程。

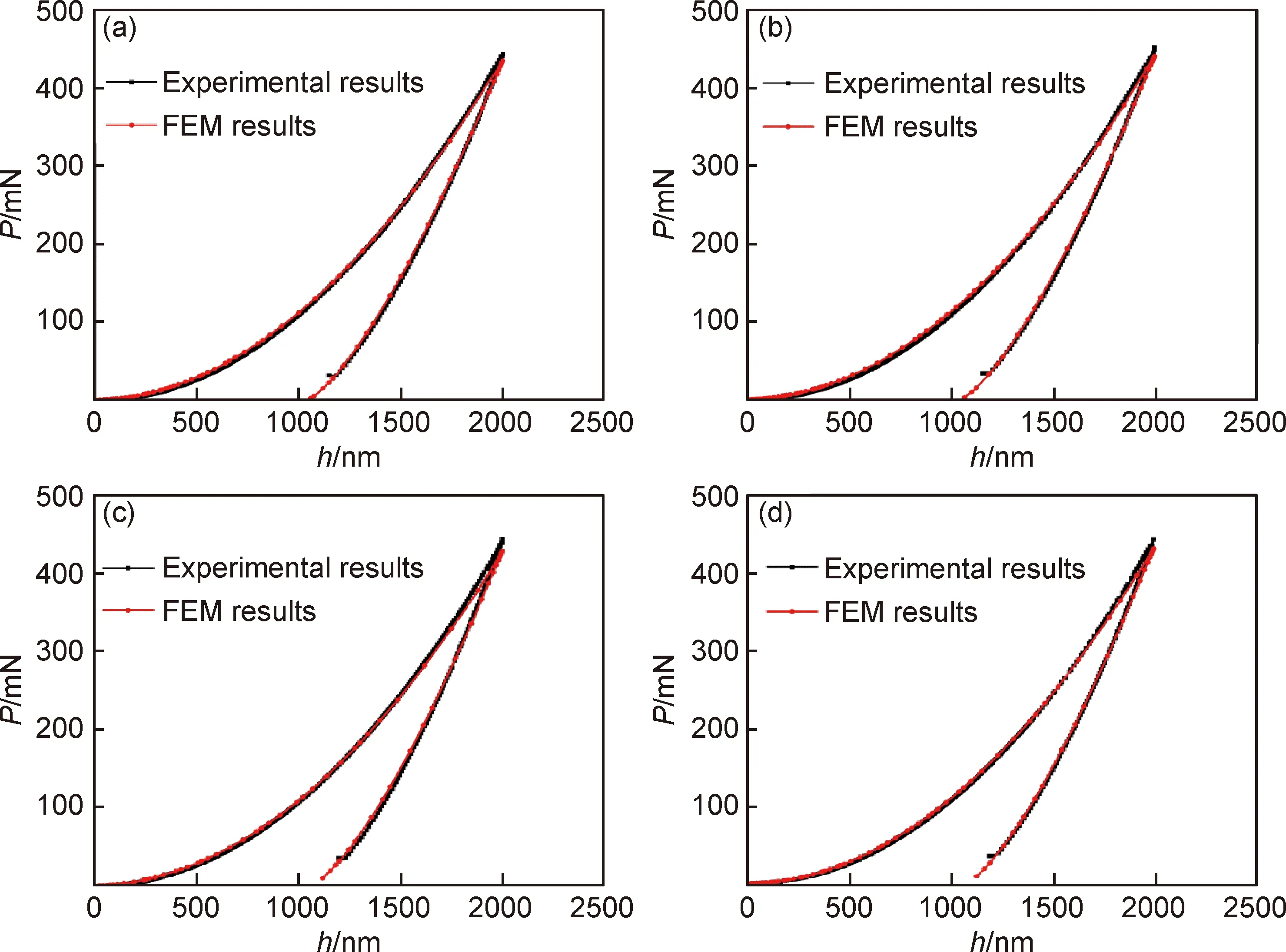
圖8 不同表面壓應力的化學強化鋁硅酸鹽玻璃納米壓痕實驗與有限元模擬計算得到的載荷-位移曲線的對比(a)732 MPa，空氣面；(b)748 MPa，錫面；(c)526 MPa，空氣面；(d)538 MPa，錫面Fig.8 FEM calculated and experimentally measured indentation P-h curves for ion-exchanged glass with different CS(a)732 MPa,air side;(b)748 MPa,tin side;(c)526 MPa,air side;(d)538 MPa,tin side

圖9對比了有限元模擬的原片玻璃和具有不同表面壓應力的化學強化玻璃的壓痕載荷-位移曲線。從圖中可以看出，當樣品表面存在預定義壓應力場時，載荷-位移曲線會產生明顯的變化。壓應力越大，壓入相同深度所需載荷越大，說明表面壓應力可以抵抗壓頭的壓入。這一計算結果與實驗結果一致。采用有限元方法能夠準確分析壓應力場對鋁硅酸鹽玻璃表面微觀力學行為的影響規律。

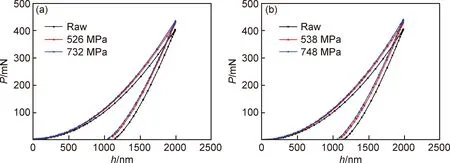
圖9 有限元獲得的原片玻璃與不同壓應力化學強化玻璃壓痕載荷-位移曲線(a)空氣面；(b)錫面Fig.9 Indentation load-displacement curves obtained from FEM for raw and ion-exchanged glasses with different CS(a)air side;(b)tin side

2.2 接觸面積

圖10給出了原片鋁硅酸鹽玻璃和具有不同表面壓應力的化學強化鋁硅酸鹽玻璃加載過程中壓頭接觸面積隨壓入深度的變化。從放大的插圖中可以看出，原片玻璃的接觸面積比化學強化玻璃的接觸面積大，接觸面積隨壓應力的增大而減小，這是因為玻璃表面大的殘余壓應力能夠抵抗壓頭的壓入造成的[21]。

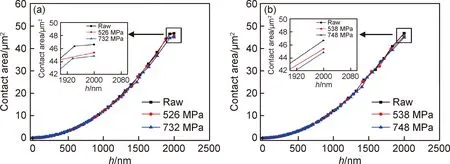
圖10 原片玻璃與具有不同表面壓應力的化學強化玻璃加載過程中接觸面積隨壓入深度的變化(插圖為最大壓入深度時接觸面積的放大圖) (a)空氣面；(b)錫面Fig.10 Variation of contact area with indentetion depth during loading of raw and ion-exchanged glasses with different CS (the insets are the enlargement of the final contact area)(a)air side;(b)tin side

2.3 硬度和楊氏模量

如2.1節中的結果所示，有限元模擬能夠精確描述原片玻璃與化學強化玻璃的壓痕載荷-位移曲線。根據有限元模擬得到的載荷-位移曲線，計算了玻璃的硬度和楊氏模量，并與實驗獲得的硬度、楊氏模量值進行了對比分析。

首先根據式(3)，對每一條有限元獲得的載荷-位移曲線的卸載曲線部分進行指數擬合，然后將獲得的指數擬合參數(B，m)及相關的壓入深度參數代入式(4)～(10)，即可得出不同玻璃樣品的硬度與楊氏模量值。不同樣品指數擬合參數及硬度、楊氏模量的計算結果見表4。指數參數m是描述卸載曲線形狀的一個重要參數，據文獻報道，大部分金屬和陶瓷材料在采用玻氏壓頭進行壓痕實驗時，其卸載曲線指數擬合獲得的參數m都在1.2～1.5范圍內變化[20]。從表4中可以看出，不同玻璃樣品的m值在1.22～1.37之間改變，與文獻報道一致，說明有限元分析結果與實驗結果吻合度較高。

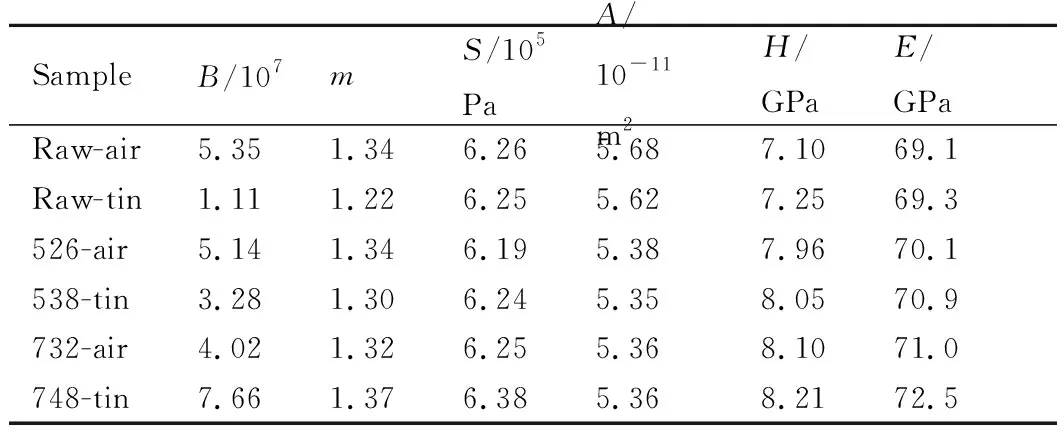
表4 有限元模擬的卸載曲線指數擬合參數及計算得到的硬度和楊氏模量值Table 4 Power law coefficients and calculated hardness and Young’s modulus results

為更好地對比根據有限元結果計算出的硬度、楊氏模量值與實驗得到的硬度、楊氏模量值之間的差異，圖11給出了不同壓應力的玻璃樣品模擬結果與實驗結果之間的比值。從圖11可以看出，對于不同壓應力的玻璃樣品，根據有限元結果計算出的硬度值與實驗得到的硬度值的相對誤差為10%，而根據有限元結果計算出的楊氏模量值與實驗值的相對誤差為2%。

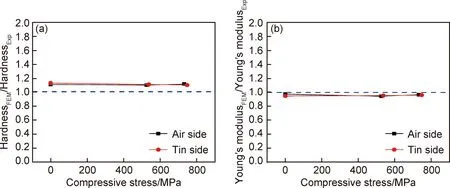
圖11 根據有限元結果計算的硬度值與實驗硬度的比值(a)和根據有限元結果計算的楊氏模量值與實驗楊氏模量的比值(b)隨壓應力的變化Fig.11 Ratio between hardness derived from the finite element results and from experimental results (a) and Young’s modulus derived from the finite element results and from experimental results (b) as a function of compressive stress

根據有限元模擬得到的載荷-位移曲線計算出的硬度值相比納米壓痕實驗得出的硬度值略微偏大，造成這一結果的主要原因在于實驗設備計算硬度時采用的接觸面積與根據有限元結果計算時采用的接觸面積不同。實驗設備采用的接觸面積是通過金剛石壓頭在標準熔融石英標樣上經過上百次壓痕實驗后，擬合得到的接觸面積關于壓入深度的經驗公式(如式(11)所示)，能夠更好地體現出壓頭的真實形狀，例如壓頭在使用過程中產生磨損，采用實驗方法能夠將磨損后的壓頭產生的真實接觸面積準確計算出來。然而有限元模擬采用的是理想圓錐壓頭，接觸面積是根據圓錐的幾何形狀計算出的理想接觸面積，理想圓錐壓頭在尖端處沒有曲率，相比實驗所用真實壓頭，必然會產生一個較小的接觸面積，導致計算得出的硬度值偏大。有限元計算得到的楊氏模量值與實驗值接近，略微偏小，產生這一偏差的原因在于壓痕設備在計算楊氏模量時采用的是真實金剛石楊氏模量和泊松比，而有限元模擬過程中假設壓頭是完全剛性的，即與被壓材料相比，壓頭楊氏模量視為無窮大，因此接觸面積的差異以及壓頭完全剛性的假設導致楊氏模量計算結果與實驗結果之間也存在一定偏差，但偏差非常小，說明有限元擬合結果能夠很好地預測鋁硅酸鹽玻璃的表面微觀力學性能。

(11)

2.4 壓痕截面及殘余應力場

圖12給出了原片玻璃和化學強化玻璃完全加載時的壓痕截面及Von Mises應力分布情況。納米壓痕過程中，被壓入材料易在壓痕周圍產生材料堆積現象(pile-up)。表面材料堆積會導致計算接觸面積時產生明顯的偏差，進而影響到硬度、楊氏模量計算結果的準確度。從圖12可以看出，原片玻璃和化學強化玻璃均沒有發生表面材料堆積現象。

研究壓痕過程中的應力分布狀態能夠更好地理解壓痕實驗中的物理現象。圖12反映了化學強化后殘余壓應力對壓痕過程中壓頭下方應力場的大小和分布的影響。對比原片及化學強化玻璃在完全加載時Von Mises應力可知，殘余壓應力對壓痕應力場的大小及分布狀態有顯著影響。Von Mises應力最大值出現在最接近壓頭下方的位置。從圖12(a),(b)可以看出，原片玻璃空氣面和錫面的Von Mises應力最大值分別為8.1 GPa和8.0 GPa，從圖12(c)～(f)中可以看出，化學強化后玻璃空氣面和錫面的Von Mises應力最大值增大至8.6～8.8 GPa之間。化學強化玻璃的表面殘余壓應力使得玻璃在壓痕過程中產生的Von Mises應力增大。此外，化學強化前后Von Mises應力分布狀態也有較大改變。據文獻報道，接近壓頭下方的近場Mises應力與材料的塑性區域相關[14]。對比原片玻璃與化學強化玻璃的近場應力，發現二者區別很小，說明化學強化對玻璃的塑性區影響較小。然而兩種玻璃樣品的遠場應力分布區別十分明顯，化學強化玻璃的遠場Mises應力比原片玻璃更局限于表面壓應力層深度范圍內，而在水平方向上影響區域更廣。遠場Mises應力與材料彈性區域相關[19]，化學強化玻璃遠場Mises應力與原片玻璃的差異說明化學強化對玻璃的彈性區影響較大[22]。研究表明，當化學強化玻璃發生反向離子交換使得玻璃表面離子恢復原有狀態時，玻璃的體積會完全恢復至離子交換前[22]，說明化學強化的離子交換過程引入的應變是彈性應變。根據脆性材料壓入理論，壓痕過程可以分為3個明確的階段：全彈性、彈塑性和全塑性。當壓入載荷很小時，玻璃發生彈性變形，隨著壓入載荷的增大，逐漸由彈性變形轉變為塑性變形。前期作者在研究化學強化鋁硅酸鹽玻璃在加載損傷過程的彈/塑性變形行為時，發現化學強化鋁硅酸鹽玻璃發生彈/塑性變形轉變的臨界載荷高于原片鋁硅酸鹽玻璃，同樣證明化學強化玻璃能夠在更大的載荷范圍內發生彈性應變[3]，這些研究成果與有限元模擬的結果是一致的。

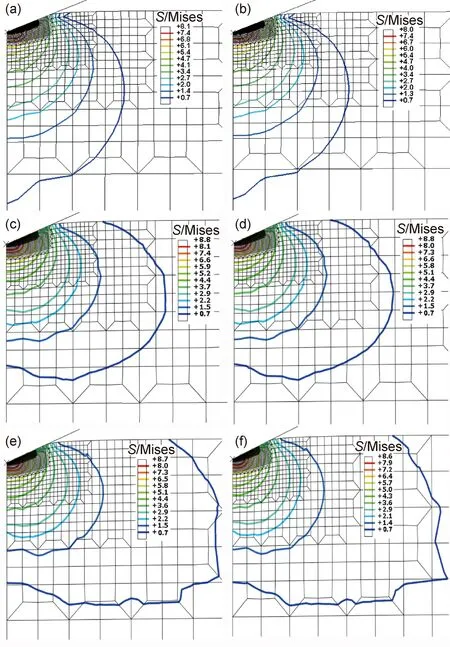
圖12 原片玻璃和化學強化玻璃完全加載時Von Mises應力分布情況(a)原片玻璃，空氣面；(b)原片玻璃，錫面；(c)526 MPa，空氣面；(d)538 MPa，錫面；(e)732 MPa，空氣面；(f)748 MPa，錫面Fig.12 Von Mises stress distributions at fully loaded of raw and ion-exchanged glasses(a)raw glass,air side;(b)raw glass,tin side;(c)526 MPa,air side;(d)538 MPa,tin side;(e)732 MPa,air side;(f)748 MPa,tin side

3 結論

(1)采用Larsson塑性公式計算得出的玻璃屈服應力及塑性區域應力應變關系進行有限元模擬得到的壓痕載荷-位移曲線與實驗結果吻合度高，有限元方法能夠準確模擬化學強化鋁硅酸鹽玻璃的納米壓痕實驗過程。

(2)壓入深度相同時，化學強化鋁硅酸鹽玻璃相比原片鋁硅酸鹽玻璃的壓入載荷較大，而接觸面積較小。

(3)根據有限元模擬得到的載荷-位移曲線，采用Oliver-Pharr方法計算得到的硬度值與實驗得到的硬度值的相對誤差為10%，楊氏模量的相對誤差為2%，表明采用有限元方法能夠較好地預測樣品的硬度和楊氏模量。

(4)有限元給出的Von Mises應力分布說明化學強化對鋁硅酸鹽玻璃的彈性區影響較大，對塑性區影響較小。