基于五階WENO格式的燃?xì)庠谒幋仓辛鲃舆^程二維兩相流研究*
程申申,王 浩,薛 紹,陶如意
(南京理工大學(xué)能源與動力工程學(xué)院,江蘇 南京 210094)
膛內(nèi)點(diǎn)傳火過程是一個復(fù)雜的高溫高壓傳熱傳質(zhì)過程,包括點(diǎn)火管火藥燃燒、點(diǎn)火管燃?xì)饬鞒鲆约疤艃?nèi)藥床的傳熱燃燒過程,對火炮的藥床燃燒以及后續(xù)推進(jìn)過程有重要的影響。在實際實驗中,現(xiàn)有測試手段很難得到實際狀態(tài)下這一階段的實驗現(xiàn)象。因此,開展藥床燃?xì)饬鲃拥膬?nèi)彈道模擬對整個火炮發(fā)射過程的研究具有重要意義[1-3]。
近年來針對點(diǎn)火管和膛內(nèi)火藥床燃燒的研究成果有很多。王浩等[4]通過點(diǎn)傳火特性實驗,對比了不同裝填條件下的傳火管多點(diǎn)壓力曲線及火焰?zhèn)鞑ニ俾剩治隽说谆鹧嬖趥骰鸸苤械膫鬏斕匦裕窃缙趯c(diǎn)傳火進(jìn)行的實驗研究。王珊珊等[5-6]對點(diǎn)火管和中心管建立了一維兩相流模型進(jìn)行內(nèi)彈道兩相流研究,分析了不同結(jié)構(gòu)點(diǎn)火管的點(diǎn)傳火性能。郭夢婷等[7]對中心炸管定容階段進(jìn)行了二維兩相流研究,探究了中心管式拋撒機(jī)構(gòu)的內(nèi)彈道流場特性。但是以上研究都著眼于點(diǎn)火管內(nèi)火藥燃燒和傳播,對于燃?xì)庠谔艃?nèi)流動及火藥燃燒的研究較少。Miura 等[8]使用帶破裂膜片的燃燒裝置進(jìn)行實驗,并采用兩相流體動力學(xué)代碼進(jìn)行模擬計算,用于探索膛內(nèi)負(fù)壓差產(chǎn)生的機(jī)理,并得出結(jié)論,壓差是由固體推進(jìn)劑運(yùn)動導(dǎo)致的,壓差波動取決于底火噴口的流量和噴口的位置,但實驗和模擬過程未對火焰發(fā)展及流場規(guī)律進(jìn)行詳細(xì)描述和觀測。Jaramaz 等[9]對整個火炮膛內(nèi)流動過程進(jìn)行實驗和一維兩相流研究,但是未考慮徑向效應(yīng)。程誠等對某制導(dǎo)炮彈二維兩相流內(nèi)彈道性能進(jìn)行研究,并采用高階黎曼近似模型求解兩相流方程,詳細(xì)研究了帶推進(jìn)系統(tǒng)的整個內(nèi)彈道過程中膛內(nèi)流場特性及其發(fā)展[10-11],但主要研究火藥床燃燒及彈丸推進(jìn)過程,并未仔細(xì)對初始階段點(diǎn)傳火過程進(jìn)行流場分析。因此,開展中心傳火管裝藥點(diǎn)火過程的理論與試驗研究,對進(jìn)一步分析火炮發(fā)射起始階段膛內(nèi)的點(diǎn)火過程燃?xì)饬鲃右?guī)律,降低起始壓力波的產(chǎn)生,保證火炮射擊的安全性至關(guān)重要。
本文中,擬設(shè)計低壓可視化實驗裝置,觀察點(diǎn)火藥燃?xì)庠谒幋仓械牧鲃舆^程。考慮到可視化裝置的承壓能力,采用假藥粒裝填結(jié)構(gòu),并結(jié)合二維兩相流數(shù)值模擬來預(yù)測這一階段的實際過程。使用五階精度的WENO格式,相比于經(jīng)典的Mac Cormack 格式與TVD格式,其具有精度高、間斷分辨清晰,而且效率高的優(yōu)點(diǎn),是十分有效的算法[12-14]。以期研究結(jié)果對進(jìn)一步開展火炮起始階段燃?xì)饬鲃蛹皦毫ψ兓?guī)律研究具有應(yīng)用價值。
1 數(shù)理模型
1.1 物理模型
對膛內(nèi)初始階段點(diǎn)傳火過程建立的計算模型如圖1所示。膛內(nèi)填充由尼龍材料仿真實藥粒大小制成的假藥粒,中心為點(diǎn)傳火管,內(nèi)裝小粒黑火藥,左端用端蓋密封,裝有底火以點(diǎn)燃點(diǎn)火管內(nèi)火藥,右端用鋁合金膜片密封。
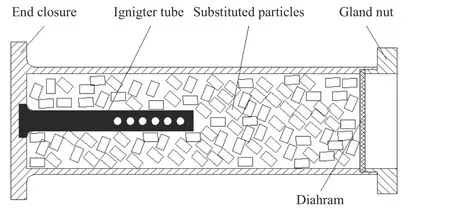
圖1 裝藥結(jié)構(gòu)示意圖Fig.1 Schematic of the charge structure
根據(jù)上述模型建立真實藥粒運(yùn)動燃燒和假藥粒運(yùn)動的兩相流模型,為了簡化內(nèi)彈道數(shù)值模擬的復(fù)雜性,需對實際物理過程進(jìn)行適當(dāng)假設(shè),基本假設(shè)如下:
(1)采用雙流體模型假設(shè),將發(fā)射藥顆粒群作為具有連續(xù)介質(zhì)特性的擬流體來處理;
(2)忽略湍流影響和氣固兩相間黏性;
(3)火藥顆粒服從幾何燃燒和指數(shù)燃燒定律[2];
(4)氣相狀態(tài)方程采用Nobel-Abel狀態(tài)方程[2];
(5)假設(shè)底火內(nèi)點(diǎn)火藥完全以燃?xì)庑问郊尤朦c(diǎn)火管內(nèi),點(diǎn)火管采用一維兩相流計算,破膜后源項在膛內(nèi)當(dāng)?shù)蒯尫牛?/p>
(6)假藥粒不產(chǎn)生燃?xì)猓叽缗c真實藥粒相同。
1.2 膛內(nèi)軸對稱二維兩相流方程組
對于內(nèi)彈道膛內(nèi)氣-固兩相流過程,由于膛內(nèi)沿身管軸線方向呈對稱形式,因此在內(nèi)彈道膛內(nèi)氣-固兩相流二維計算時,往往采用軸對稱模型,守恒形式可以表示如下:

式中:U為時間守恒矢量,F(xiàn)、G分別為徑向和軸向的矢通量,H為軸對稱變換矢量,S為源項。具體可表示如下:


提供輔助方程來封閉基本方程。膛內(nèi)點(diǎn)傳火過程源項由點(diǎn)火管提供,點(diǎn)火管為一維線源,從破膜后點(diǎn)火燃?xì)饬魅胩艃?nèi)過程視為源項當(dāng)?shù)蒯尫拧T错椗c膛內(nèi)燃燒過程進(jìn)行耦合計算,具體一維點(diǎn)火管控制方程及流出流量公式可參考文獻(xiàn)[5],其他如狀態(tài)方程、燃燒規(guī)律、相間阻力、相間傳熱、顆粒間應(yīng)力、顆粒表面溫度等輔助方程等參見文獻(xiàn)[2]。
2 數(shù)值計算方法
基于有限差分法,對上述模型在時間項上采用三階TVD型龍格庫塔法進(jìn)行時間推進(jìn),空間項采用五階WENO格式進(jìn)行空間離散。
2.1 五階WENO格式
WENO格式基本思路是將基架點(diǎn)分為多個組,每個組獨(dú)立計算某一點(diǎn)的導(dǎo)數(shù)逼近,得到多個差分,由于流場中間斷不可能處處存在,所以根據(jù)每個模板的光滑程度,設(shè)定權(quán)重,如果光滑度越高,則權(quán)重越大,存在間斷則權(quán)重趨近零。
對于向量形式的守恒方程:

采用全局Lax-Friedrichs分裂對空間項F、G進(jìn)行流通矢量分裂:
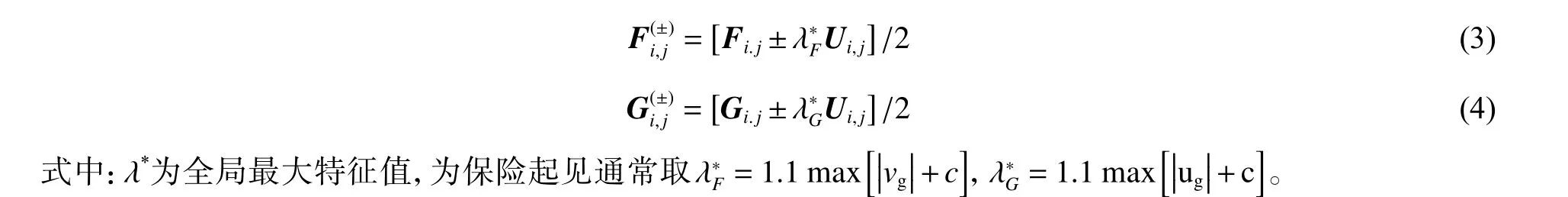
利用分裂后的矢通量構(gòu)造矢通量空間導(dǎo)數(shù)項的差分逼近式,以F項為例:

采用Jiang 等[14]的五階精度WENO格式構(gòu)造矢通量導(dǎo)數(shù)逼近式的通量形式為(以正特征值為例):

hj+1/2為正通量,由3個通量加權(quán)平均而得:

加權(quán)系數(shù)為(k=1,2,3):

式中:C1=1/10,C2=6/10,C3=3/10,ε0=10?6,β=2,Ik為光滑度量因子。Ik的表達(dá)式為:
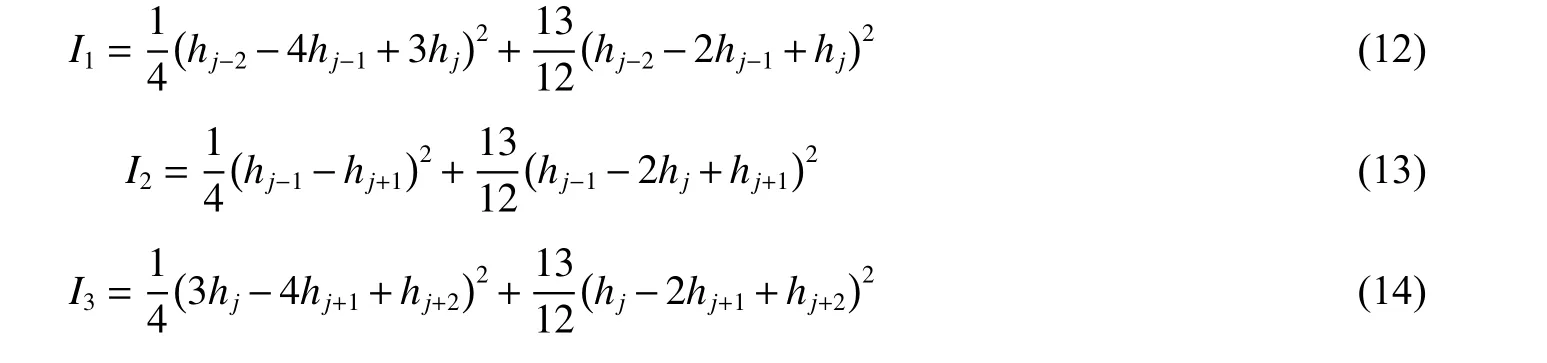
當(dāng)特征值為負(fù)時,利用對稱性,將上式中所有下標(biāo)“j+m”換成“j?m”即可。對G項的離散同理。
2.2 時間方向離散
空間導(dǎo)數(shù)離散化后的半離散方程為:

式中:Q n為離散后空間導(dǎo)數(shù)項,R n為源項。使用三階TVD龍格庫塔方法進(jìn)行離散:
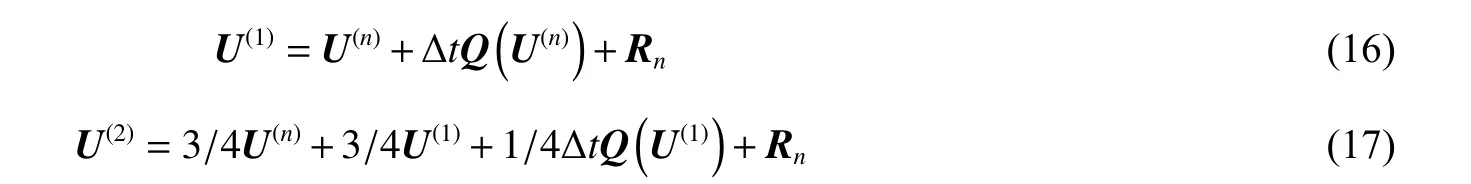
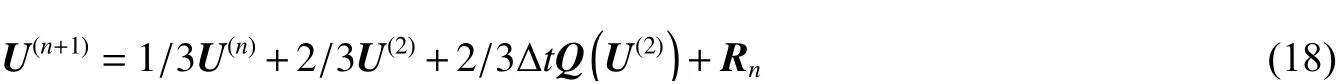
?t為時間步長,可以根據(jù)下式確定:

式中:C為柯朗數(shù),dx為計算網(wǎng)格尺度;λ*為全局最大特征值,由上述算法可計算得出。
2.3 初始條件和邊界條件
膛內(nèi)裝填條件采用如圖1所示的裝填結(jié)構(gòu),并結(jié)合實驗裝填數(shù)據(jù)和環(huán)境參數(shù),確定模擬過程中的初始條件。膛底和出口處邊界條件采用鏡面反射方法,計算至膜片破裂。由于WENO格式采用多個基架點(diǎn)進(jìn)行計算,在邊界外設(shè)置3個虛擬點(diǎn)可將邊界點(diǎn)轉(zhuǎn)化為內(nèi)點(diǎn)參與計算,還可以保持邊界點(diǎn)的計算精度。中心軸線邊界滿足軸對稱關(guān)系式。
3 實驗驗證與數(shù)值結(jié)果分析
3.1 假藥粒實驗
為了驗證所建立模型和數(shù)值方法的可靠性,對假藥粒情況進(jìn)行實驗驗證。采用了針對105 mm 口徑火炮藥室縮比的可視化實驗裝置,如圖2所示。裝置一端端蓋內(nèi)側(cè)連接點(diǎn)火管,外側(cè)可以裝底火,用以激發(fā)點(diǎn)火點(diǎn)燃點(diǎn)火管內(nèi)的點(diǎn)火藥;另一端端蓋為中通結(jié)構(gòu),用以鎖緊閉壓膜片。裝置中間裝有耐高壓玻璃管,管內(nèi)裝有定量的假藥粒,通過裝置中部預(yù)留的矩形窗口可以有效觀測裝置內(nèi)部的實驗現(xiàn)象。裝置上方設(shè)置3 個傳感器接頭,分別對應(yīng)藥室的膛底、中部和彈底(膜片)處,可以通過壓力傳感器測得這幾處的壓力。
整體實驗裝置如圖2所示,可視化窗口為400 mm×120 mm,高速攝像系統(tǒng)可通過此窗口拍攝實驗過程中火焰發(fā)展傳播過程。傳感器距膛底分別為40、247.5和455 mm,可通過數(shù)據(jù)采集系統(tǒng)獲取各位置壓力。整體實驗裝填點(diǎn)火藥為2#小粒黑火藥,質(zhì)量為30 g;假藥粒為PA 尼龍,質(zhì)量為3 kg;膜片為鋁合金,厚度為0.5 mm。

圖2 可視化實驗裝置Fig.2 Visual experimental system
3.2 數(shù)值計算與實驗數(shù)據(jù)比對
以上述實驗裝置進(jìn)行可視化模擬實驗的內(nèi)彈道過程二維兩相流動為研究對象,其具體結(jié)構(gòu)可參見圖1中的簡化物理模型,計算參量設(shè)置為:點(diǎn)火藥質(zhì)量,30.0 g;點(diǎn)火藥密度,1650 kg/m3;點(diǎn)火藥燃速指數(shù),0.98;點(diǎn)火藥燃速系數(shù),3.68 mm·s?1·MPa?0.98;火藥力,300 J/g;點(diǎn)火藥平均直徑,1 mm;假藥粒密度,1100 kg/m3;假藥粒質(zhì)量,3.0 kg;藥室長度,495 mm;藥室直徑,110 mm;點(diǎn)火管長度,25 mm;點(diǎn)火管直徑,19 mm;氣體絕熱指數(shù),1.3;網(wǎng)格長度,5 mm;氣體余容,1 cm3/g。
為了簡化計算,忽略點(diǎn)火管的二維效應(yīng),即在傳火孔破膜后將點(diǎn)火管作為線性點(diǎn)火源加入膛內(nèi)進(jìn)行兩相耦合計算,彈底與膛底為垂直于軸向的固壁平面,采用反射壁面條件。通過壓力傳感器對膛內(nèi)各位置采集的壓力與數(shù)值模擬獲取壓力進(jìn)行比對,由于模擬計算只到破膜后截止,因此只取破膜前的壓力進(jìn)行對比分析。
圖3所示為中間測點(diǎn)壓力隨時間變化的實驗結(jié)果與模擬結(jié)果的對比曲線。可以看出,模擬結(jié)果與實驗結(jié)果符合較好,全局平均誤差為5.35%,最高峰值處(即2.5 ms后區(qū)域)誤差僅為1.42%,說明所建立的模型和采用的數(shù)值方法合理有效。
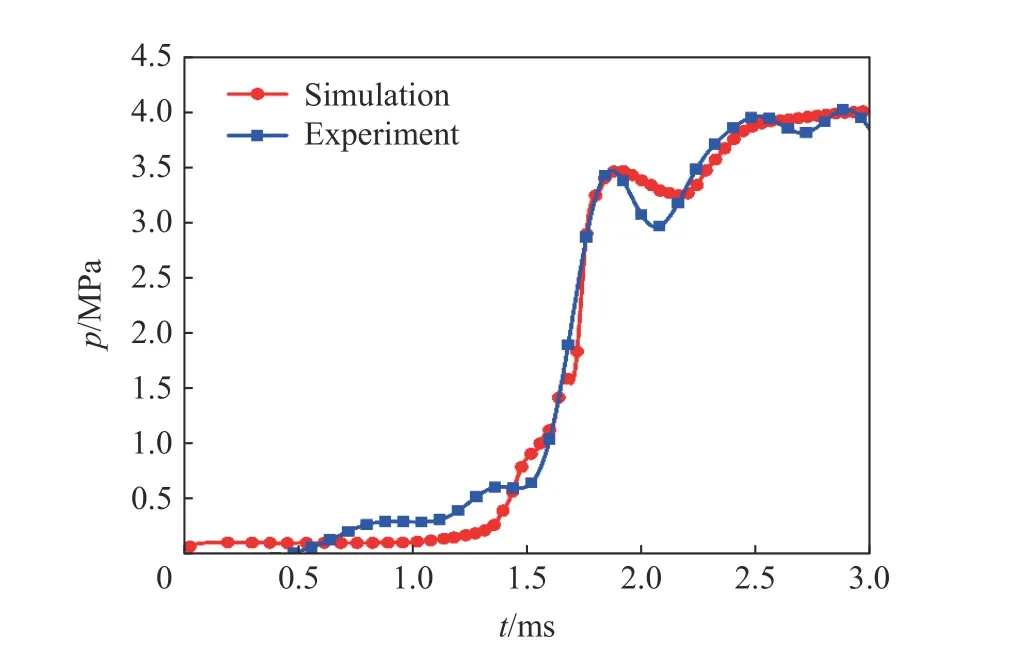
圖3 計算壓力曲線與實驗對比圖Fig.3 Comparison of pressure-time curves between numerical simulation and experiment
整個膛內(nèi)點(diǎn)傳火過程從點(diǎn)火管火藥點(diǎn)燃開始,高溫高壓燃?xì)饨?jīng)由點(diǎn)火管小孔流入膛內(nèi),點(diǎn)燃主裝藥。燃?xì)庠邳c(diǎn)火管燃燒破膜以及在膛內(nèi)流動需要一定的時間,而壓力傳感器測點(diǎn)在管壁處,所以初始階段壓力基本沒有變化,從點(diǎn)火開始到1 ms時間段內(nèi),均保持在一個大氣壓左右;在隨后的1~2 ms時間段內(nèi),壓力快速上升,這是由于假藥粒裝填幾乎占滿整個藥室,藥室透氣性很差,藥室自由空間很小,膛內(nèi)壓力上升也較快;壓力會在到達(dá)峰值時,會產(chǎn)生波動現(xiàn)象,這種波動現(xiàn)象主要由于假藥粒裝填密度過高,裝藥床透氣性差,且假藥粒不會燃燒導(dǎo)致燃?xì)饬鲃有宰儾睿植繅毫a(chǎn)生振蕩。
3.3 膛內(nèi)兩相流動過程分析
通過高速攝像拍攝可視化實驗裝置內(nèi)火藥燃?xì)饬鲃舆^程,與計算得到的壓力場進(jìn)行對比,可以清晰反映火藥燃?xì)庠谔艃?nèi)的發(fā)展?fàn)顩r。由于可視化裝置只能觀察到膛內(nèi)部分區(qū)域火焰?zhèn)鞑ミ^程,而火焰反映了高溫燃?xì)獾牧鲃舆^程,進(jìn)而反映膛內(nèi)的壓力場的變化過程,因此對計算得到的壓力云圖進(jìn)行相對應(yīng)位置截取對比,如圖4所示。
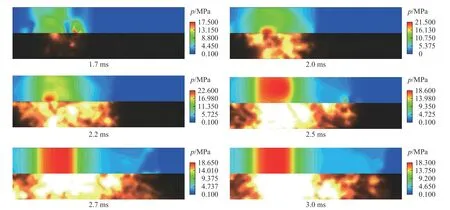
圖4 數(shù)值模擬壓力云圖與高速攝影圖像的對比Fig.4 Comparison between pressure clouds by numerical simulation and images by high-speed photography
整個點(diǎn)傳火可分為3 個階段;初始破孔階段,在壓力云圖中可以看出隨著點(diǎn)火管依次破孔,小孔破孔位置出現(xiàn)不同程度壓力梯度,而在高速攝影中,由于點(diǎn)火管被假藥粒包圍,很難直接觀測到初始階段的破孔現(xiàn)象;隨著點(diǎn)火管高溫燃?xì)獠粩嘞蛱艃?nèi)噴射,高溫燃?xì)庠谔艃?nèi)向膛壁和藥室兩端傳播,在壓力云圖中可以觀察到其壓力梯度沿徑向和軸向都有明顯的變化,相對應(yīng)的高速攝影圖像中,火焰?zhèn)鞑ヒ渤尸F(xiàn)與壓力云圖同樣的特征;到達(dá)2.5 ms時,點(diǎn)火管對應(yīng)的膛內(nèi)區(qū)域燃?xì)饬鲃釉趶较蛏匣疽恢拢囱貜较虻亩S效應(yīng)基本消失,而在遠(yuǎn)離點(diǎn)火管的區(qū)域仍存在一定的徑向效應(yīng),從點(diǎn)火管開孔處向膛底和彈底形成明顯的軸向壓力梯度。
為有效呈現(xiàn)膛內(nèi)壓力隨時間的發(fā)展變化,在徑向上取r=20 mm 處觀察壓力沿軸向的變化,如圖5所示。圖5(a)展示點(diǎn)火破膜初期階段(0.5~1.2 ms)膛內(nèi)壓力沿軸向的變化,這一階段膛內(nèi)徑向效應(yīng)明顯,壓力從破孔區(qū)域不斷上升,且隨著點(diǎn)火管依次破孔,壓力出現(xiàn)了相對應(yīng)的峰值,并逐漸向周圍發(fā)展。隨著點(diǎn)火管燃?xì)獠粩嘞蛱艃?nèi)噴射,點(diǎn)火管對應(yīng)的膛內(nèi)區(qū)域壓力基本趨于穩(wěn)定,如圖5(b)所示:2.5 ms后中心位置壓力約18 MPa,徑向壓力梯度基本消失,此時在軸向壓力梯度作用下,燃?xì)庀蛩幨覂啥藗鞑ィ诺缀蛷椀椎膲毫Σ粩嗌撸剌S向壓力變化區(qū)域也不斷增大。
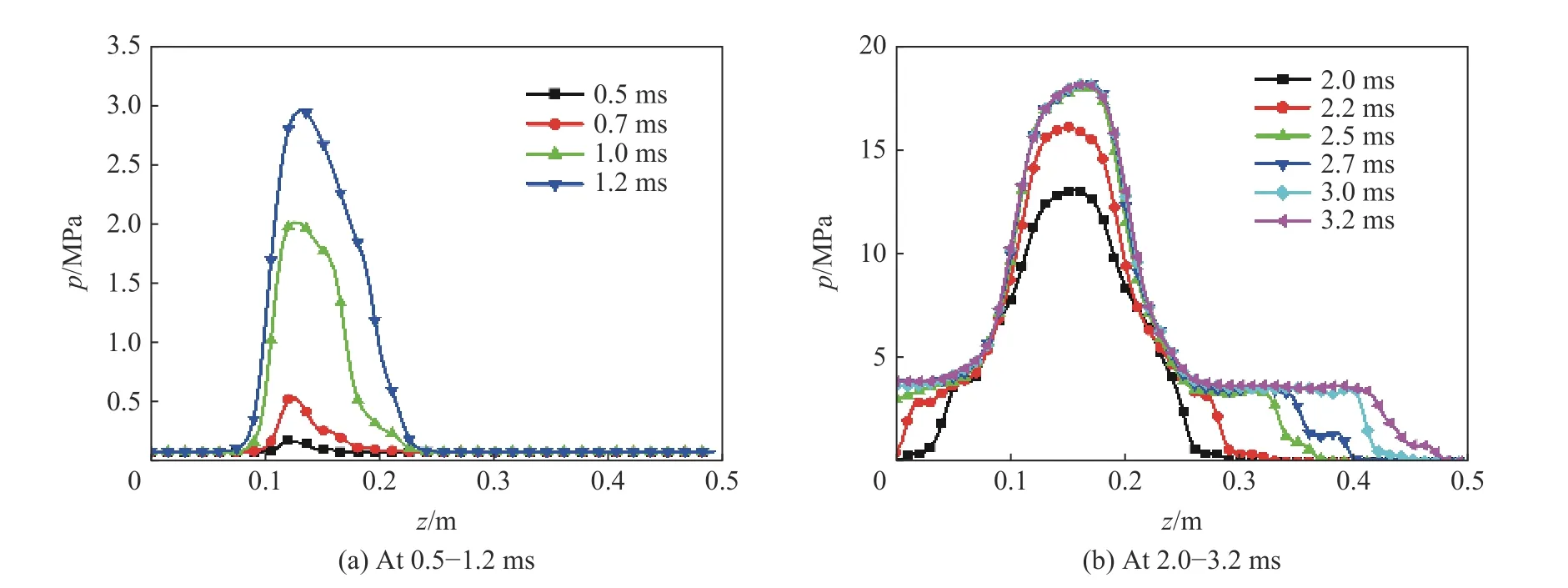
圖5 r=20 mm 處沿軸向方向的壓力分布Fig.5 Pressure distributions along the axis at r=20 mm
圖6和圖7描述了r=20 mm 處膛內(nèi)氣相的徑向速度和軸向速度沿藥室軸向的變化規(guī)律。從圖6可以看出,點(diǎn)火管破孔初始階段,燃?xì)獠粩鄰狞c(diǎn)火管內(nèi)流向膛內(nèi),此時點(diǎn)火管附近區(qū)域燃?xì)獾膹较蛩俣纫h(yuǎn)大于其軸向速度,沿徑向傳播也比較快。初始破孔階段,由于膛內(nèi)壓力遠(yuǎn)低于管內(nèi)壓力,氣體噴射出來速度極大(由于壓力差導(dǎo)致由點(diǎn)火管流入膛內(nèi)氣相速度很大),隨著燃?xì)獠粩嗔魅耄瑥较驂毫Σ钭冃。瑥较虻娜細(xì)馑俣纫仓饾u降低。
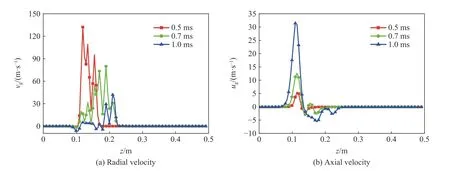
圖6 0.5~1.0 ms 不同時刻r=20 mm 處沿軸向方向的氣相速度分布Fig.6 Gas phase velocity distributions along theaxis at r=20 mm and different times from 0.5 msto 1.0 ms
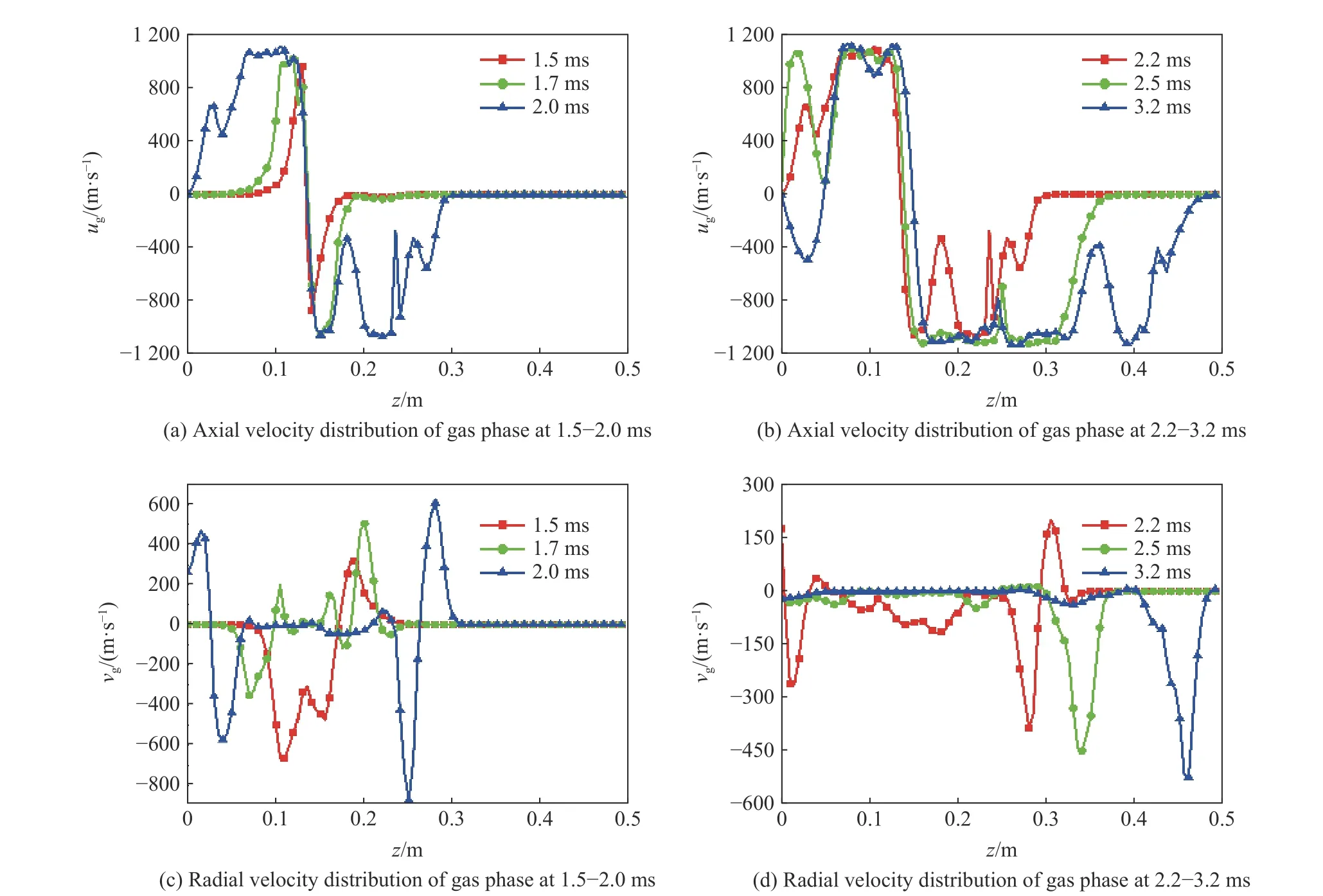
圖7 1.5~3.2 ms不同時刻r=20 mm 處氣相速度沿軸向的分布Fig.7 Gas phase velocity distributions along theaxis at r=20 mm and different times from 1.5 msto 3.2 ms
在點(diǎn)火1.5 ms后,大量燃?xì)庥牲c(diǎn)火管破孔處向兩端流動,并逐漸堆積形成高壓區(qū),在1.5~2.0 ms內(nèi),燃?xì)庵饾u向膛底和彈底運(yùn)動,氣相軸向速度漸漸升高,如圖7(a)所示;待燃?xì)膺\(yùn)動到膛底或彈底時遇到阻力后又氣相軸向速度慢慢降低至反向運(yùn)動,如圖7(b)所示,由于高密度裝填,在彈底形成了藥粒壅塞,所以氣相速度在接近彈底處已開始有反向的波動;隨著燃?xì)廨S向運(yùn)動加劇,燃?xì)獾膹较蛩俣仍邳c(diǎn)火管對應(yīng)區(qū)域基本為零,在2.0 ms前燃?xì)庀蛱诺缀蛷椀追较騻鞑ィ捎谌細(xì)鈮毫^低,初始傳播時受顆粒擾動較大,徑向速度波動劇烈,如圖7(c)所示;2.2 ms后,由于燃?xì)獬溆诺缀椭胁繀^(qū)域,燃?xì)鈴较蛩俣瘸谔诺子行》秶▌油猓渌麉^(qū)域燃?xì)鈴较蛩俣冉禐榱悖細(xì)獾膹较驍_動逐漸向彈底傳播,如圖7(d)所示。
火藥顆粒運(yùn)動對初始階段膛內(nèi)點(diǎn)傳火研究很重要,為進(jìn)一步研究藥床中藥粒運(yùn)動規(guī)律,圖8~9展示了r=20 mm 膛內(nèi)固相速度沿藥室軸向發(fā)展變化。從圖8可以看出,破孔初始階段火藥顆粒軸向和徑向速度非常低,最高速度不超過0.5 m/s,說明膛內(nèi)的火藥顆粒基本保持不動,呈現(xiàn)一種多孔介質(zhì)狀態(tài)。從實驗實際拍攝的高速影像來看,固相顆粒確實未發(fā)生大范圍運(yùn)動。
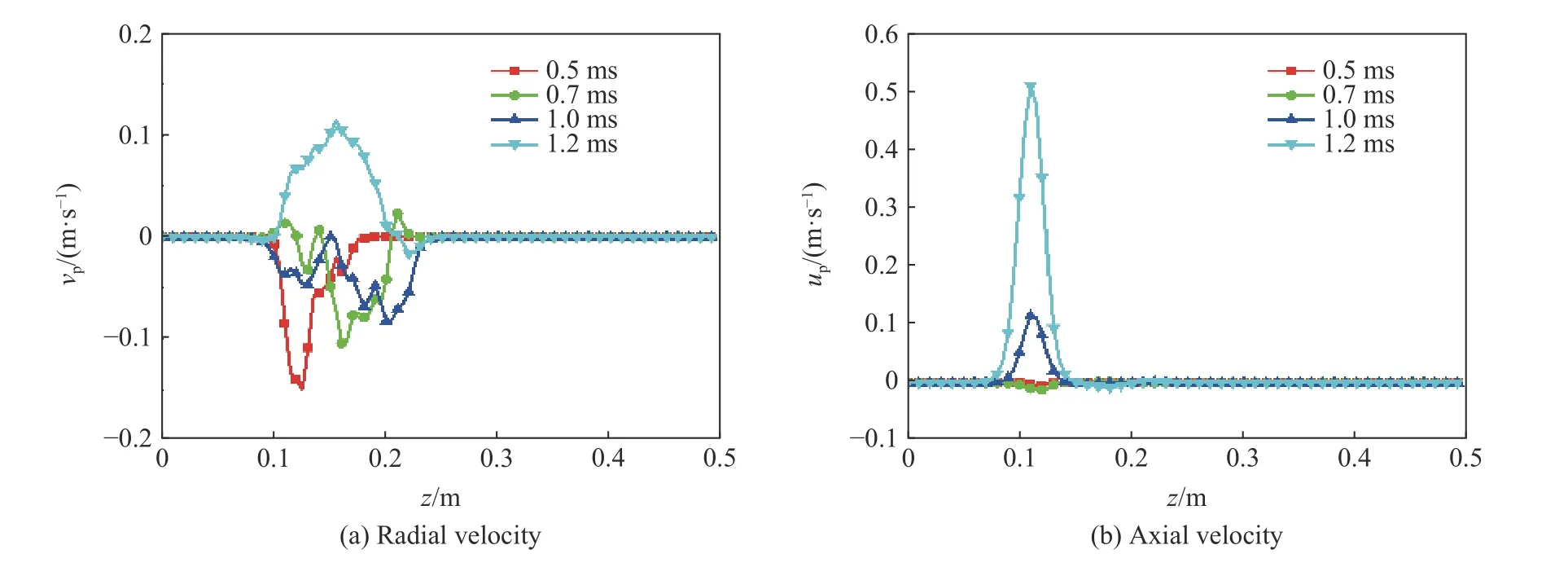
圖8 0.5~1.2 ms不同時刻r=20 mm 處固相速度沿軸向的分布Fig.8 Solid phase velocity distributionsalong the axis at r=20 mm and different times from 0.5 ms to 1.2 ms
隨著火藥燃?xì)庠谒幋矁?nèi)不斷流動,勢必會帶動火藥顆粒運(yùn)動。在高密度裝填的藥床中,火藥顆粒可運(yùn)動的范圍十分有限,且模擬和實驗采用的假藥粒不會燃燒且變形較小,所以顆粒間相互作用力十分大,導(dǎo)致藥床內(nèi)的固相速度非常低。如圖9(a)所示,火藥顆粒徑向速度隨時間發(fā)展逐漸為零,從破孔位置沿軸向至彈底方向有一定的徑向速度,至膛底處徑向速度也逐漸趨向于零,與徑向氣相速度相對應(yīng),說明氣相速度也是影響顆粒運(yùn)動的重要原因。圖9(b)中火藥顆粒軸向速度也驗證了這一點(diǎn),由于燃?xì)廨S向壓力梯度大,氣相軸向速度高,所以導(dǎo)致火藥顆粒向膛底和彈底兩側(cè)運(yùn)動速度較高。在真實裝藥情況下,會造成膛底火藥粒擠壓破碎,形成小范圍高壓區(qū)域,繼而推動藥床向彈底運(yùn)動。
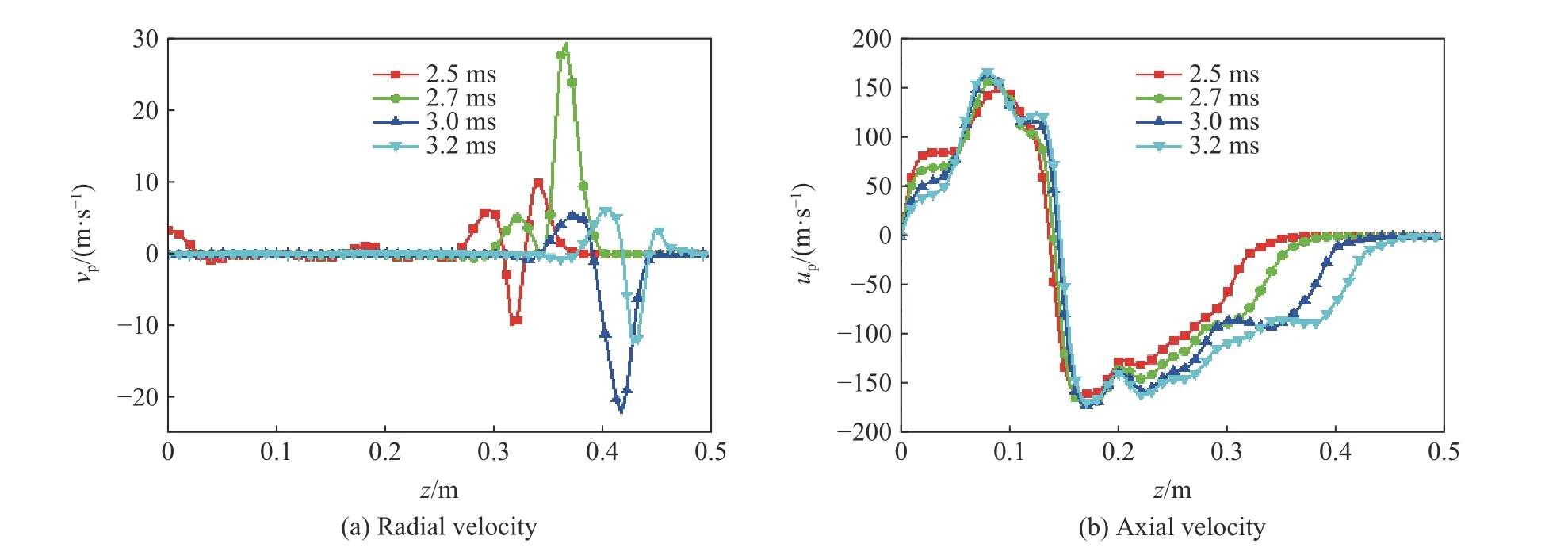
圖9 2.5~3.2 ms不同時刻r=20 mm 處固相速度沿軸向的分布Fig.9 Solid phase velocity distributionsalong the axis at r=20 mm and different times from 2.5 ms to 3.2 ms
4 結(jié) 論
以火炮膛內(nèi)初期點(diǎn)傳火性能研究為背景,建立了軸對稱二維兩相流數(shù)理模型,對假藥粒進(jìn)行相應(yīng)合理化假設(shè),在空間上采用五階WENO格式進(jìn)行空間離散,時間上采用三階TVD型龍格庫塔法進(jìn)行時間推進(jìn),并進(jìn)行實驗與數(shù)值模擬對比研究。數(shù)值分析了點(diǎn)火初期膛內(nèi)壓力的發(fā)展及氣固兩相速度,具體結(jié)論如下。
(1)可視化實驗裝置與高精度數(shù)值方法,有效模擬了初始階段點(diǎn)火燃?xì)庠谒幋仓械膫鞑ヒ?guī)律,通過與可視化實驗平臺測試數(shù)據(jù)和現(xiàn)象進(jìn)行對比,驗證了數(shù)理模型和數(shù)值方法的有效性。
(2)點(diǎn)火初期膛內(nèi)徑向效應(yīng)明顯,隨著傳火不斷進(jìn)行,點(diǎn)火管對應(yīng)膛內(nèi)區(qū)域徑向效應(yīng)逐漸消失,燃?xì)獾妮S向傳播開始占據(jù)主導(dǎo)地位,膛內(nèi)壓力呈現(xiàn)徑向一致、軸向梯度分布的特征。
(3)通過數(shù)值模擬與實驗觀測可以得出,在高密度裝填情況下,初始階段藥床藥粒基本不會發(fā)生運(yùn)動,最高速度為0.5 m/s,后續(xù)固相速度的發(fā)展與氣相速度有緊密的關(guān)系;氣相速度在初始階段沿徑向傳播較快,后續(xù)在軸向壓力梯度作用下,軸向速度開始占據(jù)主導(dǎo),在膛底和中部區(qū)域氣相速度降低為零,徑向速度擾動也逐漸向彈底傳播,在到達(dá)彈底之前由于藥粒壅塞現(xiàn)象導(dǎo)致阻力變大,氣相速度會出現(xiàn)振蕩。

