爆炸載荷特征參數對無限長圓柱殼彈性動態響應的影響*

張鵬宙，董 奇，楊 沙

（中國工程物理研究院化工材料研究所，四川 綿陽 621999）

爆炸容器作為一種具有特殊用途的密封壓力容器，主要用來約束一定量的炸藥等易爆物質在其內部爆炸后產生的效應[1]。這種形式的爆炸屬于密閉空間爆炸，而密閉空間或半密閉空間的爆炸統稱為有限空間爆炸[2]。爆炸容器按結構外形可分為球形和圓柱形爆炸容器，柱殼相比于球殼更易加工生產，因此柱殼的應用更廣泛。

對爆炸或沖擊載荷作用下爆炸容器的殼體響應，已進行了大量的研究。Baker[3]首先利用單自由度（single degree of freedom，SDOF）模型研究了內部中心受到三角脈沖載荷作用的薄壁球殼，對其徑向位移進行了理論求解，得到了彈性動態響應的位移解析解，還獲得了采用雙線性等向強化材料的球殼在小應變條件下彈塑性動態響應的位移解析解。接著，有了很多SDOF模型應用：Ko等[4]利用SDOF 模型對多層彈塑性球殼受到內部軸對稱脈沖爆炸載荷作用下的響應進行了研究；趙士達[1]在SDOF 模型基礎上提出了動力系數法；Li等[5]、Dong 等[6]研究了采用彈塑性線性隨動強化材料的球殼及平面應力、平面應變圓環，利用SDOF模型及能量方法對結構受到內部中心軸對稱脈沖載荷作用后的動態響應進行了力學推導和數值模擬，發現了反直觀現象的存在及其出現的臨界條件。還有對爆炸載荷下首個脈沖載荷對結構影響的研究[3,7-8]。

孫琦等[9-11]在文獻[12-14]基礎上，考慮爆炸載荷準靜態階段的影響將爆炸載荷簡化為含有三角脈沖階段及后續準靜壓階段的載荷，利用SDOF 模型研究了內部簡化爆炸載荷作用下球殼的彈性及彈塑性動態響應過程：提出了球殼的徑向位移解析解及其最大值；發現了影響位移最大值所處載荷階段的臨界時刻；分析了準靜態壓力對動態響應過程中最大位移及后期準靜壓階段振幅的影響。并且當載荷分界點時刻晚于臨界時刻時，獲得了通過臨界準靜壓用以判斷徑向位移最大值出現時刻的區域圖。然而，該圖僅適用于三角脈沖沖量恒定、且結構的幾何、材料參數等均為特定值的情況，存在很大局限性。

關于球殼徑向位移響應的解析求解[9-10]、平面應力、平面應變圓環的相關研究[5-6,15]均屬于一維問題，有限長圓柱殼在兩端面滑動-滑動邊界條件下的響應[16]與軸向位置無關也屬于一維問題。但有限長圓柱殼在兩端面自由-自由、簡支-簡支邊界條件下的響應[16]與軸向位置有關屬于二維問題。考慮柱殼理論求解的可行性，本文中研究柱殼響應的一維問題，研究的對象為內部中心受到沿其軸向線性裝藥的無限長圓柱殼，屬于平面應變問題。本文模型可等效為平面應變圓環[15]，或可等效為處于兩光滑剛性墻體間的有限長圓柱殼即兩端面受到軸向位移約束的有限長圓柱殼[16]，不考慮結構缺陷、屈曲和拉伸頸縮。

與文獻[10]不同，本文中對無限長圓柱殼結構在內爆炸載荷作用下的動態響應進行研究。從準靜壓與三角脈沖峰值比和三角脈沖作用時間入手，并結合結構的呼吸頻率，通過兩個無量綱量獲得徑向位移最大值所處載荷階段的分區圖，適用性更廣泛。從已開展的研究來看，三角脈沖載荷以及準靜壓載荷對結構動態響應的影響均較大，然而綜合考慮這兩者對結構動態響應影響的相關研究較少，本文中綜合考慮載荷的三角脈沖載荷以及準靜壓載荷的影響，獲得載荷參數及無量綱參數對結構彈性動態響應的影響規律，有助于深入認識爆炸載荷下圓柱殼的動態響應規律。本文的研究思路對于球殼的一維響應問題也有一定參考價值。

1 徑向位移理論求解

考慮爆炸載荷準靜壓階段對無限長圓柱殼動態響應的影響，采用球殼相關研究[9-11]中應用的爆炸載荷模型。圖1（a）為簡化爆炸載荷p(t)，含有三角脈沖階段及后續準靜壓階段：

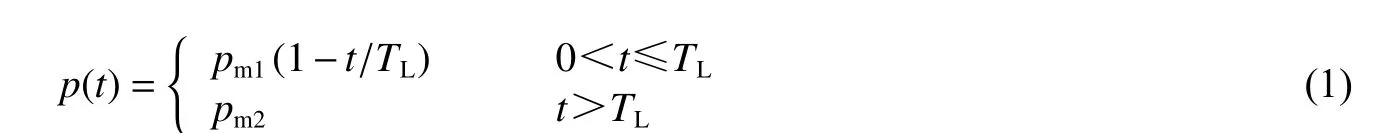
式中：pm1為三角脈沖峰值，TL為載荷分界點時刻即三角脈沖作用時間，pm2為準靜壓，取λ=pm2/pm1，0≤λ＜1。考慮有限元建模因素，無限長圓柱殼也可等效為平面應變圓環，圖1（b）為內部受到均勻分布式簡化爆炸載荷的無限長圓柱殼橫切面。無限長圓柱殼的幾何尺寸為：中線半徑r=41 mm，徑向厚度h=2 mm；材料參數為：密度ρ=7 830 kg/m3，彈性模量E=200 GPa，泊松比μ=0.3。徑向位移為ur，周向應力為σθ。

對于內部中心爆炸載荷作用下的無限長圓柱殼，SDOF運動方程為[5,15]：

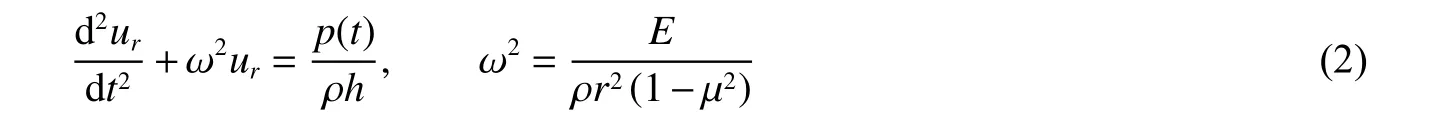
式中：ω為呼吸振動頻率，振動周期為T=2π/ω。

假定在彈性運動階段結構變形小，因此無限長圓柱殼的中線半徑變化微小，可認為振動頻率ω近似為常量。由式（1）～（2），可得無限長圓柱殼徑向位移響應的解析解：

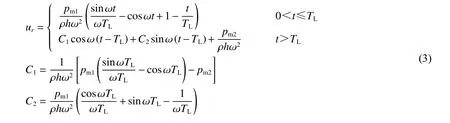
式（3）在形式上與爆炸載荷下球殼彈性階段的位移解[9]相同，但在球殼研究中ω2=2E/[ρr2(1?μ)]。

2 徑向位移最大值響應分析

反映無限長圓柱殼結構幾何及材料特性的有獨立參數h、r、ρ、E、μ及相關參數ω，反映載荷特征的有獨立參數TL、pm1、pm2及相關參數λ，這些均屬于動力響應影響因素。本節中將針對徑向位移最大值ur,max綜合研究ω、TL、pm1、pm2及λ 等關鍵因素的影響規律。

2.1 徑向位移最大值所處載荷階段的判別

無限長圓柱殼與球殼同為對稱結構，有相似之處。在球殼的相關研究中，孫琦等[9-10]通過式（4）～（7）給出了球殼的臨界時刻tc及徑向位移最大值。這些同樣適用于無限長圓柱殼，但兩者的呼吸振動頻率ω 不同。對于本文結構，tc=18.0μs、TL=tc時徑向位移最大值恰好出現在載荷分界點處，即三角脈沖與準靜壓階段的交界處，在徑向位移曲線上第一個波峰剛好出現在載荷分界點處：

無限長圓柱殼的徑向位移響應也需根據TL與tc的關系，分三種情況。

（1）當TL＜tc即ωTL＜7/3時，徑向位移最大值首次出現時刻處于準靜壓階段，此時準靜壓階段徑向位移最大值為：

（2）當TL=tc即ωTL=7/3時，徑向位移最大值首次出現時刻處于載荷分界點處，分界點處徑向位移最大值為：

（3）當TL＞tc即ωTL＞7/3時，徑向位移響應曲線在三角脈沖和準靜壓階段均有波峰出現，三角脈沖階段的徑向位移最大值為：

因而，徑向位移最大值為ur,max-qs和ur,max-tri兩者中的大者。由此，孫琦等[9-10]提出了臨界準靜壓pm2,c，當滿足TL＞tc、pm2=pm2,c時ur,max-qs=ur,max-tri。圖2為首個脈沖沖量恒定、不同pm1時的臨界準靜壓曲線[10]，可以通過pm2,c判斷TL＞tc時徑向位移最大值首次出現時刻所處的載荷階段：曲線上方區域Ⅰ，徑向位移最大值出現于準靜壓階段；曲線下方區域Ⅱ，徑向位移最大值出現于三角脈沖階段；區域Ⅲ內pm2＞pm1，不符合實際情況，不予考慮。圖2 適用于結構幾何參數r及材料參數ρ、E、v特定且首個脈沖沖量恒定的情況。

圖2 準靜態壓力臨界值[10]Fig. 2 Critical value of quasi-static pressure[10]

在無限長圓柱殼的研究中，當ωTL＞7/3時，如三角脈沖階段與準靜壓階段徑向位移最大值恰好相等，由式（5）、（7）可得到：

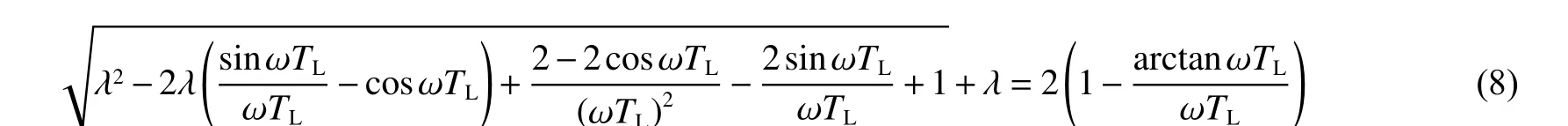
式（8）以ωTL為自變量、λ=pm2/pm1為因變量。圖3（a）為ωTL∈[7/3,25]時的λ-ωTL曲線：曲線上方區域ur,max-qs＞ur,max-tri，即準靜壓階段徑向位移最大；曲線下方區域ur,max-qs＜ur,max-tri，即三角脈沖階段徑向位移最大。不同類型炸藥λ∈[0,1]，如TNT炸藥λ≈0.1。對圖3（a）曲線上、下方的有效區域進行分區，獲得便于直觀判斷徑向位移達到最大值時所處載荷階段的分區圖，用來判斷當ωTL＞7/3時徑向位移最大值首次出現時刻所處載荷階段，如圖3（b）所示。如點（ωTL,λ）處于圖3（a）曲線上方，即圖3（b）中綠色區域，則徑向位移最大值出現在準靜壓階段；如點（ωTL,λ）處于圖3（a）曲線下方，即圖3（b）中黃色區域，則徑向位移最大值出現在三角脈沖階段；如點（ωTL,λ）在圖3（a）曲線上，則三角脈沖階段的徑向位移最大值與準靜壓階段的相等。圖3（b）適用于載荷參數和圓柱殼的幾何、材料參數為任意值的情況，在后續動力響應分析中起到主要指導作用。

圖3 當ωT L＞7/3時徑向位移達到最大值時所處載荷階段的分區Fig.3 Zoning diagram of theload stage when theradial displacement reaches the maximum value at ωT L＞7/3

2.2 徑向位移最大值響應規律

確定徑向位移最大值所處載荷階段后，討論ur,max的影響因素及其具體影響規律。本文中所用力學分析模型均已經過數值模擬校驗。

如ur,max出現在三角脈沖載荷階段，即ur,max=ur,max-tri，則ωTL∈(7/3,∞)。由式（7）可知，ur,max-tri與pm1成正比，與pm2無關。圖4（a）為TL=50μs、pm2=10 MPa、pm1分別為50、75、100 MPa 時的徑向位移曲線，對應的（ωTL,λ）分別為（6.461,0.2）、（6.461,0.133）、（6.461,0.1），這些點均處于圖3（b）的黃色區域，所以徑向位移最大值出現在三角脈沖載荷階段。徑向位移曲線的第一個波峰處于三角脈沖階段，且該峰值為徑向位移最大值，與pm1成正比。隨著TL的增大，徑向位移最大值ur,max-tri也增大。圖4（b）為pm1=100 MPa、pm2=10 MPa、TL分別為30、40、50μs時的徑向位移曲線，對應的（ωTL,λ）分別為（3.876 6,0.1）、（5.168 8,0.1）、（6.461,0.1），這些點均處于圖3（b）的黃色區域，所以徑向位移最大值出現在三角脈沖載荷階段。徑向位移曲線僅有第一個波峰處于三角脈沖階段，且該峰值為徑向位移最大值，隨著TL的增大而增大，原因是三角脈沖階段作用時間的增長導致相同時間段內圓環受到更大的沖量。

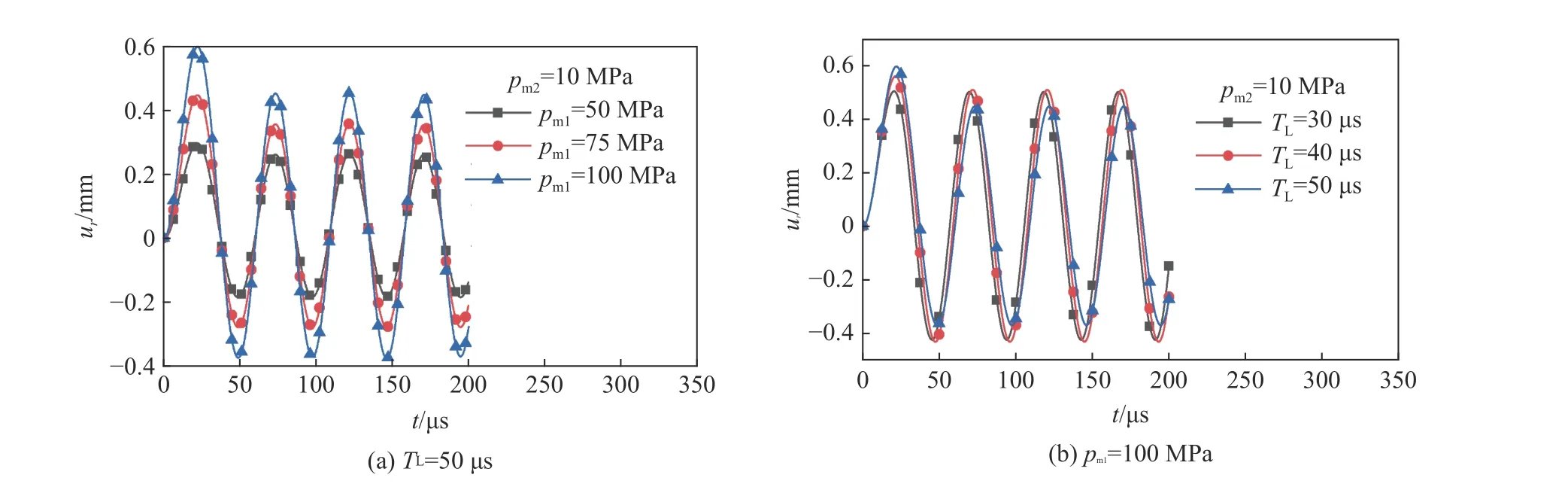
圖4 徑向位移曲線Fig.4 Radial displacement curves

如ur,max出現在載荷分界點處，即ur,max=ur,max-c，此時徑向位移最大值ur,max=pm1/(ρhω2)，ur,max與pm1成正比，且與pm2無關。圖5為TL=18μs、pm2=10 MPa、pm1分別為50、100、150 MPa 即ωTL=7/3時的徑向位移曲線，三角脈沖階段徑向位移最大值與準靜壓階段徑向位移最大值相等。徑向位移曲線的第一個波峰處于載荷分界點處，且該峰值為徑向位移最大值，與pm1成正比。

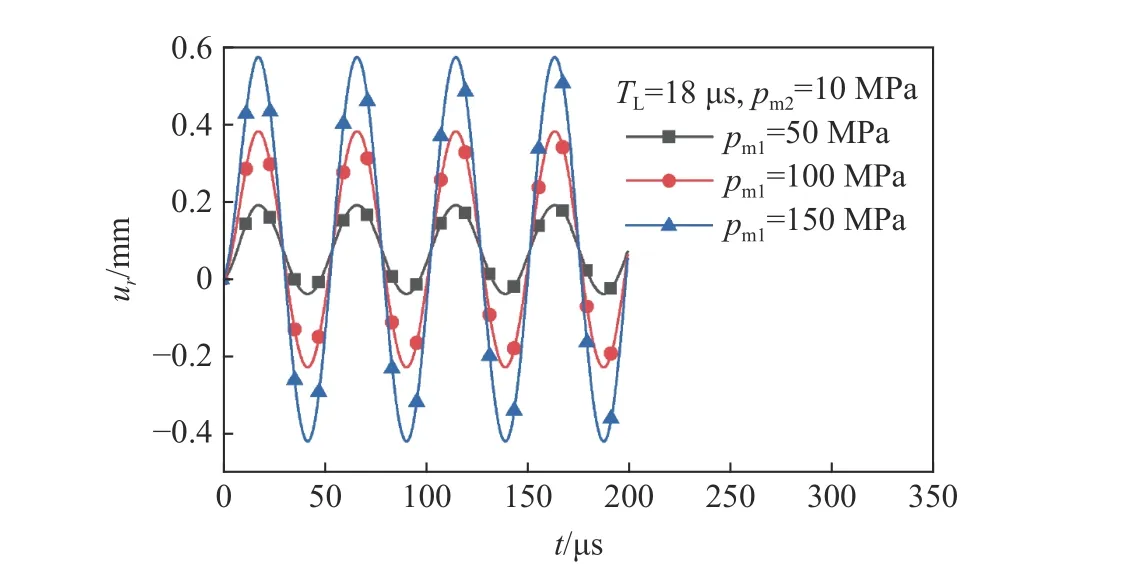
圖5 徑向位移曲線Fig.5 Radial displacement curves

如ur,max出現在準靜壓階段，即ur,max=ur,max-qs，由式（5）進行變換得到：

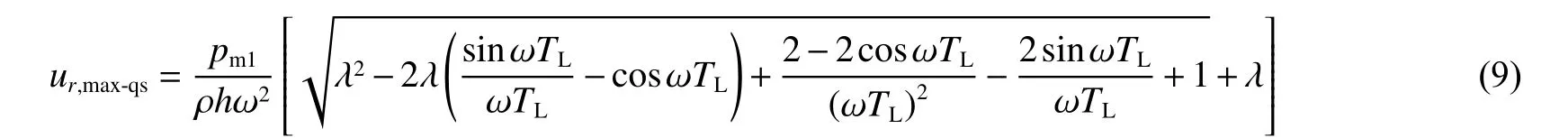
由式（9）可以看出：λ 為定值時徑向位移最大值與pm1成正比；當pm1為常數時，dur,max-qs/dλ＞0，隨著λ 的增大，準靜壓階段的徑向位移最大值也增大。圖6為λ=0.2、TL＜tc和TL＞tc時徑向位移最大值出現在準靜壓階段時的徑向位移曲線。圖6（a）中，ωTL=0.6461＜7/3，因此徑向位移最大值出現在準靜壓階段。圖6（b）中，對應的（ωTL,λ）均為（3.876 6,0.2），處于圖3（b）曲線的綠色區域，因此徑向位移最大值出現在準靜壓階段。圖6（a）中位移曲線的所有波峰均出現在準靜壓階段，圖6（b）中位移曲線第二個及其后的波峰均出現在準靜壓階段，由于準靜壓階段響應為彈性等幅振動，因此該階段峰值均為徑向位移最大值。

圖6 徑向位移曲線Fig.6 Radial displacement curves

3 準靜壓階段振幅分析

準靜壓階段的響應為彈性等幅振動，其振幅A為：

與球殼的解[9-10]形式一致，但球殼研究中通過枚舉法討論準靜壓對A的影響。因而，本文中從解析解入手，分析三角脈沖峰值pm1及準靜壓pm2對準靜壓階段彈性等幅振動的振幅A的影響規律。

3.1 p m1對振幅的影響規律

如僅考慮三角脈沖峰值pm1對振幅A的影響，將式（10）展開可得：

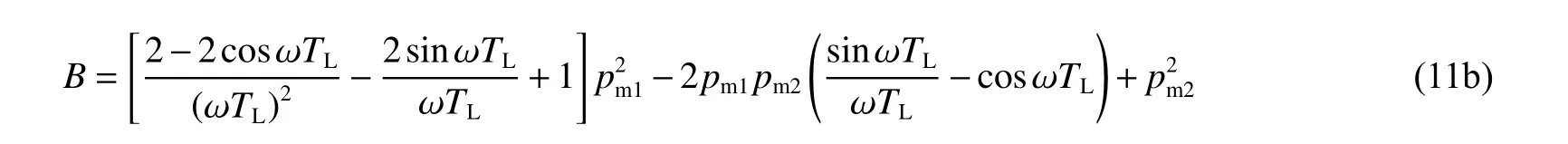
式（11b）是以pm1為自變量的二次函數，其二次項系數非負，當且僅當ωTL=0時等號成立：

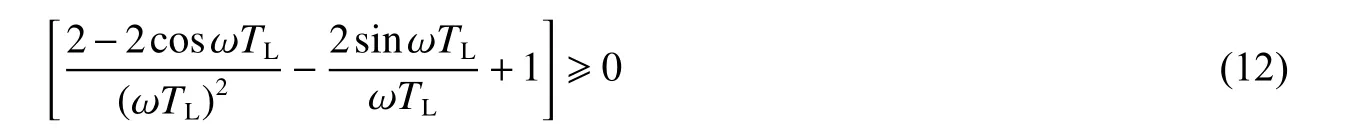
因此拋物線開口向上。式（11b）的對稱軸表達式，同樣也適用于式（11a）：

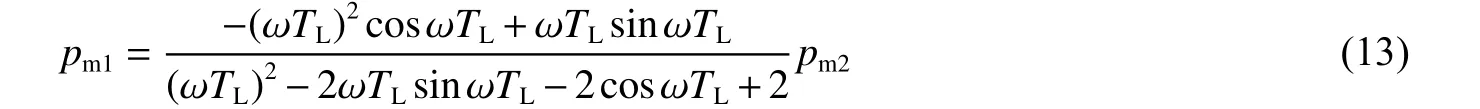
考慮pm1引起的λ 變化，即pm2為常數。圖7（a）為以ωTL為橫坐標、1/λ 為縱坐標時式（13）的曲線圖，其中曲線下方為振幅A關于1/λ 的單調遞減區域，曲線上方為單調遞增區域；圖7（b）對圖7（a）中的有效區域進行了分區，其中紅色區域內振幅A隨著λ 的增大而增大，綠色區域內振幅A隨著λ 的增大而減小。

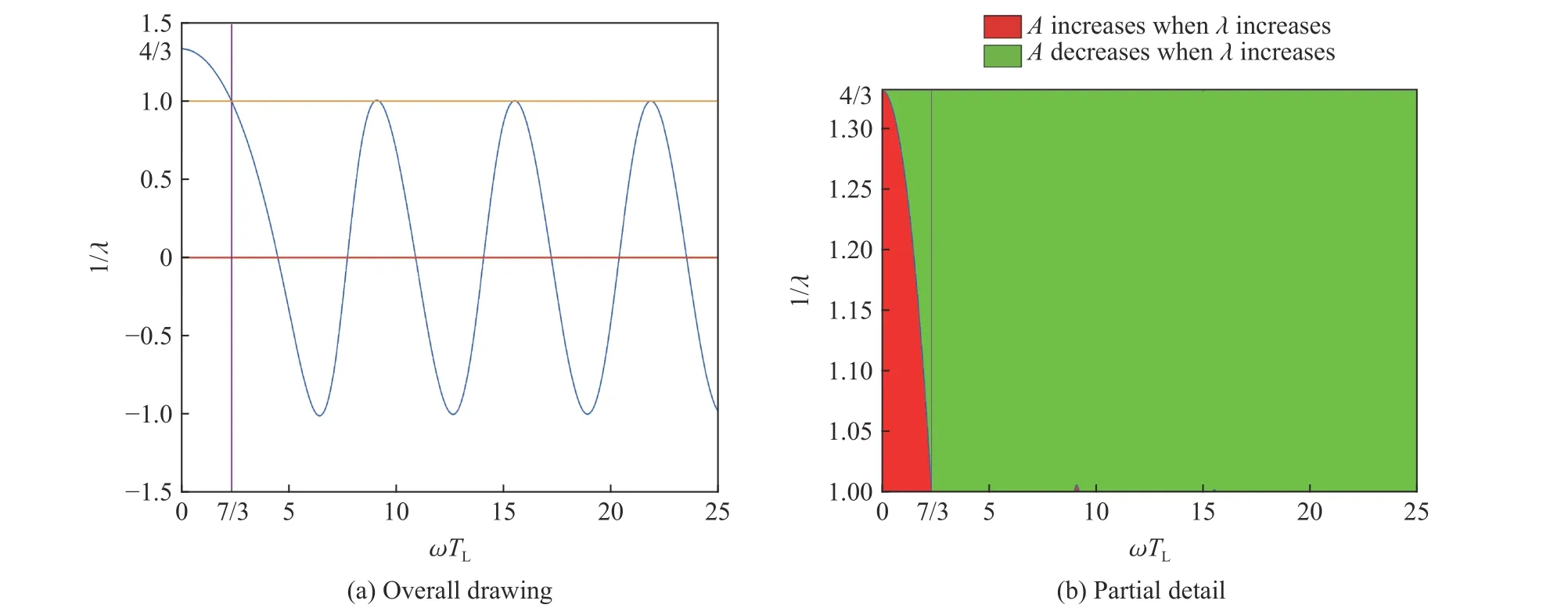
圖7 由p m1導致的準靜壓階段振幅單調性分區Fig.7 Monotonic zoning diagram of amplitude in quasi-static pressure stage caused by p m1

為了確定具體工況下pm1對準靜壓階段振幅的影響規律，先需要確定分區圖7（b）曲線上的坐標，選取TL=5μs時舉例說明，此時ωTL=0.646 1，在圖7（b）對應為(ωTL,1/λ)=(0.646 1,1.309)，則λ=0.763 9。圖8（a）為pm2=20 MPa、TL=5μs時振幅A隨λ 的變化曲線：振幅隨著[0,0.763 9]內λ 的增大而減小（見圖7（b）中綠色區域），隨著[0.763 9,1]內λ 的增大而增大（見圖7（b）中紅色區域）。圖8（b）為[0.5,1]區間的振幅變化曲線，可明顯看出λ=0.763 9附近的振幅變化過程。

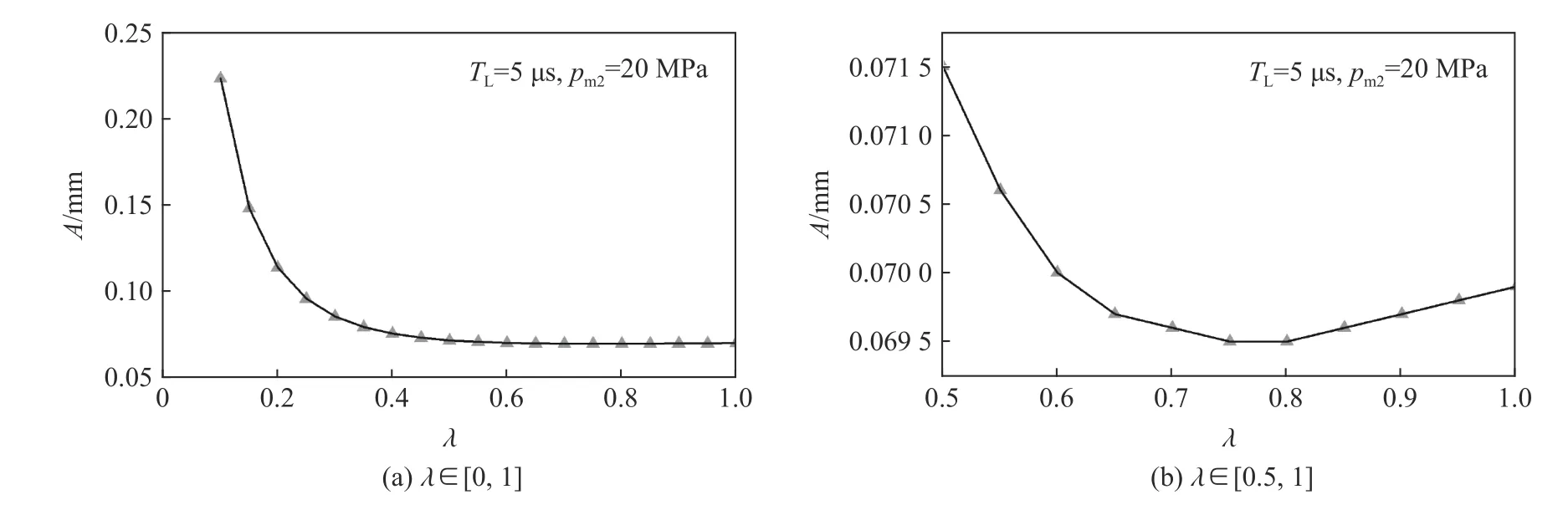
圖8 當λ 不同時準靜壓階段的振幅變化曲線Fig.8 Amplitude variation curves of quasi-static pressure stage with different λ

3.2 p m2 對振幅的影響規律

如僅考慮準靜壓pm2對A的影響，由式（11a）、（11b）可得：

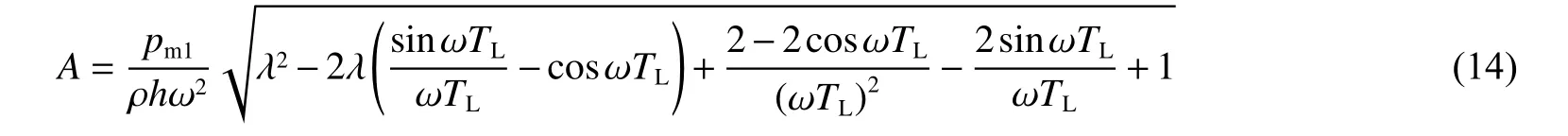
考慮pm2引起的λ 變化，即pm1為常數。如以λ 為自變量，式（14）的對稱軸表達式為：

圖9（a）為式（15）的曲線圖，圖9（b）為其有效區域的分區。其中，藍色區域內，振幅A隨著λ 的增大而減小；紅色區域內，振幅A隨著λ 的增大而增大；而黃綠相間區域內，振幅A隨著λ 的增大會先減小（黃色區域）后增大（綠色區域）。

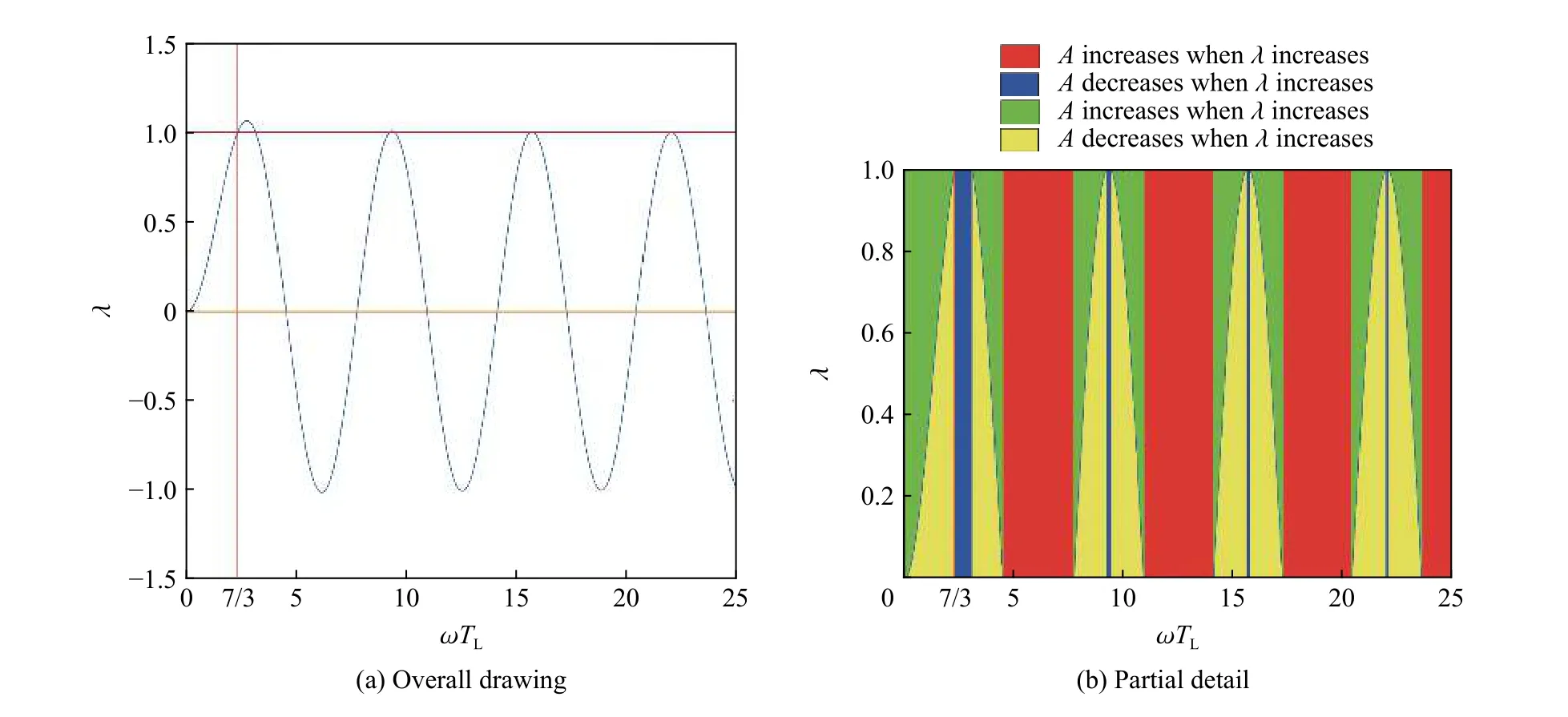
圖9 由p m2 導致的準靜壓階段振幅的單調性分區Fig.9 Monotonic zoning diagram of amplitudein quasi-static pressurestage caused by p m2

當ωTL＜7/3時，選取TL=10μs，則ωTL=1.292 2，在圖9（a）曲線上確定坐標(ωTL,λ)=(1.292 2,0.469 0)，則振幅A隨著(0,0.469 0)內λ 的增大而減小（見圖9（b）中黃色區域），隨著(0.469 0,1)內λ 的增大而增大（見圖9（b）綠色區域）。圖10為TL=10μs下由pm2引起λ 變化導致的準靜壓階段振幅變化曲線。

當ωTL=7/3時，則TL=18μs，在圖9（a）曲線上確定坐標(ωTL,λ)=(7/3,1)，振幅A隨著λ 的增大而減小（見圖9（b）中藍色區域）。圖10為TL=18μs下由pm2引起λ 變化導致的準靜壓階段振幅變化曲線。

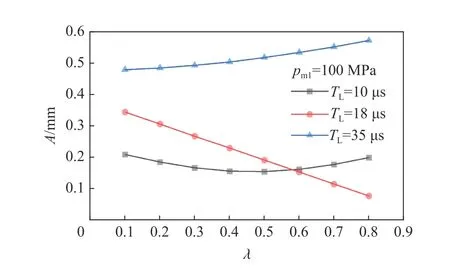
圖10 當λ 不同時準靜壓階段的振幅變化曲線Fig.10 Amplitude variation curves of quasi-static pressure stage with different λ

當ωTL＞7/3時，選取TL=35μs，則ωTL=4.522 7，在圖9（a）曲線上確定坐標(ωTL,λ)=(4.522 7,?0.028 6)，振幅A隨著λ 的增大而增大（見圖9（b）中紅色區域）。圖10為TL=35μs下由pm2引起λ 變化導致的準靜壓階段振幅變化曲線。

4 結 論

綜合考慮了載荷的三角脈沖階段以及準靜壓階段對無限長圓柱殼結構彈性動態響應的作用效果，從準靜壓與三角脈沖峰值比λ 入手，并結合結構的振動頻率ω 和三角脈沖作用時間TL，獲得了關鍵參數對結構彈性動態響應的影響規律。通過力學分析獲得可以直觀判斷徑向位移最大值出現時刻所處載荷階段的分區，還得到三角脈沖峰值和準靜壓峰值引起的準靜壓階段振幅單調性變化分區。

（1）當ωTL＜7/3時，徑向位移最大值ur,max出現在準靜壓階段；當ωTL=7/3時，ur,max剛好出現在載荷的分界點處；當ωTL＞7/3時，存在兩個無量綱量ωTL、λ，對ur,max所處載荷階段產生決定性作用，受自身振動頻率及載荷參數共同影響。

（2）若徑向位移最大值ur,max出現在三角脈沖階段，則ur,max與三角脈沖峰值成正比，且隨著三角脈沖載荷作用時間的增加而增加，與準靜壓峰值無關。若ur,max出現在載荷分界點處，則ur,max與三角脈沖峰值成正比，與準靜壓峰值無關。若ur,max出現在準靜壓階段，當準靜壓與三角脈沖峰值之比λ 為定值時，則ur,max與三角脈沖峰值成正比；當三角脈沖峰值為定值時，隨著λ 的增大ur,max也增大。

（3）三角脈沖峰值、準靜壓以及TL均對準靜壓階段彈性等幅振動的振幅變化規律有影響，導致其具有不同的單調變化區域。