近距離爆炸比例爆距的界定標準及荷載模型*

甘 露，陳 力，宗周紅，錢海敏

（東南大學爆炸安全防護教育部工程研究中心，江蘇 南京 211189）

炸藥爆轟是一種高速進行的能自行傳播的化學變化過程，此過程會生成爆轟產物，并對周圍介質做功或形成壓力突躍狀態的傳播（沖擊波）。炸藥在空氣自由場近距離爆炸情況下，由于爆轟產物（火球、高溫高壓氣體等）存在隨機性和不均勻性，且會與沖擊波共同作用，因此其荷載主要呈現兩個特征—多峰值和不均勻。目前，世界各國針對空氣沖擊波的計算已經提出了很多公式，適用和界定條件也各不相同，但對于近距離爆炸的計算仍存在很多爭論。

Brode[1]、Henrych 等[2]和Baker[3]分別給出了球形裝藥爆炸條件下空氣沖擊波入射和反射的計算公式。Kingery 等[4]在此基礎上以比例爆距為自變量，基于高階多項式的方法提出了球形TNT爆炸入射波和反射波的計算方法，相關研究成果以圖表形式在美軍UFC3-340-02規范[5]中呈現，該成果已在防護工程設計和建設中得到了廣泛應用。但Shin 等[6-8]和Karlos等[9]的研究均認為UFC3-340-02對于近距離爆炸的計算未考慮爆轟產物的影響，不適用于近距離爆炸荷載預測。Shin 等[6]使用AUTODYN對比例爆距在0.053 1～40 m/kg1/3范圍內的自由場爆炸進行了模擬計算，提出了比例爆距與空氣沖擊波關鍵參數的關系曲線。Karlos等[9]基于EUROPLEXUS也進行了爆炸沖擊波相關參數的模擬計算，與文獻[6]類似地提出了新的多項式預測公式。

近距離爆炸范圍如何界定也是防護工程領域廣泛關注的問題，ASCE 59-11[10]認為比例爆距小于1.2 m/kg1/3范圍內的爆炸均屬于近距離爆炸。而Brode[1]及寧建國等[11]指出我國規范中爆炸荷載計算公式推薦的適用范圍為比例爆距大于1 m/kg1/3。胡攀[12]研究近距離爆炸下建筑結構上的爆炸荷載，同樣以1 m/kg1/3作為近距離爆炸和遠距離爆炸的區分界限。Orton 等[13]在研究中引用了UFC 3-340-02對于近距離爆炸的界定標準，將比例爆距小于0.40 m/kg1/3界定為近距離爆炸，比例爆距大于1 m/kg1/3界定為遠距離爆炸。李臻等[14]認為比例爆距0.40 m/kg1/3以上為中遠距離爆炸，中遠距離爆炸造成的結構破壞主要由空氣沖擊波導致，而不是爆轟產物導致。汪維等[15]對受近距離爆炸作用的方形板荷載分布函數進行了研究，他們將比例爆距0.25～2 m/kg1/3的范圍界定為近距離爆炸。可以看出，目前對于近距離爆炸的比例爆距界定均基于學者的工程或試驗經驗，學者之間的研究結論并不統一，甚至相互矛盾，且缺乏系統的機理性分析和理論支撐。

本文中基于LS-DYNA 建立精細化有限元分析模型，并將模型計算結果與規范進行對比驗證；基于經過驗證的精細化模型，探討TNT球形裝藥自由場爆炸沖擊波傳播與爆轟產物高速膨脹共同作用的特點和規律，分析近距離爆炸情況下剛性壁面上爆炸荷載的分布特征，并對近距離爆炸的比例爆距范圍進行定量界定；提出適用于近距離爆炸工況的剛性壁面反射荷載計算公式，確定爆炸荷載分布的上下限。

1 球形裝藥爆炸有限元模型的建立與驗證

1.1 有限元模型的建立

基于LS-DYNA 建立了包括TNT球形炸藥和空氣的自由場2D軸對稱計算模型，如圖1所示。選取1 kg 裝藥進行計算，并根據FEMA453[16]選取了背心炸彈和箱包炸彈兩種典型的裝藥質量進行對比驗證，分別為9 kg（20 lbs）和23 kg（50 lbs）。1、9、23 kg 裝藥的計算模型尺寸分別為120 cm×120 cm，250 cm×250 cm 和340 cm×340 cm。TNT炸藥和空氣采用Multi-material ALE算法的ALE2D單元進行模擬，模型邊界條件包括軸對稱邊界、鏡像對稱邊界和無反射邊界（見圖1），模型網格劃分如圖2所示，TNT炸藥及附近空氣網格采用漸變網格，其余空氣網格采用均勻網格劃分。

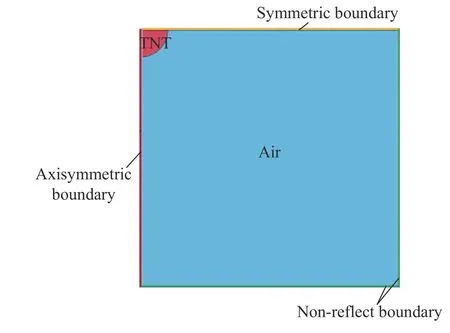
圖1 2D軸對稱模型Fig.1 2D axisymmetric model

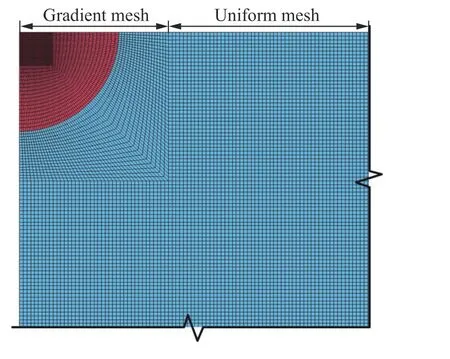
圖2 有限元網格劃分Fig.2 Mesh of the finiteelement model

1.2 材料模型

1.2.1 TNT炸藥

炸藥材料模型采用LS-DYNA 中的*MAT_HIGH_EXPLOSIVE_BURN進行描述，炸藥的狀態方程采用Jones-Wilkins-Lee(JWL)方程進行描述：

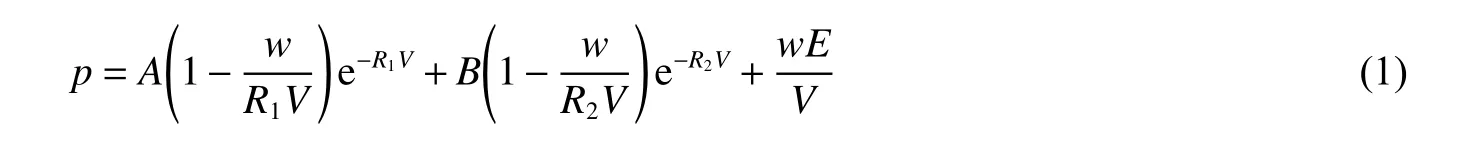
式中：A、B、w、R1、R2為與炸藥特性相關的參數，V為相對體積。炸藥材料模型及狀態方程參數采用Dobratz 等[17]提出的參數，參數值見表1。

表1 炸藥模型參數[17]Table 1 Parameters for modeling TNT explosive[17]

1.2.2空氣

空氣采用LS-DYNA 中的*MAT_NULL 材料模型描述，并使用*EOS_LINER_POLYNOMIAL 狀態方程：

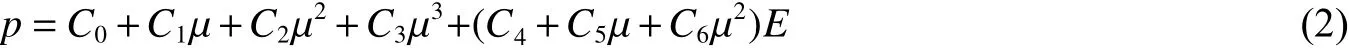
式中：C0、C1、C2、C3、C4、C5、C6為自定義系數；μ=ρ/ρ0?1，ρ/ρ0為當前空氣密度與參考空氣密度之比；E為單位參考體積的初始能量。其材料模型參數及狀態方程參數見表2。

表2 空氣模型參數Table 2 Parameters for modeling air

1.3 計算網格尺寸的確定

分別開展了3種質量（1、9、23 kg）裝藥的數值試驗，并對這3種質量裝藥分別進行了網格尺寸收斂性分析。3種炸藥的半徑分別為5.27、11.00、15.00 cm。1 kg 炸藥采用了1.00、2.00、4.00 mm 等3種網格尺寸進行比較計算，9 kg 炸藥采用了1.50、3.00、6.00 mm 等3種網格尺寸，23 kg炸藥采用了2.50、5.00、10.00 mm 等3種網格尺寸。計算出的自由場超壓峰值如圖3所示，并與UFC 3-340-02的計算結果及其正負誤差10%進行對比。

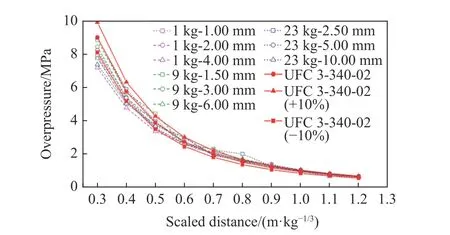
圖3 不同網格尺寸情況下超壓峰值與比例爆距的關系Fig.3 Peak overpressure versusscaled distances with different mesh sizes

由圖3可知，比例爆距大于0.60 m/kg1/3時，所有裝藥情況下不同網格尺寸模型的計算結果誤差幾乎全部在UFC 3-340-02計算值的10%以內。但當比例爆距小于0.60 m/kg1/3時，所有裝藥情況下，4.00、6.00、10.00 mm 網格尺寸模型的計算誤差均超出10%。因此，為了保證計算結果的準確性并兼顧計算效率，1、9、23 kg 裝藥模型的網格尺寸分別確定為2.00、3.00、5.00 mm，這些網格尺寸大小均處于相對應的炸藥半徑的1/40～1/25范圍內。

1.4 有限元模型驗證

UFC3-340-02[5]給出了球形TNT 裝藥在不同比例爆距下的自由場入射超壓及剛性反射超壓計算圖。Shin[7]計算發現，UFC 3-340-02中的自由場入射超壓及正反射超壓計算圖在比例爆距大于0.4 m/kg1/3時較為準確。本文中選取UFC 3-340-02公式進行對比驗證，建立的有限元模型包含炸藥、空氣和剛體，剛體采用關鍵字*MAT_RIGID模擬，流固耦合采用*CONSTRAINED_LAGRANGE_IN_SOLID關鍵字進行描述，驗證計算了1、9、23 kg 等3種裝藥工況。自由場入射超壓峰值的計算結果與UFC 3-340-02對比如圖4所示，正反射超壓峰值的計算結果對比如圖5所示。

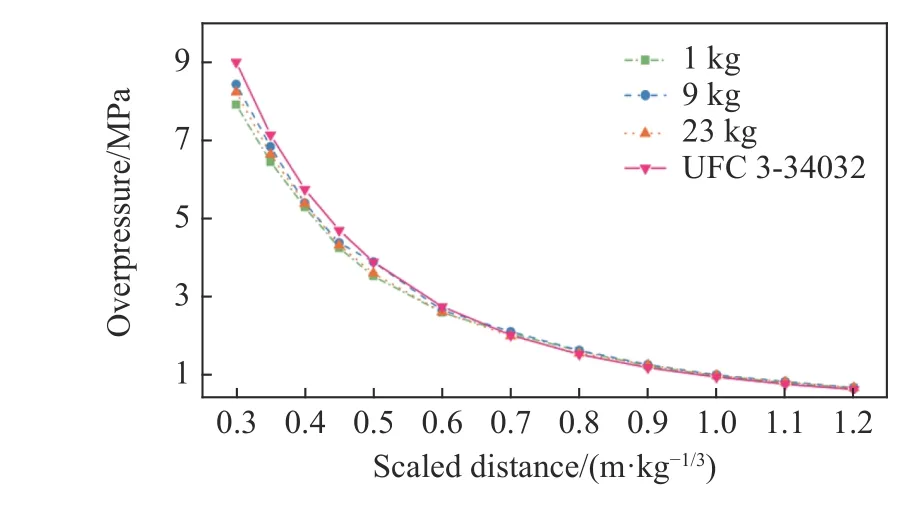
圖4 自由場超壓峰值與比例爆距的關系Fig.4 Incident free-field overpressures versus scaled distances

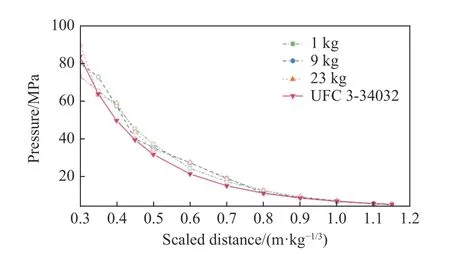
圖5 正反射超壓峰值與比例爆距的關系Fig.5 Reflected overpressures versus scaled distances

由圖4～5可以看出，建立的有限元模型計算結果與UFC 3-340-02吻合較好，在比例爆距大于0.30 m/kg1/3范圍內計算結果可信。

2 近距離爆炸比例爆距范圍的界定

2.1 空氣沖擊波傳播與爆轟產物高速膨脹機理

炸藥的JWL狀態方程能夠準確地描述爆轟產物的膨脹過程[18]，且該狀態方程對爆轟產物模擬的準確性在試驗中得到了驗證[19]。基于已經驗證的數值模型，計算出了球形TNT 爆炸產生的沖擊波傳播及爆轟產物膨脹的過程，如圖6所示，爆炸時爆轟產物高速膨脹，并強烈壓縮周邊空氣；在比例爆距小于0.30 m/kg1/3范圍內，爆轟產物與空氣界面清晰和平滑（見圖6(a)）；當比例爆距達到0.35 m/kg1/3左右時，爆轟產物與空氣界面開始變得不平滑（見圖6(a)）；當比例爆距達到0.50 m/kg1/3左右時，出現了明顯的湍流效應（見圖6(b)），且隨著比例爆距的不斷增大，湍流效應越來越顯著；如圖6(c)～(d)所示，在比例爆距達到0.80 m/kg1/3左右時，爆轟產物達到最大膨脹體積，且由于負壓作用，爆轟產物開始回縮。文獻[11]中的研究結果顯示，當距離為10～15 倍炸藥半徑時，空氣沖擊波與爆轟產物開始緩慢分離，本文計算結果與此段描述一致。

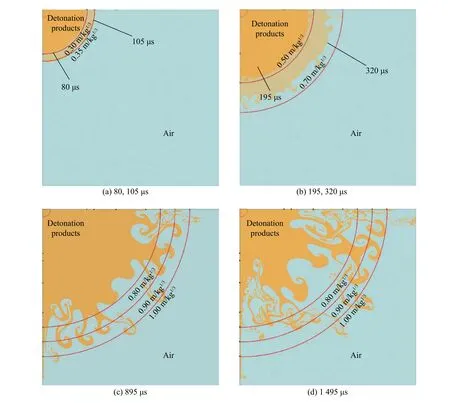
圖6 爆轟產物膨脹過程Fig.6 Expansion of detonation products

2.2 剛性壁面正反射荷載規律

分別針對1、9、23 kg 等3種裝藥，開展12種比例爆距工況的爆炸荷載計算，比例爆距范圍為0.30～1.20 m/kg1/3。

以1 kg TNT爆炸為例，選取比例爆距分別為0.30、0.50、0.85、1.00、1.20 m/kg1/3的5條正反射超壓曲線（見圖7）進行分析比較。如圖7(a)所示，在比例爆距為0.30、0.50 m/kg1/3時，反射超壓曲線呈現出與文獻[20]實測結果相似的多峰值現象，且第2個峰值明顯大于第1個峰值。在比例爆距為0.30 m/kg1/3時，兩個峰值出現的時間相差較短，而比例爆距為0.50 m/kg1/3時，2 個峰值（見圖7（a））分別出現在166、194μs時刻，時間相差較大。

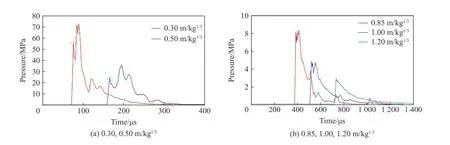
圖7 5種比例爆距工況的剛體反射超壓曲線Fig.7 Reflected overpressure curvesat fivetypes of scale distances

如圖8～9所示，當剛體位于0.50 m/kg1/3比例爆距位置時，沖擊波在166μs時刻先于爆轟產物到達剛體表面發生反射，對應圖7(a)中的第1 個波峰；隨后爆轟產物在194μs時刻到達剛體表面，對應圖7(a)中的第2個波峰。圖9給出了不同比例爆距時空氣沖擊波和爆轟產物的到達時間以及對應的剛體表面荷載峰值。對比圖7（b）和圖9可以看出，比例爆距為0.85、1.00 m/kg1/3時，反射超壓曲線依然存在多峰現象，但是比例爆距為0.85 m/kg1/3時，反射沖擊波荷載峰值與爆轟產物荷載峰值大小相當。當比例爆距為1.00 m/kg1/3時，沖擊波反射荷載峰值大于爆轟產物荷載峰值。當比例爆距為1.20 m/kg1/3時，剛體上的爆炸荷載曲線只存在一個由空氣沖擊波反射引起的峰值，爆轟產物不再影響結構上的爆炸荷載。

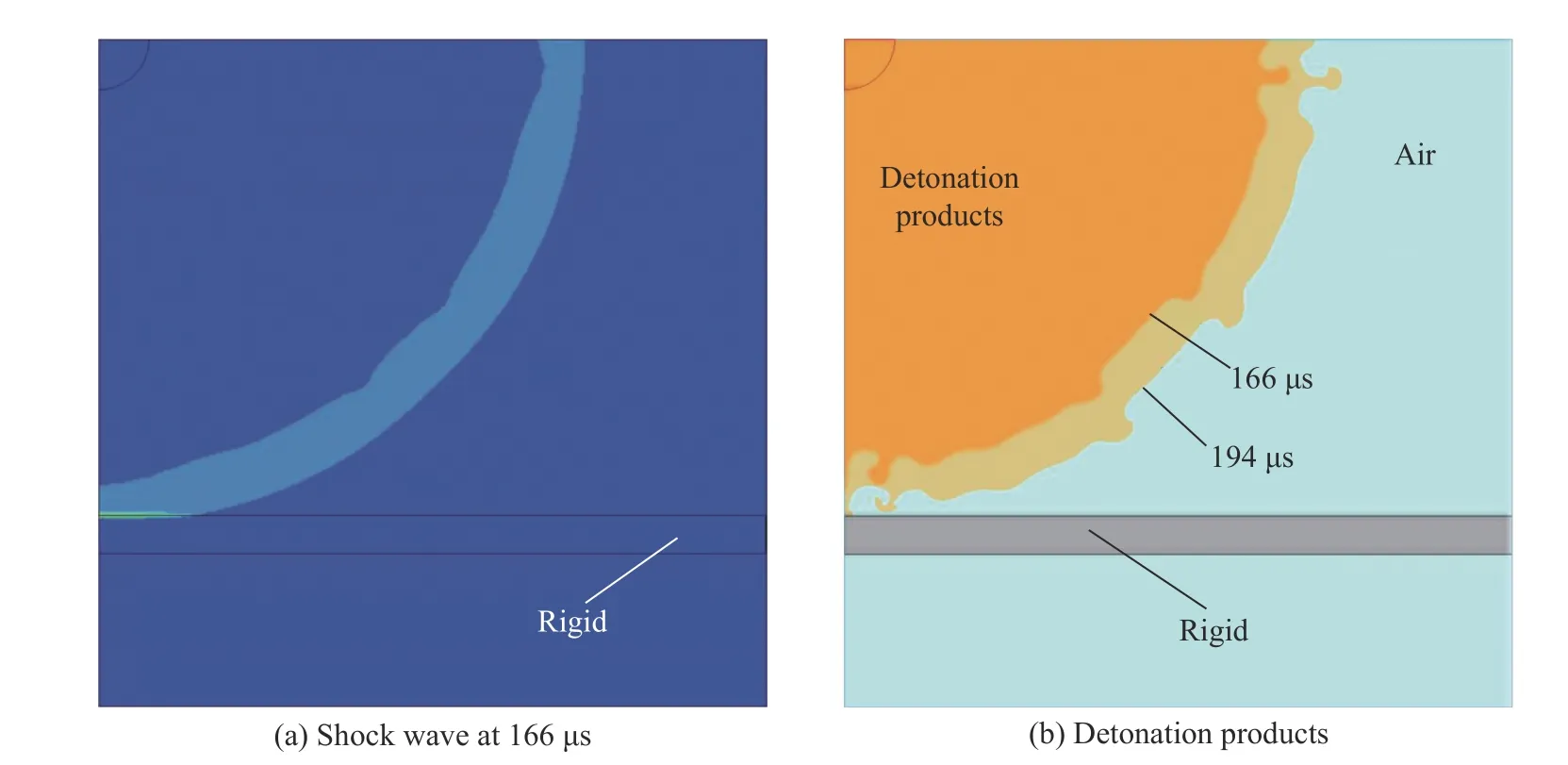
圖8 0.50 m/kg1/3比例爆距工況下沖擊波反射與爆轟產物撞擊作用現象Fig.8 Reflection of blast wave and detonation product at 0.50 m/kg1/3

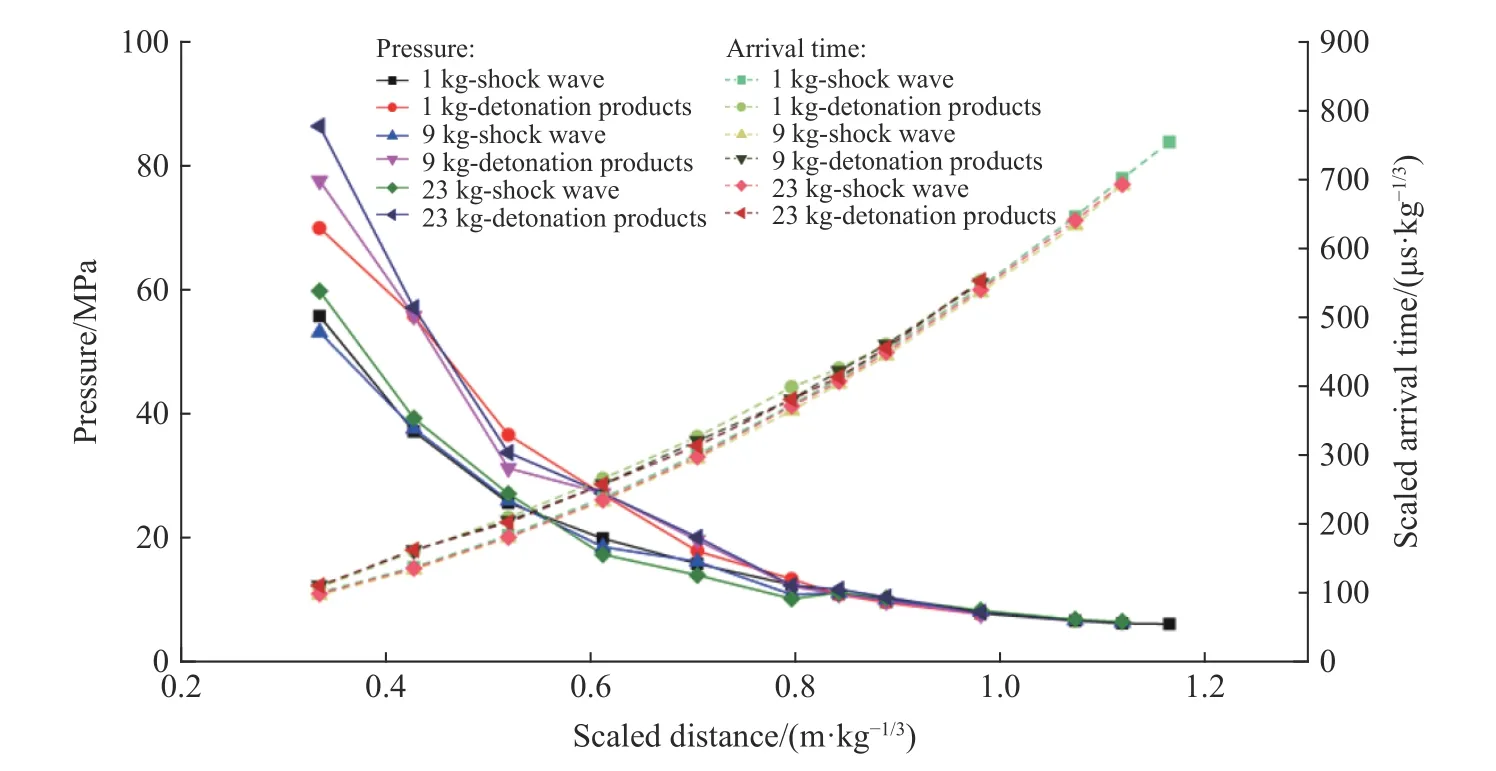
圖9 沖擊波與爆轟產物到達時間及荷載峰值Fig.9 Scaled arrival times and peak pressures of shock wave and detonation products

2.3 近距離爆炸剛性壁面荷載分布規律

爆炸荷載分布對結構的動力響應影響很大。針對不同比例爆距工況，選取1、9、23 kg 當量的TNT分別計算近距離爆炸下剛性壁面的荷載分布。由UFC 3-340-02可知，在40°～60°范圍內，反射會受到馬赫反射影響。因此，為避免馬赫反射的影響，荷載分布計算的入射角取為α=0°～40°（見圖10）。

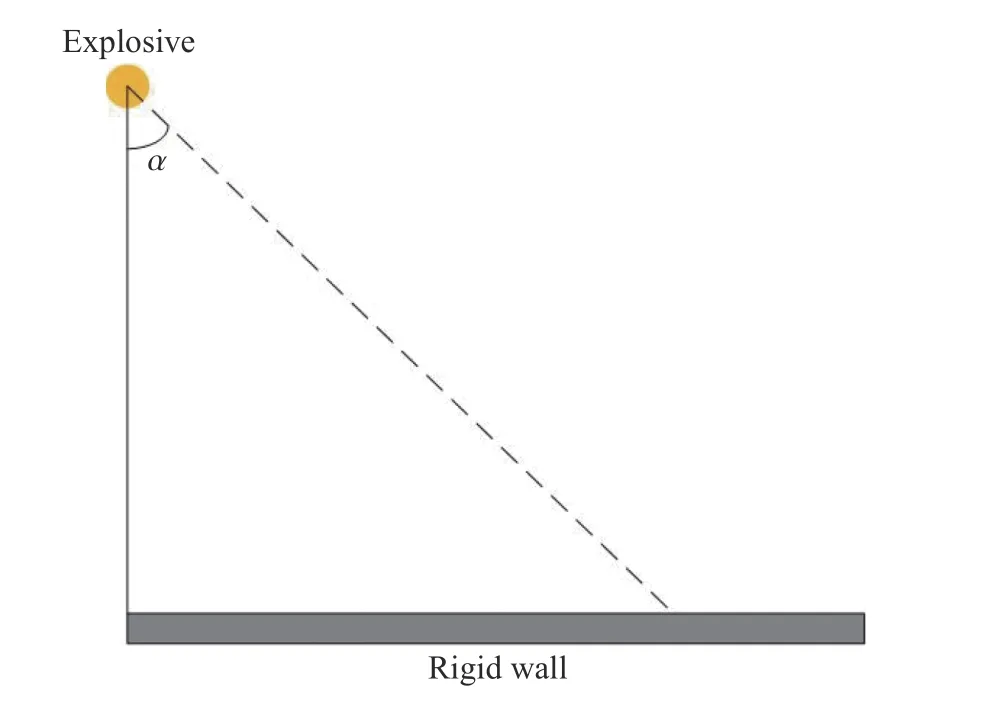
圖10 板面荷載計算范圍Fig.10 Calculated scopeof load distribution

以正反射（入射角α=0°）荷載超壓峰值為基準，對不同入射角激發的反射超壓荷載峰值進行歸一化處理，即：

式中：pα為α 入射角對應的反射超壓峰值，p0為正反射超壓峰值。

計算結果如圖11所示，當比例爆距在0.30～0.80 m/kg1/3范圍內時，爆炸荷載在α=0°～5°范圍內急劇下降。主要原因在于0.30～0.80 m/kg1/3范圍內爆轟產物噴射不均勻。如圖6所示，爆轟產物在0.35 m/kg1/3時開始出現邊界不平滑現象，而比例爆距小于0.35 m/kg1/3時，爆轟產物呈球面規則擴散。因此，當比例爆距為0.30 m/kg1/3時，爆炸荷載峰值在入射角α=0°～5°范圍內的下降幅度明顯小于比例爆距0.35～0.80 m/kg1/3范圍內的下降幅度。而比例爆距大于0.80 m/kg1/3時，爆轟產物幾乎達到最大膨脹體積，爆轟產物對剛性壁面荷載的影響減小。因此，比例爆距大于0.80 m/kg1/3時，爆炸荷載在剛性壁面上的分布也較為均勻，在入射角α=0°～5°范圍內未出現荷載峰值急劇下降的現象。

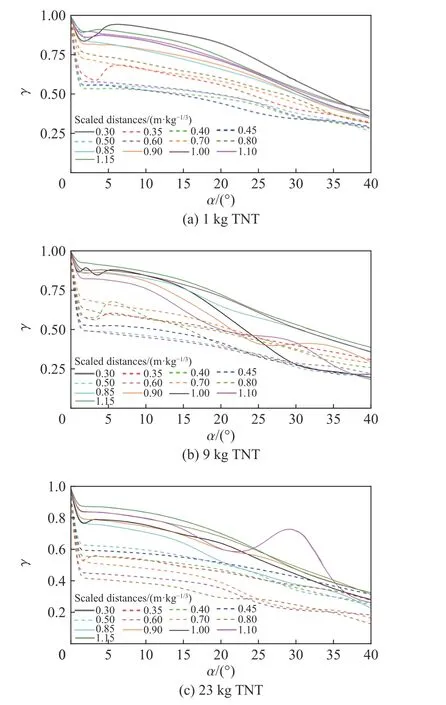
圖11 不同比例爆距工況下剛性壁面荷載峰值分布Fig.11 Load distributions at different types of scaledistances

在0.30～1.20 m/kg1/3范圍內，剛性壁面爆炸荷載可以分為2 個比例爆距區，即0.30～0.80 m/kg1/3和0.80～1.20 m/kg1/3。比例爆距在0.30～0.80 m/kg1/3內，入射角α=0°～5°范圍內的剛性壁面荷載峰值相對于正反射荷載峰值下降25%～60%；比例爆距大于0.80 m/kg1/3時，入射角α=0°～5°范圍內的剛性壁面荷載峰值相對于正反射荷載峰值下降幅度小于20%。

2.4 近距離爆炸的比例爆距界定

通過以上計算分析可以發現，當比例爆距在0.30～0.80 m/kg1/3的范圍內時，空氣沖擊波將先于爆轟產物到達結構表面，結構表面荷載存在多個峰值，且沖擊波反射荷載的峰值小于爆轟產物荷載峰值，結構上的爆炸荷載受爆轟產物的影響較為顯著。

受爆轟產物噴射隨機性和不均勻性的影響，當比例爆距在0.30～0.80 m/kg1/3范圍內時，剛性壁面荷載峰值在入射角0°～5°范圍內急劇下降；當比例爆距大于0.80 m/kg1/3時，爆轟產物對壁面爆炸荷載的影響降低，直至在比例爆距大于1.20 m/kg1/3時，爆轟產物幾乎無影響，壁面荷載峰值由空氣沖擊波決定。因此，當比例爆距大于0.80 m/kg1/3時，入射角0°～5°范圍內的荷載峰值突降現象不顯著，剛性壁面爆炸荷載分布開始趨于平滑。

對于球形TNT爆炸，比例爆距等于0.30 m/kg1/3時，爆轟產物與空氣沖擊波幾乎同時到達結構表面。當比例爆距小于0.30 m/kg1/3時，爆轟產物先于沖擊波到達，受此影響，此時理想氣體狀態方程也已不能用于描述空氣的壓力與體積關系；且在高壓環境下，空氣的不定常特征更顯著[21]，本文中的模型已不適用于討論比例爆距小于0.30 m/kg1/3工況下的爆炸荷載。因此，考慮爆轟產物的影響，綜合分析自由場沖擊波入射超壓峰值、剛性壁面爆炸荷載峰值及分布規律后，建議將比例爆距0.30～0.80 m/kg1/3范圍內的爆炸定義為近距離爆炸，將比例爆距0.80～1.20 m/kg1/3范圍內的爆炸定義為中距離爆炸，將比例爆距大于1.20 m/kg1/3范圍的爆炸定義為遠距離爆炸。

3 近距離爆炸剛性壁面荷載模型

3.1 剛性壁面近距離爆炸正反射荷載計算模型

在近距離爆炸的比例爆距范圍內，剛性壁面正反射荷載時程曲線上存在由沖擊波和爆轟產物分別引起的2個峰值，因此，可以將爆炸荷載分為沖擊波反射荷載和爆轟產物荷載分別計算。

3.1.1沖擊波荷載模型

（1）沖擊波峰值

分別對1、9、23 kg 炸藥爆炸情況下，剛性壁面沖擊波正反射荷載峰值數據進行擬合，采用了負次冪函數、指數函數和多項式函數3種擬合公式：

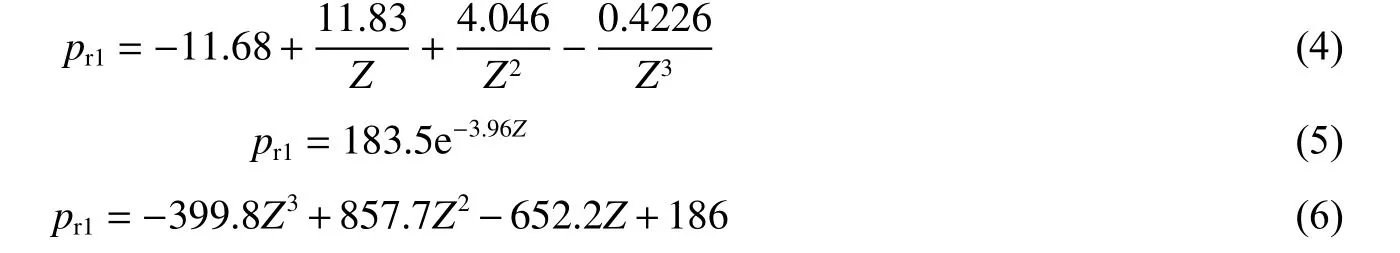
式中：pr1為沖擊波正反射超壓峰值，MPa；Z為比例爆距，m/kg1/3。

擬合結果如圖12所示，可以發現3種公式的擬合程度均較高，式（4）～（6）擬合優度均大于0.99。考慮到UFC 3-340-02采用的荷載預測公式為多項式形式，為方便計算，本文中也推薦采用擬合出的多項式公式進行峰值計算。

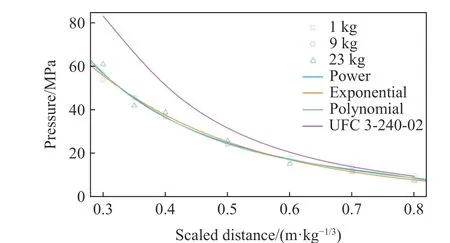
圖12 沖擊波正反射超壓峰值擬合曲線（0.30 m/kg1/3＜Z≤0.80 m/kg1/3）Fig.12 Fitting curveof peak normal reflected overpressures of shock waves (0.3 m/kg1/3＜Z≤0.8 m/kg1/3)

（2）沖擊波到達時間

將比時間定義為：

式中：t為比時間，μs/kg1/3；ta為真實時間，μs；W為TNT的質量，kg。

采用多項式函數對1、9、23 kg 的沖擊波到達比時間數據進行擬合：

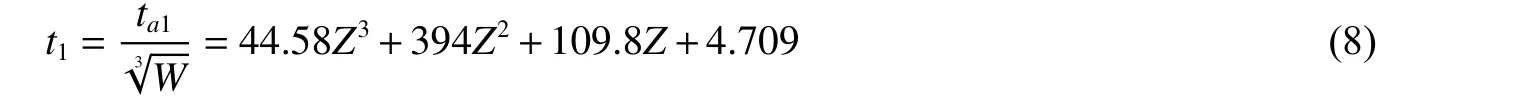
式中：t1為沖擊波到達比時間，ta1為沖擊波到達真實時間。擬合關系如圖圖13所示。

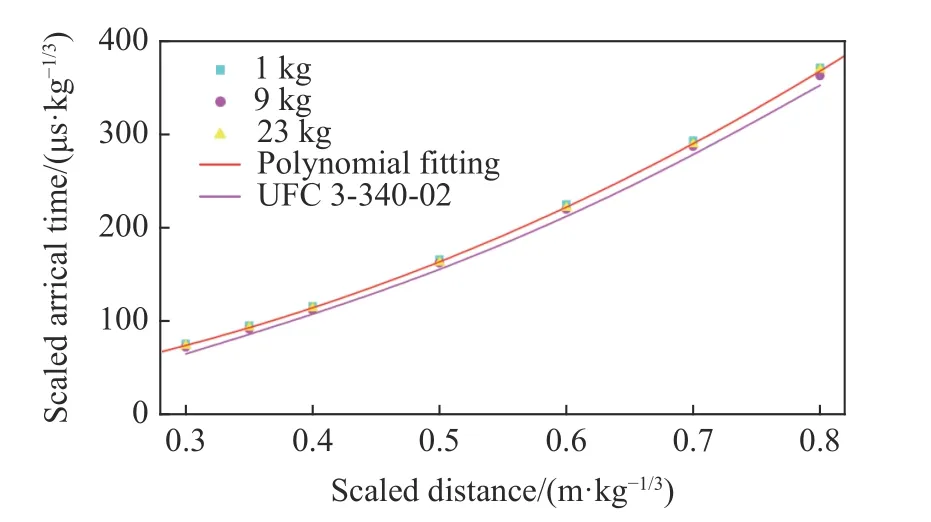
圖13 沖擊波到達比時間擬合曲線（0.30 m/kg1/3＜Z≤0.80 m/kg1/3）Fig.13 Fitting curve of scaled arrival times of shock waves(0.30 m/kg1/3＜Z≤0.80 m/kg1/3)

如圖12～13所示，由于未能具體區分沖擊波和爆轟產物的各自影響，UFC 3-340-02計算出的荷載峰值顯著大于本文中計算出的沖擊波反射引起的荷載峰值，且比例爆距越小，差距越大，差距的產生正是由于爆轟產物對爆炸荷載的影響；UFC 3-340-02的荷載到達比時間與本文計算出的沖擊波到達比時間較吻合，而這進一步支撐了近距離爆炸情況下沖擊波要早于爆轟產物到達的結論。

3.1.2爆轟產物荷載模型

（1）爆轟產物峰值

采用與沖擊波峰值相同的公式進行爆轟產物荷載峰值擬合：

擬合曲線如圖14所示，可以發現在0.30 m/kg1/3＜Z≤0.80 m/kg1/3范圍內，三種曲線擬合精度均較高。為與UFC 3-340-02統一，建議采用下式進行荷載計算：

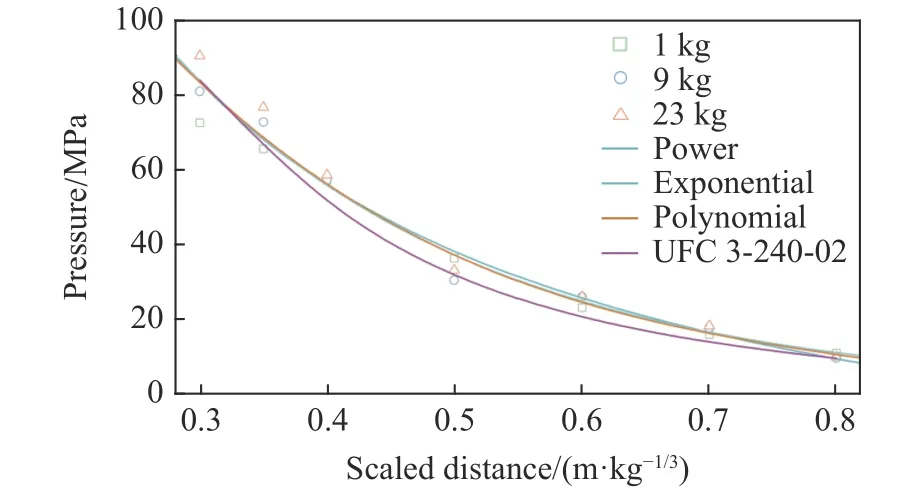
圖14 爆轟產物荷載峰值擬合曲線（0.30 m/kg1/3＜Z≤0.80 m/kg1/3）Fig.14 Fitting curve of peak overpressures of detonation products (0.30 m/kg1/3＜Z≤0.80 m/kg1/3)

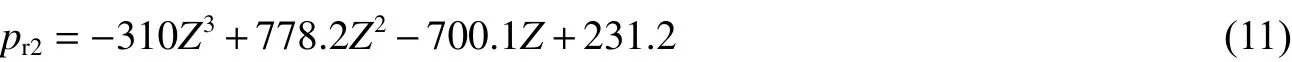
式中：pr2為爆轟產物作用引起的荷載峰值，MPa。

（2）爆轟產物到達時間

爆轟產物到達比時間擬合結果如圖15所示，擬合公式如下：

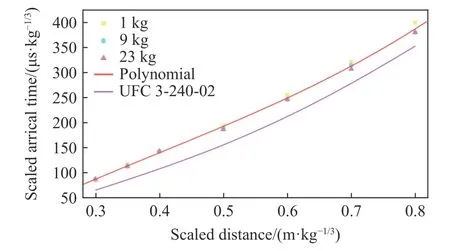
圖15 爆轟產物到達比時間擬合曲線（0.30 m/kg1/3＜Z≤0.80 m/kg1/3）Fig.15 Fitting curve of scaled arrival times of detonation products (0.30 m/kg1/3＜Z≤0.80 m/kg1/3)

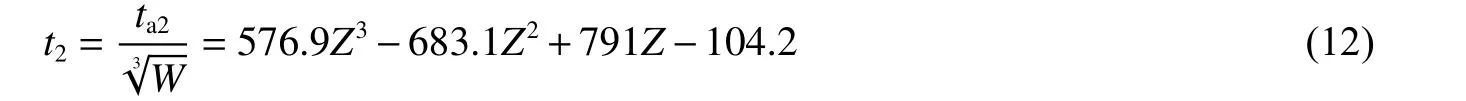
式中：t2為爆轟產物到達比時間，ta1為爆轟產物到達真實時間。

將荷載峰值和到達時間的擬合結果與UFC 3-340-02結果進行對比，發現UFC 3-340-02給出的荷載峰值與計算得到的爆轟產物荷載峰值相近，且比例爆距越小，差距越小；這更加說明了近距離爆炸情況下爆轟產物產生的荷載是爆炸荷載的主要影響因素；而UFC 3-340-02給出的荷載到達比時間顯著小于計算出的爆轟產物到達比時間，同樣支撐了近距離爆炸情況下，沖擊波要先于爆轟產物到達的結論。

3.1.3比沖量模型

比沖量數據擬合結果如圖16所示，擬合公式如下：

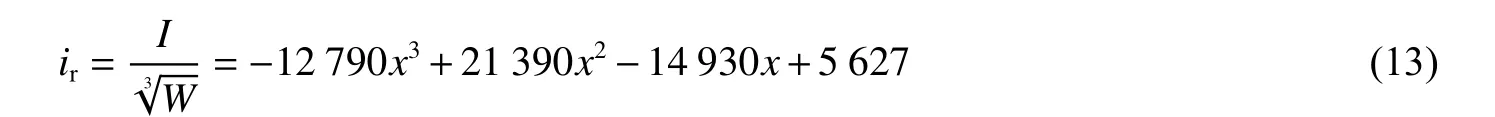
式中：ir為比沖量，Pa·ms/kg1/3；I為沖量，Pa·ms。

由圖16可知，比沖量擬合數據比UFC 3-340-02給出的結果偏大，這是由如圖7所示的荷載多峰值現象導致的。

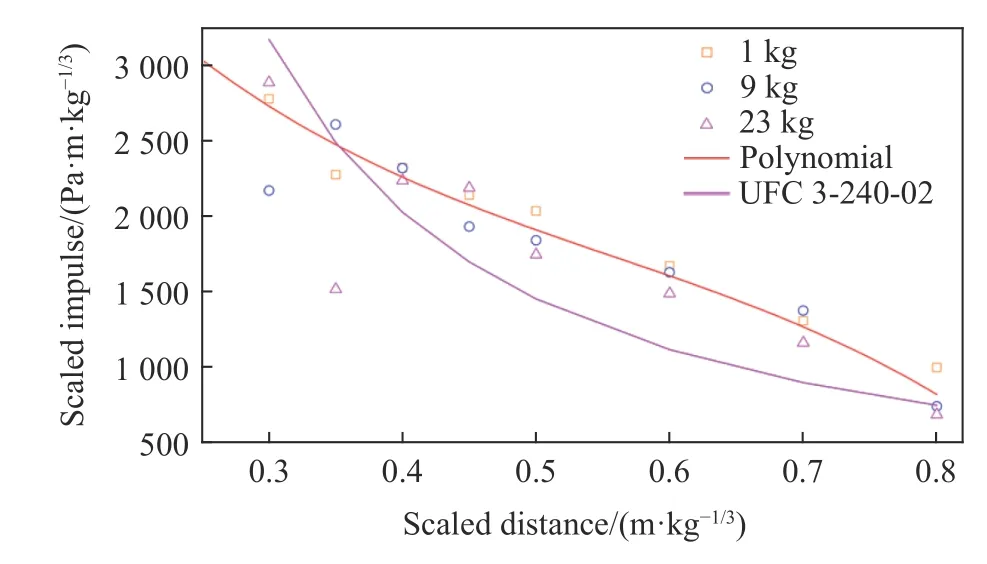
圖16 比沖量結果曲線（0.30 m/kg1/3＜Z≤0.80 m/kg1/3）Fig.16 Scaled impulses fitting curvesfor 0.30 m/kg1/3＜Z≤0.80 m/kg1/3

3.1.4近距離爆炸荷載簡化計算模型

對于受爆炸荷載作用的工程結構，需要提出簡化模型以進行結構響應計算。針對近距離爆炸沖擊波與爆轟產物共同作用的特點，提出了剛性壁面近距離爆炸荷載簡化計算模型，示意圖如圖17所示。

采用與UFC 3-340-02相同的等沖量方法進行荷載結束時刻t3的計算：

因此，基于擬合公式（6）、（8）、（11）～（12）、（14），本文中提出的近距離爆炸荷載簡化計算模型可以用分段函數表示為：

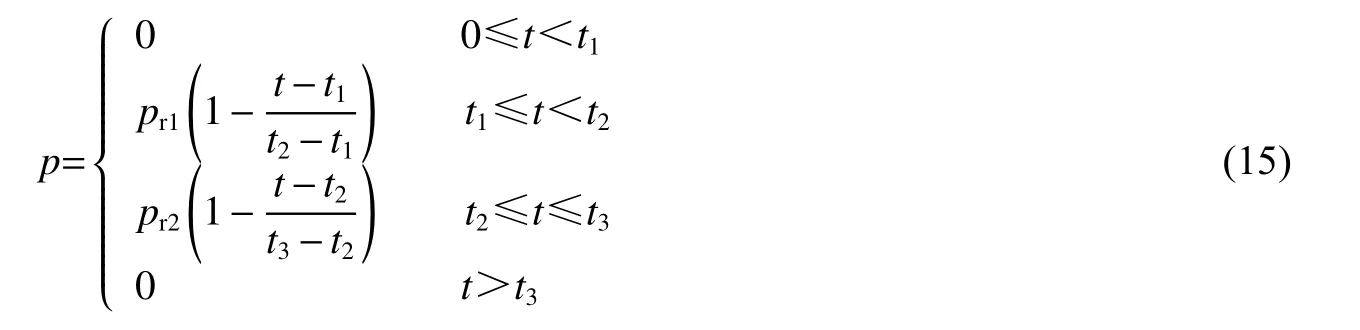
3.2 剛性壁面近距離爆炸荷載峰值分布

根據前述近距離爆炸的比例爆距界定標準，根據式（3）可將結構壁面荷載以正反射為基準進行歸一化處理。并以入射角α 的正切值為橫坐標，將0.30 m/kg1/3＜Z≤0.80 m/kg1/3比例爆距范圍內的所有數據和比例爆距大于0.80 m/kg1/3范圍內的所有數據分別進行包絡，得到剛性壁面荷載峰值分布區間，如圖18所示。

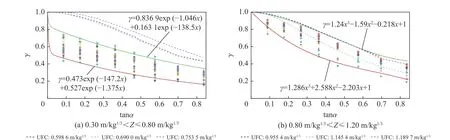
圖18 剛性壁面荷載分布區間Fig.18 Distribution of blast loadson rigid walls

近距離爆炸下，入射角0°～40°范圍內的壁面爆炸荷載峰值范圍可表示為：

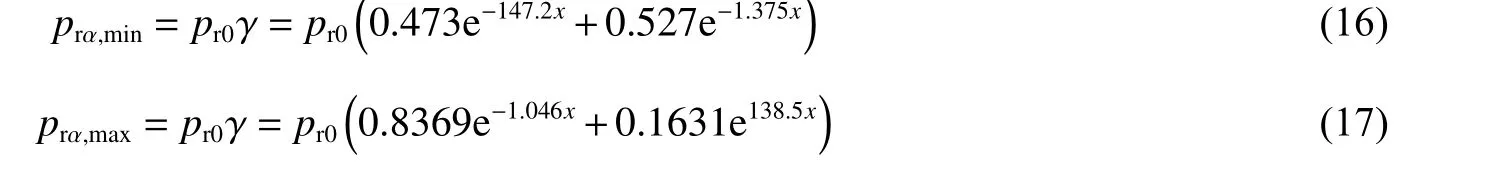
式中：prα,min為α 角度處荷載峰值下限；prα,max為α 角度處荷載峰值上限；x=Tanα。

中距離爆炸下，入射角0～40°范圍內的壁面爆炸荷載峰值范圍可表達為：

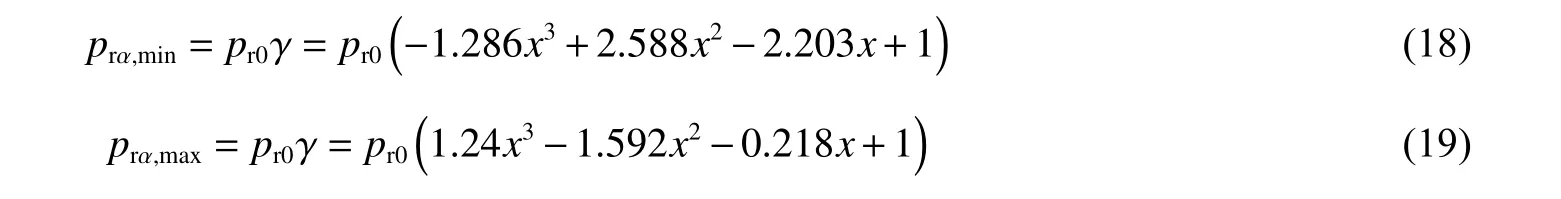
圖18中同時給出了與UFC 3-340-02數據的比較，可以發現，對于近距離爆炸，由于爆轟產物噴射分布的影響，計算出的剛性壁面荷載峰值分布與UFC 3-340-02給出的數據差距較大，這主要是因為現有模型尚不能全面考慮爆轟產物噴射的隨機性，尚需要改進，而UFC 3-340-02則是基于大量實驗數據進行包絡擬合的結果，UFC 3-340-02數據更偏于安全和可靠。但對于比例爆距在0.80 m/kg1/3＜Z≤1.20 m/kg1/3范圍內的爆炸工況，由于爆轟產物的影響較小，沖擊波作用的貢獻占主導地位，UFC 3-340-02給出的剛性壁面荷載分布位于本文計算結果的上下限范圍內，同樣證明了本文結果的可靠性。

4 結 論

基于LS-DYNA 平臺建立了精細化有限元模型并通過了嚴格的模型驗證，研究了球形TNT裝藥爆轟產物對剛性壁面正反射爆炸荷載和壁面荷載峰值分布的影響規律，提出了近距離爆炸、中距離爆炸和遠距離爆炸的界定準則。分別給出了剛性壁面沖擊波荷載峰值和爆轟產物荷載峰值的計算公式，提出了近距離爆炸剛性壁面爆炸荷載簡化計算模型。主要結論有。

（1）近距離爆炸下，爆炸荷載由爆轟產物和沖擊波共同作用產生，受爆轟產物噴射不均勻性和隨機性的影響，爆炸荷載在所作用的結構上呈現高度的不均勻分布；

（2）近距離爆炸下，空氣沖擊波將先于爆轟產物到達結構表面，結構表面荷載存在多個峰值，且沖擊波反射荷載的峰值小于爆轟產物荷載峰值，結構上的爆炸荷載受爆轟產物的影響較為顯著。中距離爆炸下，爆轟產物對壁面爆炸荷載的影響降低。遠距離爆炸下，爆轟產物幾乎無影響，壁面荷載峰值由空氣沖擊波決定；

（3）球形裝藥下，比例爆距在0.30 m/kg1/3＜Z≤0.80 m/kg1/3范圍內定義為近距離爆炸，比例爆距在0.80 m/kg1/3＜Z≤1.20 m/kg1/3范圍內定義為中距離爆炸，比例爆距大于1.20 m/kg1/3定義為遠距離爆炸。