平動非慣性質(zhì)心參考系動力學(xué)規(guī)律的應(yīng)用

劉傳躍

(鄒平市第一中學(xué),山東 濱州 256200)

1 平動非慣性質(zhì)心參考系的動力學(xué)規(guī)律

如圖1所示,建立固連于地面的靜止慣性參考系S,以質(zhì)點系統(tǒng)的質(zhì)心為原點建立質(zhì)心參考系S′.當(dāng)質(zhì)心參考系S′具有平動加速度aC時,則該系稱為平動非慣性質(zhì)心參考系.

圖1 平心非慣性質(zhì)心參考系

下面討論在平動非慣性質(zhì)心參考系中的動力

學(xué)規(guī)律.

1.1 質(zhì)點的動力學(xué)方程

對質(zhì)點系統(tǒng)中第i個質(zhì)點,設(shè)其質(zhì)量為mi,則該質(zhì)點在質(zhì)心參考系中的動力學(xué)方程為

(1)

1.2 平動慣性力對質(zhì)心的力矩和作用點

第i個質(zhì)點受到的平動慣性力為fi=-miaC,其中aC為系統(tǒng)質(zhì)心的加速度.由此可知,每個質(zhì)點受到的平動慣性力的大小與其質(zhì)量成正比,方向均與質(zhì)心參考系的加速度aC反向.在質(zhì)心參考系中各質(zhì)點所受平動慣性力對以質(zhì)心為參考點的力矩矢量和為

MC′=∑(ri′×fi)=-∑(miri′)×aC=0,

即有

MC′=0.

(2)

該式說明,在平動非慣性質(zhì)心參考系中各質(zhì)點受到平動慣性力的合力矩為0.平動慣性力的合力f=-∑miaC不為0,其作用點為質(zhì)心,但并不意味著各質(zhì)點受到的慣性力矩不做功.

1.3 質(zhì)點系統(tǒng)的動能定理

在慣性參考系中對質(zhì)點系統(tǒng)考慮柯尼希定理,由動能定理,得

∑Fi外·dri+∑Fi內(nèi)·dri=

(3)

dri=drC+dri′,

(4)

式中dri′為第i個質(zhì)點在質(zhì)心參考系中的位移,將(4)式代入(3)式,得

∑Fi外·drC+∑Fi內(nèi)·drC+∑Fi外·dri′+

∑Fi內(nèi)·dri′=

(5)

利用該式消去(5)式左側(cè)第一項和右側(cè)第一項.若系統(tǒng)內(nèi)任意一對內(nèi)力作用點的相對位移為0,則會使該對內(nèi)力所做總功為0.因(5)式中左側(cè)第二項為系統(tǒng)內(nèi)力對質(zhì)心做功的代數(shù)和,故在任意參考系中該值為零.則(5)式最終為

∑Fi外·dri′+∑Fi內(nèi)·dri′=

即有

∑Ai外′+∑Ai內(nèi)′=∑ΔEk′.

該式說明,在質(zhì)心參考系中質(zhì)點系統(tǒng)總動能的增量,等于所有外力對各質(zhì)點所做的功與所有內(nèi)力對各質(zhì)點所做的功之和.這就是質(zhì)心參考系中質(zhì)點系統(tǒng)的動能定理.該式與慣性系中的系統(tǒng)的動能定理在形式上保持一致.

1.4 質(zhì)點系統(tǒng)的角動量定理

在慣性參考系中,系統(tǒng)相對于固定參考點O的角動量為

(6)

第i個質(zhì)點相對質(zhì)心的關(guān)系有

(7)

將(7)式代入(6)式,得

(8)

將(8)式對時間求導(dǎo),得

mrC×aC.

(9)

系統(tǒng)中各質(zhì)點受到的外力相對參考點O的力矩

∑Mi外=∑ri×Fi外=∑ri′×Fi外+

∑rC×Fi外=∑ri′×Fi外+mrC×aC.

(10)

由慣性參考系中的系統(tǒng)角動量定理

(11)

聯(lián)立(9)-(11)式,得

即有

(12)

該式表明,質(zhì)點系統(tǒng)對質(zhì)心的角動量的變化率,等于所有外力對質(zhì)心的合力矩.這就是質(zhì)心參考系中質(zhì)點系統(tǒng)對質(zhì)心的角動量定理.盡管質(zhì)心參考系不一定是慣性系,此式在形式上卻與慣性系中的角動量定理形式一樣.

2 平動非慣性質(zhì)心參考系的應(yīng)用

圖2 初始狀態(tài)

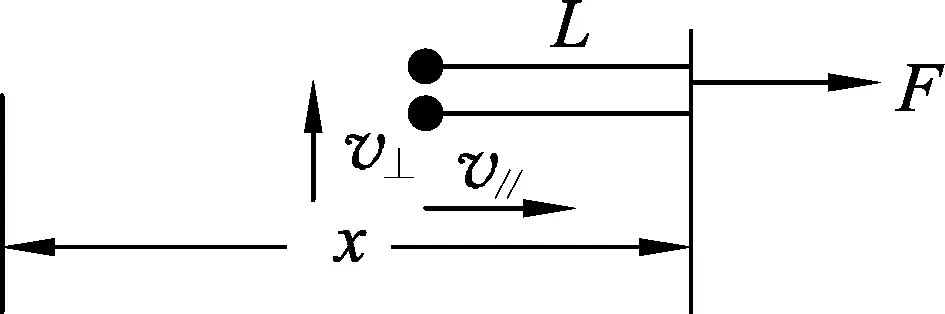
圖3 第1次相碰前瞬間

以上兩式涉及4個未知量,故求解需要尋找其他關(guān)系.又輕繩對兩小球做功W和沖量I在靜止參考系中不易求出,可考慮在平動非慣性質(zhì)心參考系中討論問題.

圖4 過程中的某個狀態(tài)

解答:以系統(tǒng)質(zhì)心C為原點建立平動非慣性質(zhì)心參考系,如圖4所示.設(shè)在過程中的某個狀態(tài),輕繩與豎直方向夾角為φ,在質(zhì)心參考系中質(zhì)心始終處于兩小球連線中點,由于質(zhì)心參考系為零動量參考系,故圖4中兩小球的速度等大反向.

以輕繩中點O′為研究對象,因其質(zhì)量為0故所受合力為0,有2Tsinφ=F,小球到質(zhì)心距離h=Lcosφ,取微分有dh=-Lsinφdφ,輕繩對兩小球的元功dW=2Tcosφdh,聯(lián)立以上各式得dW=-FLcosφdφ,對整個過程積分有

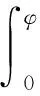
得輕繩對兩個小球做的總功為W=FLsinφ.

在質(zhì)心參考系中,對系統(tǒng)應(yīng)用動能定理,得

(1)

則有

(2)

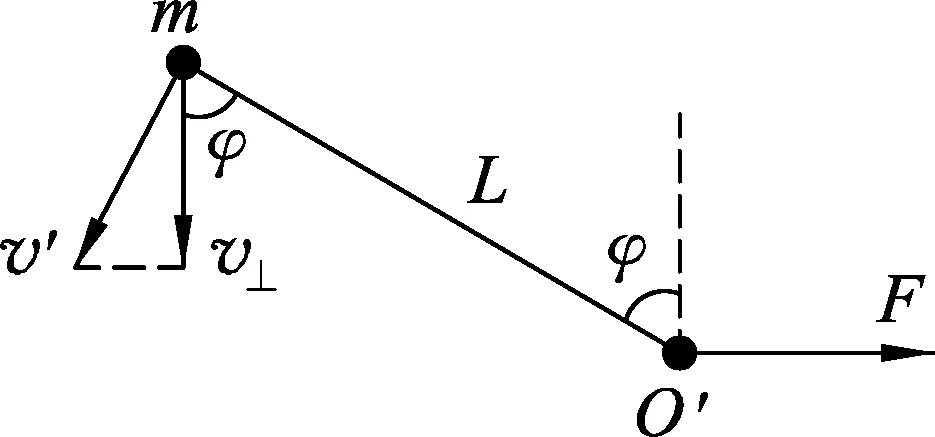
圖5 小球繞輕繩中點O′轉(zhuǎn)動

第1次相碰時φ=π/2,則有

(3)

如圖5所示,小球繞輕繩中點O′逆時針轉(zhuǎn)動,設(shè)夾角為φ時小球速度為v′,在質(zhì)心參考系中由速度合成定理,得

v′sinφ=v⊥，

(4)

在dt時間內(nèi)小球繞輕繩中點O′轉(zhuǎn)過角度dφ,則有

v′dt=Ldφ，

(5)

聯(lián)立(2)、(4)、(5)式,得

對整個過程積分,得

(6)

在靜止參考系中,對系統(tǒng)應(yīng)用動量定理,則有

Ft=2mv∥.

(7)

聯(lián)立(6)、(7)式,得

(8)

點評:解題的關(guān)鍵是在平動非慣性質(zhì)心參考系中的討論,一方面解決了輕繩對小球拉力做功的問題,另一方面將小球和輕繩中點O′之間的部分視為剛體,構(gòu)建小球繞中點O′的轉(zhuǎn)動模型,得出繞行過程的微分方程,通過積分得到整個過程的時間,為應(yīng)用動量定理提供了條件.

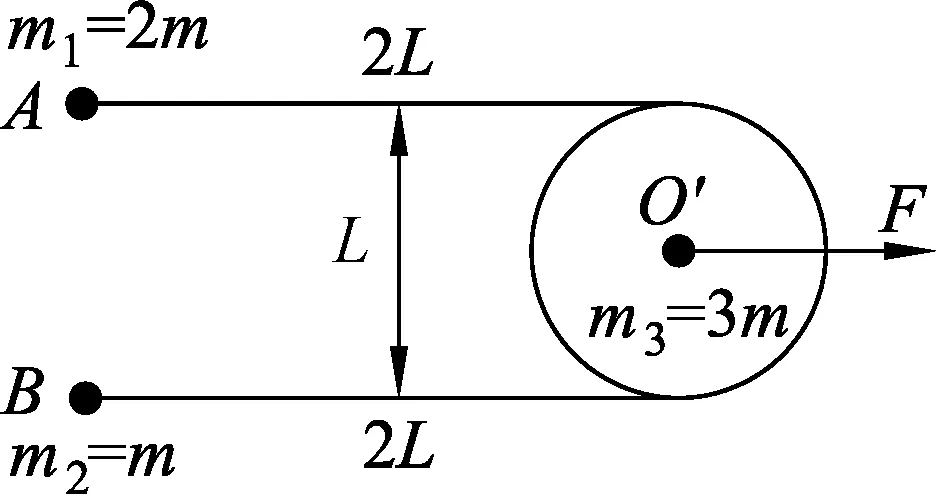
圖6 初始狀態(tài)

例2.如圖6所示,在光滑水平面上放置質(zhì)量分別為m1=2m、m2=m的小球A和B,以及直徑為L、質(zhì)量為m3=3m的平放著的勻質(zhì)圓盤,兩個小球和圓盤邊緣部位用長為2L的兩根平行輕桿固連在一起,組成一個剛體系統(tǒng).開始時系統(tǒng)靜止,在圓盤中心O′處施加一個與輕桿平行的水平恒力F,不計一切摩擦.

(1) 說明此剛體系統(tǒng)將會發(fā)生擺動,并求擺動的最大夾角φ0；

(2) 若考慮φ0較小的情況,試求剛體系統(tǒng)的擺動周期T0.

分析:題目描述的是質(zhì)量分布不均勻的剛體系統(tǒng),外力F的作用線并不通過系統(tǒng)質(zhì)心,若選擇在靜止參考系中完全分析剛體的運動較為困難,不過考慮到剛體系統(tǒng)的質(zhì)心在水平恒力作用下做勻變速直線運動,選擇非慣性質(zhì)心參考系討論該問題不失為一種思路.

解答: (1) 以A和B兩球連線中點為原點,x軸正方向通過圓盤中心水平向右,建立坐標(biāo)系.設(shè)剛體系統(tǒng)質(zhì)心C的位置如圖7所示.由質(zhì)心定義,得系統(tǒng)的質(zhì)心坐標(biāo)為

圖7 質(zhì)心位置

(1)

(2)

在靜止參考系中,對剛體系統(tǒng)應(yīng)用質(zhì)心運動定理,得

(3)

即系統(tǒng)質(zhì)心C沿著水平向右的方向做勻加速直線運動,且始終位于CM直線上.

圖8 圓盤中心O′繞質(zhì)心C擺動

以質(zhì)心C為坐標(biāo)原點,x′坐標(biāo)軸與x坐標(biāo)軸平行,建立隨系統(tǒng)質(zhì)心運動的非慣性質(zhì)心參考系.設(shè)O′C與x′軸的夾角為φ0,以順時針為夾角正方向.如圖8所示.

在質(zhì)心參考系中,外力F作用于圓盤中心O′,相對質(zhì)心C產(chǎn)生力矩,對剛體系統(tǒng)應(yīng)用角動量定理可知,初始時F的力矩為逆時針,使系統(tǒng)繞質(zhì)心C逆時針加速轉(zhuǎn)動,夾角φ0減小,角速度逆時針增加,當(dāng)夾角φ0減為0時,由于角速度不為0圓盤中心將越過x′坐標(biāo)軸,之后F的力矩變?yōu)轫槙r針,使系統(tǒng)逆時針減速轉(zhuǎn)動直至角速度為0.對剛體系統(tǒng)應(yīng)用動能定理,可知在該過程中外力F先做正功后做負(fù)功,其值等大異號,故此時O′C與x′軸的夾角大小仍為φ0.與以上過程類似,之后系統(tǒng)順時針先加速轉(zhuǎn)動再減速轉(zhuǎn)動,直至角速度為0回到圖8狀態(tài).之后再重復(fù)上述過程.

綜上所述,系統(tǒng)將發(fā)生擺動,擺動的最大夾角為

(2) 在質(zhì)心參考系中,設(shè)擺動過程中任意夾角φ,對剛體系統(tǒng)應(yīng)用角動量定理,得

(4)

式中IC為剛體對質(zhì)心的轉(zhuǎn)動慣量.

如圖7所示,質(zhì)心C到上方輕桿、下方輕桿和直線OO′的距離為

(5)

由幾何關(guān)系,得質(zhì)心C到小球A、B和圓盤中心O′的距離為

(6)

由轉(zhuǎn)動慣量定義和平行軸定理,聯(lián)立(6)式,得

(7)

考慮到最大夾角φ0為小角度,故剛體系統(tǒng)的擺動可視為繞質(zhì)心C的簡諧運動,聯(lián)立(4)、(7)式,得簡諧運動方程

(8)

式中圓頻率

擺動周期

點評:靜止參考系中剛體的復(fù)雜運動,在非慣性質(zhì)心參考系中看來卻如此簡單,正是質(zhì)心參考系中質(zhì)心靜止不動這一獨特性質(zhì)的反映.在應(yīng)用角動量定理、動能定理等動力學(xué)規(guī)律時不需要考慮慣性力的影響也源于此.