基于復回歸驗證模式對離心式冷水機故障檢測與診斷技術

曾國安,莊友明

(1.廈門海洋職業技術學院 機電學院,福建 廈門 361000;2.集美大學 機械與能源工程學院,福建 惠安 361000)

0 引 言

離心式冷水機組典型故障分為8類：冷卻水減少、冷凍水減少、制冷劑充注過量、制冷劑泄漏、冷凝器結垢、潤滑油過多、先導閥故障和不凝性氣體.由此引起的冷水機復性能降低和能源消耗，造成無法估計的損失，胡云鵬[1]考慮到冷水機組的復雜性，運用主元分析法(PCA)檢測故障，假設PCA變量具線性關系，制冷系統為高耦合、多工況與多變量系統，其數據具非高斯、非線性特點，導致PCA的檢測效果不理想，且不滿足復雜性.趙云峰[2]將回歸模型用于離心制冷主機的故障診斷，對機組6個參數進行檢測并對機組的運行狀況進行分析，獲得6個參數基準值和計算值間的閾值和殘差，若參數超出相應閾值，則機組被判斷出故障.韓華[3]在平臺實驗上模擬典型的幾種故障和一種并發故障機組共1萬多個樣本和60多個參數，應用互信息(MI-based)和遺傳算法(GA-based)模型選擇出特征故障，然后用PCA提取特征故障，最終選出8個參數作為故障特征參數.用支持向量機(SVM)和智能特征提取兩者結合來診斷單發故障，并以順序集成的SVM與數學解耦標識技術診斷多發故障，對模型試驗以減少20%的故障冷卻水和冷凍水水量所發生的故障，作為人工智能的研究熱點在多個領域受歡迎.不足的是，如易知識組合爆炸即知識獲取出現“瓶頸”問題，知識庫較大時容易使維護困難和推理系統速度慢等.而復回歸驗證模式完成知識庫的組建、網絡推理的過程實際上是網絡的數學計算過程，因此，復回歸驗證模式比其他診斷系統更智能.本研究選用冷水機驗證模式中最具代表性的復回歸驗證模式，探究如何將復回歸驗證模式用于離心式冷水機組的故障診斷，利用冷水機運轉復性能驗證出冷水機組故障檢測率高且適用復回歸模式，以確認冷水機組運行性能，讓冷水機達到最佳的運轉點及最低的耗能.

1 離心式冷水機系統原理

離心式冷水機組系統結構圖如圖1所示.

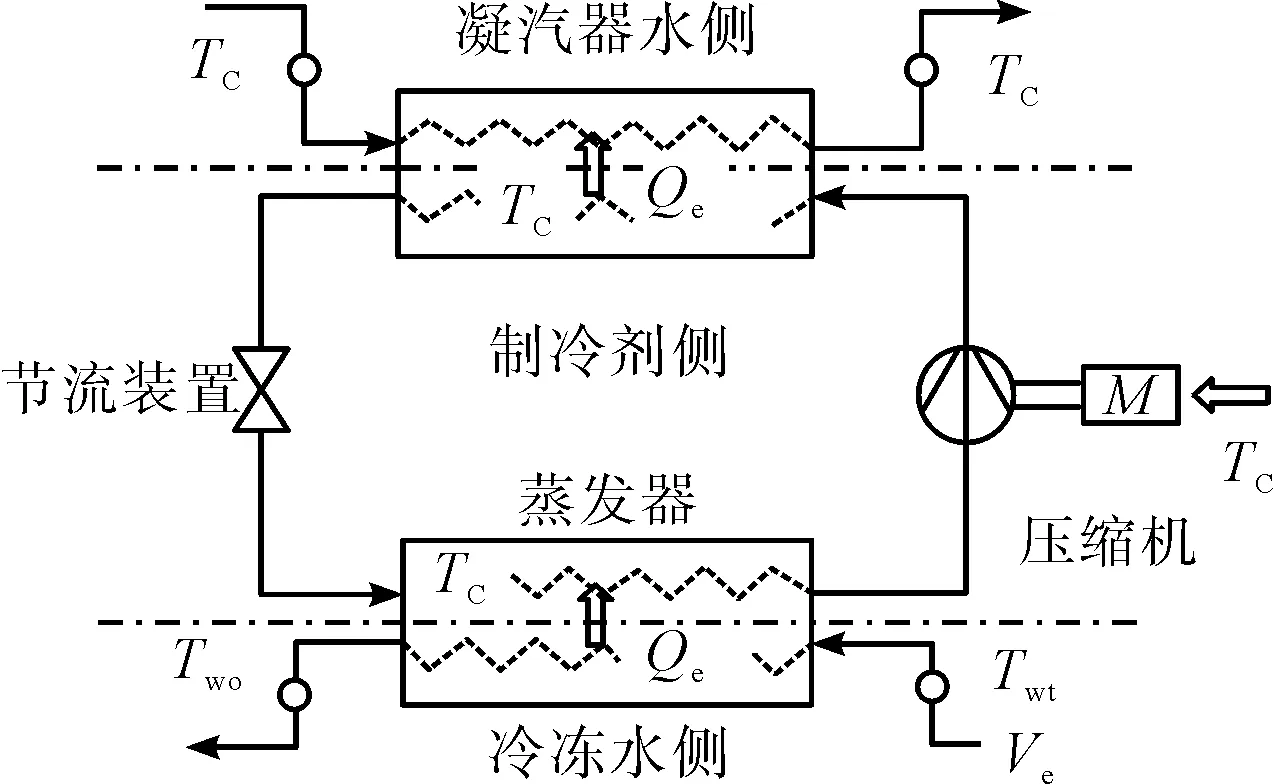
圖1 離心式冷水機系統圖

圖1中為系統運轉時，水側及冷媒側的相關參數，包括蒸發器進出水溫、制冷能力，冷凝器進出水溫、散熱能力及壓縮機的用電量等，各運轉數值的狀況可代表冷水機復性能關系參數.離心式冷水機組的壓縮機制冷壓縮有單級、多級之分，葉輪單級壓力和角速度決定制冷劑分子質量，單級壓縮的壓力比可達3～4，當高溫熱源和低溫熱匯間壓力比超出單級壓縮比時，即可使用分級壓縮、中間冷卻.

2 冷水主機故障檢測與診斷FDD 策略分析

故障檢測基準值是基于可靠操作條件以及信賴區間之下的[4]，利用復性能指標預測基準值與復性能指標實際測量值之間的差異，殘差控制方程如下：

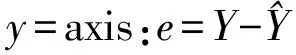
(1)

UCL=CL+3RMSE

(2)

CL=e=0

(3)

LCL=CL-3RMSL

(4)

3 復回歸驗證模式和復回歸分析

將建立冷水主機模式撰寫成程序，通過復性能回歸驗證模式回歸分析，得到一組擁有最佳擬合系數的回歸方程.在故障檢測部分，將監控值代入經過回歸分析得到有最佳擬合系數的回歸方程式，即可得到一組與監控值相同條件下的基準值，判斷此值與監控值的偏差是否超出設定門檻，當此偏差超出設定門檻時，則判斷此系統發生故障.

如影響變量y的因子有x1、x2、x3、x44個獨立變量，故上述因變量與自變量的關系可用數學模型表示，

yi=β0+β1x1+β2x2+…+βkxk+εii=1，2，…，n

(5)

式中，βk為截距，εi為回歸系數.其矩陣表示式為，

(6)

將n個觀察值合并成一矩陣方程式為,

(7)

復回歸模式其回歸方程式的預測誤差越小越好,即殘差越小越好.預測誤差的標準差稱為預測標準誤差(Standard Error of Prediction).從定義上來看,預測標準誤差就是殘差的標準差,也就是殘差值均方的平方根.

在建立各種冷水機復性能回歸驗證模式之后，為了得知模式預測能力的高低，本研究采用下列方程式來評估各項模式中預測能力的精確度與誤差范圍，其方程式如下，

(8)

式中，Yi為第i組預測數據樣本值，Ti為第i組訓練數據樣本值，n為樣本數量.

1)均方根誤差(Root Mean Squared Error，RMSE)為預估預測數據樣本值與實際數據樣本值的誤差大小，誤差越小，代表回歸模式預測越好.

2)變異均方根誤差(coefficient variation of root-mean-square error,CVRMSE),作為估計預測數據樣本值與訓練樣本值之平均誤差百分比，其值越小越好.

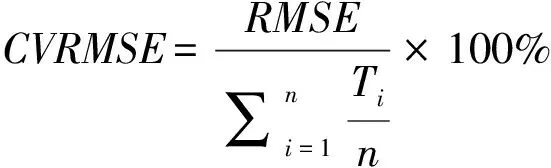
(9)

4 實驗數據分析

4.1 實驗系統與設備

4.1.1 實驗系統

離心式冷水機組故障診斷系統由以下軟件組成：Windows XP作操作系統，用 MATLAB 6.5軟件編制診斷故障程序，用 VisualBasic6.0軟件設計界面.

4.1.2 實驗設備和環境

本研究的節能效果分析主要選用ASHRAE RP-1043 90RT水冷離心式冷水機，其滿負荷制冷量為2 109 kW(600TR)，冷凍水溫為7～12 ℃，冷卻水溫為32～37 ℃，蒸發器污垢系數為0.0176 m2·℃/kW,故障仿真實驗數據，其冷媒使用為 R-134a，冷水機組運轉于27種不同工況和負載條件下，每間隔10 s收集穩態運轉的物理參數[5]，包括冷水入出水溫度、冷卻水入出水溫度、冷水流量、冷卻水流量、蒸發壓力、冷凝壓力、壓縮機出入口溫度、壓縮機出入口過熱度、冷凝器過冷度及壓縮機耗電量，并計算出制冷能力、冷凝能力，詳細分析實驗測量的各項物理量.

4.2 實驗內容

實驗內容除了獲得正常數據外，主要有離心式冷水機運轉過程中最常見的漸變故障數據，其中包括：冷卻水流量減少、冷水流量減少、冷媒泄漏、冷媒充填過多、冷凝器結垢、系統中有不凝結氣體及冷凍油充填過多，具體如圖2所示.

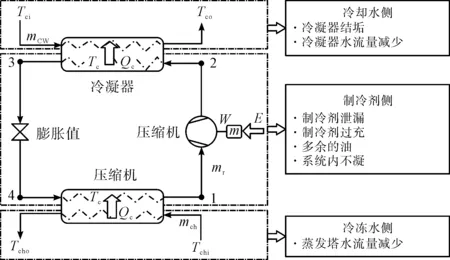
圖2 離心式冷水機運轉中常見漸變故障示意圖

離心式冷水機漸變故障模擬實驗依故障的嚴重程度區分成4個等級，分別為故障等級一(LV1)、故障等級二(LV2)、故障等級三(LV3)及故障等級四(LV4).以下為針對如何設計模擬此離心式冷水機7種漸變故障實驗.

1)冷卻水流量減少(F1).使用電磁閥串聯于冷卻水回路上，改變流過水泵的壓差，使水泵降低流量，以達到模擬冷卻水量減少目的，基準冷卻水量為 818 lpm，并依照不同故障程度，對應1個減少10%的基準水量故障等級.

2)冷水流量減少(F2).使用電磁閥串聯于冷水回路上[6]，改變流過水泵的壓差，使水泵降低流量，以達到模擬冷水量減少的目的，基準冷水量為1 022 lpm，并依照不同故障程度，對應1個減少10%的基準水量故障等級.

3)冷媒泄漏(F3).減少系統中冷媒含量達到仿真冷媒泄漏的目標，基準冷媒量136 kg，并依照不同故障程度，對應1個減少10%的基準冷媒量故障等級.

4)冷媒充填過多(F4).增加系統中冷媒含量達到模擬冷媒充填過多的目的，基準冷媒量為136 kg，并依照不同故障程度，對應1個增加10%的基準冷媒量故障等級.

5)冷凝器結垢(F5).實驗將減少冷凝器內熱交換器的銅管數，達到模擬冷凝器結垢的目的，標準管數為 164 支，并依照不同故障程度，對應1個減少6%的基準冷凝器內管數故障等級.

6)系統中有不凝結氣體(F6).為了消除系統中的不凝結氣體，本實驗將添加氮氣于冷水機中，并依照不同故障程度，氮用氣量為1%～5%.

7)冷凍油充填過多(F7).增加系統中冷凍油含量達到模擬冷凍油充填過多的目的，基準冷凍油量為10 kg，并依照不同故障程度，冷凍油含量為32%～73%.

5 復性能回歸模式預測準確性的評估

復性能回歸驗證模式的適用性分析，針對多種復性能指標，由統計學中預測質量判定準則進行驗證.在此取 F4 LV3 數據對于復性能回歸模式的復性能指標冷凝器趨近溫度(ΔTcapp)及蒸發器對數平均溫度差(Logarithm mean temperaturedifference of evaporator，LMTDe)的圖解為例.利用復性能回歸模式，針對復性能指標ΔTcapp進行預測質量驗證[7]，其所得到的ΔTcapp預測值與訓練值分布情形如圖3所示.

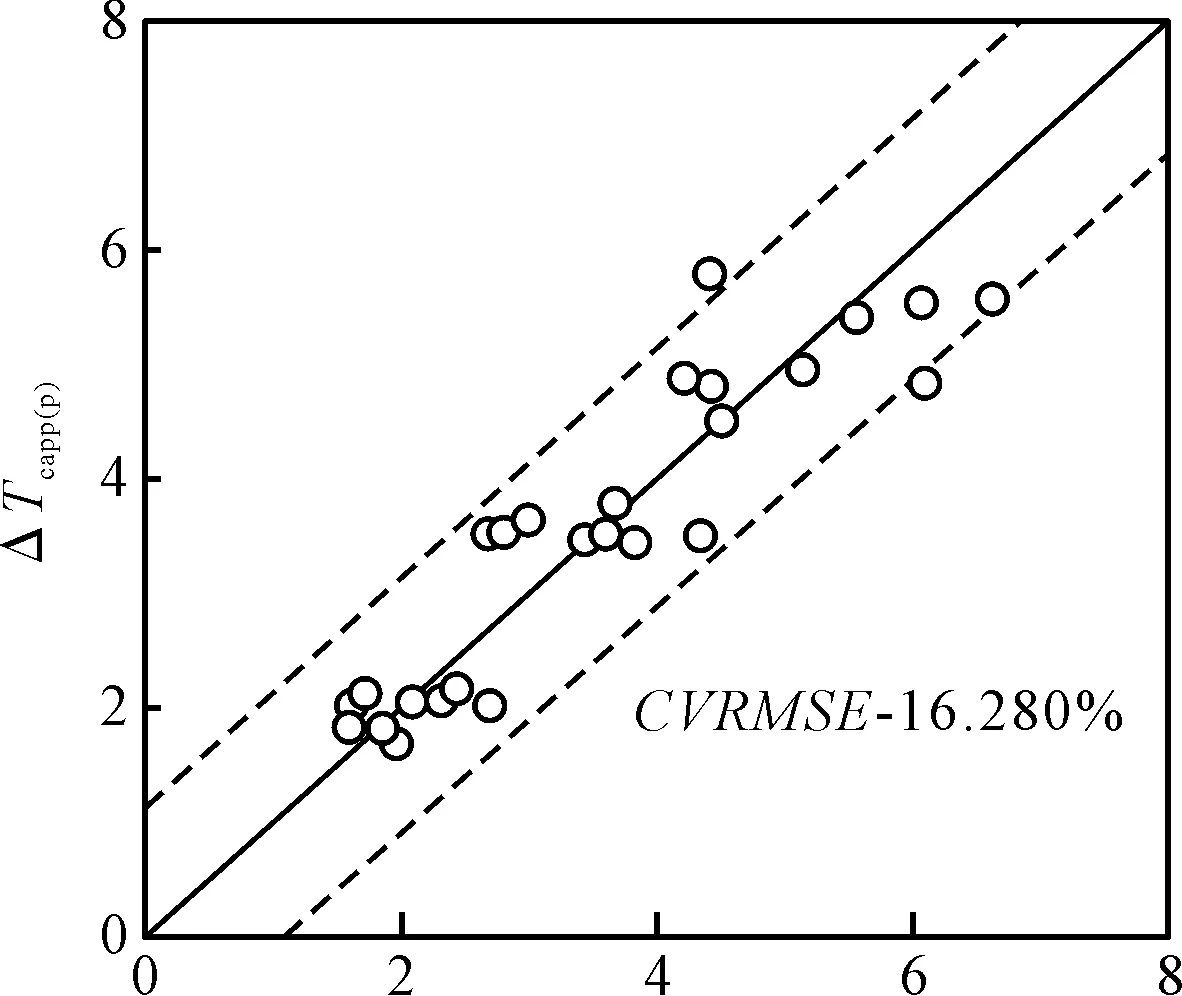
圖3 復回歸于F4 LV3時ΔTcapp 預測值與訓練值分布圖

橫軸為數據經過訓練所得ΔTcapp值，縱軸為使用復性能回歸驗證模式預測所得ΔTcapp值，圖中圓點表示為訓練值與預測值所配置出來的點，當圓點越接近標準配適線(中間黑色實線)時，表示預測質量越好；標準配適線兩端虛線所包圍的區間，即為信賴區間，此區間越窄代表其預測質量越好.由圖3觀察可知，其圓點與標準配適線的偏移程度較小[8]，信賴區間較為狹窄，CVRMSE值較低，為3.992%，故其預測能力較好.

利用復性能回歸模式針對復性能指標LMTDe進行預測質量驗證，其所得到的LMTDe預測值與訓練值分布情形如圖4所示.

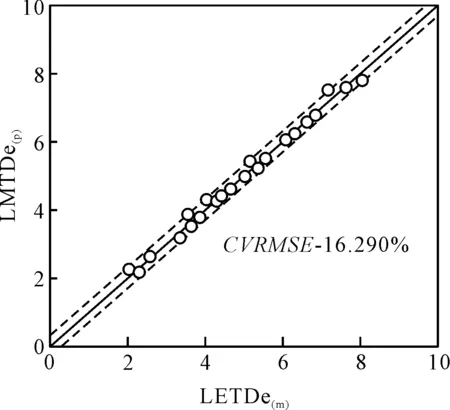
圖4 復回歸于F4 LV3時LMTDe預測值與訓練值分布圖

由圖4可以看出，其圓點與標準配適線的偏移程度比圖3更小，信賴區間更為狹窄，CVRMSE值較低，為2.915%，故其預測能力較好.

由上可知，當預測值與訓練值越接近時，圖中圓點將越接近標準配適線，而信賴區間所包圍的區域越小，且CVRMSE值也相對偏低，表示其復性能回歸驗證模式預測能力越好.由于利用圖解或數值分析皆可獲得相同結果[9]，因此，后面也將以CVRMSE值做為適用性評估的準則，對復性能回歸驗證模式進行數值分析.

離心式冷水機正常運轉數據及故障運轉數據，利用復性能回歸驗證模式進行預測，并用CVRMSE值進行數值分析呈現.綜合分析多種冷水機復性能回歸驗證模式發現，當冷水機在正常運轉時，對于多種復性能指標的預測準確性高，CVRMSE平均值為2.0749%；當冷水機在故障運轉時，復回歸對于多種復性能指標預測準確性仍然較高，CVRMSE平均值為2.0195%.因復回歸所具有的回歸函數為3項，因為此種回歸模式須通過8～10個擬合系數修正，方可呈現較準確的預測能力.綜上所述，發現復性能回歸驗證模式中所具有的回歸函數與擬合系數多少，均可影響準確性預測.回歸模式CVRMSE值為 3～5%以內為可被接受的程度，所使用的復性能回歸驗證模式，對于多種復性能指標平均CVRMSE值皆在5%標準內[10].復回歸對于多種復性能指標的預測準確性較高[11]，CVRMSE總平均值皆為2.03%，故復回歸預測準確性較簡單線性回歸高 72.93%.

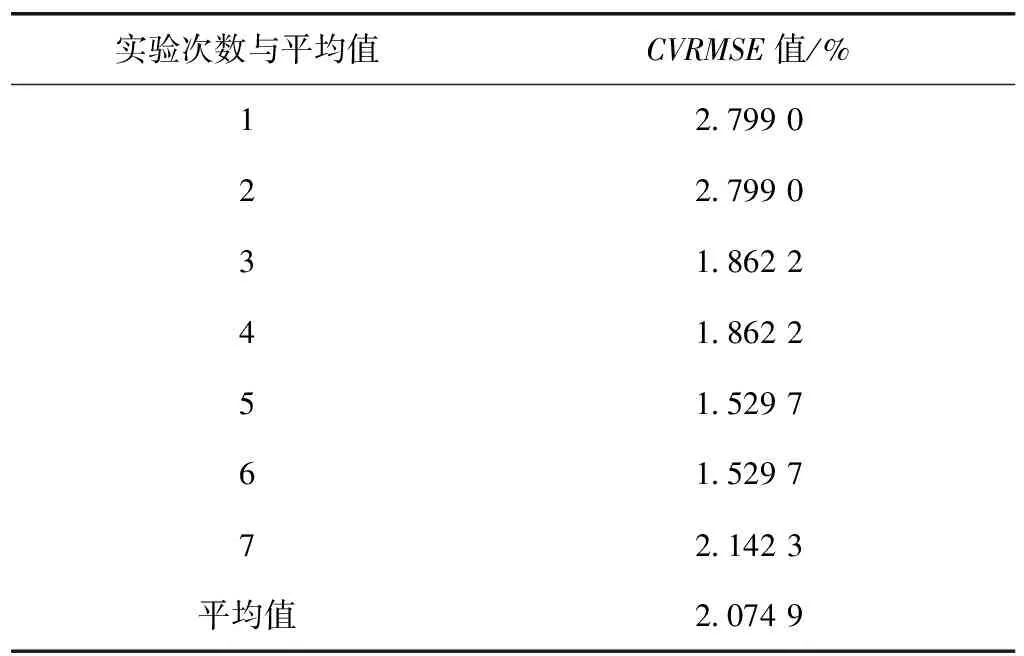
表1 復回歸驗證模式CVRMSE綜合表

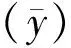
6 結 論

本研究主要探討了離心式冷水機故障檢測與診斷策略中，復回歸驗證模式的預測準確性對于故障檢測率與故障診斷率的影響.復回歸驗證模式，在離心式冷水機故障檢測與診斷率上表現較好，為具有較高預測準確性復性能回歸驗證模式[12].因此，評估結果顯示，復回歸為適用于離心式冷水機故障檢測與診斷策略的復性能回歸驗證模式.將本方法應用于 ASHRAE RP1043 離心式冷水機組[13]進行故障檢測，驗證了該方法的有效性.調速變頻冷水機組可提高節能效率.在對離心式冷水機組變頻改造時，要計算精確、合理科學地確定定頻和變頻離心式冷水機組數量.實際運行時，需依工況不同配置不同運行負荷，最大程度地實現節能效果[14].未來的研究方向可采用深度復回歸學習中的時間序列建模[15]，以保證網絡的泛化能力，使診斷具有較高的經濟價值和節能環保意義.