復雜系統視角下教育-科技-社會協同發展的關系研究

2021-07-11 06:46:14趙志華李茹

中小企業管理與科技·下旬刊 2021年5期

趙志華李茹

【摘? 要】在知識經濟時代，教育、科技和社會的發展是區域經濟發展的主要動力因素，明晰三者之間的協同發展關系是制定區域經濟發展政策措施的基礎。論文建立教育-科技-社會發展復雜系統協同度模型，以浙江等7個省份為例進行實證研究。通過發現三系統協同度的一般規律，為區域發展研究與地方政府政策制定提供理論依據。

【Abstract】In the era of knowledge economy， the development of education， science and technology and society is the main driving force of regional economic development. It is the basis of formulating regional economic development policies and measures to clarify the coordinated development relationship among the three. This paper establishes a coordination degree model of the complex system of education-science and technology-society development， and makes an empirical study of seven provinces including Zhejiang. By finding the general law of the coordination degree of three systems， this paper provides a theoretical basis for regional development research and local government policy-making.

【關鍵詞】區域發展;協同度;面板數據;復雜系統

【Keywords】regional development; coordination degree; panel data; complex system

【中圖分類號】F124;G322? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?【文獻標志碼】A? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?【文章編號】1673-1069（2021）05-0128-02

1 引言

“十四五”時期，為推進區域高質量發展，如何促進各經濟要素間產生“1+1>2”的協同效應成為人們關注的焦點。本文將教育、科技和社會的發展關系放在復合系統的框架下展開研究，分別建立3個子系統的有序度和協同度模型，以浙江等7個省份為研究對象進行實證分析，為各省和地區政府關于區域經濟發展的決策提供參考。

2 研究理論及方法概述

本文設教育、科技和社會系統Si（i=1，2，3），S1代表教育系統;S2代表科技研發系統;S3代表社會系統。假設系統S1的序參量變量為xi=（xi1，xi2，…，xin），？琢ij≤xij≤？茁ij，n≥1，j∈[1，n]，？琢ij和？茁ij分別為系統Si的第j個指標的下限和上限;將指標分為正向指標（xi1，xi2，…，xim）和負向指標（xim+1，xim+2，…，xin），正向指標是指標值越大，有序度越大;同理負向指標是指指標值越小，有序度就越大。而指標的有序貢獻度公式為：

并通過線性加權法，求出系統Si的有序度ui（Xi）：

式（2）中，ωj為第j個指標的權重，并運用熵值法求權重。而系統Si的有序度ui（Xi）∈[0，1]，其值越大，系統Si的有序度就越高，反之則越低。熵值法步驟如下：

①將原始數據歸一化。設m個指標n個對象的原始數據矩陣為：

A=（？琢ij）m×n? ?（3）

將其歸一化得到：

R=（rij）m×n? ?（4）

②定義熵權。第i個指標的熵為：

③定義熵權。第i個指標的熵權：

通過式（1）～（6），計算出各子系統的有序度之后，運用耦合度函數計算兩子系統的協調度：

同時，建立教育、科技創新和社會這三系統協同度模型：

M是Sl、S2和S3三個系統的綜合協同度;而K為調和系數（K≥6）;？漬、？濁和？姿分別是Sl、S2和S3的權重。當U1=U2=U3>0時，三個系統協同發展，達到最佳。

④建立生產函數模型，將7省份中的社會與科技創新，社會與教育以及教育、科技創新和社會三系統協同度作為生產要素（由于后期計算的科技創新與教育協同度發展趨勢未符合模型，因此，科技創新與教育協同度不作為生產要素），分別與固定資產投入和勞動力投入一起建立C—D生產函數：

Y=AK？姿1L？姿2ST？姿3? ? ? ? （9）

Y=BKβ1Lβ2SEβ3? ? ? ? （10）

Y=ZKθ1Lθ2Mθ3? ? ? ? （11）

其中，Y代表GDP;A、B和C代表綜合技術水平;K代表固定資本投入量;L代表年末從業人員數表征;ST代表社會與科技創新的協同度;SE代表社會與教育的協同度;M代表教育、科技創新和社會三系統協同度，而λi、βi和θi（i=1，2，3）分別是在不同協同度下，固定資本、勞動力和協同度對經濟增長的彈性系數。

3 教育、科技創新和社會協同度實證分析

3.1 確定序參量的權重

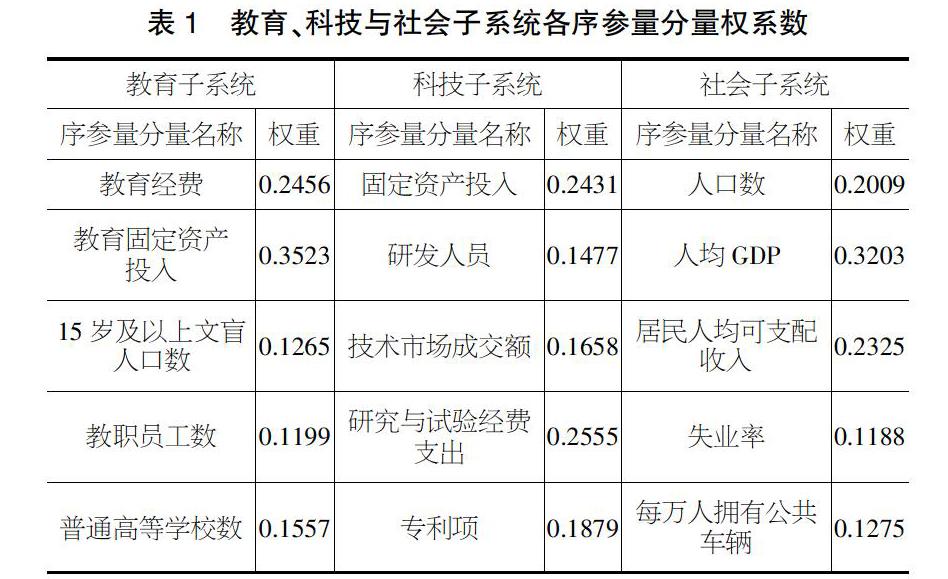
根據公式（3）～（6），計算出7個省份教育、科技創新和社會子系統各序參量分量的權系數，如表1所示。

3.2 協同度計算與模型估計

根據式（1）和式（2），分別計算出2003-2019年間7個省份教育子系統、科技創新子系統和社會發展子系統的有序度。其中，？琢ij、？茁ij分別取2003-2019年三大子系統的序參量分量Xij的最大值的110%和最小值的90%。并運用式（7）和式（8）求得社會與科技子系統的協調度、社會與教育子系統的協調度和教育與科技子系統的協調度以及三大系統之間的協同度。

在此基礎上，利用Eviews8.0軟件對（9）～（11）模型進行估計，結果如下：

（12）

（-2.3301）? ? （18.0071）? （6.1971）

（13）

（-0.0402）? ? （21.0507）? （3.6028）

（14）

（-4.2424）? ? （0.0288）? （0.1599）

（i=1，2，…，7;t=1，2，…，17）

上述回歸模型的擬合優度平均達到了99.5%，擬合效果都較好，而各地區的各協調度的彈性系數λ3i β3i和θ3i的估計結果，如表2所示。

17年來7個省份的教育、科技和社會子系統彼此之間的協同度不斷提升。其中，歷年的教育與科技創新的協同度最大，一直處于高度協同狀態，此外，7個省份的三系統協同度都有不同程度的提高，其中，廣東省綜合協同度最高，內蒙古和四川最低。

4 結論

研究發現：教育與科技創新協同不受地域和時間的影響，教育是科技創新的重要條件，具有使科學轉化為生產技術的中介作用，而科技創新是教育的重要表現，即教育水平越高，科技創新能力越強。因此，為實現教育、科技創新和社會的協同發展，需同時在這三個領域制定相應的政策措施。