帶耗能梁段的高強(qiáng)鋼框筒結(jié)構(gòu)抗震性能試驗(yàn)研究與數(shù)值分析
連鳴 周玉浩 韓文凱
摘 要:為了研究帶可更換剪切型耗能梁段的高強(qiáng)鋼框筒結(jié)構(gòu)(HSS-FTS-RSL)的抗震性能,設(shè)計(jì)了2∶3縮尺子結(jié)構(gòu)試驗(yàn)試件,對(duì)其進(jìn)行低周往復(fù)加載,研究其破壞模式、滯回性能及耗能梁段的可更換能力。基于OpenSees建立了HSS-FTS-RSL結(jié)構(gòu)的簡(jiǎn)化數(shù)值分析模型,數(shù)值分析結(jié)果與試驗(yàn)結(jié)果吻合良好。建立了3種不同耗能梁段布置方式的HSS-FTS-RSL整體結(jié)構(gòu)簡(jiǎn)化數(shù)值模型,對(duì)其進(jìn)行非線性時(shí)程分析。結(jié)果表明:HSS-FTS-RSL子結(jié)構(gòu)試件具有良好的抗震性能,在循環(huán)荷載下表現(xiàn)為耗能梁段的破壞;更換耗能梁段不會(huì)影響結(jié)構(gòu)的抗震性能;結(jié)構(gòu)在地震作用下的變形滿足規(guī)范限制要求;在構(gòu)件截面尺寸相同,即相同用鋼量的前提下,采用高強(qiáng)鋼可以有效降低構(gòu)件的應(yīng)力水平;耗能梁段最大可更換殘余層間側(cè)移角為0.41%,且在大震后整體結(jié)構(gòu)殘余層間側(cè)移角為0.028%~0.148%,可以實(shí)現(xiàn)耗能梁段的更換;基于不同耗能梁段布置方式的HSS-FTS-RSL分析結(jié)果,建議HSS-FTS-RSL結(jié)構(gòu)耗能梁段采用三跨間隔布置。
關(guān)鍵詞:鋼框筒;剪切型耗能梁段;試驗(yàn)研究;抗震性能;簡(jiǎn)化模型
中圖分類號(hào):TU392.5; TU352.1 文獻(xiàn)標(biāo)志碼:A 文章編號(hào):2096-6717(2021)03-0024-13
Abstract: High-strength steel fabricated framed-tube structure with replaceable shear link (HSS-FTS-RSL) was proposed. One 2/3 scaled sub-structure specimen of HSS-FTS-RSL was fabricated. Low cycle reciprocating loading test was carried out for the specimen to study its seismic performance, including failure modes, hysteretic behaviors, and replaceability. The simplified numerical model of HSS-FTS-RSL was established by using OpenSees, and the analysis results of this model had good agreement with the test results. Three simplified numerical models of HSS-FTS-RSL with different layouts of shear links were considered to investigate their seismic performance through the nonlinear dynamic analysis. The results show that the specimen had good seismic performance,
with the failure of energy dissipation beam section under cyclic loading. The maximum interstroy drifts could meet the demands in the seismic code under the ground motions. The high-strength steel could reduce the stress in spandrel beams and columns but not increased the amount of steel of the structures. The maximum residual story drifts ranged from 0.028% to 0.148%, which were lower than the maximum residual story drift of 0.41% for replacing shear links obtained from the test. Considering the seismic performance and repairability of the structure, it was suggested that the shear links of HSS-FTS-RSL should be arranged in three-span interval according to the analysis results.
Keywords: steel framed-tube structure; shear link; experimental study; seismic performance; simplified numerical analysis
鋼框筒結(jié)構(gòu)是由外圍密柱深梁、樓板和內(nèi)部少量柱形成的筒體結(jié)構(gòu),框筒結(jié)構(gòu)具有空間受力性能良好,抗扭及抗側(cè)剛度大等優(yōu)點(diǎn),但由于鋼框筒結(jié)構(gòu)深梁密柱(一般約為3~4 m)的特點(diǎn),導(dǎo)致裙梁的跨高比較小,從而使得裙梁端部彎矩梯度偏大,限制了群梁端部塑性鉸的形成和發(fā)展,不利于結(jié)構(gòu)耗散地震能量;同時(shí),裙梁被樓板加強(qiáng),可能導(dǎo)致地震作用下部分柱子的端部先于裙梁進(jìn)入塑性,加大了結(jié)構(gòu)的倒塌風(fēng)險(xiǎn),損傷嚴(yán)重時(shí),將導(dǎo)致建筑物的功能中斷,產(chǎn)生較高的修復(fù)成本。
近年來(lái),學(xué)者們提出了可恢復(fù)功能抗震結(jié)構(gòu),即地震后不需修復(fù)或者稍加修復(fù)即可恢復(fù)使用功能的結(jié)構(gòu)[1],主要目的是使結(jié)構(gòu)具備震后快速恢復(fù)使用功能的能力,從而減輕由于結(jié)構(gòu)震后功能中斷帶來(lái)的影響。有部分學(xué)者建議在結(jié)構(gòu)中設(shè)置可更換耗能構(gòu)件,以提高結(jié)構(gòu)的震后可恢復(fù)能力。其中,F(xiàn)ortney等[2]最早提出了可更換“保險(xiǎn)絲”,即可更換鋼連梁的概念;Mansour等[3-4]對(duì)腹板螺栓連接剪切型耗能梁段進(jìn)行了滯回性能試驗(yàn),并對(duì)帶端板螺栓連接、雙槽鋼腹板螺栓連接的偏心支撐鋼框架單層單跨結(jié)構(gòu)進(jìn)行了滯回性能試驗(yàn)研究;呂西林等[5]提出了3種不同類型的連梁保險(xiǎn)絲,通過(guò)低周反復(fù)加載試驗(yàn)對(duì)這3種保險(xiǎn)絲的抗震性能進(jìn)行了研究;紀(jì)曉東等[6-7]對(duì)12個(gè)可更換耗能梁段試件進(jìn)行了擬靜力試驗(yàn),研究了其抗震性能及影響參數(shù),其中,剪切型耗能梁段多用于梁跨中,彎曲型耗能梁段多用于梁端部,而剪切型耗能梁段相比于彎曲型耗能梁段有更穩(wěn)定的滯回能力與彈塑性變形能力,從而更好地作為結(jié)構(gòu)中的耗能構(gòu)件進(jìn)行耗能。
針對(duì)傳統(tǒng)鋼框筒結(jié)構(gòu)抗震性能較差且震后修復(fù)比較困難的問(wèn)題,筆者提出了帶可更換剪切型耗能梁段的高強(qiáng)鋼框筒結(jié)構(gòu)(HSS-FTS-RSL),耗能梁段采用屈服強(qiáng)度較低且變形能力較好的鋼材(如Q235鋼),耗能梁段與裙梁間采用傳力明確且易于安裝與拆卸的端板螺栓連接,其余非耗能構(gòu)件(包含裙梁和框筒柱)采用高強(qiáng)度鋼材(如Q460鋼),在大震作用下,耗能梁段完全進(jìn)入彈塑性狀態(tài)進(jìn)行耗能,而其余非耗能構(gòu)件由于采用高強(qiáng)鋼,仍保持彈性或部分發(fā)展塑性,震后僅需更換損傷的耗能梁段即可快速恢復(fù)結(jié)構(gòu)功能。為深入研究HSS-FTS-RSL的抗震性能及震后可更換性,先對(duì)一個(gè)HSS-FTS-RSL子結(jié)構(gòu)進(jìn)行循環(huán)加載試驗(yàn),而后基于試驗(yàn)結(jié)果利用OpenSees建立其簡(jiǎn)化數(shù)值分析模型,并選取3種不同耗能梁段布置方式,建立30層HSS-FTS-RSL整體結(jié)構(gòu)簡(jiǎn)化數(shù)值分析模型,對(duì)其進(jìn)行動(dòng)力彈塑性時(shí)程分析,并對(duì)比不同耗能梁段布置方式對(duì)其抗震性能的影響,基于分析結(jié)果,對(duì)耗能梁段布置方式是否合理提出建議。
1 試驗(yàn)概況
1.1 試驗(yàn)試件
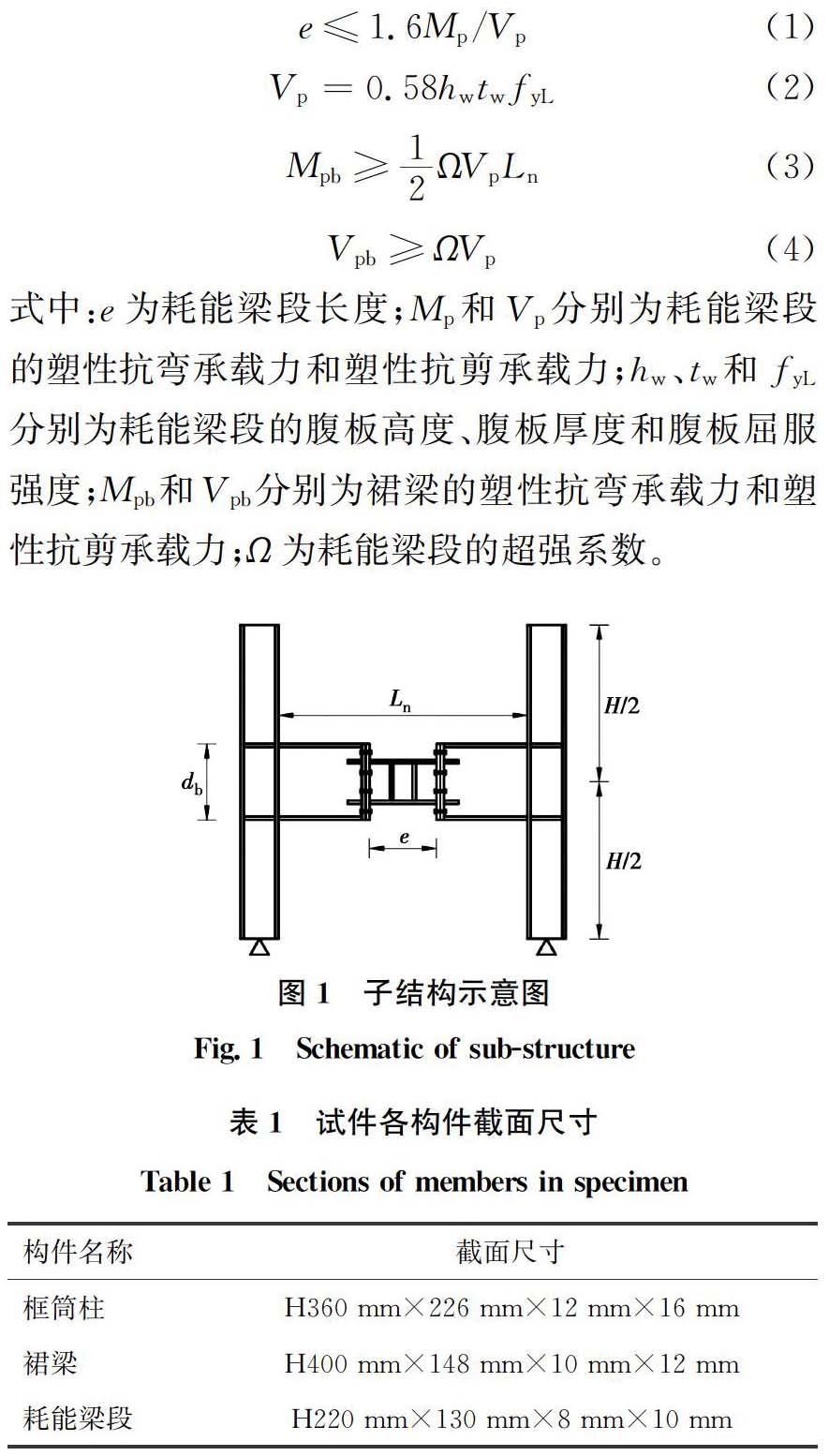
原型結(jié)構(gòu)為一個(gè)30層的HSS-FTS-RSL結(jié)構(gòu),原型結(jié)構(gòu)概況詳見(jiàn)文獻(xiàn)[8]。選取其腹板框架第13層梁柱子結(jié)構(gòu)作為試驗(yàn)原型結(jié)構(gòu),如圖1所示,其中,e、Ln、H分別為耗能梁段長(zhǎng)度、凈跨度和層高。考慮到實(shí)驗(yàn)室的實(shí)際加載條件,最終選取2∶3縮尺試件進(jìn)行試驗(yàn)。根據(jù)式(1)、式(2)設(shè)計(jì)耗能梁段,保證設(shè)計(jì)為剪切屈服型,其中,耗能梁段長(zhǎng)度為400 mm,長(zhǎng)度比e/(Mp/Vp)=1.05。同時(shí),需要保證裙梁端部在耗能梁段充分發(fā)展塑性之前不進(jìn)入塑性,故裙梁截面需滿足式(3)、式(4)。試件各構(gòu)件截面尺寸見(jiàn)表1。
式中:e為耗能梁段長(zhǎng)度;Mp和Vp分別為耗能梁段的塑性抗彎承載力和塑性抗剪承載力;hw、tw和fyL分別為耗能梁段的腹板高度、腹板厚度和腹板屈服強(qiáng)度;Mpb和Vpb分別為裙梁的塑性抗彎承載力和塑性抗剪承載力;Ω為耗能梁段的超強(qiáng)系數(shù)。
耗能梁段與裙梁連接方式采用端板螺栓連接,端板與耗能梁段和裙梁的翼緣均采用全熔透對(duì)接焊縫連接,與耗能梁段和裙梁腹板采用雙面角焊縫連接,焊縫和焊腳尺寸見(jiàn)圖2(b)。高強(qiáng)螺栓承擔(dān)連接處的剪力和彎矩作用,根據(jù)《鋼結(jié)構(gòu)高強(qiáng)度螺栓連接技術(shù)規(guī)程》[9]對(duì)端板螺栓連接的規(guī)定對(duì)連接處螺栓和端板厚度進(jìn)行設(shè)計(jì)。耗能梁段端板和裙梁端板通過(guò)8個(gè)10.9級(jí)M20的摩擦型高強(qiáng)螺栓連接,耗能梁段和端板厚度分別為20、25 mm。裙梁與框筒柱連接處的上下翼緣端部均設(shè)置蓋板,以增強(qiáng)梁柱節(jié)點(diǎn)的轉(zhuǎn)動(dòng)能力及連接強(qiáng)度,試件幾何尺寸與構(gòu)造見(jiàn)圖2。試件中的耗能梁段采用Q235鋼制作,端板采用Q345鋼,框筒柱與裙梁均采用Q460鋼,所用材料的力學(xué)性能數(shù)據(jù)見(jiàn)表2。
1.2 試驗(yàn)裝置與加載方案
試驗(yàn)裝置如圖3所示。框筒柱上下鉸接約束,設(shè)置柱及裙梁側(cè)向支撐防止試件平面外失穩(wěn),側(cè)向支撐與試件接觸面均粘貼1.5 mm厚的四氟乙烯板從而減小側(cè)向支撐與試件之間的摩擦力,通過(guò)壓梁抵抗試驗(yàn)過(guò)程中柱受到的傾覆彎矩,同時(shí),設(shè)置抗剪滑移鍵防止地梁發(fā)生滑移。通過(guò)2個(gè)1 000 kN的同步油壓千斤頂在兩柱柱頂分別施加430 kN的豎向軸力,在加載過(guò)程中保持不變;待豎向荷載N施加穩(wěn)定后,再通過(guò)作動(dòng)器施加水平側(cè)向力P。
水平往復(fù)荷載采用位移控制加載,加載制度如圖4所示,規(guī)定作動(dòng)器推向(向東)為正,拉向(向西)為負(fù)。試驗(yàn)加載分兩個(gè)階段進(jìn)行加載,由于原型結(jié)構(gòu)算例在大震作用下最大層間側(cè)移角為1/80[8],因此,需保證第I階段加載至子結(jié)構(gòu)層間側(cè)移角大于等于1/80后再更換耗能梁段,考察震后耗能梁段的可更換能力。在第I階段,子結(jié)構(gòu)試件屈服前采用3 mm的位移增量進(jìn)行加載,每級(jí)循環(huán)1次,屈服后以0.5Δy′增量進(jìn)行加載,每級(jí)循環(huán)3次,加載至2.5Δy′(層間側(cè)移角為1/80),之后更換耗能梁段;在第Ⅱ階段,對(duì)更換耗能梁段后的試件重新進(jìn)行加載,試件屈服前采用3 mm的位移增量進(jìn)行加載,每級(jí)循環(huán)1次,屈服后以Δy′的倍數(shù)進(jìn)行加載,每級(jí)循環(huán)3次,加載至試件破壞或者承載力下降至峰值的85%,停止加載,試驗(yàn)結(jié)束。其中,Δy′為試驗(yàn)過(guò)程中耗能梁段腹板應(yīng)變片達(dá)到屈服應(yīng)變時(shí)對(duì)應(yīng)的水平加載位移,取18 mm。
1.3 量測(cè)方案
位移測(cè)點(diǎn)及應(yīng)變測(cè)點(diǎn)布置見(jiàn)圖5。為測(cè)量試件水平位移,分別在兩柱柱頂、柱節(jié)點(diǎn)域上部和柱底布置位移傳感器(D3~D8);在耗能梁段處沿耗能梁段兩對(duì)角線方向分別布置兩個(gè)拉線位移計(jì)測(cè)量耗能梁段的剪切變形(D1和D2)。在耗能梁段腹板區(qū)格內(nèi)布置應(yīng)變花,在上下翼緣端部布置應(yīng)變片;在裙梁腹板和翼緣、框筒柱腹板和翼緣布置應(yīng)變片,同時(shí)在梁柱節(jié)點(diǎn)區(qū)域格布置應(yīng)變花;裙梁與柱連接處的上下蓋板處各布置一個(gè)應(yīng)變片。
1.4 試驗(yàn)結(jié)果
在階段I加載過(guò)程中,當(dāng)位移加載至+Δy′第1圈時(shí),耗能梁段腹板屈服,耗能梁段未產(chǎn)生明顯變形。隨著加載位移的增加,腹板處氧化皮逐漸脫落,尤其位于耗能梁段腹板與翼緣連接焊縫周邊較為明顯。2.5Δy′循環(huán)加載完成后,腹板區(qū)格周邊氧化皮明顯脫落,連接區(qū)域及其構(gòu)件均保持彈性狀態(tài)且無(wú)明顯變形。階段I加載結(jié)束后進(jìn)行耗能梁段更換,拆除耗能梁段后連接處未發(fā)現(xiàn)螺栓滑移的痕跡,可以判斷端板螺栓連接傳力可靠且約束作用強(qiáng)。隨后開(kāi)始階段Ⅱ的加載,加載至-4Δy′第3圈時(shí),耗能梁段腹板與加勁肋焊縫端部出現(xiàn)裂紋,見(jiàn)圖6(a);當(dāng)加載至+6Δy′第1圈時(shí),耗能梁段腹板與加勁肋焊縫端部裂紋沿焊縫開(kāi)始延伸,見(jiàn)圖6(b);加載至+6Δy′第2圈時(shí),耗能梁段腹板與加勁肋焊縫附近母材裂縫沿腹板高度方向貫通,腹板區(qū)格斷裂破壞,翼緣發(fā)生屈曲,且加勁肋與下翼緣連接處焊縫斷開(kāi),見(jiàn)圖6(c),試件無(wú)法繼續(xù)承載,試驗(yàn)結(jié)束,試件整體破壞形態(tài)見(jiàn)圖6(d)。
試件階段I與階段Ⅱ的荷載位移曲線如圖7所示。由圖7可知,曲線滯回環(huán)包圍面積隨著加載位移的增大而逐漸增大,并且呈穩(wěn)定、飽滿的梭形,說(shuō)明試件具有穩(wěn)定的耗能能力。此外,兩個(gè)加載階段的荷載曲線變化趨勢(shì)完全一致,相同位移加載級(jí)時(shí)曲線幾乎重合,說(shuō)明更換耗能梁段后試件的抗震性能可以恢復(fù)到初始狀態(tài),達(dá)到了通過(guò)更換耗能梁段即可使結(jié)構(gòu)快速恢復(fù)功能的目的。
1.5 耗能梁段變形
圖8為耗能梁段的剪力塑性轉(zhuǎn)角(V-γp)滯回曲線,圖中的Vn為耗能梁段的名義塑性抗剪承載力,Vp為根據(jù)耗能梁段實(shí)測(cè)強(qiáng)度得到的實(shí)際抗剪承載力。耗能梁段的剪力V和塑性轉(zhuǎn)角γp通過(guò)式(5)~式(7)計(jì)算得到。
式中:H為試件上下鉸接點(diǎn)中心之間的距離;L為試件左右鉸接點(diǎn)中心的距離;Δ1和Δ2分別為交叉位移計(jì)D1和D2量測(cè)的位移值;e為耗能梁段長(zhǎng)度;h為耗能梁段腹板高度,Ks,link為耗能梁段的剪切剛度。
耗能梁段的V-γp滯回曲線飽滿,耗能梁段屈服后表現(xiàn)出了明顯的超強(qiáng)現(xiàn)象,試件的耗能梁段塑性轉(zhuǎn)角遠(yuǎn)大于規(guī)范ANSI/AISC 341-16中規(guī)定的塑性轉(zhuǎn)角限值0.08 rad,說(shuō)明設(shè)置在裙梁中的剪切型耗能梁段具有極強(qiáng)的耗能能力和變形能力。
1.6 耗能梁段的更換
階段I加載結(jié)束后,將水平荷載卸載為零,記錄此時(shí)殘余層間側(cè)移角,為了得到耗能梁段可以更換的最大殘余層間側(cè)移角,利用作動(dòng)器逐步施加水平位移,獲得不需要擴(kuò)孔、切割等操作即可安裝新的耗能梁段所對(duì)應(yīng)的殘余層間側(cè)移角θre,最終得到θre為0.41%。圖9為更換耗能梁段時(shí)的現(xiàn)場(chǎng)照片。
1.7 應(yīng)變分析
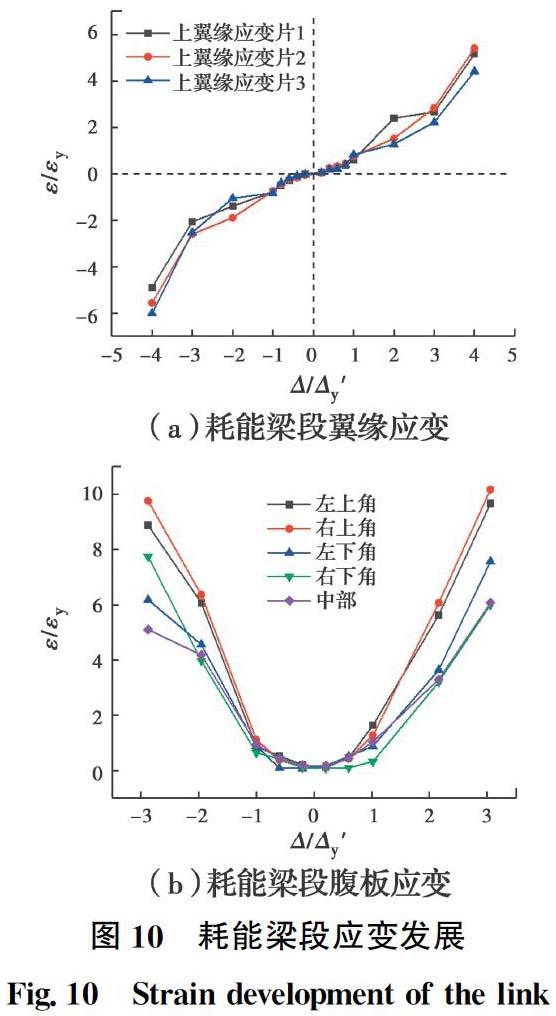
通過(guò)布置在子結(jié)構(gòu)試件各個(gè)位置的電阻應(yīng)變計(jì)采集的數(shù)據(jù),可以分析得到結(jié)構(gòu)各個(gè)部位的內(nèi)力變化,應(yīng)變發(fā)展以及彈塑性發(fā)展?fàn)顟B(tài)。子結(jié)構(gòu)框筒柱腹板和翼緣、裙梁腹板和翼緣、梁柱節(jié)點(diǎn)域以及裙梁上下蓋板耗能梁段腹板和翼緣的應(yīng)變?cè)诩虞d過(guò)程中基于符合平截面假定,始終處于彈性狀態(tài)。圖10給出了耗能梁段腹板和翼緣的應(yīng)變隨加載步的變化規(guī)律,耗能梁段翼緣和腹板截面應(yīng)變?cè)谇半S加載級(jí)增大基本呈線性變化,屈服之后應(yīng)變迅速增大,且翼緣處應(yīng)變發(fā)展速度小于腹板,表明耗能梁段主要通過(guò)腹板剪切屈服進(jìn)入塑性實(shí)現(xiàn)耗能,由于加載級(jí)達(dá)到3Δy′之后腹板塑性發(fā)展嚴(yán)重,表面應(yīng)變花已經(jīng)開(kāi)始脫落,故僅給出3Δy′之前的應(yīng)變數(shù)據(jù)。
2 簡(jiǎn)化數(shù)值模型的建立
2.1 耗能梁段數(shù)值模型
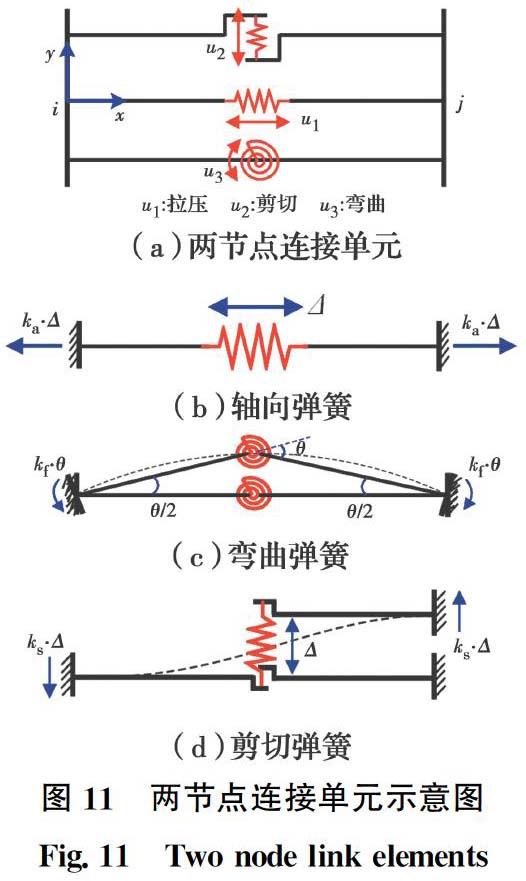
通過(guò)OpenSees中兩節(jié)點(diǎn)連接單元(Two Node Link Element)表征耗能梁段力學(xué)行為。單元在對(duì)應(yīng)自由度上通過(guò)相應(yīng)彈簧表征其力學(xué)行為,將對(duì)應(yīng)材料的本構(gòu)參數(shù)轉(zhuǎn)化為彈簧的恢復(fù)力控制參數(shù)。由于耗能梁段的剪切變形主要為腹板剪切變形,因此,僅考慮耗能梁段腹板平面內(nèi)的力學(xué)行為,忽略腹板平面外及扭轉(zhuǎn)變形的影響。如圖11所示,分別通過(guò)平面內(nèi)的軸向彈簧、彎曲彈簧和剪切彈簧表示。
參考文獻(xiàn)[10]對(duì)混合聯(lián)肢剪力墻中消能連梁的研究,結(jié)構(gòu)中耗能梁段設(shè)計(jì)為剪切屈服型,剪切方向發(fā)生非線性行為,彎曲方向和軸向方向可按彈性考慮。選用OpenSees中的彈性材料表征軸向彈簧及彎曲彈簧恢復(fù)力特性,軸向彈簧及彎曲彈簧的彈性模量分別為耗能梁段的軸向線剛度和彎曲線剛度。文獻(xiàn)[6]的研究結(jié)果表明,剪切型耗能梁段的滯回曲線與鋼材的單軸拉壓滯回曲線特征相近,因此,選用Steel02單軸材料表征剪切彈簧的恢復(fù)力特性,其中Steel02材料參數(shù)通過(guò)單軸拉壓循環(huán)材性試驗(yàn)結(jié)果進(jìn)行標(biāo)定。以往有學(xué)者[11]采用這種模擬方法表征耗能梁段的剪切行為,且取得較好的結(jié)果。彈性材料的本構(gòu)參數(shù)與彈簧恢復(fù)力控制參數(shù)對(duì)應(yīng)關(guān)系見(jiàn)表3,其中E為鋼材彈性模量,A為耗能梁段截面積,I為截面慣性矩,e為耗能梁段長(zhǎng)度。
式中:fy,w為耗能梁段腹板所用鋼材的屈服強(qiáng)度;Aw為腹板截面積;E為鋼材彈性模量;G為鋼材剪切模量;I為截面慣性矩。需要說(shuō)明的是,fy,w、Aw、E、G均取試驗(yàn)子結(jié)構(gòu)耗能梁段的實(shí)測(cè)值。
為得到Steel02中各項(xiàng)參數(shù),需通過(guò)循環(huán)本構(gòu)試驗(yàn)進(jìn)行參數(shù)標(biāo)定。為保證驗(yàn)證準(zhǔn)確性,取試件耗能梁段腹板所用鋼材(Q235-8 mm)進(jìn)行單軸拉壓循環(huán)本構(gòu)試驗(yàn),如圖12所示。采用圖13所示的3種不同的加載制度對(duì)試件進(jìn)行大應(yīng)變循環(huán)加載。基于試驗(yàn)數(shù)據(jù),Steel02參數(shù)標(biāo)定如表4所示,選用單元與耗能梁段保持一致,模擬鋼材循環(huán)加載試驗(yàn),曲線對(duì)比見(jiàn)圖14,由圖14可知,通過(guò)表4中的參數(shù)可較準(zhǔn)確模擬材性試樣在循環(huán)加載作用下的滯回行為。
2.2 裙梁及框筒柱數(shù)值模型
OpenSees中基于力的梁柱單元可以在不細(xì)分單元的情況下較好地模擬構(gòu)件曲率沿長(zhǎng)度非線性分布的情況[12],為考慮其剪切變形,采用OpenSees中截面組裝(Section Aggregator)命令,將截面抗剪剛度賦予基于力的梁柱單元。對(duì)于梁柱單元選用纖維截面,參考杜軻等[12]的研究,為了更好地兼顧精度與計(jì)算效率,對(duì)于基于力的梁柱單元,單根構(gòu)件不需要單元?jiǎng)澐郑瑔卧獌?nèi)使用4個(gè)截面積分點(diǎn),截面上使用6×6的纖維積分點(diǎn)。H型截面劃分如圖15所示。纖維截面劃分采用Steel01材料表征其力學(xué)行為。
2.3 子結(jié)構(gòu)簡(jiǎn)化數(shù)值模型驗(yàn)證
圖16為綜合上述耗能梁段、裙梁和框筒柱所選取的建模方式建立的試驗(yàn)試件簡(jiǎn)化數(shù)值模型,按試驗(yàn)的加載方式對(duì)簡(jiǎn)化數(shù)值模型進(jìn)行分析,模型示意如圖16所示。對(duì)于框筒柱通過(guò)P-delta坐標(biāo)轉(zhuǎn)換命令考慮其P-Δ效應(yīng),加載時(shí)參考上述試驗(yàn)加載制度。
圖17對(duì)比了子結(jié)構(gòu)試驗(yàn)與OpenSees模擬的滯回曲線和骨架曲線。由圖17可知,數(shù)值模擬曲線與試驗(yàn)曲線變化趨勢(shì)基本一致,簡(jiǎn)化模型可以較為準(zhǔn)確地模擬試件的剛度和承載力,且兩者的最大承載力僅相差8.8%。總體上看,基于OpenSees提出的簡(jiǎn)化數(shù)值模型能較好模擬子結(jié)構(gòu)試驗(yàn)試件的滯回行為,且具有較高的精度。
3 結(jié)構(gòu)算例與整體結(jié)構(gòu)簡(jiǎn)化數(shù)值模型
3.1 算例結(jié)構(gòu)
在文獻(xiàn)[8]中30層HSS-FTS-RSL結(jié)構(gòu)的基礎(chǔ)上,設(shè)計(jì)了3個(gè)具有不同耗能梁段布置方式的HSS-FTS-RSL結(jié)構(gòu),分別為三跨間隔布置(HSS-FTS-RSL1)、三跨連續(xù)布置(HSS-FTS-RSL2)以及五跨連續(xù)布置(HSS-FTS-RSL3),設(shè)計(jì)條件為抗震設(shè)防烈度為8度,設(shè)計(jì)地震基本加速度為0.2g,設(shè)計(jì)地震分組為第一組,建筑場(chǎng)地類別為Ⅱ類,場(chǎng)地特征周期為0.35 s。3個(gè)算例結(jié)構(gòu)的立面與平面布置見(jiàn)圖18,構(gòu)件尺寸見(jiàn)表5。需要說(shuō)明的是,在HSS-FTS-RSL結(jié)構(gòu)中,耗能梁段的截面高度小于與其相連的裙梁截面高度(見(jiàn)圖1),因此,樓板不與耗能梁段上翼緣直接連接,故耗能梁段無(wú)需承擔(dān)樓板傳遞的豎向荷載。此外,由于該結(jié)構(gòu)利用耗能梁段的剪切變形進(jìn)行耗能,額外承擔(dān)豎向荷載將不利于其剪切變形的發(fā)展。
3.2 整體結(jié)構(gòu)簡(jiǎn)化模型
采用HSS-FTS-RSL子結(jié)構(gòu)簡(jiǎn)化數(shù)值模型的建模方法,在OpenSees中建立HSS-FTS-RSL整體結(jié)構(gòu)的簡(jiǎn)化數(shù)值模型,其中框筒裙梁、中柱、角柱、內(nèi)柱、內(nèi)梁均采用基于力的梁柱纖維單元,耗能梁段采用兩節(jié)點(diǎn)連接單元。框筒內(nèi)柱及角柱為方鋼管截面,纖維截面劃分示意見(jiàn)圖19。
整體模型采用剛性隔板假定,忽略裙梁軸向變形。模型中的質(zhì)量與豎向荷載分別定義,各層質(zhì)量通過(guò)mass命令集中于各層主節(jié)點(diǎn),作為動(dòng)力分析時(shí)的質(zhì)量源,豎向荷載則取用“1.0倍恒荷載+0.5倍活荷載”均布于框筒裙梁及內(nèi)梁上。整體模型中各材料的屈服強(qiáng)度均采用名義值。
4 算例結(jié)構(gòu)抗震性能分析
4.1 地震波選取
根據(jù)《建筑抗震設(shè)計(jì)規(guī)范》(GB 50011—2010)[13]的要求,從太平洋地震工程中心(PEER)選擇5條天然地震波,同時(shí)用SeismoSiginal軟件根據(jù)場(chǎng)地條件等生成2條人工波,用7條地震波進(jìn)行分析,地震波信息見(jiàn)表5。調(diào)幅后的地震波反應(yīng)譜與抗規(guī)中的反應(yīng)譜對(duì)比見(jiàn)圖20。
4.2 模態(tài)分析
對(duì)算例結(jié)構(gòu)進(jìn)行模態(tài)分析,表6為OpenSees與SAP2000所計(jì)算的3個(gè)算例結(jié)構(gòu)前9階周期對(duì)比,可以看出,采用兩種軟件得到的結(jié)果基本吻合,進(jìn)一步說(shuō)明OpenSees建模有效性。
4.3 屈服機(jī)制
對(duì)各算例結(jié)構(gòu)的簡(jiǎn)化分析模型進(jìn)行單向水平地震作用下的非線性動(dòng)力時(shí)程分析,研究各算例結(jié)構(gòu)在8度小震、中震、大震和超大震下的抗震性能。由于OpenSees中無(wú)法實(shí)現(xiàn)塑性鉸分布結(jié)果可視化,因此,根據(jù)裙梁及框筒柱單元的端部力判斷塑性鉸是否出現(xiàn),判斷準(zhǔn)則參考《鋼結(jié)構(gòu)設(shè)計(jì)標(biāo)準(zhǔn)》(GB 50017—2017)[14],具體見(jiàn)表7。其中,Mce為鉸廣義屈服強(qiáng)度;Mp為構(gòu)件全塑性抗彎承載力;N/Ne為軸壓比;Mx為構(gòu)件端部彎矩。耗能梁段塑性鉸根據(jù)耗能梁段剪力與對(duì)應(yīng)截面屈服剪力進(jìn)行判斷。
圖21為3個(gè)算例結(jié)構(gòu)在RSN9地震波作用下的構(gòu)件塑性鉸分布,由于小震下算例結(jié)構(gòu)各構(gòu)件均處于彈性狀態(tài),因此,僅給出中震、大震和超大震下的結(jié)構(gòu)塑性鉸分布。由圖21可知:中震時(shí),各算例結(jié)構(gòu)的部分耗能梁段達(dá)到屈服,其余構(gòu)件均保持彈性;大震時(shí),HSS-FTS-RSL1除頂層中跨耗能梁段外,其余耗能梁段均進(jìn)入塑性,個(gè)別邊跨裙梁端部出現(xiàn)塑性鉸,HSS-FTS-RSL2耗能梁段同樣進(jìn)入塑性,且邊部三跨裙梁出現(xiàn)塑性鉸且數(shù)量較多,HSS-FTS-RSL3頂部個(gè)別耗能梁段還未進(jìn)入塑性,個(gè)別邊跨裙梁端部出現(xiàn)塑性鉸;超大震時(shí),HSS-FTS-RSL1與HSS-FTS-RSL3的中下部樓層裙梁出現(xiàn)較多塑性鉸,但柱端均未出現(xiàn)塑性鉸,而HSS-FTS-RSL2的裙梁出現(xiàn)塑性鉸較其他算例結(jié)構(gòu)更多,且底部樓層中柱柱端出現(xiàn)塑性鉸。由此可見(jiàn),在水平地震作用下,HSS-FTS-RSL的耗能梁段首先屈服形成塑性鉸,隨著地震作用增強(qiáng),裙梁進(jìn)入塑性形成塑性鉸。HSS-FTS-RSL2不僅裙梁出現(xiàn)塑性鉸較多,且底層個(gè)別柱端也形成塑性鉸,增加了結(jié)構(gòu)的倒塌風(fēng)險(xiǎn),HSS-FTS-RSL1與HSS-FTS-RSL3僅在裙梁處進(jìn)入塑性,因此,HSS-FTS-RSL1與HSS-FTS-RSL3的屈服機(jī)制更理想。
4.4 基底剪力與角柱應(yīng)力
表8給出了各算例結(jié)構(gòu)在不同水準(zhǔn)地震作用下的基底剪力。由表8可知:在小震時(shí),3個(gè)算例結(jié)構(gòu)的基底剪力標(biāo)準(zhǔn)差約為均值的14%,而在中震、大震、超大震時(shí)約為10%,表明隨著地震作用增強(qiáng),結(jié)構(gòu)進(jìn)入彈塑性后,基底剪力的離散性會(huì)有一定程度減小;HSS-FTS-RSL1與HSS-FTS-RSL2的基底剪力相差不大,說(shuō)明在耗能梁段數(shù)量相同的情況下改變布置方式對(duì)結(jié)構(gòu)基底剪力響應(yīng)沒(méi)有明顯影響;HSS-FTS-RSL3的基底剪力與HSS-FTS-RSL1最大相差10%,與HSS-FTS-RSL2最大相差14%,說(shuō)明當(dāng)耗能梁段數(shù)量增多時(shí),由于塑性內(nèi)力重分布,降低了結(jié)構(gòu)的基底剪力。
由于HSS-FTS-RSL中梁、柱構(gòu)件采用Q460鋼以期降低非耗能構(gòu)件的應(yīng)力水平,因此,提取結(jié)構(gòu)受力相對(duì)較大的底層角柱應(yīng)力時(shí)程曲線予以說(shuō)明。分別提取底層4個(gè)角柱受力最大的4個(gè)角部纖維點(diǎn)的應(yīng)力時(shí)程,選擇對(duì)應(yīng)應(yīng)力峰值最大纖維點(diǎn)的應(yīng)力時(shí)程曲線,見(jiàn)圖22。由圖22可知:大震及超大震時(shí),個(gè)別地震波作用下底層角柱的應(yīng)力峰值趨于460 MPa,但總體保持在345~460 MPa之間。說(shuō)明在構(gòu)件截面尺寸相同即不增加結(jié)構(gòu)用鋼量的前提下,由于高強(qiáng)鋼強(qiáng)度高,可以明顯提升構(gòu)件的屈服承載力,相對(duì)于Q345鋼材,可以有效降低構(gòu)件的應(yīng)力水平,使非耗能構(gòu)件在大震作用下處于彈性,降低結(jié)構(gòu)主體的損傷,有利于結(jié)構(gòu)震后修復(fù)。
4.5 層間側(cè)移角
圖23給出了3個(gè)算例結(jié)構(gòu)在不同水準(zhǔn)地震作用下層間側(cè)移角平均值的對(duì)比。由圖23可知:各算例結(jié)構(gòu)的彈性和彈塑性最大層間側(cè)移角均能滿足《建筑抗震設(shè)計(jì)規(guī)范》的限值要求;在小震時(shí),結(jié)構(gòu)整體保持彈性,此時(shí)改變耗能梁段數(shù)量及布置方式對(duì)結(jié)構(gòu)層間側(cè)移角分布沒(méi)有影響;中震時(shí),3個(gè)算例結(jié)構(gòu)耗能梁段開(kāi)始屈服,HSS-FTS-RSL2層間側(cè)移角相對(duì)較大,其最大層間側(cè)移角比HSS-FTS-RSL1和HSS-FTS-RSL3分別高3.3%和4.9%;大震時(shí),HSS-FTS-RSL2層間側(cè)移角最大,分別比HSS-FTS-RSL1和HSS-FTS-RSL3的高6.9%和12.7%;超大震時(shí),HSS-FTS-RSL2最大層間側(cè)移角比HSS-FTS-RSL1和HSS-FTS-RSL3分別高4.4%和13.8%。因此,當(dāng)耗能梁段屈服后,結(jié)構(gòu)耗能梁段布置越多,可以有效降低結(jié)構(gòu)的層間側(cè)移角,避免結(jié)構(gòu)出現(xiàn)明顯薄弱層,在耗能梁段布置數(shù)量一定時(shí),相比于每跨連續(xù)布置,采用間隔跨布置可以在一定程度上降低結(jié)構(gòu)層間側(cè)移角。
4.6 殘余層間側(cè)移角
圖24為各算例結(jié)構(gòu)殘余層間側(cè)移角平均值對(duì)比,其中殘余層間側(cè)移角取地震動(dòng)輸入結(jié)束后經(jīng)過(guò)10 s的自由振動(dòng),頂點(diǎn)速度基本衰減為零的層間側(cè)移[9]。在中震時(shí),3個(gè)算例結(jié)構(gòu)殘余層間側(cè)移角沿高度分布相對(duì)均勻且基本一致,這是由于中震時(shí)僅有部分樓層耗能梁段屈服,且進(jìn)入塑性程度相對(duì)較小,因此,3個(gè)算例結(jié)構(gòu)殘余變形差別不大;大震時(shí),由于HSS-FTS-RSL3采用五跨連續(xù)布置,耗能梁段個(gè)數(shù)相對(duì)較多且耗能梁段進(jìn)入塑性程度增加,因此,殘余變形比另外兩算例結(jié)構(gòu)更大,但是各算例結(jié)構(gòu)的最大殘余層間側(cè)移角介于0.028%~0.148%;超大震時(shí),由于裙梁端部出現(xiàn)塑性鉸,且HSS-FTS-RSL2中下部樓層個(gè)別柱端也出現(xiàn)塑性鉸,更大程度降低了結(jié)構(gòu)整體剛度,導(dǎo)致HSS-FTS-RSL2在超大震時(shí)殘余變形最大。因此,增加耗能梁段布置數(shù)量會(huì)在一定程度上增大結(jié)構(gòu)震后殘余變形。此外,3個(gè)算例結(jié)構(gòu)殘余層間側(cè)移角均遠(yuǎn)小于試驗(yàn)所得的耗能梁段可更換對(duì)應(yīng)的結(jié)構(gòu)最大殘余層間側(cè)移角0.41%,因此,HSS-FTS-RSL結(jié)構(gòu)在大震后可以實(shí)現(xiàn)耗能梁段的更換,從而快速恢復(fù)結(jié)構(gòu)的使用功能,而超大震時(shí)雖然結(jié)構(gòu)部分裙梁及框筒柱出現(xiàn)塑性鉸,但結(jié)構(gòu)并沒(méi)有倒塌風(fēng)險(xiǎn)。因此,HSS-FTS-RSL結(jié)構(gòu)能夠達(dá)到“小震不壞,中震大震可更換修復(fù),超大震不倒塌”的抗震設(shè)防目標(biāo)。
5 結(jié)論
對(duì)HSS-FTS-RSL子結(jié)構(gòu)試件進(jìn)行了低周往復(fù)加載試驗(yàn),基于試驗(yàn)結(jié)果與OpenSees平臺(tái)建立了HSS-FTS-RSL結(jié)構(gòu)的簡(jiǎn)化數(shù)值模型,在此基礎(chǔ)上建立了具有3種不同耗能梁段布置方式的HSS-FTS-RSL結(jié)構(gòu)簡(jiǎn)化數(shù)值分析模型,通過(guò)非線性動(dòng)力時(shí)程分析研究了HSS-FTS-RSL結(jié)構(gòu)的抗震性能,比較了耗能梁段數(shù)量及布置方式對(duì)結(jié)構(gòu)抗震性能的影響,并提出了相關(guān)建議。
1)HSS-FTS-RSL子結(jié)構(gòu)試件在低周往復(fù)荷載下具有穩(wěn)定的承載力、剛度及良好的耗能能力,破壞集中于耗能梁段,其余非耗能構(gòu)件處于彈性狀態(tài),利于震后修復(fù),耗能梁段與裙梁間采用端板螺栓連接,該連接方式傳力可靠,沒(méi)有出現(xiàn)螺栓滑移。
2)基于OpenSees建立HSS-FTS-RSL結(jié)構(gòu)的簡(jiǎn)化數(shù)值分析模型,其中耗能梁段采用兩節(jié)點(diǎn)連接單元建立,裙梁、內(nèi)梁、框筒柱及內(nèi)柱均采用基于力的纖維梁柱單元建立,該模型具有較高模擬精度,可用于整體結(jié)構(gòu)分析。
3)不同耗能梁段布置方式對(duì)結(jié)構(gòu)的抗震性能影響顯著,但結(jié)構(gòu)在地震作用下的變形滿足規(guī)范限制要求。當(dāng)耗能梁段數(shù)量增多時(shí),可有效降低結(jié)構(gòu)基底剪力與層間側(cè)移角,并且在耗能梁段布置數(shù)量相同時(shí),相比于連續(xù)布置,采用間隔布置可以在一定程度上降低結(jié)構(gòu)層間側(cè)移角。
4)HSS-FTS-RSL結(jié)構(gòu)在大震下的殘余層間側(cè)移角均小于由試驗(yàn)確定的耗能梁段可更換殘余層間側(cè)移角0.41%,表明該結(jié)構(gòu)在大震后可以實(shí)現(xiàn)耗能梁段的更換,從而快速恢復(fù)結(jié)構(gòu)的使用功能,而超大震時(shí)雖然部分裙梁及框筒柱出現(xiàn)塑性鉸,但結(jié)構(gòu)并沒(méi)有倒塌風(fēng)險(xiǎn)。說(shuō)明HSS-FTS-RSL結(jié)構(gòu)能夠達(dá)到“小震不壞,中震大震可更換,超大震不倒塌”的抗震設(shè)防目標(biāo)。
5)綜合考慮結(jié)構(gòu)的基底剪力、最大層間側(cè)移角、殘余層間側(cè)移角等抗震性能指標(biāo),耗能梁段采用三跨間隔布置及五跨連續(xù)布置方式均可,但考慮到耗能梁段布置數(shù)量較多會(huì)導(dǎo)致震后修復(fù)成本增大,建議HSS-FTS-RSL結(jié)構(gòu)的耗能梁段采用三跨間隔布置。
參考文獻(xiàn):
[1] 呂西林, 陳云, 毛苑君. 結(jié)構(gòu)抗震設(shè)計(jì)的新概念: 可恢復(fù)功能結(jié)構(gòu)[J]. 同濟(jì)大學(xué)學(xué)報(bào)(自然科學(xué)版), 2011,39(7): 941-948.
LU X L, CHEN Y, MAO Y J. New concept of structural seismic design: earthquake resilient structures [J]. Journal of Tongji University (Natural Science), 2011,39(7): 941-948. (in Chinese)
[2] FORTNEY P J, SHAHROOZ B M, RASSATI G A. Large-scale testing of a replaceable “fuse” steel coupling beam [J]. Journal of Structural Engineering, 2007, 133(12): 1801-1807.
[3] MANSOUR N, CHRISTOPOULOS C, TREMBLAY R. Seismic design of EBF steel frames using replaceable nonlinear links [C]//Proceedings of 2006 STESSA conference, Yokohama, Japan, 2006: 745-750.
[4] MANSOUR N, CHRISTOPOULOS C, TREMBLAY R. Experimental validation of replaceable shear links for eccentrically braced steel frames [J]. Journal of Structural Engineering, 2011, 137(10): 1141-1152.
[5] 呂西林, 陳云, 蔣歡軍. 可更換連梁保險(xiǎn)絲抗震性能試驗(yàn)研究[J]. 同濟(jì)大學(xué)學(xué)報(bào)(自然科學(xué)版), 2013,41(9): 1318-1325,1332.
LU X L, CHEN Y, JIANG H J. Experimental study on seismic behavior of “fuse” of replaceable coupling beam [J]. Journal of Tongji University (Natural Science),2013,41(9): 1318-1325,1332. (in Chinese)
[6] 紀(jì)曉東, 馬琦峰, 王彥棟, 等. 鋼連梁可更換消能梁段抗震性能試驗(yàn)研究[J]. 建筑結(jié)構(gòu)學(xué)報(bào), 2014,35(6): 1-11.
JI X D, MA Q F, WANG Y D, et al.Cyclic tests of replaceable shear links in steel coupling beams [J]. Journal of Building Structures, 2014,35(6): 1-11. (in Chinese)
[7] 紀(jì)曉東, 王彥棟, 馬琦峰, 等. 可更換鋼連梁抗震性能試驗(yàn)研究[J]. 建筑結(jié)構(gòu)學(xué)報(bào), 2015,36(10): 1-10.
JI X D, WANG Y D, MA Q F, et al.Experimental study on seismic behavior of replaceable steel coupling beams [J]. Journal of Building Structures, 2015,36(10): 1-10. (in Chinese)
[8] 連鳴, 韓文凱, 莫文茹, 等. 可更換剪切型耗能梁段-高強(qiáng)鋼框筒結(jié)構(gòu)抗震性能分析[J]. 建筑結(jié)構(gòu), 2020,50(1): 74-82.
LIAN M, HAN W K, MO W R, et al.Investigation on seismic performance of high-strength steel fabricated steel framed-tube structure with replaceable shear type energy-dissipated beam section [J]. Building Structure, 2020,50(1): 74-82. (in Chinese)
[9] 鋼結(jié)構(gòu)高強(qiáng)度螺栓連接技術(shù)規(guī)程: JGJ 82—2011 [S]. 北京: 中國(guó)建筑工業(yè)出版社, 2011.
Technical specification for high strength bolt connections of steel structures: JGJ 82-2011 [S]. Beijing: China Architecture & Building Press, 2011. (in Chinese)
[10] 孫亞. 帶可更換鋼連梁的混合聯(lián)肢剪力墻抗震性能研究[D]. 北京: 清華大學(xué), 2015.
SUN Y. Study on seismic behavior of hybrid coupled wall with replaceable steel coupling beams [D]. Beijing: Tsinghua University, 2015. (in Chinese)
[11] JI X D, LIU D, MOLINA HUTT C. Seismic performance evaluation of a high-rise building with novel hybrid coupled walls [J]. Engineering Structures, 2018, 169: 216-225.
[12] 杜軻, 孫景江, 許衛(wèi)曉. 纖維模型中單元、截面及纖維劃分問(wèn)題研究[J]. 地震工程與工程振動(dòng), 2012,32(5): 39-46.
DU K, SUN J J, XU W X. The division of element, section and fiber in fiber model [J]. Journal of Earthquake Engineering and Engineering Vibration, 2012,32(5): 39-46. (in Chinese)
[13] 建筑抗震設(shè)計(jì)規(guī)范: GB 50011—2010 [S]. 北京: 中國(guó)建筑工業(yè)出版社, 2010.
Code for seismic design of buildings: GB 50011-2010 [S]. Beijing: China Architecture & Building Press, 2010. (in Chinese)
[14] 鋼結(jié)構(gòu)設(shè)計(jì)標(biāo)準(zhǔn): GB 50017—2017 [S]. 北京: 中國(guó)建筑工業(yè)出版社, 2017.
Standard for design of steel structures: GB 50017-2017 [S]. Beijing: China Architecture & Building Press, 2017. (in Chinese)
(編輯 胡玲)

