三坐標測量機接觸模型構建及數值算法研究

薛 秦，朱僖禧

(中國礦業大學徐海學院 信息與電氣工程系 ，江蘇 徐州 221008)

0 引言

在精密制造領域中，球類零件的應用日趨廣泛，對球面的精度要求也越來越嚴格。球面的形狀誤差，其精度高低對球類零件的質量、工作性能和使用壽命有很重要的影響。在精密測試領域，計算機輔助測試技術不僅能完成尺寸、曲線、曲面的精密測量，還能進行形位誤差的精確評定[1-3]。微納米坐標測量機(CMMs)作為一種測量儀器，它的出現標志著計量儀器從傳統的手動測量向現代化的自動測試技術過渡的一個里程碑。通過對三坐標測量機探頭球面中心的坐標測量，將其轉換為被測表面各點的坐標。這個過程通常稱為測量探頭半徑的補償[4-6]。在實際測量中，曲面在形狀和位置上的偏差量總是與計算機輔助設計測量模型不同。對于探測球頭上的點的坐標，它是在一定誤差下確定的[7-8]。復雜曲面確定點的坐標與被測表面的曲率以及探頭球體的半徑有關，被測表面曲率和探頭球體的半徑越大，確定表面點的坐標時產生的誤差就越大[9-11]。

在實際測量軸承、凸輪、機床、機身和渦輪葉片等零件的復雜表面時，通常需要在探測球頭球體形狀等方面考慮以提高其精度[12]。針對目前CMM在復雜曲面測量中缺乏一個完整的數學體系，提出了一種新的球頭與零件表面接觸點的數學模型和數值算法。即使在球面上使用了大量的點，也具有良好的收斂性。實驗在測量圓環形標稱表面的滾珠軸承內圈與凸輪輪廓時，成功地測試了球形探針半徑補償形狀誤差的方法，并且得到實際的凸輪輪廓線。

1 復雜曲面與球體半徑補償

以前能夠實現三維補償確定曲面法向經常用的是微平面法。為了確定被測曲面的法向，如圖1所示，可以在Q點附近測若干個點，例如測Q1、Q2、Q3，三個點(也可以取多個點)，然后通過Q1、Q2、Q3三點作一個平面，這一微小平面的法線即近似為曲面的法線。為了確定Q點的法線方向，通常采用方形網格，如圖2所示。但不是簡單地在Q點附近再去測4個點，而是利用與它相鄰近的4個網格點Q1、Q2、Q3、Q4，然后用最小二乘法確定它的最佳擬合平面及其法線方向。值得注意的是，在實際測量中，直接得到的并不是測量點Q與Q1、Q2、Q3、Q4的坐標，而是測量Q點和Qi點時測端球心位置Q及Qi的坐標，必須根據這些擬合平面的法向進行測頭半徑補償，才能得到Q和Qi各點坐標值。

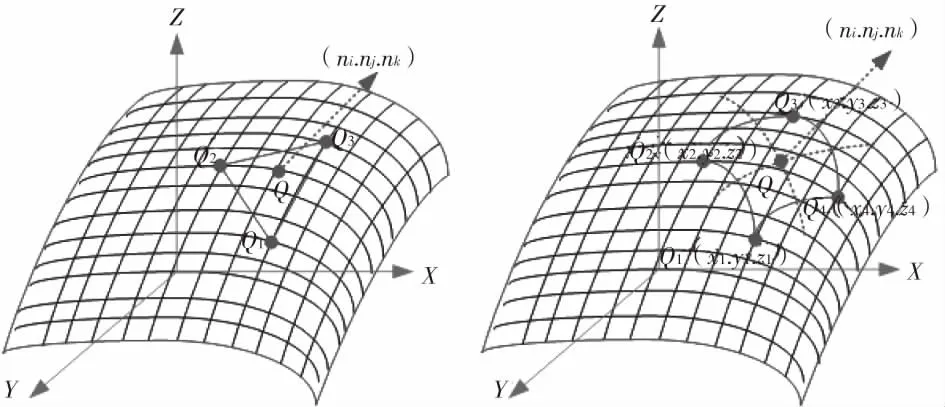
圖1 微平面法三維補償 圖2 微平面法求曲面法向

在計算復雜曲面與球體之間的接觸點坐標時，通常因為名義曲面和實際曲面兩者的法線不一致而產生誤差。這跟曲面的形狀和控制點的錯誤排列有很大的關系，而這些因素在現階段無法確定。因此，現在的很多研究人員傾向于借助于各種算法來優化法線的位置，從而使誤差最小化。接觸點坐標的準確度與探頭球體的形狀和尺寸密切相關。大量的測量實驗表明球內誤差占總測量誤差的10.4%以上，這對于復雜曲面的相關研究工作及其不利[13-14]。因此針對探測球頭形狀偏差，本文提出了一種新的方法來測量復雜曲面。在該方法中，對測得球面上的點進行雙三角多項式逼近并建立其三維模型。圖3則為半徑補償的測頭和零件的理想接觸示意圖。

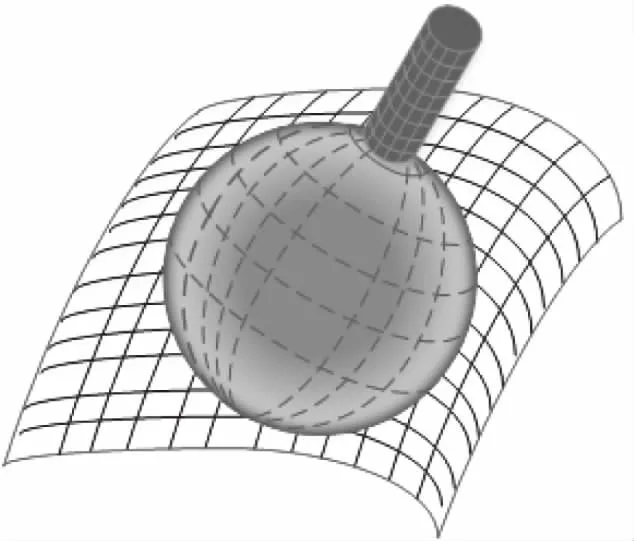
圖3 測頭和零件的理想表面

本文提出的方法主要針對探測球頭的形狀偏差，需要建立一個新的數學模型。算法使用球體表面任何點的法線通過其中心。因此，復雜曲面與探測球體接觸點的計算是通過一種數值算法來實現。利用球面上的點在法向上與標稱表面的距離最小。因此探測球體面向被測表面部分上的所有點形成一個循環，然后在與法向相交的條件下，在名義面上均有一個對應點；最后從找到的所有距離值中選擇一個最小距離，根據最小距離值δi，可以認為球體與復雜曲面的接觸點位置即對應于找到的最小距離的方向。

2 三坐標測量曲面模型構建

使用三個笛卡爾坐標系(圖4)進行坐標測量。其中包括：(1)坐標測量機固定系統(X0，Y0，O0，Z0)；(2)固定件系統(X1，Y1，O1，Z1)；(3)移動探針系統(X2，Y2，O2，Z2)。一般情況對于三個坐標系而言，它們的相互位置是已知的。通過使用CMM軟件來完成一個坐標系到另一個坐標系的轉換。

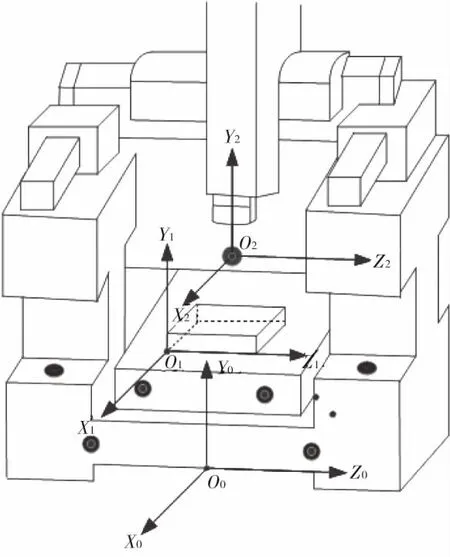
圖4 CMM測量坐標系模型

計算的初始數據：1)坐標x1、y1、z1和法線方向n1X、n1Y、n1Z的零件標稱表面；2)中心坐標為x20，y20，z20和表面坐標為x2i，y2i，z2i的球體。

接觸點處標稱表面的法向參數方程為：

(1)

其中t是標準參數。

球體的參數方程可以表示為：

(2)

其中，θ，φ是球體在經緯度上的角度；ri是球體上第i個點的半徑。具體示意圖如圖5所示。球面點的半徑ri可以以數組的形式給出(θ，φ，ri)或通過依賴關系近似：

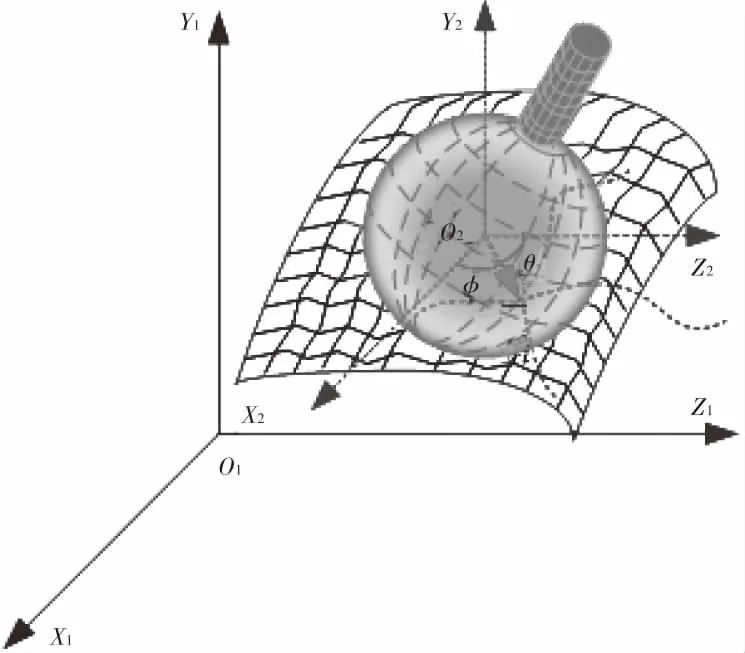
圖5 切點計算空間模型

(3)

式中，r0是球體的平均半徑，k、m是經緯度中的諧波數，ak、am、φk、θm是諧波的振幅和初始相位。

通過將方程組(1)和(2)的右側相等，可得出：

(4)

由式(4)可以得到法向與名義面和球面相交點的坐標。如式(5)：

(5)

在坐標軸上的投影中，法向方程的形式為(式中，u、φ是零件標稱表面的曲線參數)：

(6)

結合公式(5)和(6)可得出：

(7)

對(7)式用數值方法進行求解。將計算出來的參數θ和φ的值帶入(2)式中，計算球面上點的笛卡爾坐標。假設用實線表示實際的復雜曲面，虛線則表示標稱表面。分別計算從球體上的第i個接觸點到零件標稱表面的距離δi。從得到的δi值中，選擇與實際接觸點對應的最小值。

上面提出的數值方法收斂的條件可以歸納為：1)被測量表面不存在奇異點；2)被測曲面曲率小于測球曲率。在實際測量實驗中，可以對測頭進行正確選擇以達到這些條件。本文所提出算法的優點明確，對于復雜曲面測量測點位置分布不均勻的問題，測頭探測的精度以及收斂性不受其影響。

3 實驗驗證

通過實驗測量凸輪輪廓以及測量圓環形標稱表面的滾珠軸承內圈，成功地測試了球形探針半徑補償形狀誤差的方法。坐標測量機作為一臺高精密的測量系統，它對于環境因素(空氣、溫度、濕度)要求非常高。因此本文中CMM安放在精密恒溫箱內，高精密恒溫箱本身放置在一間溫度變化在20 ℃±0.05 ℃、相對濕度值(RH)為50%的恒溫室內。這樣做的目的是盡量減小外界因素對CMM測長系統的影響，以便提高微納米三坐標測量機的穩定性情況。坐標測量機的體積誤差為1.76+L/332 μm，探頭長度為58 mm，探頭球體直徑為1.89 mm。CMM將測量結果保存為探頭球體中心點的坐標。根據CMM軟件中的標準算法和自行開發的MATLAB算法對數據進行處理。

凸輪輪廓經三坐標測量機測量后，以文本文件格式輸出，直接讀取測量結果，可以根據需要設定直角坐標或極坐標輸出。表1以及表2為得到的紅寶石測球中心點的坐標及測頭經過補償后的被測輪廓點的坐標，以直角坐標的形式顯示，補償后的點形成的輪廓線即為凸輪的實際廓線。

從表1以及表2可以看出，補償后實際輪廓線點的坐標更加準確。將上述數據讀入相關工程軟件，即可快速得到凸輪的實際表面廓線。然后根據軟件的功能，可以根據需要與理論廓線進行比較，或做出所需的零件三維實體模型，快速直觀地了解產品的形狀，為設計制造提供可靠的理論依據。如圖6所示的是在軟件中表示的凸輪輪廓線，外側的曲線為測量形成的測頭球心軌跡線，內側的曲線為測頭直徑經過補償以后的凸輪實際輪廓線。如果凸輪為內凹型，則應向外側補償測頭半徑，以得到實際的凸輪輪廓線。

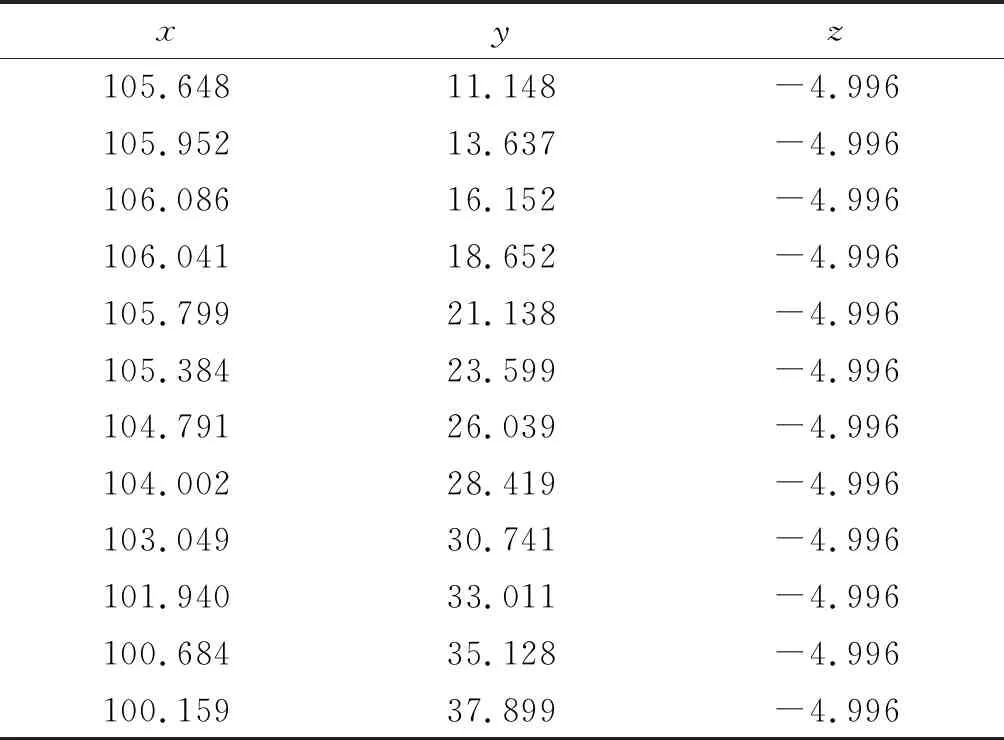
表1 測頭中心點坐標(單位：μm)

表2 補償后實際廓線點的坐標(單位：μm)

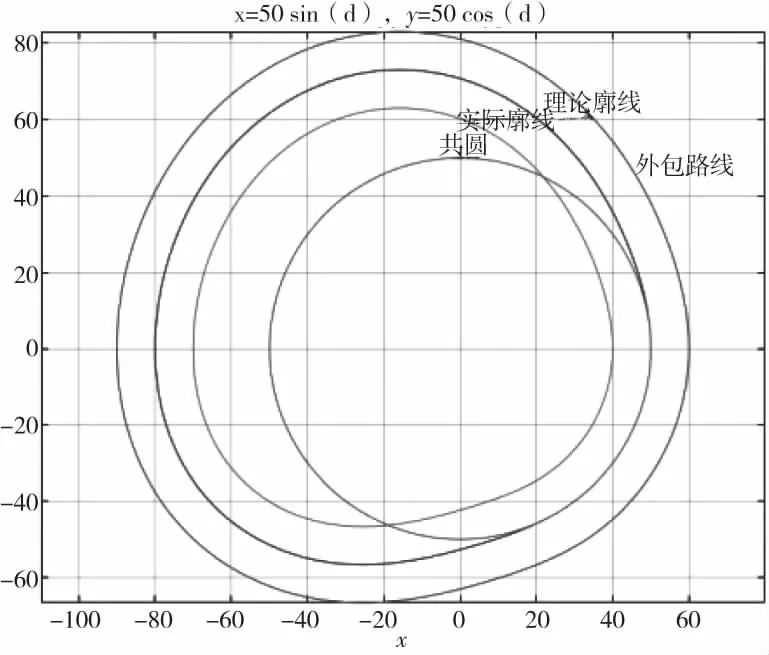
圖6 凸輪輪廓線

圓環體經三坐標測量機測量后，根據標準算法與本文提出算法所測得的形狀誤差數據擬合圖如圖7和圖8所示。

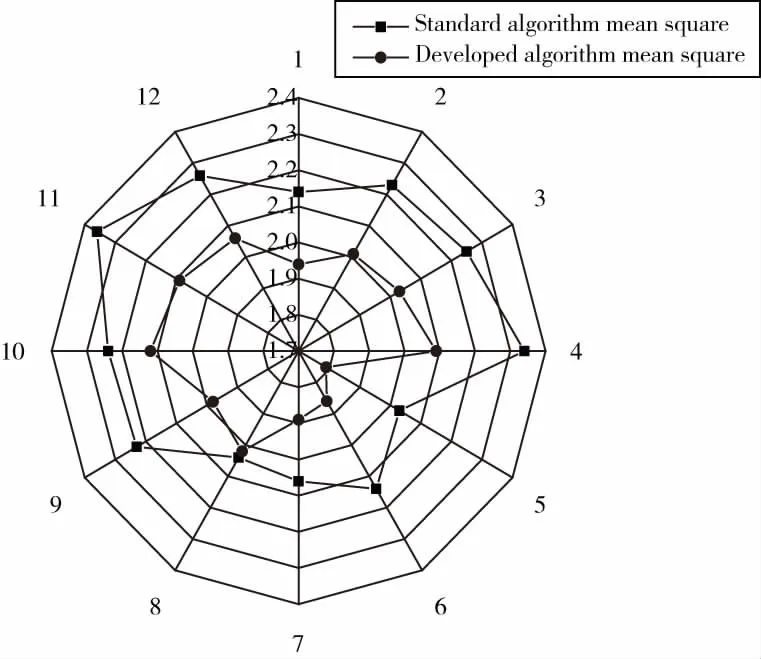
圖7 圓環體被測量表面形狀誤差均方差對比

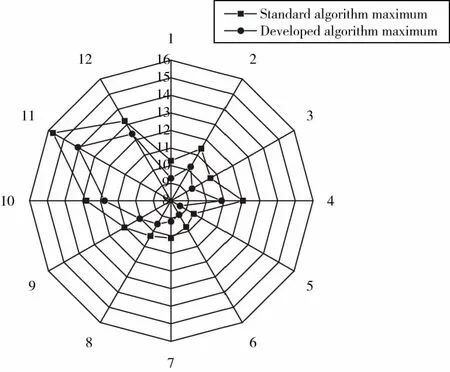
圖8 圓環體被測量表面形狀誤差最大值對比

由圖7和圖8中的數據分析表明，本文所提出的算法在考慮了探頭球體形狀的情況下，所得出的測量結果誤差小。在圓環體的12個被測截面中，標準算法的形狀誤差在9.48～15.71 μm之間，改進算法的形狀誤差在8.59～14.08 μm之間，采用新的數學模型和數據處理算法，使測量誤差平均降低了11.88%。

4 結果分析

本文建立了一種新的球頭與零件表面接觸點的數學模型和數值算法。研究過程中充分考慮球面探針的形狀，可以減小復雜曲面的測量誤差。該算法的核心思想是球面上的點陣列在法向上與標稱表面的距離最小。實驗測量凸輪輪廓以及測量圓環形標稱表面的滾珠軸承內圈，成功地模擬出凸輪輪廓線形狀。通過對滾動軸承內圈環面測量算法的驗證，表明該算法可以將形狀誤差降低11.88%。實驗成功地測試了球形探針半徑補償形狀誤差的方法。因此，所建立的數學模型將有助于在CMMs上測量復雜而精密的曲面，進一步闡明了測頭補償技術的核心問題與關鍵技術，具有較強的實用性，將對曲線、曲面的測量具有重要的意義。