主跨330 m某高速公路雙塔斜拉橋成橋索力確定與穩定性分析

楊 芬，張 華

（湖北省城建設計院股份有限公司，湖北 武漢430051）

1 工程概況

某高速公路主橋為預應力混凝土雙塔三跨斜拉橋，整幅布置，半飄浮體系。主梁采用預應力混凝土雙邊梁，梁高3.4 m，主塔采用薄壁空心花瓶型索塔，橋面以上塔高96 m,單塔設置48對斜拉索。過渡墩及輔助墩為空心墩。主梁標準橫斷面頂板厚30 cm，底板厚50 cm，腹板厚40 cm，橋面設2%雙向橫坡，橋面外側拉索區寬度為150 cm，其中檢修道寬85 cm，單側行車道寬15 m，包含3個行車道和1處應急車道，中央分隔帶寬50 cm。該橋總體布置圖和主梁標準斷面見圖1和圖2。

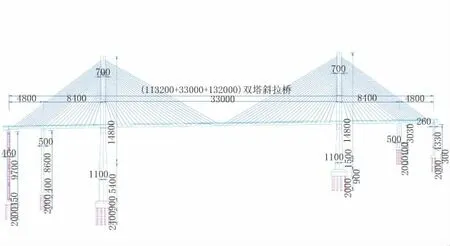
圖1 雙塔斜拉橋總體布置圖（單位：cm）

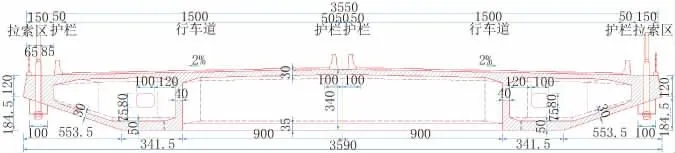
圖2 主梁標準斷面圖（單位：cm）

2 材料參數與模型建立

本橋主梁采用C55混凝土，主塔采用C50混凝土，材料指標取值見《公路鋼筋混凝土及預應力混凝土橋涵設計規范》（JTG 3362—2018）[1]，鋼筋混凝土容重取γ=26 kN/m3，泊松比ν=0.2。混凝土主梁預應力規格采用φs15.2-16和φs15.2-25，兩端張拉，張拉控制應力為1 395 MPa。

采用Midas/civil有限元軟件建立了本橋桿系有限元模型，建模時主梁和索塔均采用空間梁單元建模，拉索采用桁架單元模擬，考慮拉索的垂度效應[2]。全橋共包含686個節點，671個單元。其中包含302個梁單元、177個主塔單元和192個拉索桁架單元，拉索端部與主梁剛接模擬。桿系有限元模型見圖3。

圖3 全橋桿系有限元模型

3 成橋索力確定

采用最小彎曲能法，將索塔和主梁截面抗彎慣性矩Iy縮小為10-5倍[3]，得到全橋截面上下緣應力見圖4。

圖4 全橋截面應力（單位：MP a）

主梁和主塔應力均為壓應力作用，其數值較小，滿足規范限值要求，表明基于最小彎曲能法得到的成橋狀態是合理的。提取最小彎曲能法所得到的成橋索力，對局部索力變化較大處調勻和優化，得到邊跨和中跨優化前后索力見圖5。

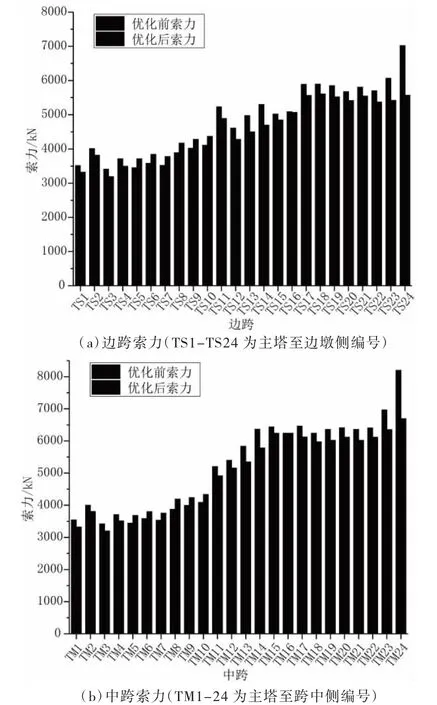
圖5 全橋索力（單位：kN）

采用優化后的索力，計算表明主梁和主塔應力仍滿足規范要求。

4 分析結果

采用無應力索長進行模型正裝施工過程分析，全橋共劃分為59個施工階段，應力驗算組合為：支座沉降+恒荷載+收縮徐變+車道荷載+系統溫度+梯度溫度。同時進行了主梁撓度驗算，結構動力特征值分析和成橋全過程穩定性分析。

4.1 應力驗算

各荷載均取標準值，汽車荷載考慮沖擊系數，主梁截面上、下緣混凝土正應力見圖6。

圖6 主梁截面上下緣混凝土正應力（單位：MP a）

主塔主要受軸壓作用，截面最大壓應力見圖7。

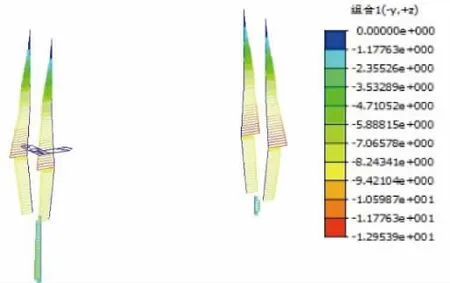
圖7 主塔截面正應力（單位：MP a）

計算表明：主梁截面最大壓應力為16.8 MPa，小于0.5 fck=17.75 MPa，主塔最大壓應力為13.0 MPa，小于0.5 fck=16.2 MPa，且截面均未出現拉應力，滿足規范要求。

4.2 撓度驗算

車道荷載作用下結構豎向變形見圖8。主梁最大豎向撓度位于主跨跨中位置，其數值為12.9 cm≤330/500=66 cm，滿足規范要求[4]。

圖8 全橋豎向變形（單位：mm）

4.3 特征值分析

全橋前4階振型圖見圖9。

圖9 全橋前4階振型圖

全橋前4階振型動力特性見表1。

表1 主橋動力特性

經以上振型分析，豎向基頻為全橋2階振型模式，此時豎向基頻為0.40 Hz，參考《公路橋梁抗風設計規范》（JTG/T 3360-01-2018）式6.3.1-2[5]，該公式估算基頻為：150/L=0.45 Hz。模型豎向基頻與規范估算公式較為接近，表明該橋動力特征基本合理。

4.4 穩定性驗算

穩定性分析主要分析三種不利工況。工況1：裸塔，荷載為自重+風荷載；工況2：最大懸臂，荷載為自重+風荷載；工況3：成橋運營，荷載為自重+二期+風荷載+塔底軸力最不利時的汽車荷載，各工況荷載均取標準值，計算結果見圖10。

圖10 穩定性分析計算結果

計算表明：裸塔工況下，穩定安全系數為21.7≥4，空間穩定性滿足要求，相應失穩模態表現為索塔縱向失穩；最大懸臂狀態下（中跨合攏前），穩定安全系數為8.3≥4，空間穩定性滿足要求，相應失穩模態表現為索塔縱向失穩、主梁豎向失穩；成橋運營工況下，穩定安全系數為9.7≥4，空間穩定性滿足要求，相應失穩模態表現為索塔縱向失穩、主梁豎向失穩。

該橋穩定驗算控制工況為最大懸臂狀態，相似橋型施工時應采取必要措施保證該狀態穩定性滿足規范要求。

5 結 語

本文通過對某高速公路132 m+330 m+132 m雙塔斜拉橋建模計算分析，通過最小彎曲能法得到了成橋索力，在此基礎上驗算了結構的應力、撓度、動力特性和及穩定性，各項驗算結果表明結果安全可靠，結構動力特征較好，施工狀態下和成橋運營下均不發生失穩破壞。