大跨徑小半徑曲線橋梁轉體結構設計

陳愛榮

［上海市政工程設計研究總院（集團）有限公司，上海市200092］

0 引言

橋梁轉體施工按旋轉方向可分為平轉法、豎轉法以及平豎轉相結合的工法[1]。一般平轉法橋梁平面線形通常為直線或大半徑曲線。近年來，逐步出現了小半徑曲線橋梁的轉體施工，相比之下，小半徑曲線橋梁的轉體結構設計更復雜。對于跨徑較大的橋梁，轉體結構的穩定性往往成為設計關注的重點。本文以寧波市軌道交通4號線跨鐵路轉體橋為例，介紹大跨徑小半徑曲線懸澆橋梁轉體結構的設計要點。

1 工程概況

寧波市軌道交通4號線在右轉出江北大道后，小角度（約30°）斜交上跨蕭甬鐵路、杭甬客專，線路曲線半徑僅350 m。

跨鐵路節點橋現狀橋位見圖1。

圖1 跨鐵路節點橋現狀橋位

蕭甬鐵路交叉段為路基段，采用混凝土軌枕，有碴軌道；杭甬客專為高速鐵路，設計時速350 km/h，交叉段為高架橋，總寬約12 m。為了減小本工程對既有線路的影響，橋梁方案采用跨徑布置為68 m+138 m+95 m=301 m的預應力混凝土剛構橋，主跨1孔跨越現狀鐵路，北側承臺邊緣（墩號QJ01D027）距蕭甬鐵路中心線9.1 m，南側承臺邊緣（墩號QJ01D028）距杭甬客專中心線20.9 m，滿足鐵路保護施工安全距離要求。先在鐵路兩側澆筑橋墩及主梁，澆筑完畢后，進行轉體施工，轉體就位后合龍成橋。

跨鐵路節點橋平面布置如圖2所示。

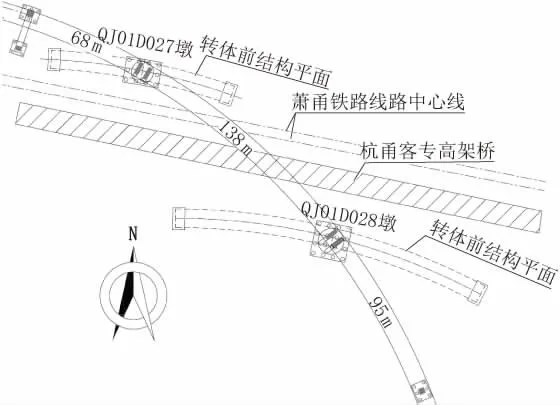
圖2 跨鐵路節點橋平面布置圖

2 主要技術標準

（1）最高運行速度v=80 km/h。

（2）車輛：B型車，6輛編組，軸重不大于14 t。

（3）線路：雙線，線間距為4.2 m。

（4）橋梁寬度：11 m。

（5）設計使用年限：100 a。

3 轉體結構設計

3.1 總體設計

轉體結構由上轉盤、球鉸、下承臺、轉體牽引系統組成[2]。在轉體過程中，上轉盤、下承臺通過球鉸傳力，呈現多維受力狀態，均需布置雙向多層預應力鋼束。

QJ01D27墩轉體質量約7 700 t，T構總長100 m，轉體角度19°，上轉盤平面為φ12 m圓形，厚2.5 m，下承臺平面為14 m×19.4 m矩形，厚3.5 m，下設12根直徑2.0 m鉆孔灌注樁基礎；QJ01D28墩轉體質量約14 600 t，T構總長172 m，轉體角度40°，上轉盤平面為φ15 m圓形，厚3.0 m，下承臺平面為19.4 m×19.4 m矩形，厚4.0 m，下設16根直徑2.0 m鉆孔灌注樁基礎。上轉盤、下承臺間布置撐腳及砂箱，轉體完成后澆筑厚0.8 m的封鉸混凝土。

轉體牽引系統由中心對稱的2束鋼絞線組成，鋼束錨固于上轉盤內部，如圖3所示。QJ01D027墩轉體啟動牽引力739 kN，選用11-φs15.2鋼絞線，啟動時鋼絞線應力480 MPa，安全系數為3.8；QJ01D028墩轉體啟動牽引力1 511 kN，選用21-φs15.2鋼絞線，啟動時鋼絞線應力514 MPa，安全系數為3.6。

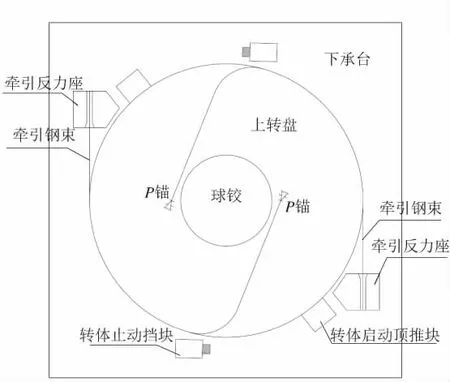
圖3 轉體牽引系統示意圖

3.2 球鉸的選用

球鉸一般采用廠家成套產品，可以根據轉體噸位確定球鉸的材料及尺寸。

球鉸材料有鋼材及混凝土2種，混凝土球鉸一般適用于轉體噸位6 500 t以下的橋梁，本橋轉體噸位較大，故選用鋼球鉸。

根據轉體噸位，可按表1選用球鉸的磨心支承半徑R1，再按表2選用球鉸的半徑R。

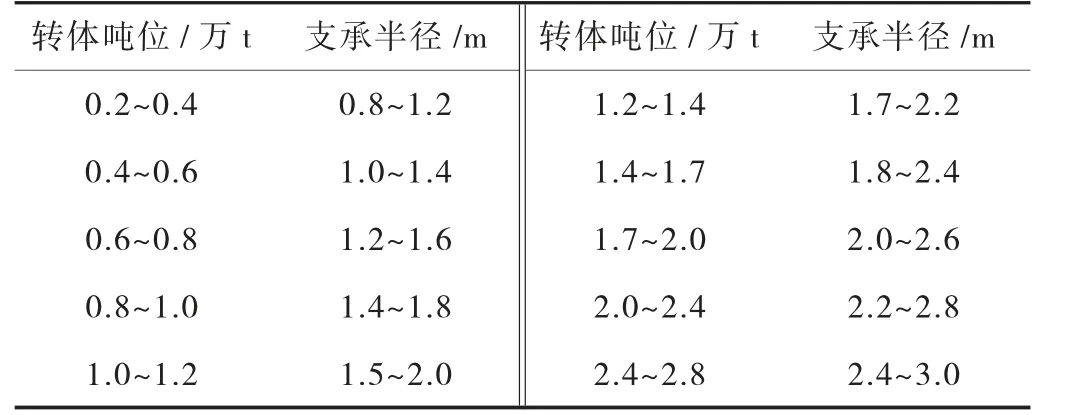
表1 不同轉體質量下的球鉸支承半徑取值范圍

表2 不同支承半徑的球鉸半徑取值范圍

本橋轉體墩位分別為7 700 t和14 600 t，故相應的球鉸磨心支承半徑R1和球鉸半徑R分別選用1.5 m、7 m和2 m、8 m，設計過程中實體建模分析，保證球鉸在轉體時全程受壓且不被壓壞。

3.3 轉盤中心預偏設置

曲線橋上部結構自重會引起橫向不平衡彎矩。本橋位于小半徑曲線上，最大懸臂狀態下墩底橫向偏心彎矩QJ01D027墩為50 085 kN，QJ01D028墩為251 410 kN，偏心彎矩過大。配重平臺因配重量小，力臂較短而平衡偏心彎矩能力有限，故需通過設置轉盤中心預偏以抵消曲線梁上部結構恒載橫向偏心。橫向預偏值可通過墩底橫向不平衡彎矩除以轉體質量求得，方向與橫向不平衡彎矩引起的偏心方向相同。

通過計算，本橋QJ01D027墩轉盤中心設置0.8 m橫向預偏心，QJ01D028墩轉盤中心設置2.5 m橫向預偏心，橋墩采用矩形空心截面，橫向立剖面單側變寬以調整偏心，如圖4所示。

圖4 轉盤中心預偏設置示意圖（以QJ 01D027墩為例）（單位：mm）

3.4 懸澆階段穩定性分析

轉盤中心橫向預偏為基于T構施工至最大懸臂狀態時設置，對于施工至各節段的懸臂狀態則會存在與偏心設置方向反向的彎矩；考慮懸臂澆筑施工的先后順序、風荷載的方向、施工機具的布置等因素也會造成荷載的不對稱，故需對懸澆各節段的抗傾覆穩定性進行驗算。

3.4.1 計算模型

采用計算軟件Midas/Civil建立懸澆階段曲線桿系模型，進行懸臂澆筑施工模擬。下部結構建至上轉盤為止，在球鉸位置處施加固結邊界條件，計算模型如圖5所示。

圖5 懸臂澆筑階段模型（以QJ 01D027墩為例）

3.4.2 計算荷載

計算荷載主要考慮引起懸澆階段轉體結構傾覆風險的荷載。

自重：混凝土容重按26 kN/m3計算，軟件自動計算。

風荷載：分別考慮9級風（25 m/s）與百年一遇風（31.3 m/s）在施工過程中引起的橫向風荷載、縱向風荷載以及風舉力。風舉力P=CLwA，式中：w為基本風壓；A為水平投影面積；CL為風舉力系數，取0.75[3]。

掛籃荷載：取懸臂施工最大節段質量的40%計算，作用點位于下一節段中間位置。

施工誤差荷載：考慮施工節段時產生±2.5%的質量誤差。

3.4.3 工況組合

3個因素在Y1模型上對F值的響應值的影響由大到小依次為：一次項>二次項>交互項，由P值可以看出一次項對實驗結果的影響是極顯著的；3個因素在Y2模型上對F值的響應值的影響由大到小依次為：二次項>一次項>交互項，從P值反映的結果來看，實驗結果受二次項影響較為顯著，交互項對結果的影響相對較弱。由回歸P值可以看出，Y1模型顯著，Y2模型極顯著，說明由這2個模型代替實際實驗點進行分析途徑可行，結論可信。

假定轉體結構縱橋向重心線兩側分別為A、B側，橫橋向重心線兩側分別為C、D側，如圖6所示。

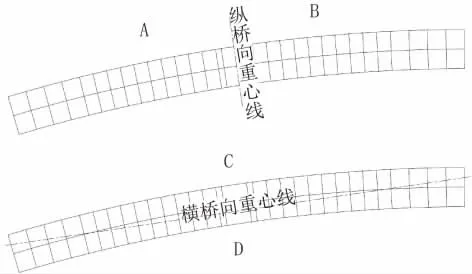
圖6 轉體結構重心線劃分

驗算懸臂澆筑階段抗傾覆穩定性時考慮如下4種荷載工況：

（1）A側恒載重102.5%+B側恒載重97.5%+對稱掛籃+A側箱梁多澆筑1/2節段+A側有50 kN施工機具+順橋向9級風載+B側風舉力。

（2）A側恒載重102.5%+B側恒載重97.5%+對稱掛籃+順橋向百年一遇風載+B側風舉力。

（3）C側恒載重102.5%+D側恒載重97.5%+對稱掛籃+A側箱梁多澆筑1/2節段+A側有50 kN施工機具+橫橋向9級風載。

（4）C側恒載重102.5%+D側恒載重97.5%+對稱掛籃+橫橋向百年一遇風載。

工況（1）、工況（2）為縱橋向重心線單側最不利布置工況；工況（3）、工況（4）為橫橋向重心線單側最不利布置工況。

3.4.4 結果分析

轉體結構抗傾覆失穩力矩為T=R’×F，其中：R’為球鉸體系的環道半徑；F為轉體結構球鉸以上部分的總重。提取4種工況下施工每個節段時球鉸底部的軸力F以及2個方向的彎矩Mx、My，計算合彎矩M=（Mx2+My2）×0.5，即可求得抗傾覆穩定系數k=T/M=R’×F/M，如圖7所示。

圖7 懸澆階段抗傾覆失穩圖示

QJ01D27、QJ01D28墩在4種荷載工況下施工每個節段時抗傾覆穩定系數的變化規律如圖8、圖9所示。

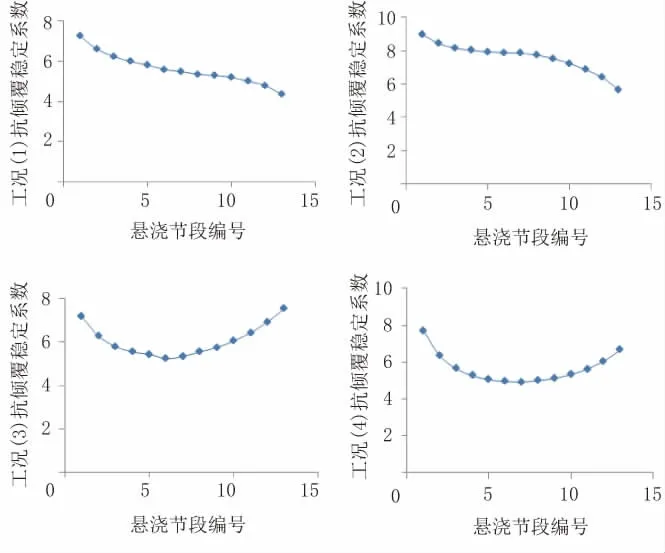
圖8 QJ 01D27墩各工況下抗傾覆穩定系數變化圖

圖9 QJ 01D28墩各工況下抗傾覆穩定系數變化圖

由圖8、圖9可知，本橋4種最不利工況下，懸澆階段結構的抗傾覆穩定性均能滿足規范要求。分析抗傾覆穩定系數隨懸澆節段的變化規律發現，縱向不平衡荷載作用下（工況（1）、工況（2）），抗傾覆穩定系數整體呈現正弦曲線變化規律，最小值在1/4跨或全跨附近；橫向不平衡荷載作用下（工況（3）、工況（4）），抗傾覆穩定系數呈現近似拋物線變化規律，先減小再增大，最小值在1/4跨或半跨附近。對于懸澆階段結構的抗傾覆穩定性驗算，本文推薦選取懸澆至1/4跨、半跨以及全跨時的受力狀態進行計算分析。

3.5 轉體階段穩定性分析

轉體結構除了要滿足懸澆階段的抗傾覆穩定性要求，還需滿足轉體階段的抗傾覆穩定性要求。轉體過程中，球鉸發生如圖7所示的傾覆失穩模式，以撐腳為軸發生傾覆失穩。

傾覆荷載考慮9級風（25 m/s）在施工過程中引起的橫向風荷載、縱向風荷載以及風舉力，上部恒載剩余偏心按配重調偏后0.2 m計，并考慮撐腳下移10 mm引起的重心附加偏移。撐腳與環道的幾何相對位置如圖10所示[4]。

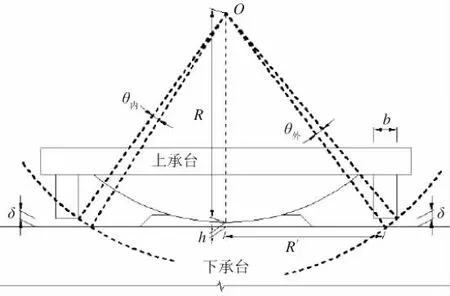
圖10撐腳與環道的幾何相對位置關系

圖10 中參數間有如下關系：

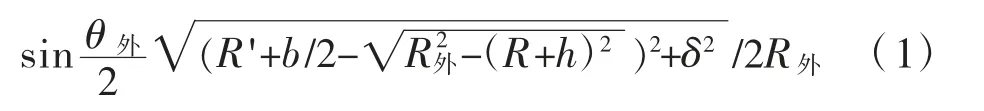
式中：R外為撐腳外邊緣的旋轉半徑，其表達式為：

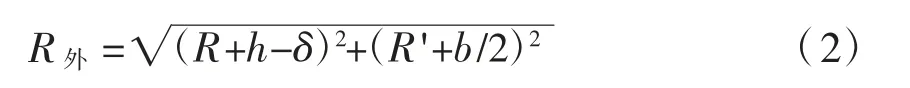
轉體結構的重心位置偏不利地取于梁頂，通過撐腳下移值10 mm計算得到球鉸發生的轉角θ外，可得重心附加偏移值：

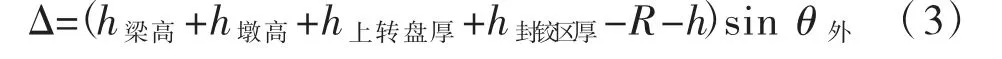
分別計算轉體階段橫向和縱向的抗傾覆穩定系數。橫向風荷載及相應風舉力引起的傾覆彎矩為M橫，縱向風荷載及相應風舉力引起的傾覆彎矩為M縱，則轉體階段的橫向抗傾覆穩定系數k橫、縱向抗傾覆穩定系數k縱分別為：

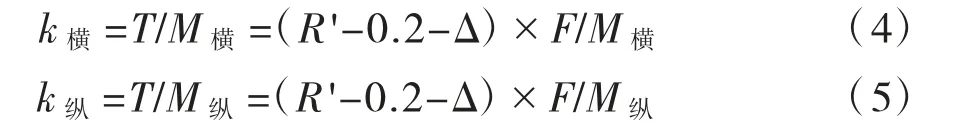
本橋轉體階段QJ01D27墩橫向抗傾覆穩定系數k橫為32.7，縱向抗傾覆穩定系數k縱為56.3；QJ01D28墩橫向抗傾覆穩定系數k橫為42.7，縱向抗傾覆穩定系數k縱為75.0，均能夠滿足抗傾覆穩定要求，且富余很大。分析結果不難發現，設置轉盤預偏及配重調偏后的轉體結構，不平衡彎矩已大大降低，只需施工精度控制得當，一般不會發生轉體階段的傾覆失穩。

4 結 語

本文基于寧波市軌道交通4號線工程跨鐵路轉體橋，從轉體結構的總體組成、球鉸的選用、轉盤預偏心的設置、懸澆階段結構的穩定性、轉體階段結構的穩定性等方面闡述了大跨徑小半徑曲線轉體橋轉體結構的設計要點、計算方法等，總結了此類橋梁懸澆階段結構的抗傾覆穩定性規律，提出懸澆階段結構的抗傾覆穩定性驗算關鍵節點為施工1/4跨節段、半跨節段以及最終節段；轉體階段結構的抗傾覆穩定性系數一般富余較大，不會發生轉體階段的傾覆失穩。所得結論可為同類工程項目提供參考。