基于復雜網絡理論的城市供排水系統規劃優化

龍 霞，朱建樹

（1.中國市政工程西南設計研究總院有限公司，四川 成都610000；2.中國市政工程中南設計研究總院有限公司，湖北 武漢430000）

0 引言

城市供排水系統屬于典型的復雜網絡架構。四線以上城市的供排水系統一般存在多個水源設施、多個污水處理設施、多個雨水泄出系統，即城市供排水系統屬于多個相互關聯、相對獨立、相互制約的供水網絡、污水網絡、雨水網絡的集合體[1]。分析城市供排水系統的性能，找到其中的薄弱點，從而獲得供排水系統持續優化過程中的重要步驟[2]。

早期的城市供排水系統規劃優化過程，多將城市供排水網絡中的供水網絡、污水網絡、雨水網絡分別進行設計規劃，甚至將多個子系統分別進行設計規劃，使得城市供排水系統被化成孤立的多個構成部分。這種規劃方式難以充分發揮城市供排水網絡設施的最大效能，使部分設施冗余閑置、部分設施超負荷運行[3]。

復雜網絡理論是一種基于網絡結構熵與特征譜的網絡評價體系，將城市供排水系統看作一個整合網絡，對其結構熵和特征譜做出評價，在所有優化方案中選擇對其結構熵與特征譜優化效果最佳的方案，從而做出最大限度的城市供排水系統規劃優化[4]。

之前的復雜網絡理論在電網、交通網、社會關系網、生物新陳代謝網絡中有較多應用，但在供排水系統中的相關文獻并未出現在包含知網、萬方、龍源等在內的常規文獻中，即本文研究的復雜網絡理論在城市供排水網絡中的應用屬于基礎理論的應用空白。因此，這是本文研究的最大創新點[5]。

1 復雜網絡理論中的結構熵與特征譜

復雜網絡理論的本質是分析非典型拓撲結構網絡的混亂度和自組織性，進而得到網絡的紊亂度和穩定性。復雜網絡理論并不將網絡的拓撲結構和成樹方法作為核心關注點，而是考慮網絡中較深層次的運轉狀態和流量性能[6]。在復雜網絡理論中，應首先確立網絡的非拓撲視角結構特征，一般從其積累度分布特征進行模型搭建。

冪率分布關系下：

式中：P（k）∝k-v，v為冪率指數，此時網絡的累積度分布函數符合冪函數的v-1冪率分布關系；

式中：P（k）∝e-k，此時網絡的累積度分布函數符合自然常數指數的分布關系。

在對應的復雜網絡累積度結構的基礎上，可以進行網絡的密度、介入度、距離分布等計算。因為這些量化指標均為簡單累加或算數平均關系，所以受限于本文篇幅，不在此進行深入函數分解分析。該研究對供排水網絡的復雜網絡分析中使用到的其中最重要的兩個評價指標，是供排水網絡的結構熵和特征譜。

網絡結構熵可定義為節點的重要度分布熵，如公式（3）：

式中：ki為累積度評價中第i個節點的k值；N為模型考察的節點數。

在節點重要度評價Ii指標的基礎上進行數據整合，可以得到網絡的整體結構熵，如公式（4）：

式中：相關數學符號同前文各公式。

早期相關機構對復雜網絡模型進行研究過程中，特別是在社會關系網絡的研究中，發現封閉社會關系網絡中存在多個節點之間的互通聯系顯著高于其他網絡節點。這些節點代表的自然人節點多為社會關系網絡封閉網絡中的“富人”群體，故提出了復雜網絡的富人俱樂部模型（Rich-Club）。在后續研究中發現這一模型在其他類型網絡中同樣適用。當前，該模型多用于在結構熵指標基礎上進一步分析網絡的特征譜結構。

Rich-Club模型的基函數可寫作公式（5）：

式中：將復雜網絡分為r個子區域，研究子區域的整體結構熵Er，同時對復雜網絡體系中存在的r個子區域按照上述公式建立均值構型，從而得出Rich-Club模型評估結果φ（r）。

2 復雜網絡理論對供排水網絡的實際意義

2.1 城市供排水系統一般模式

城市供排水系統一般需要滿足3個網絡功能。從水源井中汲取的飲用水水源，經過自來水設施充分凈化后，由自來水網絡向住戶處進行供水，其間經過多次加壓以滿足住戶的用水需要[7]。住戶生產與生活產生的污水，經過分布式的社區污水池初步匯聚并沉淀后，經過多次加壓，經歷分布式污水處理設施后，匯總到區域中心的污水處理設施。處理達標后，進行污水排放處理[8]。污水排放一般分為3個方向，高標準處理后的污水，可以達到自來水水源級別的，可以直接向自來水設施進行供水，但大部分城市當前缺少該污水處理技術。如果區域中心污水處理設施緊鄰排水口，其他污水可以直接向排水口排出；無此條件的，可以通過雨水排放設施向排污口進行排水，詳見圖1。

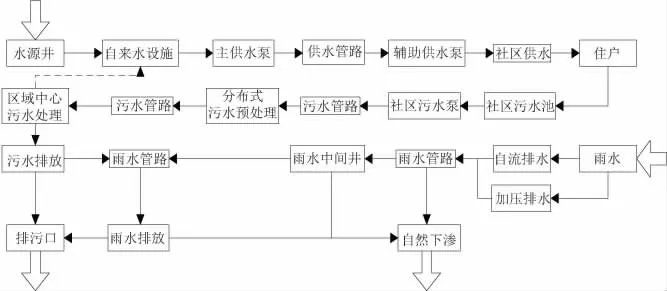
圖1城市供排水網絡一般模式

圖1 中，系統內水源主要有兩個：一是水源井的水源汲取系統，二是城市區域內的雨水匯聚收集系統。系統內排水設施也主要有兩個方向：一是在雨水排污過程中通過自然下滲向淺層地下水排放，二是通過排污口向地面徑流排放。城市供排水系統的復雜度主要來自網絡節點的并發性，即在系統中存在多個住戶節點。對一般城市來說，該節點數量可能達到數萬至數十萬個，且水源井、社區污水池、分布式污水預處理設施、區域中心污水處理設施、雨水中間井、排污口等，均存在多個并行設施。這些并行設施在相應網絡的驅動下，會將城市供排水設施劃分為多個子系統。這些子系統功能上相對獨立，均有能力獨立完成對應功能，但在拓撲上又彼此互聯、互為補充。所以，城市供排水網絡難以實現傳統拓撲視角下的拓撲分析[9]。

2.2 城市供排水系統的結構熵與特征譜

分析城市供排水系統的結構熵與特征譜的統計學意義是：其結構熵代表了城市供排水系統的復雜度，同時約束了城市供排水系統的網絡流量交叉程度。其特征譜的統計學意義為：分析城市供排水網絡中的網絡主干顯著程度、特征譜評價指標較高的網絡存在顯著的網絡干線提供網絡主干功能。而結構熵與特征譜均屬于熵值指標或熵值累加、熵值均值指標，低于1.000的評價結果表明相關統計學表達較弱，而高于1.000的評價結果表明相關統計學表達較強[10]。

從城市供排水系統網絡的規劃優化視角出發，降低其結構熵并提升其特征譜有助于使網絡發揮出更大作用。而結構熵與特征譜屬于相互制約關系，在較低結構熵條件下難以獲得更高特征譜。所以，應對方案之間的結構熵、特征譜評價結果進行比較，或在時間線上評價單一方案的結構熵、特征譜表達結果，單純查看單一方案的結構熵、特征譜評價結果，而非進行上述橫向或縱向比較，則該兩個數據沒有統計學邏輯意義。

3 個案條件下的供排水網絡復雜網絡分析

3.1 個案基本情況

某城市城區常住人口204萬人，63萬戶。另有工業用水用戶1 079戶，商業用水用戶476戶，城市面積132 km2。當前擁有水源井9個，沿河排污口3個，區域中心化污水處理設施5個，雨水中間井12個。供排水系統升級前，該市用水用戶社區接入口供水水壓0.63±0.14 MPa，低于國家相關標準要求的0.70 MPa標準。城市內澇（＞150 mm）超出城市面積15%范圍的天數約為4.3±0.2 d/y，相對于地區其他省市，該指標略顯優勢。3個沿河排污口經過持續定期抽檢，未發生污水排放污染物超標現象。

技術升級過程中分析發現，城市供水水壓偏低的核心原因，是自來水供應水量小于城市用水需求水量。當前9個水源井汲取量為750~800 kt/d，實際居民全壓供水能力為每戶0.8~0.9 t/d，而居民實際用水需求超過每戶1.2 t/d。該供需矛盾是該市供水能力的核心矛盾。所以，加大自來水水源汲取量是解決該問題的關鍵。

3.2 網絡升級規劃方案的比較結果

為實現上述個案需求，該市規劃3個新建水源井并建設配套自來水處理設施，同時鼓勵工業用水企業與自來水公司合建專用小規模水源井。傳統方案分析路徑下，必然出現3個新建水源井同時投入條件下獲得最大供水能力的結果，所以本文研究3個新建水源井的開工量與城市供排水網絡結構熵與特征譜之間的統計學關系（見表1）。

表1 城市供排水網絡新建水源井數量與復雜網絡特征的關系

表1中，因為該城市供排水網絡優化策略的多目標優化體系，其核心目標是結構熵的降低和特征譜的增加。受制于供水能力提升后的污水、雨水排水能力制約，其結構熵除新建A+C井方案和新建A+B+C井方案結構熵出現增加外，其余所有方案均出現了結構熵降低；而所有方案的特征譜均出現了增加。所以，單純考察多套方案的結構熵與特征譜變化情況，無法對相關方案作出有效選擇。本文在結構熵、特征譜變化趨勢的基礎上，進行了數據深度挖掘，以求發現在結構熵熵減最大幅度的基礎上，選擇特征譜的最優表現。其數據處理策略詳見圖2。

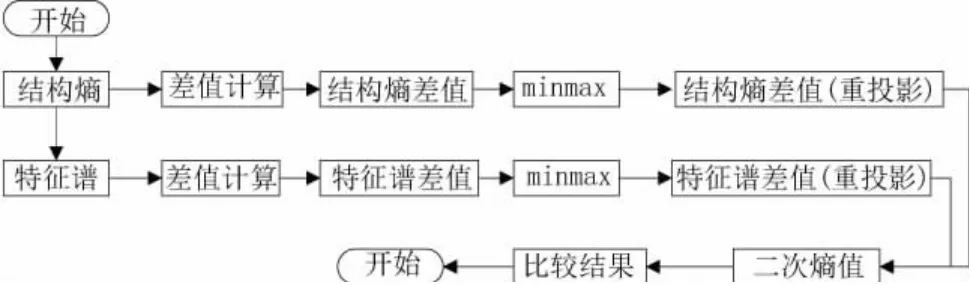
圖2結構熵及特征譜的二次處理流程

圖2 中，特征譜解算結果來自結構熵計算結果，詳見公式（4）與公式（5）的代入關系。差值計算結果已在表1中得出，而minmax計算方法與二次熵值計算方法，詳見公式（6）：

式中：Xi為該列數據中的第i個輸入值；min，max分別為該列數據的最小值與最大值。minmax算法的統計學意義是將上述結構熵差值與特征譜差值在[1，2]區間上進行重投影。其中，最小值投影為1.000，最大值投影為2.000。之所以要在傳統minmax模型基礎上加位移常數1，是因為傳統minmax投影區間為[0，1]，單列數據經過處理后必然出現至少一個0值，影響后續的熵值處理。加位移常數1后，其投影區間可以充分避開0值且不影響投影效率。

此時，可產生二次熵值的計算條件，即所有除數與被除數均為非負值。二次熵值是以經過重投影的特征譜差值為被被除數，以結構熵差值為除數，求商值。經過上述治理，可以得到表2數據。

表2中，因為本文個案的多目標需求為結構熵值降低和特征譜值增加，經過求熵計算后，二次熵值最高的方案即平衡上述優化目標的最優結果。實際試算結果中，二次熵值最低為新建A井的0.737，最高值為新建B井的1.151。可見，選擇新建B井而暫時擱置A井與C井建設規劃的網絡規劃優化模式，是當前條件下可以采取的最優模式。

表2 復雜網絡的二次熵值試算結果

4 結語

使用復雜網絡模型對個案城市的3個規劃新建水源井的建設關鍵度進行分析，選擇可啟用的水源井建設項目。通過分析，發現單純使用復雜網絡模型對方案進行分析，其分析結果的特征并不明顯。所以，本文在此基礎上進行算法擴增，引入二次熵值法使其數據特征更加顯著。最終選擇單獨新建水源井B井的方案作為城市供排水方案的規劃優化方案。

該研究的創新點主要有兩點：一是將復雜網絡模型引入供排水網絡的優化過程中；二是為了讓復雜網絡模型更適應城市供排水網絡的分析需求，對復雜網絡模型進行了分析算法的擴增。