基于橋梁結構安全可靠性的車輛載重限值研究

朱 榮

（上海同濟檢測技術有限公司，上海市200092）

0 引言

橋梁的運營維護活動是形成對評估結果的管理對策。除了必要的加固維修以外，對不滿足當前交通狀況的橋梁進行適當的限載也是必要的管養手段。

歐美國家對橋梁通行汽車荷載限值問題的研究起步較早，并制定了符合其本國國情的車輛載重規制。其中，以美國的公路橋梁車輛載重標準體系最為完善。其基于應力超限率法，分別提出了FBF B、TTI和TRB等公式[1-2]作為美國評估規范中法定車輛荷載（Legal Loads）和限定車輛荷載（Posting Loads）的理論依據。

我國的車輛載重標準最早是1982年開展的“交通運輸技術政策研究”。根據當時路網的技術狀況，從1989年實施的《公路工程技術標準》規定了單軸重10 t的限值標準，并作為我國公路、橋梁設計的軸載標準和限載依據沿用至今。

經歷30多年的發展，雖然超重運輸現象嚴峻，但公路橋梁等基礎設施條件有了明顯改善。目前的道路超載認定卻不能準確地為橋梁的限載取值提供可靠的依據，也不利于合理地提升公路橋梁服務水平。為此，國內學者在超載橋梁安全性分析和限載方法等方面開展了相關的研究[3-4]，雖取得了一定的研究成果，但也存在一些不足之處：（1）未能提供橋梁結構安全的限載分析指標，合理的安全指標是構建橋梁限載分析的重要前提；（2）并沒有提出比較完善的限載分析理論，為在役橋梁安全管養提供合理的理論依據；（3）未能形成典型限載車型譜系，為橋梁限載管理提供現實依據。

現通過對實測車輛數據的統計，分析現階段貨車類型及其荷載分布特征，根據各載重車輛的超載情況和對橋梁結構的影響確定橋梁限載的典型車型。然后，以結構可靠性理論為基礎，對基于橋梁安全運營的車輛載重限值分析方法進行研究，明確計算基本步驟。最后，通過算例，介紹本文提出的在役橋梁限載分析的實施過程。該項研究從橋梁結構安全運營的角度建立了車輛限載取值的方法，為重載交通下的橋梁管養提供理論依據。

1 車輛荷載調查及典型限載車型譜系

1.1 運營階段車輛荷載特性

車輛荷載特性包含車重、軸重和軸距在內的描述車輛基本信息參數，是橋梁汽車荷載分析的重要參數，由一些典型車型構成。參考我國汽車制造行業標準，常見的貨運車型大致可以劃分為10種型式，按軸數分類主要包括二軸、三軸、四軸、五軸和六軸等五種類型[5]。通過對車輛荷載數據進行的統計，可充分了解當前路線上的主力車型，各車型構成情況見表1所列。

表1 車型分類及車型組成特性一覽表

可以看出：絕大多數的貨車以二軸和六軸車為主，兩者總和接近所有貨車總量的3/4，其中二軸貨車占48.9%，六軸車占23.7%；三、四軸車代表車型包括自卸車和倉柵式載貨車，占比不大，分別為10.5%和12.5%；五軸車所占比例最小，僅為4.4%，代表車型為裝載能力較小的拖掛車，主要用于重量較輕的貨物運輸。

各車型的車重和超載情況的統計見表2所列，超載車輛的認定基于目前國內的治超標準[6]，車輛超載率按照式（1）計算：

從表2各車型的車重和超載情況分析看，六軸車的兩種車型T-9和T-10，以及五軸的T-6超載車比例較大，且超載問題嚴重，是重型貨車中需重點關注的車型；對于中型載重車，需重點關注四軸的T-4和三軸的T-3車型；雖然兩軸車整體車重水平不高，但由于軸數較少，分擔到單軸的重量較大，對于小跨徑橋梁，過重的軸載也會帶來極大的安全隱患，因此，二軸貨車也需要考慮。

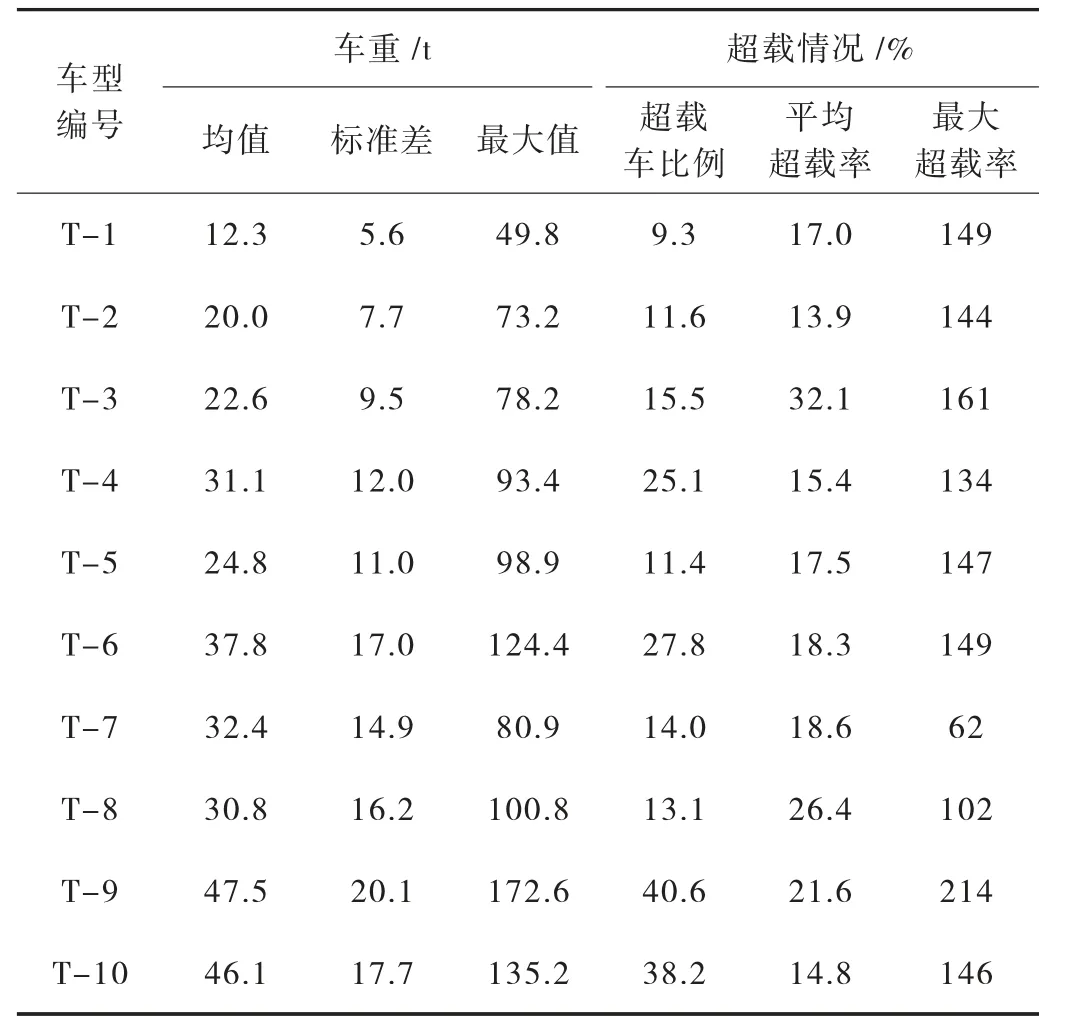
表2 車重和車輛超載情況一鑒表

1.2 典型限載車型譜系

典型限載車型是橋梁限載分析的前提基礎，表1所列代表了目前公路通行的大部分車型，由于車型類別較多，用于橋梁限載分析是相當繁瑣的。為此，需要進行簡化，提煉出一組最具代表性的車型，以此形成橋梁限載的車型譜系。

目前，車輛限載標準的普遍做法是根據軸型車輛（軸數）限制車重。現參考這種限載方式，具體方法如下：

首先，將表1中的10類車按軸數進行歸類，對具有相同軸數的車輛，綜合考慮其數量比例、車重及超載情況和對結構荷載效應等因素，確定一種最具代表性的車型作為限載模型車輛。

例如，四軸車有T-4和T-5兩種車型，其荷載特性的比較見表3所列。從表3可以看出，T-4車型在數量上五倍于T-5，平均車重與超載車比例均大于T-5；而在平均超載率和最大超載率上，T-5略大10%左右。

表3 四軸車T-4、T-5車輛荷載特性比較一覽表

對比兩種車型在相同車重下的簡支梁跨中彎矩和支點剪力效應，如圖1所示。從圖1可以看出，在相同車重下，車型T-4通過橋梁產生的荷載效應大于T-5，說明四軸車中T-4軸重和軸距配置對結構受力不利。綜上分析，選擇車型T-4為四軸車的限載模型車輛。

圖1 T-4、T-5簡支梁效應比較圖（車重Wt=40 t）

其次，確定各代表限載車型的軸距、軸重與總重的分配關系。軸距根據表1統計結果獲得；軸重分配比例利用實測數據中的總重和軸重數據通過線性回歸分析法確定。以T-4車型為例，圖2為該車型軸重與車重關系的線性回歸圖。

圖2 T-4車型車重與軸重的關系圖

從圖2可以看出，軸重線性回歸擬合的可決系數R2在0.75以上，說明軸重與總重比例關系與線性函數評價之間的相關性較好。最終，得到四軸車型的軸重分配比例為0.14∶0.16∶0.35∶0.35。

最后，按照與設計荷載效應等效的原則確定每類模型車輛的標準額定車重。選取公路-I級汽車荷載作用下，中小跨徑橋梁跨中彎矩或支點剪力效應標準值為等效的荷載效應，計算公式為：

式中：WQ為模型車輛額定車重；MD為公路-I級汽車荷載作用下的荷載效應標準值；Mu為模型車輛在單位車重下的荷載效應。

根據上述方法，將表1軸數相同的各類車型進行合并，重新定義成5個車型類別組成的限載車輛譜系，如表4所列。為了使模型車輛的荷載參數簡潔和應用上的方便，車輛軸重取5kN的整數倍，軸距取0.1 m的整數倍。

表4 限載模型車輛額定荷載譜系一覽表

2 基于安全可靠性的車輛載重限值分析方法

2.1 載重限值的可靠性分析方法

結構的可靠性反映的是結構的承載能力與荷載效應間大小的隨機比較，用概率的方法來描述結構完成預定功能的能力。對于既有橋梁的汽車限載分析，是根據預設的目標可靠度和已知的結構承載能力和恒載效應反算出允許通行的最大汽車荷載效應，屬于可靠性反問題的范疇[7]。

所謂可靠性反問題，可以看作是在指定可靠指標的前提下，求解極限狀態方程中影響結構的隨機變量統計參數，這些統計參數通常包括隨機變量的均值或標準差。

對于給定的目標可靠指標βT和極限狀態方程G（x）=0，X=（x1，x2，…，xn-1，ξ）是由若干個服從任意分布且相互獨立的隨機變量，U=（u1，u2，…，un-1，uξ）為通過當量正態化后的標準正態分布變量，其中ξ為待求的隨機變量。可靠性反問題可描述成為求解隨機變量ξ的參數（均值μξ或標準差σξ），使滿足：

用JC法進行可靠度分析時，可靠指標定義為標準正態空間內坐標原點到極限狀態曲面的最短距離，將極限狀態功能函數在U*（驗算點）進行Taylor級數展開，近似地取一階項，為：

驗算點u*的諸坐標表達式為：

其中，cosθui為法線OU*對坐標向量的方向余弦：

給定U和ξ的初始值U（0）和ξ0，設ξ為待求參數，將極限狀態方程在初值ξ0處進行Taylor展開，僅保留一次項：

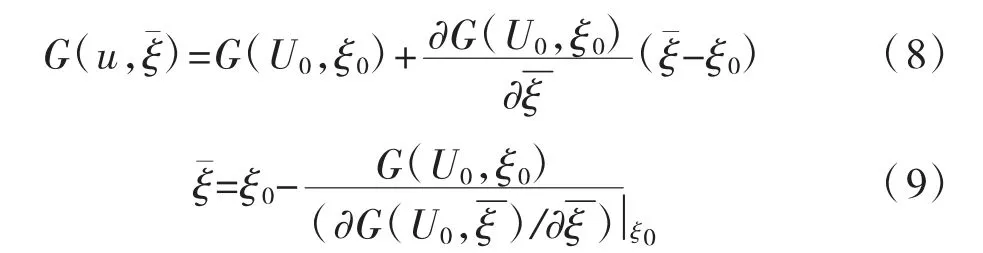
由上述公式求得一個新的向量U（i），同時滿足繼而得到新的ξ值，重復式（8）和式（9）的計算過程，直至U和ξ全部收斂。

參照可靠性反問題的求解方法，車輛限載取值的計算步驟總結如下：

（1）確定結構構件限載分析的抗力R和恒載效應SG的概率分布和統計參數、汽車效應SQ的概率分布類型、變異系數δQ與平均值系數KQ，并給定目標可靠指標βT；

（2）將抗力及荷載效應隨機變量進行當量正態化，轉換為標準正態空間下的隨機變量；

（3）在規定的作用效應組合下，建立極限狀態方程，按照上述單參數可靠性反問題的計算方法，求解出汽車效應平均值μQ；

（4）由公式SQ=μQ/KQ求得汽車效應標準值SQK，P，最后，根據SQK，P確定各限載車型的車重限值WP。

一般認為，車輛的軸重與總重保持一定的比例關系不變，即典型限載模型車輛的荷載效應與其車重成線性關系。基于這一假定，已知典型限載模型車輛的荷載效應SQ，即公路-I級荷載標準值效應，引入限載系數ξq=SQK，P/SQ，通行車輛的限載值WP按下式進行計算：

3.2 在役橋梁的車重限值分析方法

與在役橋梁評估相似，車輛限載分析應體現運營橋梁的“在役性”特征，即要體現橋梁的自身技術狀況，還需考慮管理者對橋梁的管養需求。管養需求一方面反映結構在運營中必須滿足的使用性能要求，同時又符合管理者對運營風險的承受能力，并受投資效益的制約。就安全和經濟兩方面而言，管養需求可表征為可靠指標的合理選取。

可靠指標的大小反映結構失效風險水平。在現行設計規范中，可靠指標一般在2.0~5.0范圍內進行取值，以滿足不同失效后果和安全措施成本的結構構件功能要求。就限載取值而言，可以預計，較大的可靠指標，使車輛的限載取值小，結構的運營風險減小，維護費用降低，線路運輸經濟效益降低；反之，車輛的限載取值大，雖增加經濟效益，但增加結構的失效概率、增加維護費用。

實際上，在役橋梁車輛限載主要是保證結構運營的安全性問題，因而，可靠指標取用可與結構設計或安全性評估要求相一致。對已運營一段時間的在役橋梁，根據自身結構的技術狀況，和特定的交通荷載環境，設置不同的目標可靠指標。因此，現建議：

對于技術狀況良好，且能滿足當前交通通行需求的橋梁，從結構耐久性和減少維護成本上考慮，宜維持設計的可靠指標。

對于技術狀況較差，不能滿足當前通行要求的橋梁，在保障運營安全前提下，適當降低結構使用要求，使運輸經濟效益最大化，建議在設計可靠指標上減1.0。

對于特定橋梁車輛限載分析步驟總結如下：

（1）確定限載分析的效應模式，如抗彎、抗剪等。

（2）在規定的作用效應組合下，建立極限狀態方程，并給定限載目標可靠指標βT。

（3）通過對結構的檢測和計算分析，確定結構在當前狀況下的承載力Rnd，抗力R和恒載效應SG的概率分布和統計參數，活載效應SQ的概率分布、變異系數δSQ與平均值系數KSQ。

（4）利用可靠性反問題的計算方法，求解出滿足目標可靠指標βT的活載效應平均值μSQ，由公式SQK=μSQ/KSQ求得汽車效應標準值SQK，最后，根據SQK確定各限載車型的車重限值WLV。

4 算例分析

某16 m鋼筋混凝土簡支T梁，橫向布置5片T梁，計算跨徑15.5 m，設計荷載等級為公路-I級。主梁采用C30混凝土，縱向主筋采用HRB335級鋼筋。橋梁的橫向斷面構造如圖3所示。

圖3 16 mT梁跨中橫斷面圖（單位：cm）

選擇跨中截面正彎矩為控制效應，抗力和效應的概率模型及參數可以根據檢測結果經計算得到，計算方法可參考相關文獻[8，9]，本文不再贅述。抗力和效應的概率模型和統計參數見表5所列。

分別按照設計要求的目標可靠指標βT=4.7和降低結構使用要求βT’=3.7進行限載。計算得到各片梁滿足限載可靠指標的汽車荷載效應標準值SQK，P，見表6所列。

從表6數據可以看出，邊梁T-1的狀況最為不利，根據設計汽車荷載效應標準值SQ（見表5），計算得到最小限載系數ξq分別為1.13和1.52，由此確定車型的車重限值見表7所列。對于六軸拖掛車，允許的最大車重分布為620 kN和835 kN。

表5 抗力和效應統計參數表

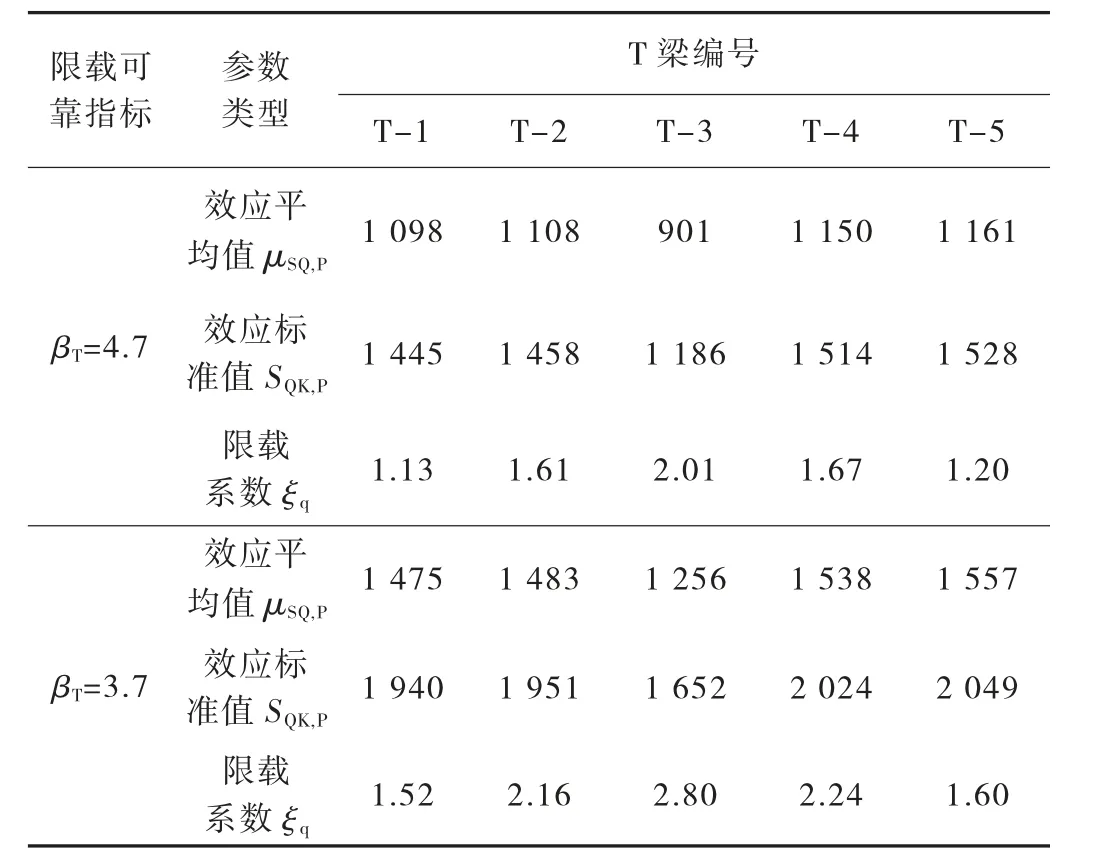
表6 限載汽車效應計算表

表7 16 m簡支T梁車重限值表

4 結論

從橋梁結構安全運營的角度，利用可靠度反問題的求解方法，提出了橋梁限載分析方法及限載車輛荷載模型。主要的研究結論如下：

（1）通過實測的車輛荷載數據統計，分析了載重車輛組成及車重與軸重分布特征。根據車型比例、車輛超載情況，以及軸組配置等因素對結構響應的影響，按軸型分類建立了橋梁限載分析的典型車型譜系。

（2）基于可靠度反問題的求解方法提出了橋梁限載分析方法，引入限載系數表示限載車重與設計汽車荷載之間的關系，并建立了在役橋梁安全運營的車輛限載分析步驟。

（3）通過算例，介紹了本文提出的在役橋梁限載分析的實施過程。結果表明，本文提出的車輛載重限值的取值方法能夠很好地體現結構可靠性思想，對橋梁限載決策的制定更具有科學的指導意義。