基于熵權聚類的國內空鐵綜合樞紐分類方法

嚴 琛，朱金福，馬睿馨，彭安娜

（南京航空航天大學民航學院，江蘇 南京 211106）

0 引言

交通樞紐是運輸網絡的重要節點，也是區域經濟發展的引擎。促進綜合交通樞紐發展能提高交通運輸整體效率、降低物流成本、方便廣大人民群眾出行。2017 年國務院《“十三五”現代綜合交通運輸體系發展規劃》（國發〔2017〕11號）[1]提出，優化綜合交通樞紐布局，完善集疏運條件，提升樞紐一體化服務功能；民用運輸機場應盡可能連接城際鐵路或市郊鐵路、高速鐵路，并同站建設城市公共交通設施。空鐵型綜合樞紐是將高鐵站點與機場合并，并與配套的其他交通方式站點設施融合和銜接形成的交通集散功能綜合體[2-3]。國外已有英國希斯羅綜合樞紐[2]、西班牙巴拉哈斯綜合樞紐的成功經驗[4]。國內大多數城市由于空鐵基礎設施規劃建設起步較晚，機場高鐵站數量較少，目前除上海虹橋[5]、北京大興等機場外，眾多機場與鐵路還未真正做到無縫銜接，旅客需通過其他地面交通方式接駁于機場與高鐵站之間。從發展的角度而言，機場方希望能有高鐵線路經過，以吸引周邊地區更多的客源。因此，需探索國內適宜發展成為空鐵綜合樞紐的城市，幫助城市機場向鐵路規劃部門爭取資源。

國外學者對綜合樞紐網絡的研究主要集中在空鐵競爭合作、多式聯運樞紐選址問題，在樞紐類別劃分方面研究較少。Givoni 等提出利用鐵路運輸作為航空樞紐網絡中的額外運力以補充和替代現有的網絡，而樞紐機場將從被釋放的時隙中獲益[2]。Socorro 等分別在機場容量限制、航司競爭緩和兩種情景下建立空鐵一體化合作模型，并從經濟理論角度評價其優點[6]。Meng 等建立多式聯運樞紐網絡模型，考慮運輸企業、樞紐運營商和多式聯運運營商等多方利益相關者[7]。Alumur等考慮多式聯運樞紐網絡的分層設計，并基于實際數據進行網絡構建[8]。國內有關綜合交通樞紐類別劃分的研究較多，主要采用的研究方法有層次分析法、主成分分析法、聚類法等。王文憲等采用近鄰傳播算法對國內日均旅客發送量排名前100 的鐵路客運節點進行聚類，引用三種聚類有效性指標對結果進行分析[9]。劉志萍等提出了綜合客運樞紐的分級分類方法和綜合客運樞紐分類規劃布局思路[10]。李萍等采用加權綜合理想解排序法及基于立方群準則的聚類法對京津冀城市群鐵路客運樞紐類別進行劃分[11]。朱倩等采用模糊聚類算法對我國西部地區城市多式聯運網絡樞紐進行分類，再結合國家政策調整類別[12]。有關空鐵綜合樞紐的鐵路和航空運輸組織如何有效銜接的文獻較少。孔明星根據旅客對時間、票價的需求差異，較為理想化地考慮票務一體化與全程服務性等要求，建立聯運網絡優化模型，設計最佳聯運路徑[13]。張祿采用案例分析法研究城市軌道交通對空鐵聯運的影響以及機場高鐵站對客流的吸引，分析空鐵聯運關鍵節點的選擇、基礎設施的統籌規劃、空鐵聯運產品的完善，指出空鐵信息互聯互通是未來的發展方向[14]。目前國內對空鐵綜合樞紐分類的研究較少，主要集中在特定區域或城市群內，缺少對全國大范圍的綜合考量，且對城市樞紐分類的影響因素考慮不全面。

本文考慮的空鐵綜合樞紐，是具備民航運輸能力以及鐵路運輸能力并且能實現兩種運輸方式有效換乘的綜合客運樞紐城市。從宏觀角度對國內332 個城市空鐵樞紐節點進行分類，建立樞紐類別的評價指標體系，采用熵值法賦權的Kmeans 聚類以及模糊C均值聚類算法，確定適宜發展空鐵聯運的全國性樞紐、區域性樞紐、地區性樞紐以及潛在地區性樞紐城市，以期為上述城市綜合客運樞紐站的規劃建設以及國內空鐵復合樞紐網絡構建提供依據。

1 空鐵綜合樞紐類別劃分依據

1.1 空鐵綜合樞紐類別劃分的指標選取

空鐵綜合樞紐是銜接航空運輸與鐵路運輸、輻射一定區域的客貨轉運中心。根據空鐵樞紐劃分的相關研究，以下指標均會對樞紐能力產生影響：交通基礎設施布局、樞紐線路連接數量、始發列車數量、客運量、所在城市的社會經濟發展水平等[15-16]。考慮數據的易獲取性以及各指標之間的替代關系，本文選擇以下三類因素對空鐵復合樞紐進行劃分。

（1）經濟屬性

城市經濟與當地交通運輸客運規模正相關，經濟繁榮會促進該地交通樞紐的形成與發展。選擇能反映城市經濟實力與產業結構的第二產業增加值（GDP2）、第三產業增加值（GDP3）作為樞紐類別劃分的指標。

（2）社會屬性

空鐵樞紐所在城市的人口數量、收入水平是影響樞紐等級的重要因素，城市人口基數越大，收入水平越高，則交通需求量越大，越有利于形成樞紐。因此選擇城市常住人口數量、人均可支配收入作為樞紐類別劃分的指標。

（3）交通屬性

成熟的空鐵綜合樞紐應當以航空運輸為主、鐵路運輸為輔，前者發揮中長距離運輸優勢，后者承擔短距離集疏運。研究表明線路數量、路網等級、旅客發送量等因素影響鐵路樞紐的類別；航線網絡、機場等級以及旅客吞吐量影響航空樞紐的類別。其中路網等級、機場等級難以量化，且鐵路運輸與航空運輸具有不同的特征，線路數量與航線網絡不具有可比性。為保證指標對稱性，選擇與客運量顯著相關的到發車次、航班架次作為樞紐類別劃分的指標，此外，選擇城市機場與火車站之間的換乘時間作為衡量空鐵銜接的指標。

1.2 指標量化分析

依據《中國城市年鑒》[17]以及各城市2018 年的《國民經濟和社會發展統計公報》獲取國內332 個城市（直轄市、地級市、自治州，不包含港澳臺地區）的第二產業增加值、第三產業增加值、常住人口數量、人均可支配收入數據；截取2018 年12 月31 日國內所有鐵路車站到發車次數據，所有機場的國內航班數據（擁有多座機場的城市作為一個節點，航班架次累積；少數機場考慮腹地范圍，如揚州泰州機場、西安咸陽機場、揭陽潮汕機場，將多座城市合并為一個節點，經濟數據累積）；根據高德地圖采集機場與火車站之間的換乘時間數據，若某城市有機場高鐵站則該項數據為0，若該城市無機場/無火車站則按時間最短匹配到附近城市相應基礎設施。部分數據如表1所示。

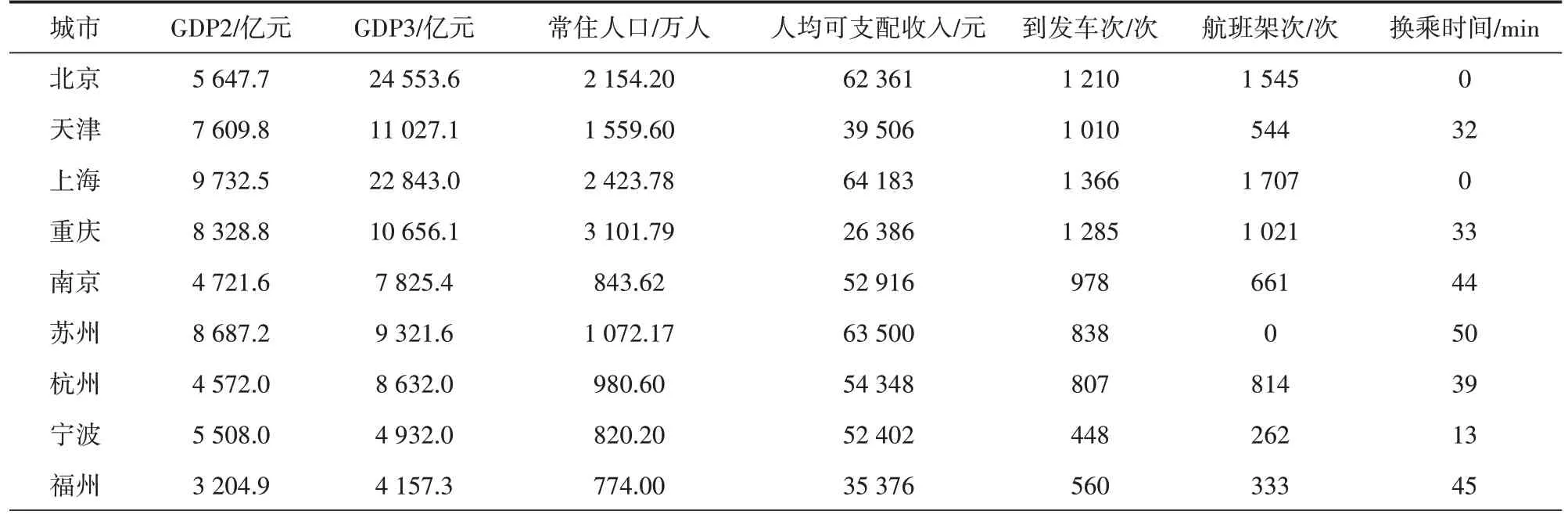
表1 空鐵綜合樞紐類別劃分指標數據（部分城市）

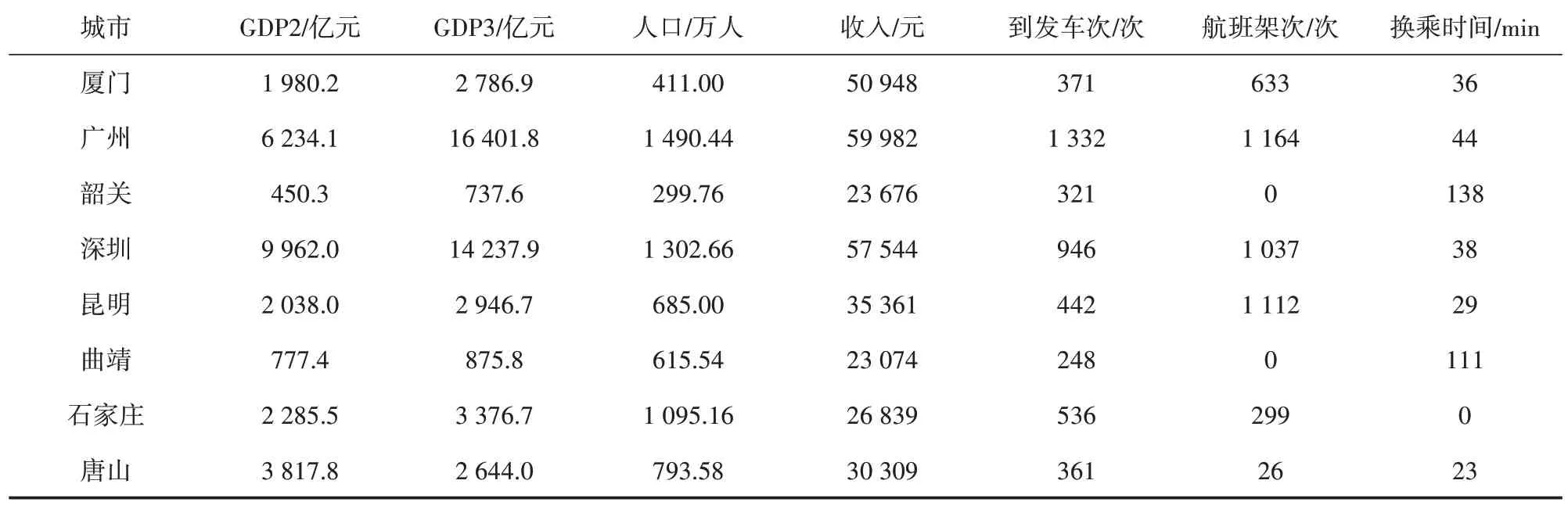
表1（續）

1.3 指標權重確定

為保證評價的客觀性，選擇熵值法為指標賦權。在信息論中，熵是對不確定性的一種度量，信息量越大，不確定性就越小，熵也就越小。根據熵的特性，可以通過計算熵值來判斷某個指標的離散程度，指標的離散程度越大，該指標對綜合評價的影響（權重）越大。計算步驟如下：

（1）所有指標歸一化處理

前六項指標為正向指標，對于m行n列正向指標的原始數據集X={xij}m×n進行離差標準化：

若某個元素標準化后為0，則替換為極小數1× 10-6，避免取自然對數時出現無意義情況。

（2）計算第j項指標下第i個元素占該項指標的比例pij

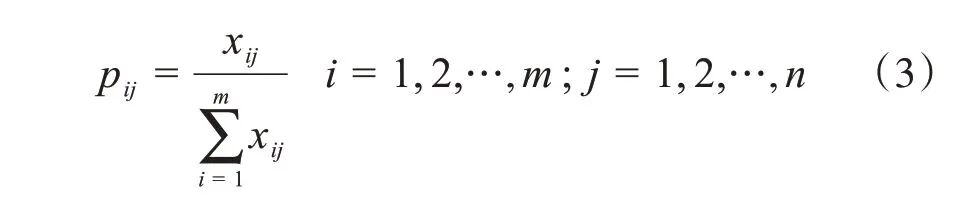
（3）計算第j項指標的熵值ej

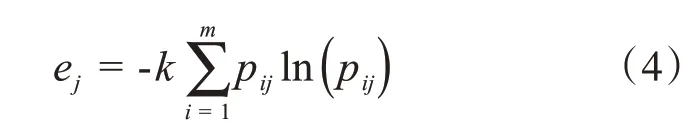
其中k=1/ln(n)＞0，滿足ej≥0。

（4）計算冗余度dj

（5）計算指標權重wj

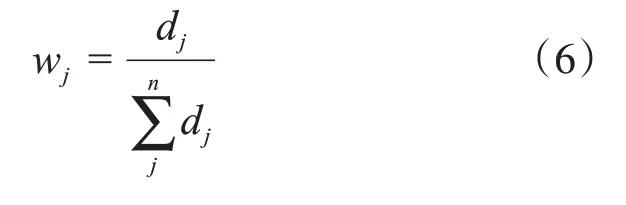
由上述步驟計算出權重向量為：

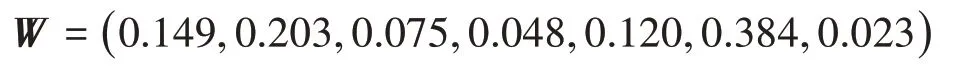
綜上可知航班架次為空鐵樞紐評價的關鍵指標，與以航空運輸為主、鐵路運輸為輔的預期較為符合。

2 基于K-means 聚類的空鐵綜合樞紐類別劃分

2.1 K-means聚類算法原理

聚類是一個將數據集中在某些方面相似的數據成員進行分類組織的過程。K-means 聚類算法具有簡潔高效性，其被廣泛應用于統計學、生物學、市場營銷學等各個領域。

K-means算法步驟如下：

（1）對于樣本集X隨機抽取k個初始中心點；

（2）對于每個樣本點，計算到這k個中心點的歐式距離，將樣本點歸到與之距離最小的那個中心點所在類；

（3）對于每個類，根據其所有樣本點重新計算得到一個新的中心點，如果中心點發生變化則返回步驟（2），若中心點未發生變化則算法停止。

K-means 需要事先知道類別數目，而如何確定最佳的分類仍是聚類分析中尚未完全解決的問題之一。在實際應用中則主要根據研究目的，從使用的角度選擇合適的分類數。

2.2 K-means聚類結果

將原始數據0-1 標準化處理，再將指標數據乘以權重W得到樣本集X。在SPSS 軟件上運行K-means 聚類，最大迭代次數設置為20。研究預先將數據集聚為4～6 類進行測試，按照“類別劃分合理且具有解釋意義”的原則，最終選擇k=5。按照關鍵指標6（航班架次）為類別排序。聚類中心見表2，聚類劃分結果見表3。

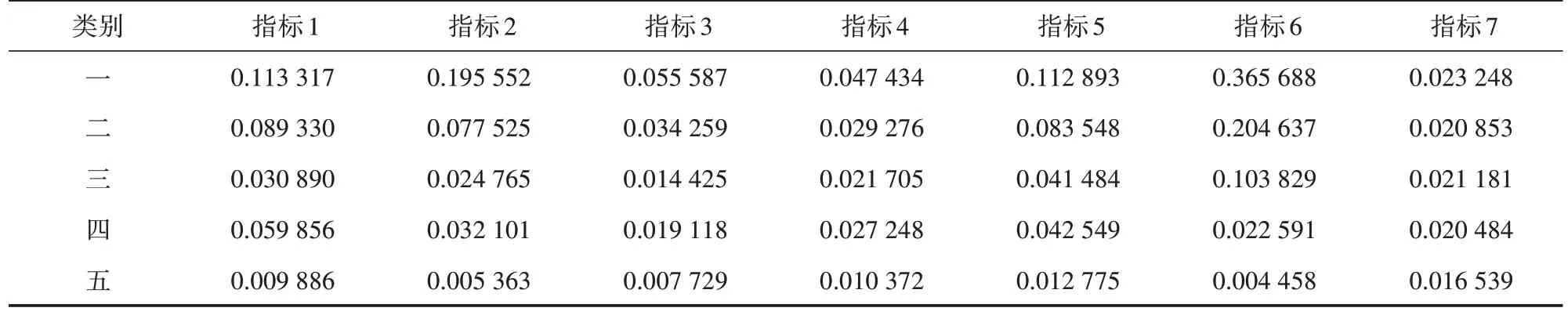
表2 K-means聚類中心

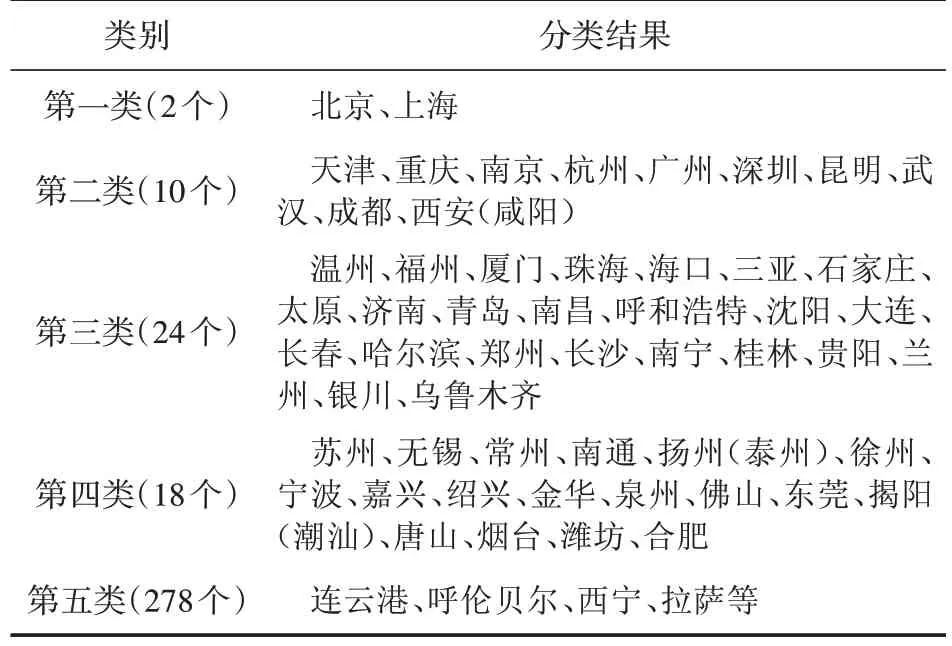
表3 K-means聚類結果

3 基于模糊C 均值聚類的空鐵綜合樞紐類別劃分

3.1 模糊C均值聚類算法原理

模糊聚類分析一般指根據研究對象本身的屬性來構造模糊矩陣，并在此基礎上根據一定的隸屬度來確定聚類關系，即用模糊數學的方法把樣本之間的模糊關系定量，從而客觀且準確地進行聚類，其中模糊C均值聚類（Fuzzy C Means,FCM）應 用 最 為 廣 泛[17]。FCM 把n個 向 量xi(i=1,2,…,n)分為C個模糊組，并求每組的聚類中心，使得非相似性指標的價值函數達到最小。

FCM的目標函數如下：

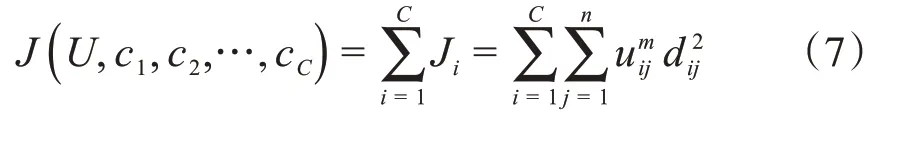
其中uij∈[0,1]，ci為模糊組i的聚類中心，dij=‖ci-xj‖為第i個聚類中心與第j個數據點間的歐式距離；m為模糊系數也稱為平滑參數，一般取2。

令J對ci和uij偏導等于0，求得極小值的必要條件：

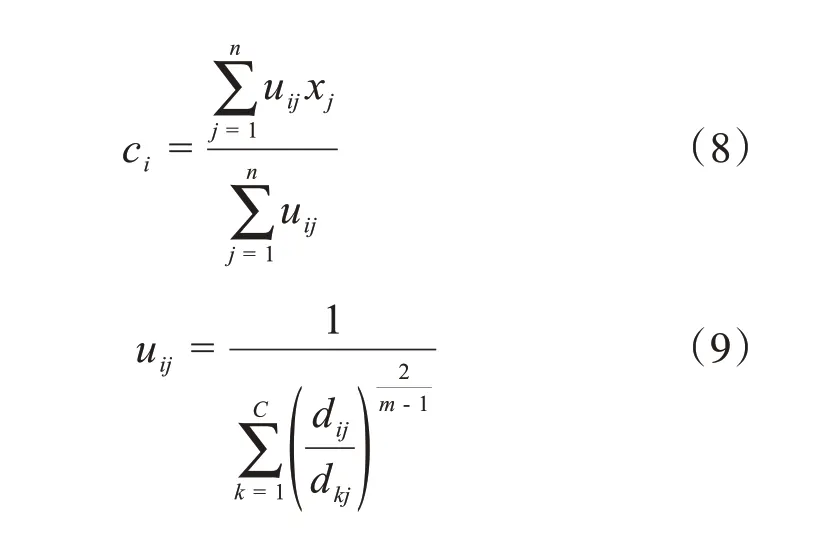
由式（8）、式（9）可知，FCM 聚類是一個迭代過程，算法步驟如下：

（1）生成(0,1)之間的隨機數初始化隸屬矩陣U。

（2）用式（2）計算C個聚類中心ci，i=1,2,…,C。

（3）計算價值函數J，若其小于某個閾值，或相對上次價值函數值的改變量小于某個閾值，則算法停止。

（4）用式（3）計算新的矩陣U，返回步驟（2）。

3.2 模糊C均值聚類結果

在Matlab 中按上述算法步驟編寫FCM 程序，輸入樣本集X，設置類別個數C=5，模糊系數m=2，收斂精度為1× 10-6，可得到隸屬度矩陣以及聚類中心。按關鍵指標6（航班架次）為類別排序。為進一步研究需要，將城市節點劃分至其隸屬度最大的類別中，聚類隸屬度矩陣見圖1，聚類中心見表4，聚類劃分結果見表5。

圖1 FCM隸屬度矩陣圖

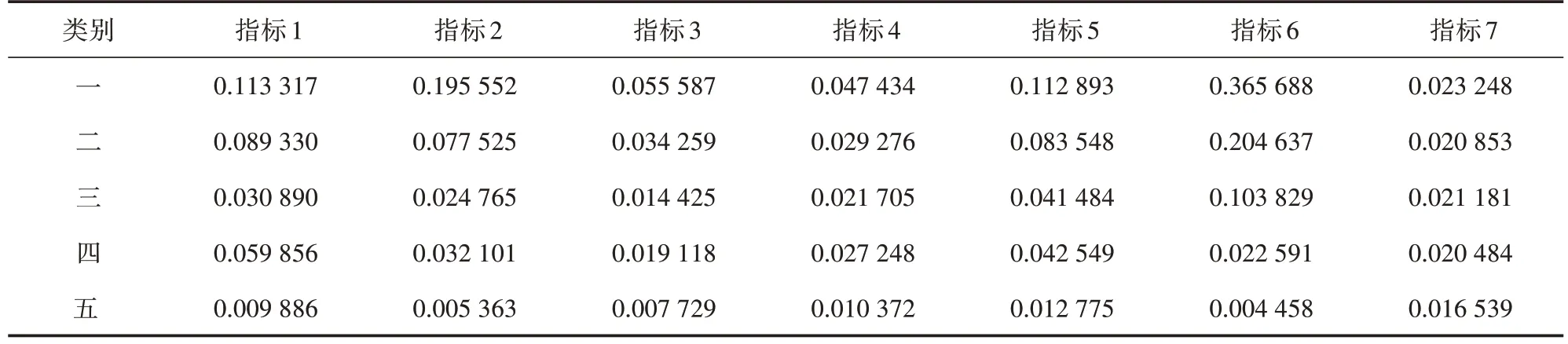
表4 FCM聚類中心

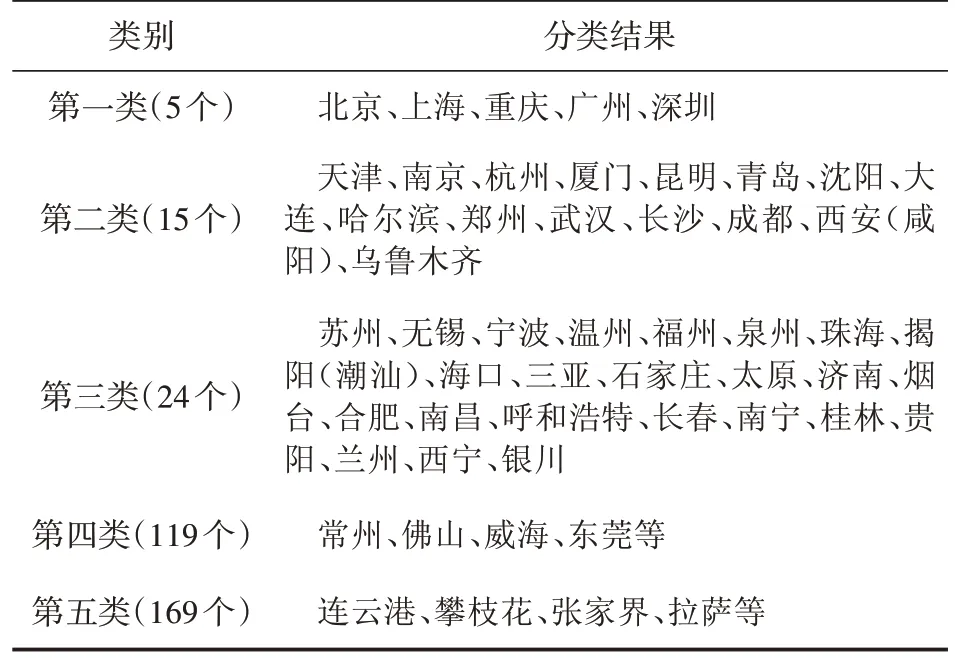
表5 FCM聚類結果

4 比較分析

將類別1～5 分別命名為全國性樞紐、區域性樞紐、地區性樞紐、潛在地區樞紐、一般地方節點。總體而言，在樞紐類別劃分中靠前的城市，可作為發展空鐵聯運的重要試點城市，若原有機場與高鐵站并不重合，則可通過建設機場高鐵站/城鐵站將原有機場與鐵路有機銜接起來，成為無縫銜接的空鐵綜合樞紐；在樞紐類別劃分中靠后的城市在國內空鐵聯運網絡中起輔助作用，可為臨近的高級樞紐服務。兩種算法的分類結果有相似之處，但存在差異。K-means 聚類結果較為嚴格，每類占比分別為0.60%,3.01%,7.23%,5.42%,83.73%，前四類較低，第五類較高；聚類中心第四類的社會經濟指標均顯著優于第三類，鐵路指標以及銜接指標數值相近，只有關鍵指標航班架次低于第三類，揭示出第四類城市（大多數為東南沿海城市）的民航運輸能力還有待提高，以匹配當地社會經濟的發展。FCM 聚類結果呈現明顯的金字塔結構，每類占比分別為1.51%,4.52%,7.23%,35.84%,50.90%；前三類占比較低，第四類和第五類占比較高；聚類中心分層排列，高級別的樞紐每項指標均優于低級別的樞紐。

就區域而言，兩種分類結果均呈現出東南沿海地區城市樞紐等級較高，密度較大，中西部地區城市樞紐等級較低，且較為分散的特點，與國內目前東西部經濟發展不平衡的客觀實際以及人口空間分布特征相符。此外，京津冀、長三角、珠三角城市群中地區性樞紐—區域性樞紐—全國性樞紐層層遞進，表明這些地區適宜優先建設空鐵復合樞紐，作為發展空鐵聯運的先驅。較為成功的案例已有上海虹橋綜合交通樞紐和北京大興綜合交通樞紐，仍在規劃中的廣深第二高鐵將連接廣州白云機場與深圳寶安機場，助力廣深空鐵復合樞紐形成。

就城市而言，北京、上海在兩種分類下都為第一類，符合國家總體規劃。K-means 聚類結果中省會城市合肥被分至第四類，原因為合肥新橋國際機場與南京祿口國際機場在客源腹地方面的競爭中處于劣勢；而西寧、拉薩被分至第五類，除去經濟基礎原因，西寧曹家堡機場（2 178m.a.s.l.）為高原機場，拉薩貢嘎機場為高高原機場（3 570m.a.s.l.），飛行條件存在諸多困難，且目前鐵路運輸能力較差，可見兩市不適宜發展為空鐵綜合樞紐。在第四類中的蘇州、東莞兩市截至目前尚沒有運輸機場。雖然蘇南碩放機場距離蘇州市中心僅37km，但由于該機場性質為軍民合用，發展受到極大限制，無法滿足市民的出行需求，客流被分至上海虹橋國際機場（距離約為89km）、上海浦東國際機場（距離約為142km）。東莞市中心與廣州白云國際機場及深圳寶安國際機場距離相當，分別為83km、65km，且市內有兩座機場的城市候機樓，客流同樣被分攤。蘇州、東莞兩市的經濟實力在全國范圍內名列前茅，大量人口帶來旺盛的交通需求，而樞紐發展離不開社會經濟的有力支撐，聚類結果表明這兩個城市具有成為區域性樞紐的潛質，或者成為空鐵聯運的服務對象，配套的基礎設施應該納入規劃建設中。FCM 聚類結果中大多數省會城市在第二類和第三類，拉薩同樣被分至第五類，原因不再贅述。與K-means 聚類結果相比，FCM 聚類結果放寬了第一類與第二類的條件，即能成為區域性樞紐及全國性樞紐的城市節點明顯增多，且提高了重慶、廣州、深圳、烏魯木齊等城市的樞紐評級，更具有發展性。兩種聚類結果中海口都在第三類，與《國家綜合立體交通網規劃綱要》中所提的“國際性綜合交通樞紐城市”相比，定位偏低，原因如下：目前海口與內陸還未通高鐵，跨海大通道湛海高鐵仍在規劃中，短期內無法成為國內空鐵綜合樞紐，但作為海南自由貿易港核心城市，政策優勢使其具有發展成為亞太航空樞紐的潛質。

綜上所述，單個城市節點雖受制于其社會經濟發展水平、地理環境等，但總體上其所屬樞紐類別仍較為準確。由于K-means 聚類和模糊C均值聚類都屬于機器學習分類下的無監督學習，缺乏足夠的先驗知識，同一樣本集使用兩種聚類算法的分類結果不一樣，但各自有適用條件，分別在現實性和前瞻性的角度上合理。因此本文只提供兩種算法的分類結果，為城市空鐵綜合樞紐規劃建設提供一定依據和評判標準。

5 結語

本文以國內332 個城市為研究對象，建立空鐵綜合樞紐能力評價指標體系，通過較客觀的熵值法加權的K-means 聚類以及模糊C均值聚類兩種算法，對國內城市的空鐵綜合樞紐能力進行分類，提出5 個樞紐類別。從區域和城市的角度比較分析了兩種聚類的結果，K-means 聚類結果較為嚴格，模糊C均值聚類結果更能識別出潛在樞紐。樞紐類別劃分結果有利于國內綜合交通樞紐的規劃與建設，對城市交通發展具有參考意義；在民航與高鐵競合博弈的背景下可為航空公司選擇樞紐基地、構建樞紐航線網絡提供支撐。未來民航與高鐵在國內運輸市場結合各自運力優勢構建空鐵聯運網絡，離不開空鐵綜合樞紐基礎設施的建設發展以及空鐵聯運產品的設計和完善，如何達成合作共贏值得深入研究。