EQ-代數上的核算子

梁 婕， 王軍濤

（1.陜西鐵路工程職業技術學院 基礎課部，陜西 渭南714000； 2.西安石油大學 理學院，陜西 西安710065）

1 序言

核算子的概念在拓撲學中起著十分重要的作用［1-3］.文獻［1］說明了在frame上的frame映射就其本身而論就是完備的Heyting代數上的核算子.而從邏輯角度來看，核算子作為直覺主義命題邏輯的代數配對物，目前已經在多種邏輯代數中被廣泛的研究.

1981年，Macnab［4］證明了在Heyting代數上核算子的一些性質；受到Macnab思想的啟發，文獻［5］介紹了MV-代數上的核算子，文獻［6］介紹了BCI-代數上的微分，文獻［7］介紹了格上固定點集的微分，文獻［8］介紹了EQ-代數上的核算子等等.特別地，2011年，Kondo［9］介紹了有界的交換單位剩余格（CRL），在不滿足可分性（x∧y＝x⊙（x→y））的情況下單調的核算子和核算子是不相同的.而EQ-代數是較它們而言更為一般的代數結構.基于此，研究EQ-代數上的核算子是有意義的.本文討論EQ-代數上的核算子，主要內容如下：

1）給出剩余EQ-代數E上的單調核算子與強核算子的等價刻畫.證明在單調核算子f下，E的像f（E）是一個剩余EQ-代數；

2）研究剩余EQ-代數E上的3類特殊的映射，討論3類特殊的映射與強核算子之間的關系.

2 預備知識

定義2.1［10-11］一個（2，2，2，0）型的代數（E，∧，⊙，～，1）滿足以下條件，對任意的a，b，c，d∈E，有：

（E1）（E，∧，1）是一個有著最大元1的∧-半格；

（E2）（E，⊙，1）是一個含幺半群，且對⊙雙邊保序；

（E3）a～a＝1（自反公理）；

（E4）（（a∧b）～c）⊙（d～a）≤c～（d∧b）（替換公理）；

（E5）（a～b）⊙（c～d）≤（a～c）～（b～d）（同余公理）；

（E6）（a∧b∧c）～a≤（a∧b）～a（單調公理）；

（E7）a⊙b≤a～b（有界公理）；則稱（E，∧，⊙，～，1）是一個EQ-代數.

二元運算∧、⊙和～分別被稱為交、乘和模糊相等，并且規定對任意的a，b∈E，有

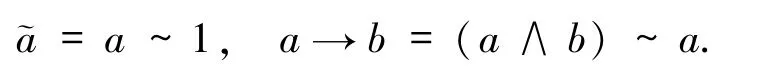
由于（E，≤）是一個偏序集，則a≤b當且僅當a∧b＝a.在本文中，如果EQ-代數對⊙交換，則稱它為可交換的EQ-代數.

下面的EQ-代數（E，∧，⊙，～ ，1）簡記為E.

定義2.2［10］設E為一個EQ-代數，則稱它為：

1）好的，如果對任意的a∈E，有a~＝a；

2）剩余的，如果對任意的a，b，c∈E，（a⊙b）∧c＝a⊙b當且僅當a∧（（b∧c）～b）＝a；

3）對合的，如果對任意的a∈E，有a－－＝a.

命題2.3［10-12］設E為一個EQ-代數，則對任意的a，b，c∈E，下列性質成立：

1）a～b＝b～a（對稱性）；

2）（a～b）⊙（b～c）≤a～c，（傳遞性）；

3）a～b≤a→b和a→a＝1；

4）（a→b）⊙（b→c）≤a→c和（b→c）⊙（a→b）≤a→c；

5）若a≤b，則a→b＝1；

6）a⊙b≤b≤b~≤a→b；

7）a⊙（a～b）≤b~；

8）a⊙b≤a，a⊙b≤a∧b，c⊙（a∧b）＝（c⊙a）∧（c⊙b）；

9）若a≤b→c（a≤b～c），則a⊙b≤c~；

10）若a≤b，則c→a≤c→b和b→c≤a→c.

如果E是剩余的，則：

11）a⊙（a→b）≤b，

12）a→（b→c）＝（a⊙b）→c＝b→（a→c），

13）a⊙（b→c）≤b→（a⊙c）≤（a⊙b）→（a⊙c）.

定理2.4［10］設E是一個好的EQ-代數，則下面的式子成立，對任意的x，y，z∈E，有：

1）x≤（x→y）→y，

2）x→（y→z）＝y→（x→z）.

引理2.5［10］設E為一個EQ-代數，則下面的表述是等價的：

1）E是剩余的；

2）E是好的并且對任意的a，b∈E，有a≤b→（a⊙b）成立.

3 核算子的定義和性質

文獻［8］研究了Quantale代數中的核映射，并用以刻畫Quantale的代數結構.而EQ-代數作為高階模糊邏輯的真值代數結構，不僅為模糊型理論提供了更為廣泛的真值代數結構，而且是剩余格的一般化.基于此，本節將介紹EQ-代數上的核算子，并討論一系列的性質.

定義3.1設E是一個EQ-代數，則一元映射f：E→E被稱為是E上的核算子.如果對任意的x，y∈E，f滿足下面的條件：

1）x≤f（x），

2）f（f（x））＝f（x），

3）f（x⊙y）＝f（x）⊙f（y）.

一個二元運算⊕通過x⊕y＝（x－⊙y－）－被定義，其中x－＝x→0.規定：除了特別說明外，對任意的x∈E，本文中的x－＝x→0.

下面給出一個EQ-代數上核算子的例子.

例3.2設E＝｛0，a，b，1｝且0＜a＜b＜1，其中⊙和～按照如下方式定義：

則（E，∧，⊙，～，1）是一個EQ-代數［13］.現在按照如下方式定義一個映射f：E→E：

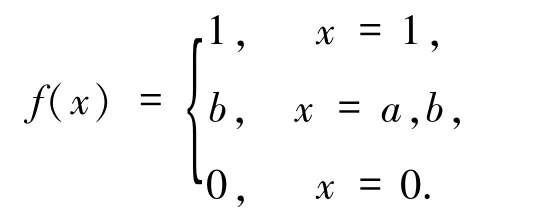
容易驗證f是E上的一個核算子.

設f是一個核算子，對任意的x，y∈E滿足x≤y，有f（x）≤f（y），則f是單調的.

下面的例子是為了說明不是所有的核算子都是單調的.

例3.3設E＝ ｛0，a，b，c，d，1｝，其中0＜a，b＜c＜d＜1，a與b不可比較（即a與b沒有序關系）.運算⊙和～定義如下：

則（E，∧，⊙，～，1）為一個EQ-代數.定義映射f：E→E如下：

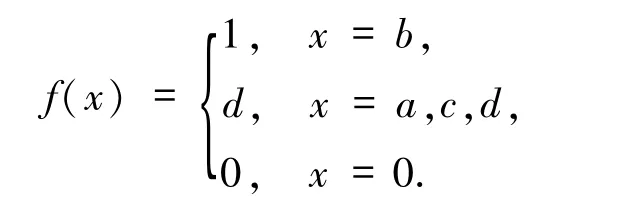
容易驗證f是一個核算子.然而f不是單調的，因為b＜c，但是1＝f（b）≤／f（c）＝d.

注1文獻［14］證明了剩余EQ-代數是剩余格的一般化，而文獻［9］中剩余格上的modal算子事實上可看成一種核算子.以下將著重討論剩余EQ-代數上的核算子及其性質，并依此研究核算子下象的代數結構.

命題3.4設E是一個EQ-代數，并且f是E上的一個單調核算子.對任意的x，y∈E，則下面的式子成立：

1）如果E是剩余的，則f（x→y）≤f（x）→f（y）＝f（f（x）→f（y））＝x→f（y）＝f（x→f（y））；

2）如果E是剩余的，則f（x）≤（x→f（0））→0；

3）如果E是剩余的，則f（x）⊙x－≤f（0）；

4）如果E是剩余的，則f（x）≤f（x－－）≤x⊕f（0）；

5）f（x）∧f（y）＝f（f（x）∧f（y））.

證明1）對任意的x，y∈E，由x⊙（x→y）≤y推出f（x⊙（x→y））≤f（y）.根據f是一個核算子，則有f（x）⊙f（x→y）≤f（y），這就意味著f（x→y）≤f（x）→f（y）.由于x≤f（x），則根據命題2.3的10）可得f（x）→f（y）≤x→f（y）.因此，f（x）→f（y）≤x→f（y）≤f（x→f（y））≤f（x）→f（f（y））＝f（x）→f（y），即f（x）→f（y）≤f（f（x）→f（y））≤f（f（x））→f（f（y））＝f（x）→f（y）.所以，f（x→y）≤f（x）→f（y）＝f（f（x）→f（y））＝x→f（y）＝f（x→f（y））.

2）由陳述1）可得f（x）→f（0）＝x→f（0），并且由f（x）⊙（f（x）→f（0））≤f（0）可以得到f（x）≤（f（x）→f（0））→f（0）＝ （x→f（0））→f（0）.

3）由陳述1）有x→0≤f（x→0）≤f（x）→f（0），也就是說，f（x）⊙x－≤f（0）.

4）由定理2.4的1），有x≤（x→y）→y，令y＝0可得x≤x－－.由f是單調的，容易得到f（x）≤f（x－－）.由陳述3）知道

f（（x→0）→0）⊙（（（x→0）→0）→0）≤f（0）.

因此，有

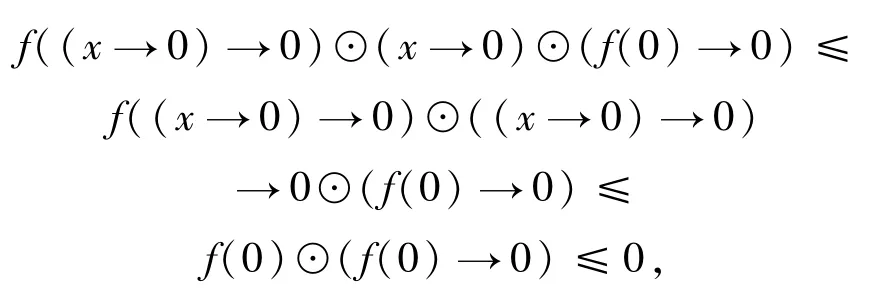
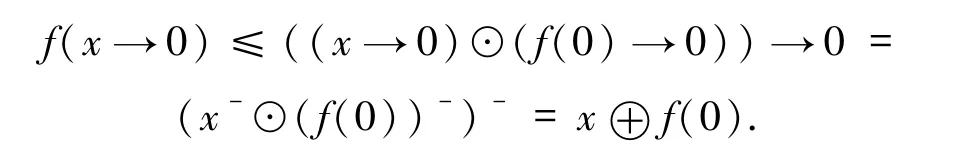
即

5）因為f（x）∧f（y）≤f（x），f（y），因此f（f（x）∧f（y））≤f（f（x）），f（f（y）），即f（f（x）∧f（y））≤f（x）∧f（y）.反過來，因為f是單調的核算子，則f（x）∧f（y）≤f（f（x）∧f（y））.也就是說，f（x）∧f（y）＝f（f（x）∧f（y））.

一個單調的核算子f如果滿足對任意的x，y∈E，f（x⊕y）＝f（x⊕f（y）），則f為強核算子.

命題3.5設E是一個剩余的EQ-代數，f是E上的單調核算子，并且滿足對任意的x∈E，有x⊕f（0）＝f（x⊕0）成立，則f（x）⊕f（0）＝x⊕f（0）.

證明由命題3.4的4）知f（x）≤x⊕f（0），又由于

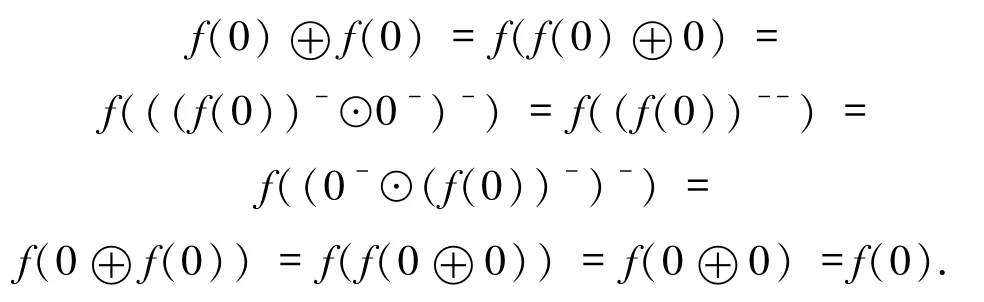
因此，f（x）⊕f（0）≤x⊕f（0）⊕f（0）＝x⊕f（0）.

反過 來，由x≤f（x）可 得 （f（x））－⊙（f（0））－≤x－⊙（f（0））－，由命題2.3的10）有（x－⊙（f（0））－）－≤（（f（x））－⊙（f（0））－）－，也就是說，f（x）⊕f（0）≥x⊕f（0）.

綜上所述，f（x）⊕f（0）＝x⊕f（0）.

命題3.6設E是一個剩余EQ-代數，并且f是E上的單調核算子，則f是強核算子當且僅當f滿足對任意的x∈E，x⊕f（0）＝f（x⊕0）成立.

證明假設f是強核算子，由命題3.4的4）可得f（x⊕0）＝f（（x－⊙0－）－）＝f（x－－）≤x⊕f（0）.由f是核算子有x⊕f（0）≤f（x⊕f（0））＝f（x⊕0）.因此，可得x⊕f（0）＝f（x⊕0）.

反過來，假設x⊕f（0）＝f（x⊕0）.由對任意的x，y∈E，有

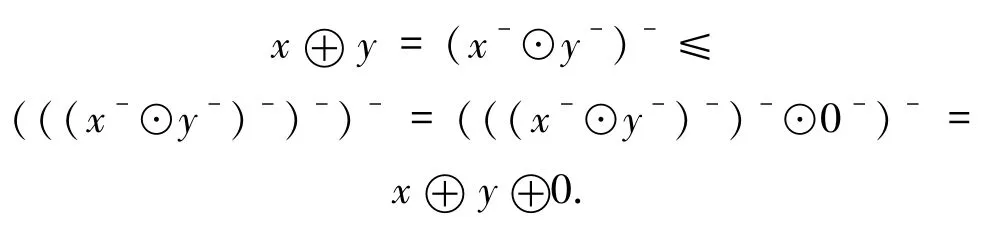
由命題3.5可得

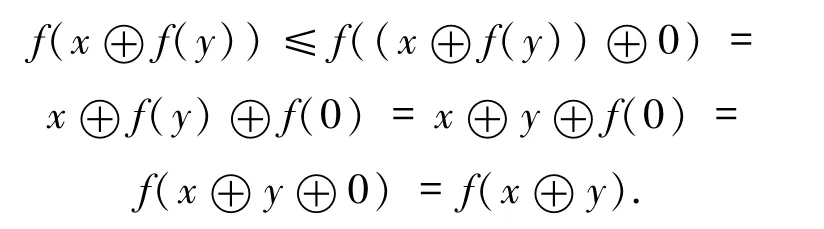
故有f（x⊕f（y））≤f（x⊕y）.另一方面，由y≤f（y），可得x－⊙（f（y））－≤x－⊙y－，也就是說（x－⊙y－）－≤（x－⊙（f（y））－）－.因此，由f是單調的可知f（x⊕y）≤f（x⊕f（y））.通過以上分析可得f是強核算子.

定理3.7設E是一個剩余EQ-代數，則f是E上的單調核算子當且僅當f滿足下面的條件，對任意的x，y∈E，有：

（a）f（x）→f（y）＝x→f（y），

（b）f（x⊙y）≤f（x）⊙f（y）.

證明由命題3.4的1）和f是E上的單調核算子易知f滿足上面的條件.

反過來，即要證明如果f滿足條件（a）和（b），則f是一個單調的強核算子.

由（a）可得1＝f（x）→f（x）＝x→f（x），有x≤f（x）.

如果x≤y≤f（y），則可得1＝x→f（y）＝f（x）→f（y），這就意味著f（x）≤f（y）.也就是說，f是一個保序映射.

由（a）可以推導出1＝f（x）→f（x）＝f（f（x））→f（x），由前面證明知f（x）≤f（f（x）），所以有f（x）＝f（f（x））.

最后要證明f（x⊙y）≤f（x）⊙f（y）.因為x⊙y≤f（x⊙y），可得y≤x→f（x⊙y）＝f（x）→f（x⊙y）.因此，f（x）≤y→f（x⊙y）＝f（y）→f（x⊙y）.也就是說，f（x⊙y）≥f（x）⊙f（y）.又由條件（b）知f（x⊙y）≤f（x）⊙f（y）.通過以上分析，可以總結出f是E上的單調核算子.

推論3.8設E是一個剩余的EQ-代數.則f是E上的強核算子當且僅當f滿足下面的條件：對任意的x，y∈E，有：

（a）f（x）→f（y）＝x→f（y）；

（b）f（x⊙y）≤f（x）⊙f（y）；

（c）x⊕f（0）＝f（x⊕0）.

定理3.9設E是一個剩余EQ-代數，f是E上的單調核算子，并且f在E中的像f（E）滿足f（x～y）≤f（x）～f（y），則（f（E），∧，⊙，～1，1′）也是一個剩余EQ-代數.在這里，對任意的x，y∈E，x～1y＝f（x～y），1′＝f（1）.

證明首先，由命題3.4的1）和5）可得f（E）對于運算→和∧封閉.根據f是單調的，對任意的x∈f（E），若x≤1，可得f（x）≤f（1），即1′是f（E）的最大元.因此，（f（E），∧1，1′）是一個有著最大元1′的∧-半格.

現證（E，⊙，1′）是一個交換群.由f是E上的核算子知道f（E）對于運算⊙封閉，并且對任意的f（x）∈f（E）有

對任意的a，b，c，d∈f（E），有（（a∧b）～c）⊙（d～a）≤c～（d∧b）.又由于f是核算子，有

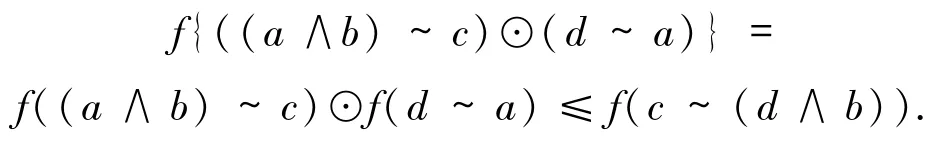
也就是說（（a∧b）～1c）⊙（d～1a）≤c～1（d∧b）.類似地，可以證明（a∧b∧c）～1a≤（a∧b）～1a.

對任意的a，b，c，d∈f（E），有 （a～b）⊙（c～d）≤（a～c）～（b～d）成立.由于又f是核算子，可以得到

和

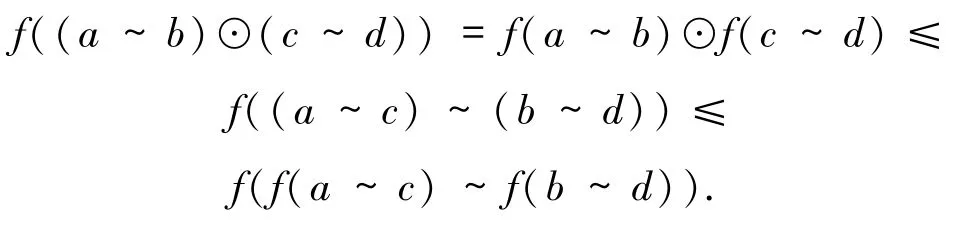
因此，（a～1b）⊙（c～1d）≤（a～1c）～1（b～1d）.

對任意的a，b∈f（E），有a⊙b≤a～b成立.而根據f是單調的可以得到a⊙b≤f（a⊙b）≤f（a～b）＝a～1b.

對任意的a∈f（E），得到a～1a＝f（a～a）＝f（1）＝1′.

最后證明f（E）滿足伽羅瓦連接.對任意的f（x），f（y），f（z）∈f（E），由于x⊙y≤z，推出x≤y→z，由命題3.4可得f（x）⊙f（y）＝f（x⊙y）≤f（z），推出f（x）≤f（y→z）≤f（y）→f（z）.另一方面，由f（x）≤f（y）→f（z）有

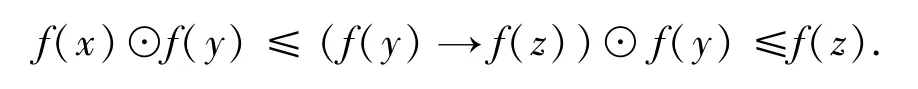
因此，可得（f（E），∧，⊙，～1，1′）是一個剩余EQ-代數.

推論3.10設E是一個剩余EQ-代數并且f是E上的單調核算子，則f（0）＝0當且僅當f（x）≤x－－，?x∈E.

證明假設f（0）＝0，由命題3.4的2）知f（x）≤（x→f（0））→f（0）＝ （x→0）→0＝x－－.因此，f（x）≤x－－.

反過來，如果f（x）≤x－－，則令x＝0可得f（0）≤x－－＝0.由x≤f（x），對任意的x∈E，可得0≤f（0）.

推論3.11設E是一個剩余EQ-代數，f是E上的核算子并且?x∈E使得f（x）＝x，則對任意的x，y∈E，可得x→y－＝f（x）→（f（y））－.

證明由于（x⊙y）⊙（（x⊙y）→0）≤0，可得（f（x）⊙f（y））⊙（（x⊙y）→0）≤0，根據命題2.3的12）有（x⊙y）→0≤f（x）→（f（y）→0），即x→（y→0）≤f（x）→（f（y）→0），也就是說x→y－≤f（x）→（f（y））－.同理可得f（x）→（f（y））－≤x→y－.因此，x→y－＝f（x）→（f（y））－.

下面將討論對合剩余EQ-代數.

定理3.12設E是一個對合剩余EQ-代數，則－－是強核算子.

證明假設E是一個對合剩余EQ-代數，容易證明：

1）x≤x－－；

2）如果x≤y，則x－－≤y－－；

3）由命題2.5可得x≤x－－，即x－－－－≤x－－，又 由 假 設 有x－－≤x－－－－，因 此，x－－－－＝x－－；

4）（x⊙y）－－＝x⊙y＝x－－⊙y－－.

這就意味著運算－－是一個單調的核算子.進一步，因為

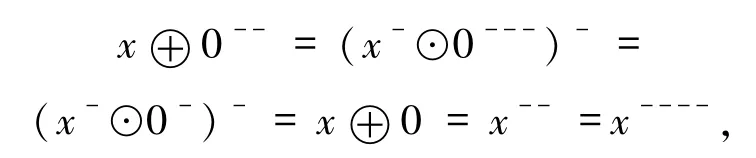
也就是說，－－是強核算子.

命題3.13設E是一個對合剩余EQ-代數，則a－∈B（E）當且僅當a⊕a＝a－－.

證明如果a－∈B（E），則可得a⊕a＝（a－⊙a－）－＝（a－）－＝a－－.

反過來，如果a⊕a＝a－－，則a－＝a－－－＝（a⊕a）－＝a－⊙a－，可得a－∈B（E）.

設E是一個剩余EQ-代數，則映射φa：E→E表示對任意的a，x∈E，有 φa（x）＝a⊕x.

推論3.14設E是一個對合剩余EQ-代數.則對任意的x，y∈E，a⊕（x⊕y）＝（a⊕x）⊕（a⊕y）＝a⊕（x⊕（a⊕y））當且僅當a－∈B（E）.也就是說，φa（x⊕y）＝φa（x⊕φa（y））當且僅當a－∈B（E）.

證明假設對任意的x，y∈E，a⊕（x⊕y）＝（a⊕x）⊕（a⊕y）.令x＝y＝0，則可得a⊕（0⊕0）＝（a⊕0）⊕（a⊕0），由于a⊕0＝（a－⊙0－）－＝a－－和0⊕0＝（0－⊙0－）－＝0，故

a－－＝a－－⊕a－－＝（a－－－⊙a－－－）－＝a⊕a.根據命題3.13可得a－∈B（E）.

反過來，如果a－∈B（E），因為a⊕a＝a－－，則

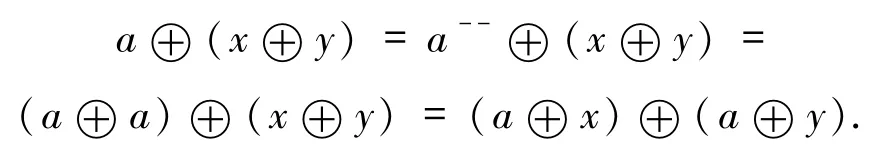
4 剩余EQ-代數上其他算子的研究

為了更好地刻畫出單調核算子以及強核算子，本節將重點研究3類特殊算子的性質：φa（x）＝a⊕x，ψa（x）＝a→x和 χa（x）＝（x→a）→a，對于a∈E.

引理4.1設E是一個對合剩余EQ-代數，φa是E上的單調核算子，則φa是強核算子.

證明設E是對合剩余EQ-代數，φa是E上的單調核算子.因為對任意的x∈E，可得x⊕φa（0）＝x⊕a⊕0＝x⊕a和 φa（x－－）＝a⊕x－－＝a⊕x，所以有x⊕φa0＝φa（x－－）.故由命題3.6知 φa是強核算子.

下面將研究ψa（x）的一些性質及結果.

命題4.2設E是一個剩余EQ-代數，則對任意的a∈B（E）當 且 僅 當 ψa（x）⊙ψa（y）≤ψa（x⊙y）.

證明必要性 假設a∈B（E），因為

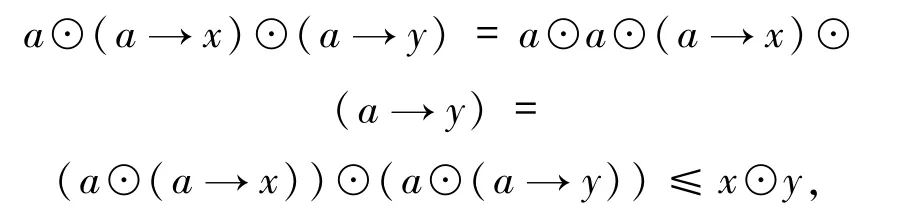
有（a→x）⊙（a→y）≤a→（x⊙y），也就是說，ψa（x）⊙ψa（y）≤ψa（x⊙y）.

充分性 假設 ψa（x）⊙ψa（y）≤ψa（x⊙y），?x，y∈E.令x＝y＝a，則有 ψa（a）⊙ψa（a）≤ψa（a⊙a）.因此，（a→a）⊙（a→a）≤a→（a⊙a）.這就意味著a＝a⊙a，即a∈B（E）.

命題4.3設E是一個剩余EQ-代數，則對于t∈E，t∈B（E）當且僅當?x，y∈E，有x→f t→（y）＝f t→（x）→f t→（y）成立.

證明必要性 設t∈B（E），因為由命題2.3的11）可得?x，y∈E，有

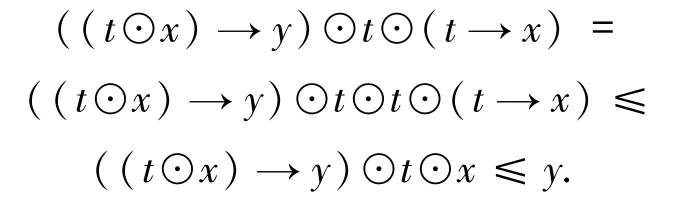
因此，有（t⊙x）→y≤（t⊙（t→x））→y.這樣的話，通過命題2.3的12），有

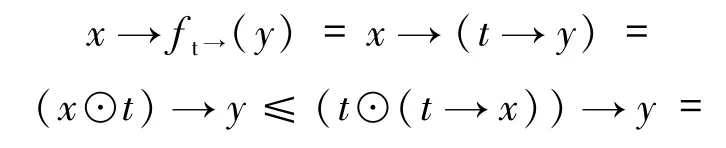
另一方面，由于x≤t→x，容易得出t⊙x≤t⊙（t→x），即（t⊙（t→x））→y≤（t⊙x）→y，由命題2.3的12）可得（t→x）→（t→y）≤x→（t→y），所以有x→f t→（y）＝f t→（x）→f t→（y）.

充分性 如果x→f t→（y）＝f t→（x）→f t→（y），?x，y∈E.令x＝t和y＝t⊙t，可得

t→ （t→ （t⊙t））＝（t→t）→ （t→ （t⊙t））.根據命題2.1.3的12）t→（t→（t⊙t））＝ （t⊙t）→（t⊙t）＝1，可得1＝1→（t→（t⊙t））＝t→（t⊙t）.因此，可以推出t≤t⊙t，而由命題2.3的6）可得t⊙t≤t，故t⊙t＝t，也就是說t∈B（E）.

推論4.4設E是一個剩余EQ-代數并且a∈B（E），則ψa是單調的核算子當且僅當

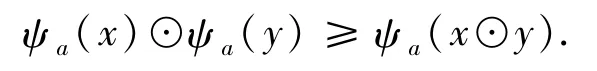
證明必要性 顯然.

充分性 由命題4.3知，對任意的x，y∈E，x→ψa（y）＝ψa（x）→ψa（y）.由假設和定理3.7知 ψa是E上的單調核算子.

命題4.5設E是一個剩余EQ-代數并且a∈B（E），則 ψa（x⊕y）＝ ψa（x⊕ψa（y））.也就是說，如果ψa是單調的核算子并且a∈B（E），則ψa是強核算子.

證明因為y≤a→y＝ψa（y），可得x⊕y≤x⊕ψa（y），由命題2.3的10）有 ψa（x⊕y）＝a→（x⊕y）≤a→（x⊕ψa（y））＝ψa（x⊕ψa（y））.

另一方面，注意到 ψa（u－）＝a→u－＝a→（u→0）＝（a⊙u）→0＝（a⊙u）－和a⊙u－⊙（a→u）≤u⊙u－＝0.也就是說，a⊙u－≤（a→u）－.因為ψa（x⊕ψa（y））＝（a⊙x－⊙（ψa（y））－）－，并且由a∈B（E）可得a⊙x－⊙（ψa（y））－＝a⊙x－⊙（a→y）－≥a⊙x－⊙a⊙y－＝a⊙x－⊙y－.這就意味著對任意的x，y∈E，有

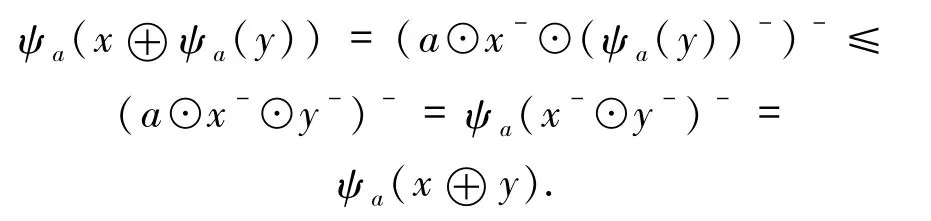
通過以上分析，可以得出，如果a∈B（E），ψa（x⊕y）＝ ψa（x⊕ψa（y））.

下面將考慮另外一個算子 χa（x）＝（x→a）→a，首先研究一下它的基本性質.

命題4.6設E是一個剩余EQ-代數，則對任意的x，y∈E，有（（x→a）→a）→a＝x→a.

證明由x≤（x→a）→a和命題2.3的10）可得（（x→a）→a）→a≤x→a.另一方面，因為（x→a）→（（（x→a）→a）→a）＝ （x→a）→a）→（x→a）→a）＝1.因此，x→a≤（（x→a）→a）→a，（（x→a）→a）→a＝x→a.

引理4.7設E是一個剩余EQ-代數，則對任意的a，x，y∈E，可得x→χay＝ χax→χay.

證明首先證明x→χay≤χax→χay.由于

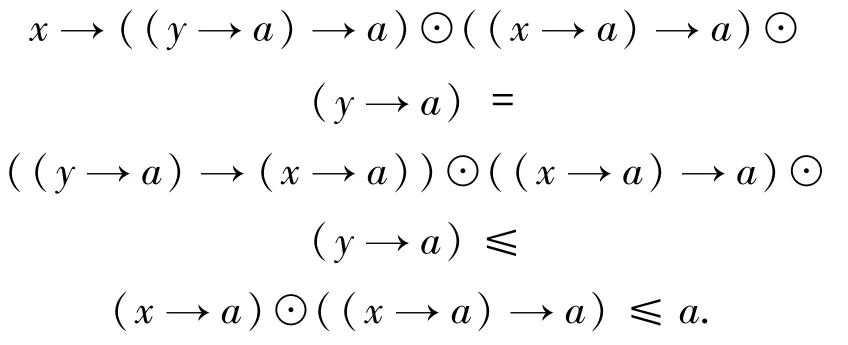
因此

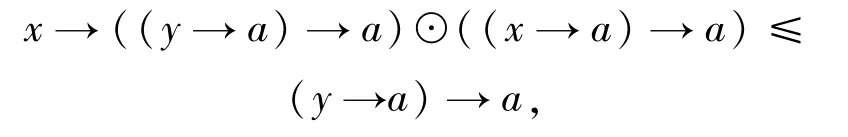
也就是說，x→χay≤χax→χay.

下面證明 χa x→χay≤x→χay.由命題4.6可得

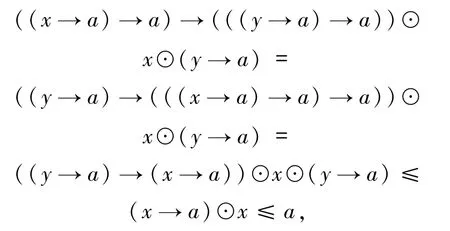
也就是說

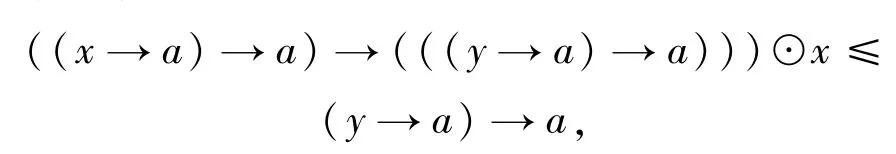
即

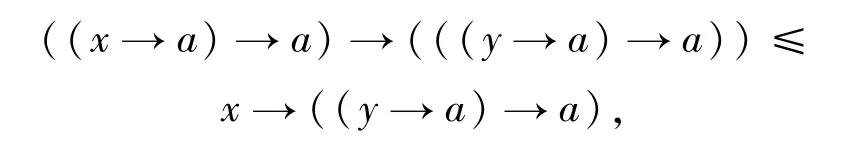
有 χax→χay≤x→χay成立.

通過以上分析可得x→χay＝χax→χay.

推論4.8設E是一個剩余EQ-代數，χa：E→E的一個映射使得 χa（x）＝（x→a）→a，?x∈E，則χa是一個單調的核算子當且僅當 χa（x⊙y）≤χa（x）⊙χa（x）.

定理4.9設E是一個剩余EQ-代數，對任意的x∈E有f t→（x）＝t→x，并且滿足t∈B（E）.如果對任意的x，y∈E有f t→（x⊙y）≤f t→（x）⊙f t→（y），則f t→是E上的單調核算子.

證明1） ?x∈E，則x≤t→x＝f t→（x）.故f t→是增值的.

2）由于t∈B（E），則t→（t→x）＝ （t⊙t）→x＝t→x，即f t→是冪等的.

3）對任意的x，y∈E，可得（t→x）⊙（t→y）⊙t＝ （t→x）⊙t⊙（t→y）⊙t≤x⊙y，也就是說（t→x）⊙（t→y）≤t→（x⊙y），即f t→（x⊙y）≥f t→（x）⊙f t→（y）.另一方面，由假設知f t→（x⊙y）≤f t→（x）⊙f t→（y）.因此

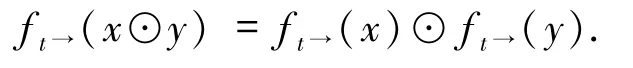
4）由命題2.3的10）知，對任意的x，y∈E，如果x≤y，則t→x≤t→y.也就是說，f t→（x）≤f t→（y），即f t→是單調的.

5 結束語

從邏輯角度來看，核算子作為直覺主義命題邏輯的代數配對物［15］.從代數角度看，核算子及其性質的研究主要用以刻畫代數的結構.本文主要研究EQ-代數上核算子的性質，特別是剩余EQ-代數上核算子性質及核映射下像集的代數結構，并且給出了剩余EQ-代數上強核算子的等價刻畫.隨后，引入3種算子并證明這3個特殊映射與核算子的關系，進一步證明了χa是一個單調的核算子，當且僅當 χa（x⊙y）≤χa（x）⊙χa（y）.

致謝陜西鐵路工程職業技術學院校級項目（KY2019-68）對本文給予了資助，謹致謝意.