矢量控制下的車用永磁電機電磁振動特性分析

洪劍鋒，王善銘，孫旭東，孫宇光，曹海翔

(清華大學 電力系統(tǒng)國家重點實驗室，北京 100084)

0 引 言

電動汽車用永磁同步電動機的電磁振動噪聲水平直接影響著電動汽車的噪聲、振動與聲振粗糙度(noise vibration harshness，NVH)性能。國內外學者針對車用永磁電機的電磁振動問題開展了大量研究，總結如下。

在車用永磁同步電機的振動噪聲機理研究方面，基本都從電機定子三相電流出發(fā)進行磁場、電磁力和電磁振動噪聲的計算。文獻[1-2]采用解析法詳細分析了表貼式永磁電機電磁振動特性和噪聲的預估方法。文獻[3]采用有限元法對6種不同齒槽配合永磁電機的電磁振動進行分析，結果表明兩倍頻電磁振動較大。文獻[4-5]用解析法和有限元法對車用永磁同步電機徑向電磁振動特征，并指出了影響電磁振動的相關因素。文獻[6]提出了一種基于模態(tài)疊加法的車用永磁電機電磁振動估算方法。文獻[7]采用半解析模型計算了考慮電流諧波的永磁同步電機的定子表面振動和噪聲。文獻[8]對電流的影響進行了詳細研究，認為諧波電流會影響電磁力和電磁振動，指出諧波電流的相位是影響的關鍵。文獻[9-10]對永磁電機磁場和電磁力進行了仿真，結果表明，電機中的電磁力隨著負載的增加而增加，但文中并未對引起的原因進行解釋。文獻[11]對異步電機在不同負載工況下的電磁振動進行了實驗測試，結果表明電機在不同的負載工況下呈現不同的規(guī)律，但是并未深入探究。

在汽車用永磁電機的減振降噪方面，主要從設計和控制兩個角度出發(fā)。文獻[12]針對V型轉子永磁電機的電磁振動，提出一種新型隔磁橋的減振優(yōu)化方案。文獻[13]采用轉子分段斜極，文獻[14]采用斜槽方案通過降低電機中的轉矩脈動降低電磁振動。文獻[15]通過在轉子齒上開槽來降低齒槽轉矩和電磁振動。文獻[16]以轉矩脈動和電磁力最小為目標，對轉子鐵心結構進行優(yōu)化來降低電磁振動。文獻[17]提出齒頂偏移結構來降低電機中2倍電流頻率電磁振動。文獻[18]提出一種場重構法，通過優(yōu)化電機電流波形，使得電磁轉矩和徑向力波動最小。文獻[19-20]采用在電機定子中注入補償電流的方案來降低2倍電流頻率電磁振動。雖然這些方案具有一定的可行性，但是并未從矢量控制的角度進行分析和闡述，故不利于對低振動控制方案的指導。

因此，目前針對電機振動的研究，均從定子三相電流出發(fā)而不是dq軸電流出發(fā)推導電磁力特性，這不僅不利于從矢量控制出發(fā)開展電機控制方案設計，也不利于對負載下的電機電磁振動進行分析。基于此，本文從矢量控制的角度出發(fā)對永磁電機的電磁振動機理進行分析，致力于探究負載工況下永磁電機的電磁振動規(guī)律，并對低振動永磁電機電磁振動的矢量控制方案進行指導。

1 矢量控制下的電機電磁力分析

對于電動汽車驅動用永磁同步電機而言，不論是運行在基速下的恒轉矩區(qū)，還是基速上的恒功率區(qū)，常采用矢量控制對其進行驅動。矢量控制的本質是將電機的定子電流解耦為轉矩電流分量iq與勵磁電流分量id，分別實現對電機的轉矩和磁鏈的控制，使得永磁電機獲得良好的動態(tài)性能。當電機工作在非飽和狀態(tài)時，電機中的氣隙磁場Bg可近似為d軸、q軸電流和永磁體產生磁場的疊加，即

Bg(θ,t)=BPM(θ,t)+Bad(θ,t)+Baq(θ,t)。

(1)

式中：BPM為永磁體產生的磁場；Bad為d軸電流id產生的磁場；Baq為q軸電流iq產生的磁場。當忽略齒的影響時，磁場表達式可以寫成：

(2)

(3)

Cpωrt}。

(4)

式中：θ為氣隙中的空間機械角度；p為電機極對數；Bn為永磁體產生的n次諧波磁場幅值；Badv和Badq為繞組電流產生的v次諧波磁場幅值。當v=6k+1時，C為1；當v=6k-1時，C為-1。

圖1給出了永磁體產生的氣隙磁場及其諧波分布。由圖可知，含量主要為基波及奇次諧波分量。圖2為dq軸坐標系下由繞組dq軸電流產生的氣隙基波磁場分布結果。

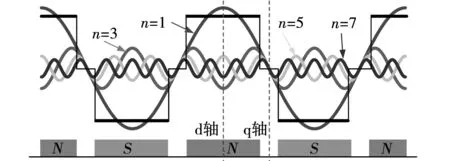
圖1 永磁體產生的磁場Fig.1 Magnetic field excited by PM

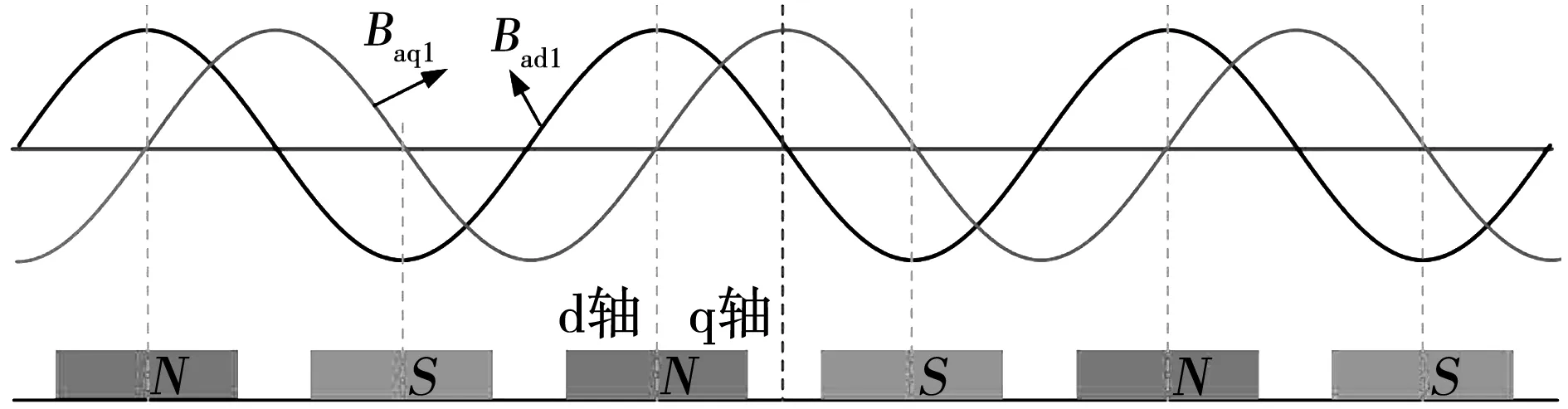
圖2 繞組電樞反應產生的磁場Fig.2 Magnetic field excited by winding current

根據麥克斯韋應力張量法，可得引起電機振動的徑向力波為

(5)

式中：

(n1±n2)pωrt]；

(C1±C2)pωrt]；

(C1±C2)pωrt]；

(n±C)pωrt]；

(n±C)pωrt?π/2]；

(C1±C2)pωrt?π/2]。

當只考慮永磁體和繞組電流產生的基波磁場時，則式(1)可以簡寫成

Bg(θ,t)=Bd(θ,t)+Bq(θ,t)。

(6)

式中：

Bd=(B1-Bad1)cos(pθ-pωrt)；

Bq=Baq1cos(pθ-pωrt-π/2)。

由此，氣隙中的電磁力波式(5)可以寫成

Fmcos(2pθ-2pωrt-φ)。

(7)

式中：

由式(7)可知，電機氣隙中二倍頻電磁力波與永磁體和繞組電流產生的磁場有關。圖3為電磁力波隨繞組產生的dq軸磁場分布變化，永磁體產生的基波磁場幅值為0.8T。由圖可知，當磁場Bad1為0(即id=0)時，電磁力波幅值隨著交軸磁場Baq1的增加而增加。由此可知，隨著電機負載的增加，電磁力波幅值也將增加，這會導致電機的二倍頻電磁振動也增加。在交軸磁場Baq1一定時，電磁力波隨著直軸磁場Bad1的增加而減少。這是由于電機此時工作在去磁工況，d軸磁場減小，從而導致電磁力波的幅值降低，這使得電機的電磁振動將會降低。

②由于系統(tǒng)中各因素的數據量綱不盡相同，不能進行比較，故進行灰色關聯(lián)度分析首先要進行無量綱化的數據處理。

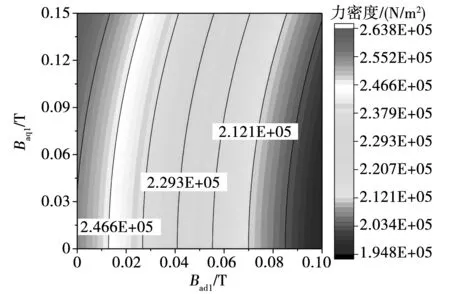
圖3 力密度隨著dq軸磁場變化情況Fig.3 Force density changing with dq-axis magnetic field

由于徑向電磁力是主要的徑向電磁振動源，因此，對電機定子齒部集中電磁力進行分析，作用在第i個齒上的徑向集中力Fr,i(t)可以表示為

(8)

2 仿真分析

利用2D電磁場和3D結構場對一臺6極36槽永磁同步電機的電磁力和定子電磁振動進行仿真，樣機參數見表1，具體仿真流程如圖4所示。

表1 電機模型的參數

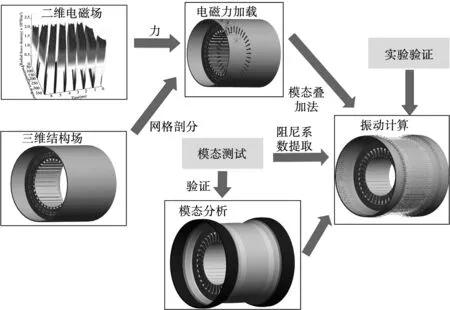
圖4 電機電磁振動有限元分析流程Fig.4 Vibration calculation procedure of the motor

首先采用二維有限元法對電機的磁場和電磁力進行計算，得到各個齒上的徑向力的幅值、頻率和相位信息，其次在三維結構場中對電機的模態(tài)參數進行分析，模態(tài)求取的準確度將對振動計算有重要影響。再次，根據模態(tài)測試實驗，得到電機的阻尼比。最后在三維結構場中，將各齒上的電磁力分別進行加載，采用諧響應分析，即模態(tài)疊加法對電機的電磁振動進行求解。仿真的電機模型考慮了定子鐵心、定子繞組，電機外殼結構，具體的材料特性參數如表2所示。

表2 電機材料特性參數

圖5為某一時刻電機在空載和負載Te=8 N·m工況時，沿靠近定子一層的氣隙單元圓周的徑向氣隙磁場的分布及其諧波分量。由圖可知，氣隙中的諧波分量次數主要為基波及其奇數倍諧波。此外，當電機加載時，由于q軸磁場的引入，電機的空間磁場相位會發(fā)生偏移。而后，采用麥克斯韋應力張量計算了轉子不同位置時電機氣隙中的徑向電磁力，對其在時間和空間上進行分解，圖6給出了二倍電頻率下的電磁力波空間分布結果。

圖5 負載Te=8 N·m時的磁場分析Fig.5 Air-gap flux distribution when Te=8 N·m

由圖6可知，當電機加載時，電機氣隙中二倍頻模數為6的電磁力波幅值從空載的167.5 kN/m2增加到負載時的170.0 kN/m2。此外，其相位也發(fā)生一定的偏移，這說明前面理論分析的正確性。

圖6 負載Te=8 N·m時的二倍電頻率電磁力波Fig.6 Radial force distribution when Te=8 N·m

為了進一步分析電機負載的影響，圖7給出了id=0控制方案下，電機電磁轉矩從0～18 N·m變化時，二倍電頻率模數為6的電磁力波幅值變化曲線。結果表明負載增加時，電磁力波幅值也逐漸增加。

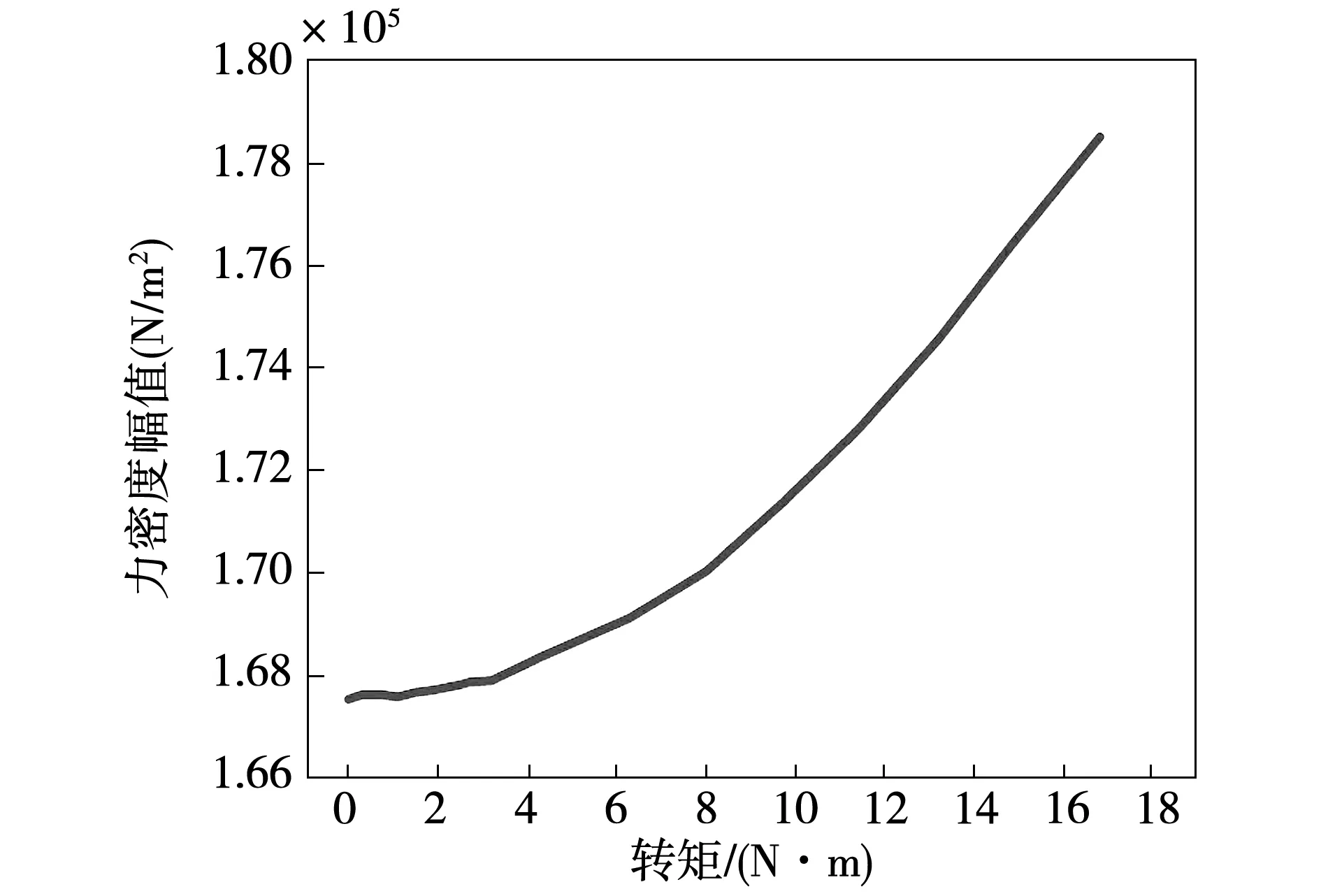
圖7 不同負載下二倍頻電磁力密度幅值Fig.7 Force density at twice fundamental frequency varying with different loads

圖8給出了不同iq電流激勵下定子單齒上的徑向電磁力結果。由圖可得，作用在定子齒部的二倍電頻率集中力，其幅值隨著q軸電流的增加而增加。進一步地，圖9分析了id電流對定子齒部徑向電磁力的影響，圖中id電流為負值，表明其產生的磁場與永磁體產生的磁場相位相反。由圖可看出，在保持q軸電流不變時，增加d軸電流，將使作用在定子齒上的二倍頻電磁集中力逐漸降低，這主要由d軸電流產生的去磁磁場作用的增強導致的結果。

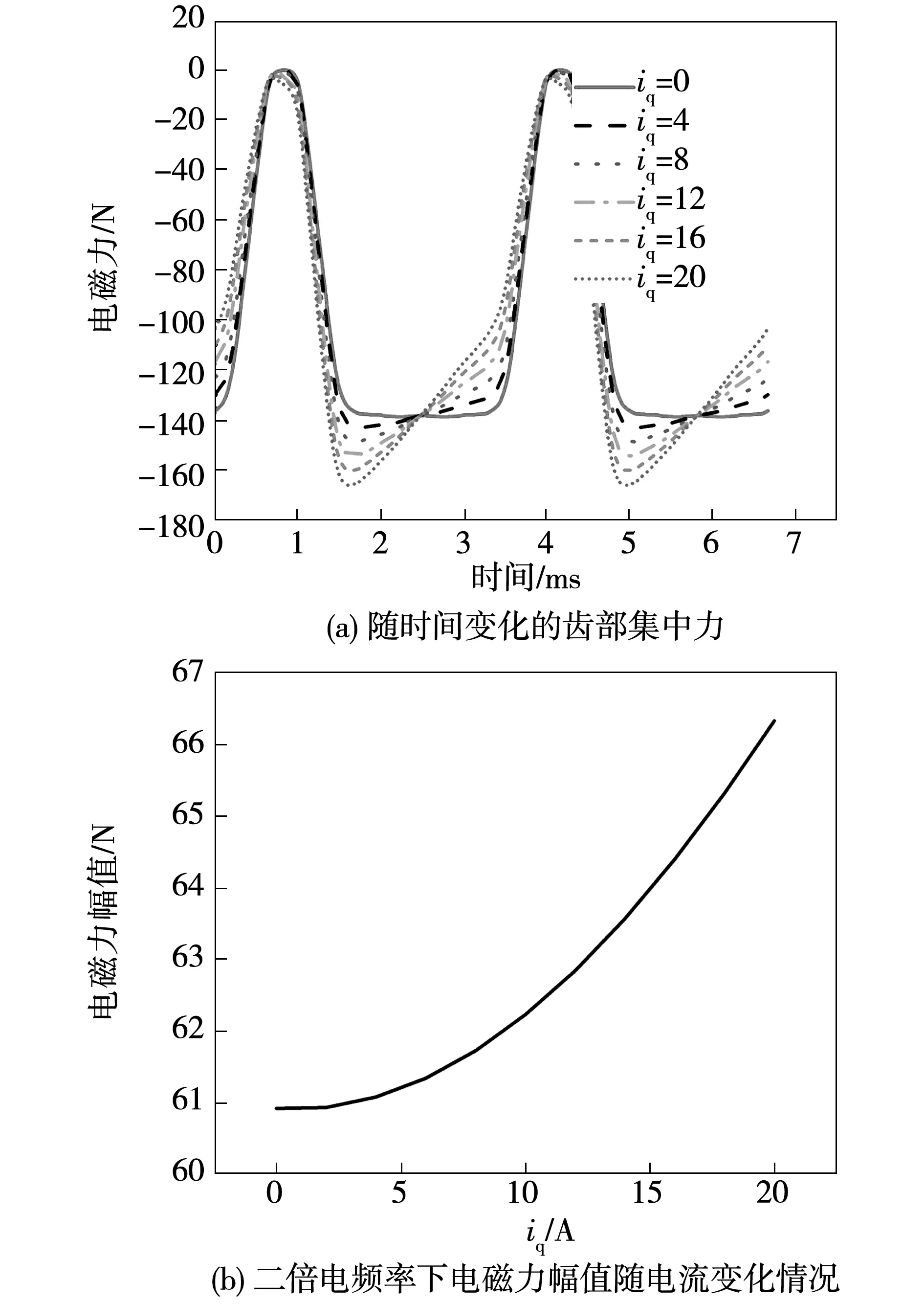
圖8 不同iq電流下的齒部電磁集中力Fig.8 Concentrated tooth force varying with iq

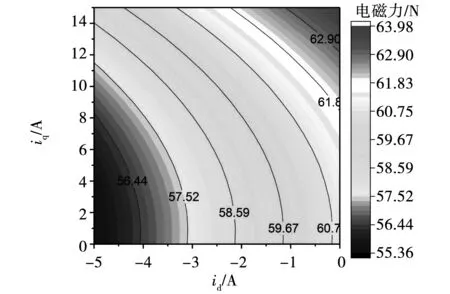
圖9 不同id,iq電流下的齒部電磁集中力Fig.9 Concentrated tooth force varying with id and iq

圖10為不同d、q軸定子電流下永磁電機的電磁轉矩結果，隨著q軸電流iq的增加，電磁轉矩逐漸上升。而隨著d軸電流id的增加，電機中的電磁轉矩降低，但降低幅值不大。

圖10 不同電流下的電機電磁轉矩Fig.10 Electromagnetic torque varying with id and iq

圖11 不同id、iq電流時的電機電磁振動Fig.11 Motor vibration varying with id and iq

由此可知，從電機的轉矩-電流關系圖和電磁振動加速度-電流關系圖中，在保證相同電磁轉矩輸出的前提下選擇合適的d、q軸電流分量以尋求電機的二倍頻電磁振動較小。

3 實驗驗證

為了對理論分析和有限元仿真結果進行驗證，對一臺6極36槽永磁電機進行了實驗測試。實驗中，采用id=0的電機控制方案。圖12為樣機振動測試平臺，電機通過聯(lián)軸器與負載機相連，固定在臺架上。采用型號為PCB 356A32型號的加速度傳感器采集電機機殼表面的電磁振動，采用西門子的SCM205數據處理系統(tǒng)對采集的數據進行處理。采用變頻器對永磁電機進行驅動，測量不同轉速不同負載工況下電機表面的振動加速度值。圖13為電機運行在1 500 r/min、負載為6 N·m時的電機相電流波形。

圖12 實驗裝置Fig.12 Test rig

從圖13可看出，相電流中主要為基波電流，此外，還有3、5、7次諧波電流，但相對于基波電流而言，其幅值均較小，可忽略。圖14給出了此種工況下電機的電磁振動波形。

圖13 電機在1 500 r/min轉矩6 N·m時的電流波形Fig.13 Measured stator currents of the motor at 1 500 r/min under Te=6 N·m

由圖14可知，電機在兩倍電頻率(150 Hz)處的振動加速度為0.12 m/s2，大于其他頻率下的振動加速度。為了對負載的影響進行驗證，完成了3種轉速(900、1 200和1 500 r/min)6種負載(轉矩1～6 N·m)工況下的電機振動測試，二倍電頻率下的振動加速度幅值結果如圖15所示。由圖可得，在同一個轉速下，隨著電機負載的增加，電機電磁振動幅值也增加，這驗證了理論分析和仿真結果。此外，對于同一個負載而言，當轉速越高，電機的電磁振動越大。

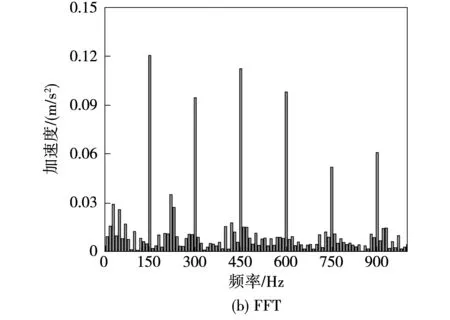
圖14 電機在1 500 r/min轉矩6 N·m時的電磁振動加速度Fig.14 Measured vibration acceleration of the motor at 1 500 r/min under Te=6 N·m

圖15 電機在不同轉速轉矩下的電機二倍頻電磁振動Fig.15 Measured vibration acceleration at twice fundam-ental frequency of the motor at different speed and toque

4 結 論

本文從矢量控制的角度分析了永磁同步電機的電磁振動規(guī)律，基于磁場定向的理論分析了電機在負載工況下的電磁力和電磁振動特點。采用多物理場有限元仿真研究和實驗分析電機不同轉速下的電機振動規(guī)律，對理論分析結果進行了驗證，得到以下結論：

1)隨著電機負載增加(q軸電流的加大)，氣隙磁場中的基波含量增加，導致二倍頻下的電磁力增加，從而加劇了電機的電磁振動。

2)不同d、q軸電流將導致不同的電機電磁振動和電磁轉矩，可以通過選擇合適的d、q軸電流以使電機的電磁振動降低。

本文的研究成果有利于在矢量控制方案中直接控制d、q軸電流分量來達到控制電磁力和電磁振動的目的，可以在電機設計和控制階段評估電機的電磁振動性能。