基于多尺度排列熵和線性局部切空間排列的機械故障診斷特征提取

趙建崗， 寧 靜,2， 寧云志， 陳春俊， 李艷萍

(1. 西南交通大學 機械工程學院， 成都 610031； 2. 軌道交通運維技術與裝備四川省重點實驗室， 成都 610031)

過去的三十年中，基于信號處理方法的特征提取算法在機械領域被廣泛研究[1]，在文獻[2]中，用近似熵(approximate entropy,ApEn)監測滾動軸承的健康狀況。然而ApEn嚴重依賴于數據長度，并且其估計值總是低于處理短數據集時的預期值。為了克服這種不足，提出了樣本熵(sample entropy,SampEn)[3]，由于SampEn值對數據長度不敏感并且不受信號中的噪聲影響，因此它受到了很多關注。然而ApEn和SampEn僅在單一尺度上估計復雜性，當他們應用于多時間尺度時效果極差。為克服這個弱點，在文獻[4]中提出了多尺度熵(multiscale entropy, MSE)。但MSE對故障診斷復雜性的估計不準確。另外用它處理長時間序列時特別耗時[5]。

近年來，引入排列熵(permutation entropy,PE)[6]來計算機械系統的復雜性[7-8]。但是與AnEn和SampEn一樣，PE只能通過單一尺度分析時間序列，即可能會丟失嵌入其他尺度的許多有用的故障信息。但是某些地區機車和機床的操作環境也非常苛刻和復雜[9-10]，監控系統收集的大量信號通常是非靜態和非線性信號。由于機械組件之間的相互作用和耦合效應，這些獲得的信號包含多種自然振動模式，這導致單尺度特征提取方法不能理想地表達這些信號[11]。為克服這一缺點，提出了多尺度排列熵(multiscale permutation entropy,MPE)[12]來估算不同尺度上時間序列的復雜性。在文獻[13]中MPE用于提取滾動軸承的故障特征，并且驗證了MPE的性能優于PE。

通常在使用MPE進行特征提取之后，特征矩陣的維度將非常高。提高故障識別的準確性，需要降低高維特征矩陣的維數以獲得低維主要特征，即降維[14]。主成分分析(principal component analysis,PCA)[15]是經典的降維算法，但其僅對線性和高斯數據有效，并且在處理非線性或非平穩信號時經常不能達到理想的效果。最近流形學習被用來提取嵌入在非線性高維數據中的低維內在結構，而且它已被用于機械故障診斷[16-17]。其中以線性局部切線空間排列(linear local tangent space alignment,LLTSA)[18]性能較好，本文采用LLTSA進一步提取嵌入在由MPE計算的高維特征矩陣中的低維主要特征。

丁吉等[19]用同步壓縮小波變換對發電機的連桿軸承進行時頻分析，為發電機相關性能和工況的保障提供了重要的估計方法。孫自強等[20]用小波分形方法計算了風機組軸承時域波形的關鍵維數，可以確定軸承的故障形式。向丹[21]等利用LLTSA對特征進行降維，并通過SVM對故障類別進行辨識。蘇祖強等[22]通過LLTSA與加權k最近鄰分類器提高了故障分類的精度。熊慶等[23]研究了多重分形趨勢波動分析特征參數的敏感性和穩定性，并成功運用于滾動軸承的定量故障診斷。李永健等[24]通過改進的多尺度排列熵對列車的軸箱軸承進行了診斷研究，取得了較好的效果。

本文將MPE算法在多尺度信息處理上的優越性和LLTSA在非線性數據強適應性相結合應用于軸承的故障診斷，用兩個軸承箱數據對MPE-LLTSA方法進行了測試，測試結果表明了該方法在機械模式分類和故障識別領域的應用潛力。

1 理論背景

1.1 MPE的簡介

1.1.1 MPE算法

多尺度排列熵(MPE)被定義為不同尺度時間序列的一組PE值。MPE算法包括兩個步驟：① 應用粗粒度過程從原始時間序列獲得多尺度時間序列;② 計算每個粗粒度時間序列的PE值。這兩個步驟可以簡要總結如下[25]。

(1)

(2) 在MPE分析中，每個粗粒度時間序列的PE值由式(1)～(5)計算并且比例因子s的函數可以表示為

(2)

1.1.2 MPE的參數選擇

在MPE算法中，需要設置四個參數，嵌入維度m，時間延遲τ，時間序列長度N和比例因子s。其中嵌入維度m決定輸入的狀態數量m!，并且PE值高度依賴于m的選擇。如果m太小該方法將無法工作，因為不同狀態太少。但是如果m太大，由于條件N≥5m!，可能會對隨后的多尺寸研究造成相當大的不便[26]。Bandt等指出尺寸m應滿足3≤m≤7。為了檢測信號的動態變化，通常通過信息損失和計算復雜性之間的權衡關系來選擇嵌入維數m。因此本文中m設為4。時間延遲τ對結果幾乎沒有影響，所以我們在本文中將τ設置為1。時間序列N的長度對PE值的估計有很大影響，N越大計算時間越久。而太小的N不能滿足條件N≥5m!。考慮到這些約束，我們在第3章的模擬試驗中將數據長度N設置為400，將比例因子s設置為7。在第4章的研究中，N設置為1 200，s設置為12。

1.2 線性局部切線空間排列

線性局部切線空間排列(LLTSA)[27]是一種經典的流形學習算法，它可以提取高維數據集的固有幾何信息，即挖掘隱藏在高維觀察空間中嵌入的低維流形，從而不會丟失數據中的重要信息[28-29]。

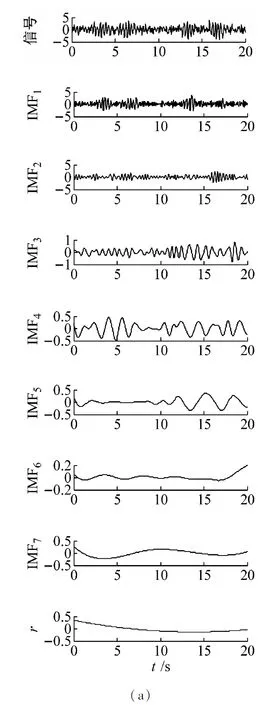
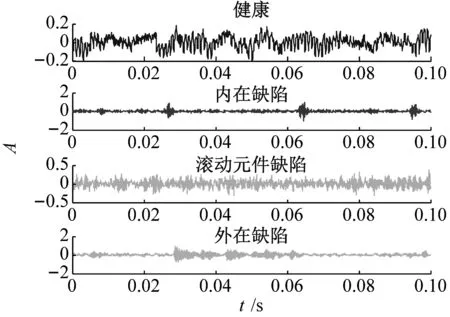
假設一個高維數據集X={x∈(R)D,i=1,2,…,N}，它是從屬于(R)d的較低維特征空間的基礎流形中采樣的，其中D和d(d

Y=ATXHN

(3)

式中:HN=I-eeT/N表示中心矩陣;I表示單位矩陣;e表示所有元素等于1的列向量。 LLTSA的基本假設是每個樣本附近的局部結構信息可以用其局部切線空間表示。因此為構建從高維輸入空間到低維特征空間的投影矩陣，可以在全局低維特征空間中重新排列所有樣本的局部切線空間。

在LLTSA算法中，根據樣本之間的歐幾里德距離構造采樣點xi(i=1,2,…,N)的鄰域xi=[xi1,xi2,…,xik]，其中k表示最近樣本的數量。然后用局部變換矩陣Qi來將鄰域xi映射到局部低維切線空間。因此樣本點xi附近的局部結構可以近似表示為

(4)

獲得局部結構后，為得到X的全局低維表示Y，將所有樣本的局部切向空間重新排列在全局低維特征空間中，選擇矩陣為S=[S1,S2,…,SN]其中Si(i=1,2,…,N)是0-1的選擇向量，因此Yi=YSi，其中Yi=[yi1,yi2,…,yik]是Xj的全局低維表示。此步驟的目標函數可以轉換為以下最小問題

(5)

(6)

式中,B=SWWTST。用ATXHNBHNXTA=Id確定唯一的Y。最后式(4)的解轉化為廣義特征值問題為

ATXHNBHNXTα=λXHNXTα

(7)

可以由對應于式(7)的特征向量λ1≤λ2≤…≤λd的d個特征向量α1,α2,…,αd得到轉換矩陣A，即A=α1,α2,…,αd。

2 基于MPE-LLTSA的特征提取方法

故障診斷中，對于經常出現在機械領域中的非線性信號，特征選擇是一個難題。EEMD因為其自適應性而被廣泛用于處理這種非平穩信號。流形學習在非線性信號中具有更強的降維能力[30]，因此本文引入了流形學習算法LLTSA。本文將該特征提取方法縮寫為EEMD-LLTSA, EEMD-LLTSA的技術路線及其識別方法如圖1(a)所示。

(a) EEMD-LLTSA

然而在復雜的機械設備中，監測系統收集的大量非線性信號通常包含多種自然振動模式，這導致單尺度特征提取通常無法表征這些信號。因此引入多尺度方法MPE來改善傳統基于單尺度的非線性動態參數的性能。首先通過使用MPE計算信號x(t)以獲得一組熵值{HMN1,HMN2,…,HMNs},其中s是比例因子。然后構建具有高維度的樣本矩陣V，用LLSTA挖掘高維樣本特征矩陣V中的固有結構以適應低維特征矩陣。最后用LSSVM建立診斷模型進行狀態分類。本文將該特征提取方法縮寫為MPE-LLTSA，MPE-LLTSA特征提取方法及其條件識別的技術路線如圖1(b)所示。詳細步驟描述如下：

步驟1參數選擇：時間序列x(i),k=1,2,…,N，相應參數有嵌入維數m，時間延遲τ，時間序列N的長度和比例因子s。

步驟2MPE算法計算信號的多尺度熵值為

(8)

步驟3對所有樣本進行步驟1和2，構建高維樣本特征矩陣V為

(9)

式中,p代表樣本數量。

步驟4通過流形學習降低維數：使用LLTSA降低樣本特征矩陣V的維數以獲得低維特征向量，如下面的公式所示

(10)

式中:fn表示第n維特征;d是嵌入維度。

步驟5訓練和識別：將獲得的低維流形特征分為訓練樣本和測試樣本，并使用LSSVM實現狀態識別。

3 試驗探究

3.1 模擬試驗

3.1.1 信號模擬

非線性信號通常具有調幅[31]的特性，這經常出現在機械領域。根據振動信號構造兩個調幅信號來驗證MPE-LLTSA特征提取方法的性能。

w(t)=am·[1+mcos(2πfmt)]·sin(2πfct)

(11)

式中，am=1，m=8,fm=0.3 Hz，fm=0.3 Hz。對于第一信號w1(t)，fc,1=3，對于第二信號w2(t)，fc,2=3.1 Hz，采樣頻率為20 Hz。

下面用隨機生成的混合矩陣模擬三個復雜信號。

(12)

通過上述矩陣M對w1(t)和w2(t)執行矩陣運算

(13)

添加三個隨機高斯噪聲n1(t),n2(t) 和n3(t)以分別生成新信號a(t),b(t)和c(t)，如圖2所示。

(a)

(14)

3.1.2 特征評估

如圖2所示，箭頭處的那三個模擬信號的幅度是不同的，但差異不是那么明顯。根據它們的波形無法準確區分這三個信號。為了通過頻率特征區分三個信號，將FFT方法引入上述三個模擬信號，分別生成其頻域圖，如圖3所示。可以看出，通過FFT獲得的這三個頻域圖之間的差異并不明顯。通過FFT，我們同樣無法準確地區分這些有調制特性的非平穩信號。最后引入Hilbert-Huang變換(HHT)來分析這三類信號的時頻特性，譜圖的結果如圖4所示。它表明這些簡單的時頻分析方法無法準確識別出三個信號。

(a)

(a)

上述時頻分析方法無法準確識別這三種信號。為了解決這個問題，引入了MPE-LLTSA特征提取方法。為每種類型的信號選擇60個樣本，總共180個。每個樣本的數據長度N設置為400，時間長度為20秒。如1.1節所示，在MPE算法中，分別設置三個參數，嵌入維數m，時間延遲τ和比例因子s。在本次研究中，我們設定m=

4,τ=1和s=7。如1.2節所示，在算法LLTSA中，根據文獻[32]，兩個參數鄰居數k和內在維度d分別設置為7和3。a(t),b(t)和c(t) 的每個樣本的MPE結果顯示在圖5中。通過MPE計算所有樣本以重建180×12高維特征矩陣。然后通過使用LLTSA方法獲得180×3的低維特征矩陣。降維后的結果如圖6(a)所示。可以看出這三個模擬信號可以通過MPE-LLTSA算法完全分離，得到的不同信號的三維特征高度集中，聚類效果極佳。為了證明LLTSA方法的優越性，還引入了PCA方法。聚類效果如圖6(b)所示。結果表明，MPE-PCA特征提取方法 還可以準確識別三個模擬信號，聚類效果也非常好。它表明MPE特性可以有效地克服信號中的噪聲影響，適用于非線性信號處理。

圖5 三個模擬信號的MPE特征

(a) MPE-LLTSA

為了證明MPE-LLTSA優于EEMD-LLTSA方法，引入了機械中常用的能量和SampEn功能進行仿真分析。根據文獻[32]在EEMD算法中集合數和信噪比(SNR)兩個參數分別設置為100和0.3。首先所有樣本都通過EEMD進行分解，α(t),b(t)和c(t)的每個樣本的結果如圖7所示。由于EEMD是主成分分析方法，因此信號的主要信息包含在前幾個IMF中。此外所有樣本獲得的IMF數量須大于6。因此為了確保EEMD-LLTSA方法的后續處理，提取前六個IMF的能量和SampEn特征以分別構造180×6高維特征矩陣。然后通過LLTSA算法減少特征矩陣以生成180×3的低維特征矩陣(參見圖8)。從圖7和圖8可知，EEMD-energy-LLTSA特征提取方法可以分離三類信號，但聚類效果明顯差于MPE-LLTSA和MPE-PCA。EEMD- SampEn-LLTSA方法甚至無法分離這三個模擬信號，因為在特征提取過程中，單尺度特征提取方法僅考慮信號的一個單尺度信息。在某種程度上，它忽略了其他維度中包含的故障信息。這種單尺度特征提取方法經常無法在具有嚴重故障信息耦合的機械設備實現期望的結果。

圖7 模擬信號α(t),b(t)和c(t)的EEMD結果

(a) EEMD-energy-LLTSA

3.1.3 聚類評價

為了準確地評估聚類能力，引入了三個評價指標，即類內散射Sw，類間散射Sb和比率Sw/Sb以描述聚類效應。對于特征向量[f1，f2,…,fd]，d是嵌入維度，參數Sw和Sb的定義為

(15)

(16)

通過計算類內離散度Sw，類間離散度Sb和比率Sw/Sb，可以獲得3.1.2節中實現的特征的準確評估，如表1所示。結果表明，MPE-LLTSA方法具有良好的分類和聚類能力，優于MPE-PCA和EEMD-LLTSA方法。

表1 對三種信號的不同特征進行聚類評估

3.2 機械故障診斷試驗結果

從滾動軸承系統測量的信號非常復雜。為了進一步驗證MPE-LLTSA方法的有效性，在這一節中將使用Case Western Reserve University提供的滾動軸承的試驗數據[33]。軸承試驗系統及其示意圖如圖9所示。它由2馬力的馬達(左)，扭矩傳感器(中心)，測功機(右)和控制電子設備(未示出)組成。試驗軸承是6205-2RS JEM SKF深溝球軸承，局部單點損壞分別使用電火花加工機設置在外滾道，內滾道和滾動體的位置。本文中的振動信號取自安裝在驅動端的加速度計，采樣頻率為12 kHz。

圖9 滾動軸承試驗系統草圖

3.2.1 四類情況

這種情況下，分析包括健康，內在缺陷(IRD)，滾動元件缺陷(RED)和外在缺陷(ORD)在內的四類情況。本節中的振動信號從損壞0.178 cm的軸承中收集。數據長度N設置為1 200。訓練和測試樣本的數量在表2中給出。引入MPE-LLTSA來識別這四個信號。如1.1.3節所述，在MPE方法中我們設置m=4，τ=1和s=12。四個信號的波形如圖10(a)及其MPE結果如圖10(b)所示。對所有樣品通過MPE構建高維樣本特征矩陣之后用LLTSA降維得到低維特征。在LLTSA方法中，我們設置k=7和d=3。計算結果如圖11(a)所示，表明MPE-LLTSA可以完全分離這四個信號。為了驗證我們提出的MPE-LLTSA方法的優越性，還計計算了MPE-PCA和EEMD-LLTSA結果，如圖11(b)，圖11(c)和圖11(d)所示。為得到精確的評估，還計算了類內離散度Sw，類間離散度Sb和Sw/Sb，如表3中所示。最后引入LSSVM方法識別四種狀態，正確的識別率如表3所示。從圖11和表3可知MPE-LLTSA方法可以區分這四種狀態，且其聚類效果優于MPE-PCA和EEMD-LLTSA。

表2 不同檢測的試驗數據的詳細描述

(a)

(a) MPE-LLTSA

表3 不同檢測下不同特征的聚類評價

3.2.2 五種狀態

在表4所示的情況下，分析了滾動體的五種不同的滾動軸承故障(健康的，0.178 cm，0.356 cm，0.533 cm和1.02 cm)，詳細信息顯示在表4中。數據長度N選擇為1 200，訓練和測試樣本的數量分別為50和50。在MPE方法中，我們設置m=4，τ=1和s=12。在LLTSA方法中，我們設置k=7和d=3。五個信號的波形圖如圖12(a)及其MPE結果如圖12(b)所示。MPE-LLTSA的計算結果如圖13(a)所示。為了做比較，在圖13(b)，圖13(c)和圖13(d)中列出了MPE-PCA和EEMD-LLTSA的結果。為了評估更精確，還在表5中計算了三個參數Sw，Sb和Sw/Sb。最后引入LSSVM方法識別五種狀態，并在表5中列出正確的識別率。從圖13和表5，我們可以看到MPE-LLTSA可以完全分離出五類故障，分類結果和聚類效果優于MPE-PCA和EEMD-LLTSA。測試結果表明，MPE-LLTSA方法可用于軸承缺陷嚴重性評估。

表4 五個檢測嚴重程度的試驗數據的詳細描述

(a)

(a) MPE-LLTSA

3.3 討 論

我們提出的MPE-LLTSA方法的優點主要是由于以下兩個原因：

(1) 能量和SampEn等單尺度特征提取方法只能分析單個尺度的時間序列，導致隱藏在其他尺度中的有用信息丟失。然而非線性或非平穩信號通常包含多種自然振蕩模式，并且故障信息通常是復雜的并且總是隱藏在多尺度時間序列中。MPE方法可以估算不同尺度的時間序列的復雜度，可以有效地克服信號中的噪聲影響。

(2) 在模式識別領域，由EEMD，MPE等計算出的特征矩陣的維數通常很高，難以直接識別這些高維特征。為了提高識別精度，有必要進一步提取嵌入在高維特征空間中的低維主要特征。LLTSA具有良好的減小高維非線性數據維度的能力。

4 結 論

本文提出了一種用于機械故障診斷的MPE-LLTSA特征提取方法。由于機械設備結構復雜，操作環境惡劣，監測系統采集的大量非線性信號通常包含多種自然振動信號，單尺度特征提取方法往往無法表征這些信號。為了解決這個問題，引入MPE來提取非線性信號的多尺度特征并構建高維特征矩陣。隨后用LLTSA挖掘嵌入的內在結構并進行低維特征提取。最后用LSSVM進行機械故障診斷。同時還引入了一些特征提取方法，包括MPE-PCA和EEMD-LLTSA進行比較。仿真和實際案例的測試結果表明，我們提出的MPE-LLTSA方法具有良好的分類和聚類能力，與其他方法的比較結果證明了我們提出的MPE-LLTSA方法在機械故障診斷領域的價值和應用潛力。