一種基于時空瞬時穩定性的方位譜估計方法

王林生, 王慧婷, 劉志剛

(1.河南省工業嵌入式網絡控制工程技術研究中心，河南 南陽 473009；2.河南工業職業技術學院，河南 南陽 473009；3.北京郵電大學 科學技術發展研究院，北京 100876；4.南昌大學安全仿真模擬實驗室，南昌 330031)

空間方位譜估計一直是雷達、聲納等領域中重要的研究課題，為了降低空間方位譜估計方法對原始數據最低信噪比需求，人們常采用布陣與信號合成方式提高輸出信噪比，等價于降低了空間方位估計方法對原始數據最低信噪比需求[1-2]。為了能夠對360°水平范圍內空間目標實現等分辨率方位估計，研究學者提出通過布放圓陣方式實現[3-6]；另外，為了提高圓陣空間方位譜估計分辨率，在信號處理方面，研究學者提出采用子空間分解方式實現高分辨方位估計(本文稱之為子空間分解方法)，并對該方法進行了工程化應用[7-8]。

由于現有子空間分解方法在對一幀數據進行協方差估計中，首先將一幀時域多個采樣數據通過傅里葉變換轉換為不同頻點頻域數據，實現頻域壓縮采樣；然后再對每一頻點利用頻域單個數據求取該頻點協方差矩陣；最后通過多幀頻域數據累積實現協方差矩陣估計[9-10]。由于受時頻轉換中頻率分辨率限制，單幀時頻轉換需要一定長度時域數據，致使在空間數據非平穩時，難以通過頻域多幀數據累積實現協方差矩陣估計，影響子空間分解效果，對實際應用帶來了一定的限制[11-12]。為了提高子空間分解方法在實際應用中的穩健性，研究學者從混沌優化思想[13]、自適應迭代加權思想[14]、壓縮感知思想[15-16]、滑動平均思想[17]提高了子空間分解方法的目標檢測性能，但以上思想均是對如何實現協方差矩陣估計，并未考慮在協方差矩陣估計之前進行陣增益轉換預處理。

針對基于子空間分解的空間方位譜估計方法穩健性問題，本文提出一種基于時空瞬時穩定的方位譜估計方法。該方法可將短時內獲得的足夠多的采樣數據轉換為協方差估計所用快拍數，通過多個快拍數據累積實現滿秩協方差矩陣穩定獲取，降低空間數據穩定性對子空間分解產生的影響；同時在無目標先驗信息情況下，依據各子空間方位譜峰值索引離散度差異，通過對各子空間方位譜進行判決處理，降低背景噪聲對最終合成方位譜影響。數值仿真及實測數據處理結果進一步驗證了所述方法的有效性和可行性。

1 子空間分解方法

1.1 基本原理

(1)

式中:W(θ)=[ej2πfτ1,ej2πfτ2,…,ej2πfτN)]為導向權向量;N為傳感器數。

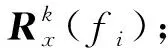
(2)

1.2 空間數據影響分析

在頻點fi上，第k幀數據的協方差矩陣可表示為

(3)

同時，由文獻[18]可知，一次處理數據幀數K對子空間分解方法的影響可近似表示為

(4)

式中，σP(θ)為子空間分解方法所得空間目標方位估計方差。

由式(4)可知，在傳感器數N一定時，一次處理數據幀數K對子空間分解方法影響較大。

2 本文方法

2.1 基本原理

由傅里葉變換分析可知，對于一幀多個時域數據經過傅里葉變換后，在頻域同一頻點只包含單個頻域數據，再利用單個頻域數據求取不同頻點協方差矩陣時，容易出現非滿秩現象，且會導致信干噪比損失較大。對此，本文依據空間目標信號時域瞬時穩定性，通過復解析變換，將多個時域數據轉換為多個復域數據，通過多個復域數據的累積，提升協方差矩陣穩定性。

(5)

式中，w為角頻率。

(6)

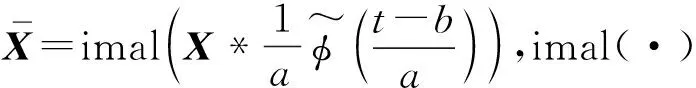
通過選擇小波函數參數(如帶寬參數、中心頻率和尺度伸縮因子)，可在對接收陣拾取數據實現復解析變換處理中抑制分析頻帶以外背景噪聲，具體證明可參考文獻[19]。

其次，根據相位與時延之間的關系，在搜索角度θ上，對各傳感器復域數據Y按τn=(rcos(θ-(n-1)α))/c進行時延補償，c為聲速，r為接收陣半徑，α=2π/N，1≤n≤N，N為接收陣所含傳感器數量，得經時延補償后數據。

(7)

式中，φτn=[φτ1,φτ2,…,φτN]T，φ0=[φτ01,φτ02,…,φτ0N]T，τ0n=(rcos(θ0-(n-1)α))/c，θ0為空間目標相對接收陣方位。

(8)

最后，對延時補償后的各子空間對應特征向量互相關矩陣求和，求取該幀數據各子空間對應空間方位譜；并利用各子空間對應空間方位譜峰值索引離散度差異[20]，對各子空間方位譜按式(9)進行加權處理，得到最終合成方位譜。

(9)

式中:由于不知道目標信源個數，方位求和加權處理中對所有子空間合成方位譜進行加權處理，I1×N=[1,1,…,1]1×N為1×N單位矩陣;αn為合成方位譜過程中第n個子空間對應的加權因子。

2.2 方法實現

本文方法可分為以下幾個步驟實現。

輸入：對接收陣拾取數據x(t)。

步驟1對接收陣拾取空間數據按式(6)進行復解析小波變換和分幀處理(相鄰兩幀之間按L=0.5I長度進行重疊處理)，得到K幀復域數據Y，并令處理數據幀號k=1；

步驟2按式(7)所示，在搜索角度θ上，對第k幀復域數據Y進行時延補償；

步驟4采用常規波束形成思想，按式(10)所示，得到第k幀數據對應的各子空間方位譜Pn(k,θ)，1≤n≤N；

(10)

步驟5更新搜索角度θ，重新執行步驟2～步驟4，直到θ=Θ結束，得到各子空間方位譜Pn(k,θ)在0°≤θ≤Θ上各個值；

步驟6搜索各子空間方位譜Pn(k,θ)，0°≤θ≤Θ，1≤n≤N最大值索引，得到該子空間方位估計值；

(11)

步驟7更新處理幀數據，k=k+1，重復執行步驟2～步驟6，直到k=K，則各子空間均得到K個方位譜Pn(k,θ)和方位估計值θmax(k,n)，k=1,2,…,K。

步驟8求取各子空間方位譜峰值索引的離散度，記為σθmax(n),n=1,2,…,N。

(n=1,2,…,N)

(12)

(k=1,2,…,K;n=1,2,…,N)

(13)

式中，Cm和M分別為最小二乘擬合系數和階數。

步驟9在無目標先驗信息情況下，根據各子空間方位譜峰值索引離散度求取各子空間方位譜加權因子。

n=1,2,…,N

(14)

步驟10利用各子空間方位譜加權因子對各子空間方位譜進行加權處理，得到下最終合成方位譜

(15)

2.3 估計能力分析

令接收陣所在空間只存在1個空間目標，空間目標相對接收陣方位為θ0，對應子空間編號為N。由空間目標子空間方位譜所得方位估計值(最大值索引)范圍為[θ0-Δθ0,θ0+Δθ0]，其中Δθ0為空間目標子空間方位譜對應方位估計誤差；由非目標子空間方位譜所得方位估計值(最大值索引)范圍為[θmin,θmax]，其中θmin和θmax分別為方位掃描角度最小值和最大值。令，空間目標和非目標對應子空間方位譜的方位估計值方差分別為σs和σn。

(16)

為了進一步說明本文方法通過對各子空間方位譜進行最大值索引離散度判決處理，可有效提高空間目標對應子空間方位譜在最終合成方位譜中的比重，降低了背景噪聲對子空間分解方法的影響。

首先，對N-1個非目標子空間方位譜進行統計。對于非目標子空間方位譜，每個方位對應索引在每幀方位估計中出現概率相等。

(17)

然后，將空間目標方位譜方位估計值對應方差加入上式，可得到：

(18)

上式可進一步簡化為

(19)

圖1為不同方位估計范圍所得方位估計方差理論值和仿真值。

圖1 不同方位估計范圍下方位估計方差

當空間目標對應子空間方位譜每幀方位估計值均接近于空間目標方位真值時(Δθ0≈0°)，非空間目標子空間方位譜方位估計范圍在0°≤θ≤Θ，由圖1可得，σs<<σn，即

(20)

3 驗證分析

3.1 數值仿真分析

為了進一步驗證本文方法在方位估計方面的性能，接下來進行如下幾方面數值仿真。

表1 數值仿真參數

3.1.1 多目標方位估計分析

數值仿真中，噪聲為空間高斯白噪聲經過128階濾波器濾波所得帶限噪聲，頻帶寬度與目標信號帶寬一致，信噪比計算方式為

(21)

式中:lg(·)為以10為底對數;var(·)為方差函數;sig(t)為目標信號;noise(t)為帶限噪聲;t為采樣時刻。

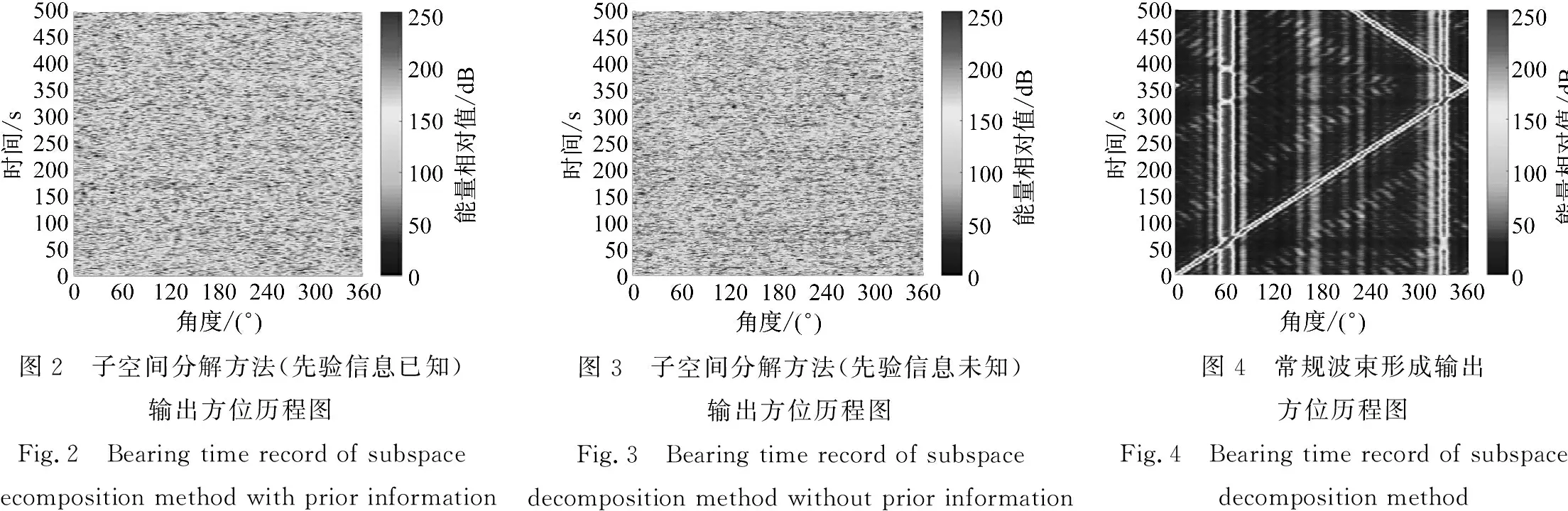
圖2～圖7仿真結果表明：在該仿真條件下，在無目標先驗信息情況下，子空間分解方法已無法對空間目標實現方位估計，而本文方法可以對4個空間目標實現方位估計；在有目標先驗信息情況下，子空間分解方法對空間目標實現方位估計效果遠差于常規波束形成和本文方法；對于60°和68°處空間目標，常規波束形成已無法對其實現有效分離，而本文方法卻可以很好地將其分開，進一步驗證了本文方法保持了子空間分解方法在分辨率上的優勢，相比常規波束形成具有較好的方位分辨率。另外，在背景噪聲級方面處理上，本文方法好于常規波束形成，而子空間分解法最差。

以上現象原因在于子空間分解方法需要多幀數據的頻域累積才能滿足協方差矩陣的滿秩條件，當空間數據存在不穩定時，會導致失配現象產生；而本文方法通過復域處理，采用一幀時域數據即可滿足協方差矩陣的滿秩條件，同時采用圖 8所示加權因子αn對各子空間方位譜進行加權處理，在無目標先驗信息情況下，有效提升了編號21～24子空間(空間目標信號子空間)方位譜在最終合成方位譜中的比重，降低了背景噪聲對合成方位譜的影響。

3.1.2 方位估計性能統計分析

為了進一步驗證本文方法對空間目標方位估計性能的統計特性，對上述仿真中60°處目標進行檢測和方位估計統計分析，在SNR=-30 dB～0情況下，圖9和圖10分別給出了由子空間分解方法(先驗信息已知)、子空間分解方法(先驗信息未知)、常規波束形成、本文方法(先驗信息已知)和本文方法(先驗信息未知)進行500次獨立統計所得目標檢測概率和方位估計的均方根誤差。

圖9 5種方法所得目標檢測概率

圖10 5種方法所得均方根誤差

由圖9仿真結果可知，對于同一目標檢測概率和均方根誤差，子空間分解方法(先驗信息未知)相比子空間分解方法(先驗信息已知)對空間目標檢測和方位估計的穩健性差于2 dB；而子空間分解方法(先驗信息已知)相比本文方法(先驗信息已知)和本文方法(先驗信息未知)對空間目標檢測和方位估計的穩健性差于6 dB以上；而本文方法(先驗信息未知)與本文方法(先驗信息已知)、常規波束形成基本一致；該結果進一步驗證了本文方法采用復域處理，可將一幀時域多個采樣數據轉為多個復域數據，通過多個復域數據累積實現了滿秩協方差矩陣穩定獲取，降低了空間數據穩定性對子空間分解產生的影響；同時通過加權因子αn對各子空間方位譜進行加權處理，在無目標先驗信息情況下，有效提升了空間目標信號子空間方位譜在最終合成方位譜中的比重，進一步降低了背景噪聲對合成方位譜的影響。

3.2 實測數據處理分析

本次處理數據采用圓陣對未知多目標檢測和方位估計試驗所得，相關參數如表2所示。

表2 數據處理參數

本次處理數據環境噪聲級約為70 dB@1 kHz.可視距離內存在多個目標，其中相對圓陣方位10°、30°、60°、90°、220°和270°為噸位較大船只，300°附近有1快速運行快艇，聲級約為120～130 dB@1 kHz。具體處理過程如下：首先對處理數據采用復解析小波變換對1.5～2.0 kHz頻段進行處理；然后對一次處理數據分K=78幀處理(單幀數據為512個采樣數據，幀與幀之間重疊256個采樣數據)，對每幀數據做傅里葉變換分析；最后對各頻點作協方差矩陣估計、特征分分解、方位譜合成。處理中目標先驗信息未知，圖11～圖15分別為子空間分解方法(先驗信息已知)、子空間分解方法(先驗信息未知)常規波束形成、本文方法(先驗信息已知)和本文方法(先驗信息未知)處理所得時間歷程圖。

對比圖11與圖15可知，本文方法所得方位歷程圖顯示目標航跡清晰，目標方位明晰可辨；受空間方位分辨率影響，常規波束形成所得方位歷程圖對220°附近目標顯示效果差于本文方法；受空間數據穩定性影響，子空間分解方法在該時段時間段內無法對10°、30°、60°、90°、220°和270°附近目標實現有效檢測和方位估計，本文方法所得方位譜優于子空間分解方法，進一步驗證了本文方法在無目標先驗信息情況下，通過各子空間峰值索引離散度對各子空間方位譜進行加權處理，進一步降低了背景噪聲對最終合成方位譜影響，相比子空間分解方法有更低的背景噪聲級。

4 結 論

針對基于子空間分解的目標檢測方法穩健性問題，本文提出了一種基于時空瞬時穩定性的方位譜估計方法。該方法依據空間目標信號時域瞬時穩定性，通過復解析變換，將多個時域數據轉換為多個復域數據，通過多個復域數據的累積穩定獲取了滿秩協方差矩陣，降低了空間數據穩定性對子空間分解產生的影響；然后依據各子空間峰值索引離散度差異，對各子空間方位譜進行非線性加權理，降低了背景噪聲對最終合成方位譜影響。數值仿真及實測數據處理結果表明，相比子空間分解方法，在不損失空間分辨率情況下，能夠有效降低空間數據穩定性對協方差矩陣估計產生的影響，在無目標先驗信息情況下，對最低信噪比的需求得到了6 dB以上的降低。