基于優化VMD與改進閾值降噪的滾動軸承早期故障特征提取

陳 鵬, 趙小強,2,3

(1. 蘭州理工大學 電氣工程與信息工程學院， 蘭州 730050; 2. 甘肅省工業過程先進控制重點實驗室, 蘭州 730050) 3. 蘭州理工大學 國家級電氣與控制工程實驗教學中心, 蘭州 730050)

滾動軸承作為旋轉類機械設備的關鍵零部件，其運行狀態直接關系到整個設備的安全狀況[1]。在其旋轉過程中，由于與其它元件接觸摩擦引起損傷，當反復經過損傷點時，采集的振動信號會產生周期性脈沖[2]，該脈沖是判斷滾動軸承發生故障的主要依據。但是軸承的運行環境復雜，常受到傳輸路徑和強噪聲的干擾，導致早期故障的微弱信號淹沒在噪聲中而難以提取[3]。因此，如何有效地分析滾動軸承振動信號，提取出故障引起的沖擊特征進行故障辨識是整個故障診斷的關鍵。

對于滾動軸承的振動信號分析而言，應用信號處理方法對振動信號進行降噪的意義是顯而易見的。近年來，在小波降噪的基礎上，學者們提出了許多自適應信號處理降噪方法，并應用于滾動軸承的故障特征提取[4]。如經驗模態分解(empirical mode decomposition，EMD)[5]、集總經驗模態分解(ensemble empirical mode decomposition， EEMD)[6]、互補集合經驗模態分解(complete ensemble empirical mode decomposition,CEEMD)[7]、局部均值分解(local mean decomposition,LMD)[8]、局部特征尺度分解(local characteristic-scale decomposition， LCD)[9]和固有時間尺度分解(intrinsic time-scale decomposition，ITD)[10]等。這些方法都在不同程度上實現了滾動軸承振動信號的降噪，但是這些方法都是基于遞歸分解原理，沒有從本質上解決其模態混疊和端點效應的缺點。而Dragomiretskiy等[11]提出了一種新的信號自適應分解方法——變分模態分解(variational modal decomposition, VMD)。由于其通過引入變分約束來實現信號的分解，克服了上述方法存在的模態混疊和端點效應問題，被廣泛應用于旋轉機械的振動信號降噪[12]。然而VMD存在模態分解個數k和二次罰因子α需要進行預設置且不同參數值對于分解效果影響大的問題。對于此問題，如通過手動調節較難獲得最優參數。因此，如何自適應地實現VMD最優參數選擇，對于信號的分解效果和后續特征提取至關重要。對此，王奉濤等[13]提出了基于能量的模態個數k選擇；Lian等[14]提出了預設置k的范圍，在設置的范圍內分解信號，計算不同分解模態個數下的能量損失來獲得最佳k。兩位學者采取預設一定的范圍值，對k進行了優化，自適應性不夠。唐貴基等[15]利用粒子群優化算法優化組合參數，建立了基于最小包絡熵的適應度函數；劉建昌等[16]詳細分析了組合參數對VMD分解效果的影響，并通過遺傳變異粒子群算法對其進行優化，適應度函數采用了唐貴基等人提出的最小包絡熵；Yan等[17]提出了基于最小包絡熵的CSA優化VMD分解方法。學者們通過智能優化算法實現VMD組合參數的自適應選擇，建立了能夠表征信號稀疏性的包絡熵適應度函數，實現了信號的分解降噪?？梢?，通過選擇全局和局部搜索能力較強的優化算法，建立合理的適應度函數，可實現VMD參數的自適應選擇分解降噪而獲得較好的效果。

Mirjalili等[18]在2016年提出了WOA算法，證明具有較強的局部和全局搜索能力。峭度由于可以檢測脈沖的瞬變性而應用于選擇模態分量，但是對異常噪聲敏感、穩定性不高。L-峭度[19]是一種描述信號分布特性的指標，是不同階次統計的線性組合，相比峭度只是樣本的四階統計量而言，穩定性更高，能夠消除異常值和噪聲信號的影響，可以更好的檢測周期性脈沖[20]。相關系數可以表達模態分量和原始信號的相關性，但對噪聲敏感。

基于以上分析，本文構建L-峭度與相關系數的自適應度函數，利用WOA優化VMD參數實現振動信號的自適分解降噪，通過構建的準則選取最優模態分量，再通過改進閾值降噪技術對選取的最優模態分量進行進一步降噪，實現振動信號故障特征的有效提取和故障辨識。

1 VMD算法

VMD的本質是通過迭代搜尋變分模型，把信號x(t)分解為具有一定稀疏性的k個模態分量，每個模態分量以中心頻率ωk進行分解，最終得到約束變分問題為

(1)

式中:{uk}={u1,…,uk}為分解后的k個模態分量；{ωk}={ω1,…,ωk}為分解后每個模態分量的頻率中心。為了求解式(1)，利用二次罰函數項和Lagrange乘子將式(1)轉化為如下形式的無約束問題

L({uk},{ωk},λ)=

(2)

式中:α為懲罰因子；λ(t)為Lagrange乘子。

(3)

VMD的具體實現過程如下：

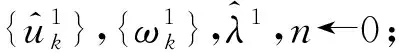
步驟2重復n←n+1；

(4)

更新ωk

(5)

對于所有ω，雙上升步長

(6)

直至滿足迭代終止條件

(7)

式中,ε為判別精度，ε>0。

2 優化VMD參數與改進閾值降噪

2.1 構建L-峭度和相關系數準則

傳統的均值、偏差和峭度等統計量被用于選擇有效模態，這些統計量識別異常的方法只是剔除標準差和均值之間偏離甚遠的數據，這對于小樣本數據而言是不準確的，而恰恰旋轉機械設備的故障數據都屬于小樣本數據，因此常用的以上統計量影響樣本數據統計的正確性。而L-峭度是一種描述信號分布特性的指標，是不同階次統計的線性組合，相比峭度只是樣本的四階統計量而言，穩定性更高，能夠消除異常值和噪聲信號的影響，可以用來很好地確定最佳模態分量。L-峭度的表達式為式(8)

(8)

如果信號的分布形狀扁平，則λ2的值將趨于很大的值，這意味著分布發散，其與標準偏差表征一致，而L-峭度將成為一個很小的值，反之亦然。此外，L-峭度值也由λ4確定，它可以衡量兩個極值(即EX4:4-EX1:4)和兩個中心值(即EX3：4-EX2：4)之間的距離。如果分布是平坦的，則信號分布通常是均勻的，并且λ4接近于零。另一方面，如果分布具有尖峰態，則兩個極值之間的距離通常較大，而兩個中心值之間的距離較小，且λ4較大。因此，L-峭度，也可以代表分布特征。

同時，相關系數的表達式為(9)，其可以表征分解后模態分量與原始信號的相關程度，但對噪聲敏感。

(9)

因此，考慮兩者的優點構建L-峭度和相關系數的適應度函數如式(10)，該適應度函數具備篩選出與原始信號相關性最大的分量和能夠穩定檢測信號中周期性故障脈沖并有效消除噪聲干擾的能力。

fitness=LKCI=(LKI·CI)max

(10)

2.2 WOA優化VMD

設初始最優位置為當前獵物的位置，其它獵物在最初以該位置目標進行移動，并不斷利用式(11)和(12)更新位置

D=|C·X*(t)-X(t)|

(11)

X(t+1)=X*(t)-A·D

(12)

A=2a·rand-a

(13)

C=2·rand

(14)

式中：rand表示產生的[0,1]之間隨機數，隨著循環迭代的增加，a作為收縮因子將從2線性減小到0，其表達式為

a=(2-2t/Tmax)

(15)

式中，Tmax表示設置的最大運行迭代次數。鯨魚通過式(13)和(14)來實現獵物搜索過程中包圍區域的不斷縮小。同時，每個鯨魚又通過螺旋式來更新其與目標位置的距離，其模擬螺旋式更新的數學模型可以表示為如下

X(t+1)=D′·ebl·cos(2πl)+X*(t)

(16)

式中：D′=|X*(t)-X(t)|表示第i只鯨魚和當前最優位置之間的距離；b為常量系數，通常為b=1;l為[1,-1]之間的隨機數。

為了收縮包圍和螺旋更新同步進行，通過概率實現對兩種方式的選擇更新，其數學表達式如下

(17)

當|A|≥1時，將隨機選擇鯨魚遠離當前最優鯨魚來尋找最優的鯨魚，可以提高算法的全局搜索能力，該數學表達式如下

D=|C·Xrand-X(t)|

(18)

X(t+1)=Xrand-A·D

(19)

式中：Xrand表示隨機選取鯨魚的位置向量。

通過WOA對VMD的參數k和α進行組合優化，如圖1所示。其步驟如下

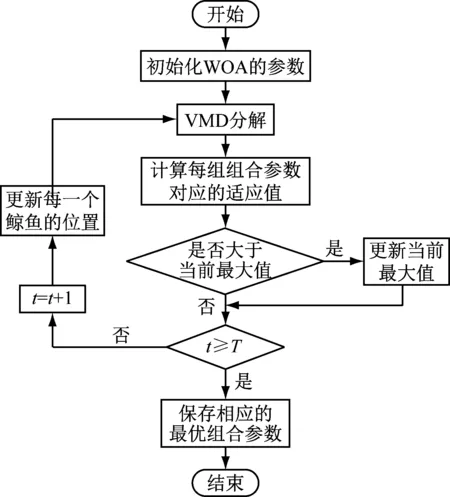
圖1 WOA優化VMD流程

(1) WOA初始化參數k和α的取值范圍為k=[2,15]，α=[200,8 000]以避免不完整的信號分解。

(2) 對振動信號進行VMD分解。

(3) 計算每個組合參數對應位置的適應度值。更新適應度值大于當前值時的最佳適應值。

(4) 確定是否終止迭代。如果t小于Tmax，讓t=t+ 1，并且鯨魚的位置會更新。否則，迭代終止，并保存最佳參數。

2.3 改進閾值算法

硬閾值和軟閾值是常用的降噪技術，在各種應用中得到了廣泛應用[21]，其數學表達式分別為式(20)和(21)

(20)

(21)

(22)

式中：ki是通過試驗設定;σi是第i分量的噪聲標準偏差；N是信號的長度。噪聲標準偏差通過式(23)獲得

(23)

硬閾值函數在閾值處是不連續的，會產生嚴重的波動。在軟閾值函數中，不連續問題得到了解決，但該函數在閾值位置是不可微的，這將導致對于隨機噪聲信號不能準確地估計。在本文中，引用改進的閾值降噪[22]公式為

(24)

其中u=α(|ci(t)|-λi),0<αandμ≤1。

在式(24)中，當α接近0時，閾值式(24)中的函數具有硬閾值函數功能，當α接近1時，則該閾值函數的功能接近于軟閾值功能?？梢?，該函數具有一定的靈活性，參數α一般設置為0.05。

3 設計的故障特征提取方法步驟

滾動軸承運行工況復雜、環境噪聲污染大導致早期故障信號中的故障特征難以提取。本文構建基于L-峭度和相關系數準則，利用WOA優化VMD參數實現振動信號的自適應分解降噪，再選取模態分量中噪聲信息少且與原始信號最大相關的信號進行改進閾值降噪，突出故障特征頻率。其故障特征提取步驟如圖2所示。

圖2 故障提取步驟

(1) 對采集得到的振動信號進行WOA優化VMD自適應分解；

(2) 計算分解之后各分量的LKCI指標；

(3) 選擇最大LKCI指標分量并對最大指標分量進行改進閾值降噪；

(4) 對降噪后的信號進行希爾伯特分析，獲得故障特征頻率。

4 試驗驗證

4.1 試驗1

為了驗證所提故障特征提取方法的準確性和有效性，構建一組周期性脈沖序列信號并添加高斯白噪聲，其仿真信號模型如下

y(t)=s(t)+n(t)

(25)

式中：s(t)為模擬故障沖擊的周期性沖擊分量;位移常數A0=0.6;阻尼系數g=0.04;重復周期T=0.01 s;固有頻率fn=4 000 Hz;采樣點數N=4 096;采樣頻率為20 kHZ;n(t)為高斯白噪聲。產生的周期性沖擊信號如圖3所示，對該沖擊性信號進行加噪獲得強噪聲干擾的混合仿真信號如圖4所示。

圖3 周期性沖擊信號

圖4 仿真信號波形

對仿真信號進行直接包絡如圖5所示，可見在頻率500～1 000 Hz，故障特征頻率出現了模糊，其余特征頻率被噪聲淹沒而沒有得到突出。再對仿真信號按照本文建立的適應度函數，通過WOA優化VMD進行分解，然后進行Teager能量算子解調得到結果如圖6所示。其中Teager能量算子解調相比直接對信號進行包絡的故障特征更加明顯，但在頻率800～1 000 Hz之間出現了故障特征淹沒。繼續通過建立最小包絡熵適應度函數，采用WOA優化VMD分解得到包絡熵最小的最佳模態分量，然后進行改進閾值降噪，得到包絡分析結果如圖7所示，顯而易見其故障特征頻率和其它噪聲頻率相混合而不易觀察，診斷結果較差。最后，應用本文所提出的方法對仿真故障振動信號進行分析如圖8所示，從中可以明顯的看見所有故障特征頻率都得以突出，取得了較好的效果。由上述分析可見，本文所提出方法的可行性和優越性。

圖5 仿真信號包絡

圖6 Teager能量算子

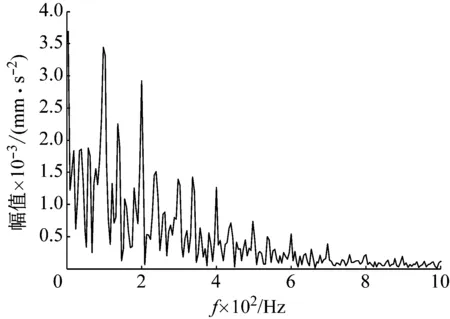
圖7 包絡熵優化

圖8 本文方法故障特征提取

4.2 試驗2

工程試驗數據選擇來自美國西儲大學軸承試驗中心在6205-2RSJEMSKF型深溝球滾動軸承上采集的振動加速度信號，該軸承上的損傷故障采用電火花加工技術設置。本文以故障直徑為0.018 mm、負載為0、轉速為1 730 r/min來模擬滾動軸承的早期微弱故障。在采樣頻率為12 kHZ下進行軸承的加速度信號采集。由滾動軸承的故障特征計算理論，可以計算得到內圈故障特征頻率fi=156.1 Hz、外圈故障特征頻率fo=103.4 Hz、轉頻為Fr=29.95 Hz。首先，對內圈進行故障特征提取，其內圈的加速度振動信號時域圖如圖9所示。

圖9 內圈振動信號時域波形

對內圈振動信號應用本文建立的適應度函數通過WOA優化VMD進行分解，其WOA優化VMD的迭代曲線如圖10所示。

圖10 WOA優化VMD

根據最優組合參數進行VMD分解，得到分解后的IMF分量如圖11所示。

(a) IMF1

其中兩個IMF分量的LKCI值如圖12所示。

圖12 IMF分量的LKCI值

選擇最優的IMF2分量進行Teager能量算子解調如圖13 所示，可見轉頻、故障特征頻率的1倍頻和2倍頻較為突出，3倍頻已較弱。為了進一步對比分析本文方法的有效性，以最小包絡熵為自適應度函數，建立WOA優化VMD選取最佳模態分量，通過改進閾值降噪技術進行降噪得到最后的結果如圖14所示，從圖14中可以看到只有轉頻特征較突出，對于故障特征頻率和2倍頻實現了較微弱的識別，其余倍頻都沒有得到有效的識別。最后，通過本文提出的方法進行分析，其中設定改進閾值降噪中的ki=0.3，得到結果如圖15所示。由圖15可見，內圈故障特征頻率以及2倍、3倍和4倍頻得到了顯著的突出，清楚的判斷出屬于內圈故障。綜上所分析，本文提出的方法得到了較優的特征提取效果。

圖13 Teager能量算子

圖14 包絡熵優化

圖15 本文方法故障特征提取

對外圈進行故障特征提取分析，外圈故障振動信號的時域波形如圖16所示。同理，應用本文建立的適應度函數，采用WOA優化VMD進行分解，然后進行Teager能量算子解調如圖17所示，可以觀察到1倍頻到4倍頻得到突出，但在高頻部分的故障特診頻率被淹沒而難以辨識。其次，建立最小包絡熵適應度函數，采用WOA優化VMD后分解后，選取最佳模態分量進行改進閾值降噪后的結果如圖18所示，可以觀察到較微弱的1倍頻和2倍頻故障特征頻率，特征提取效果較差。

圖16 外圈振動信號

圖17 Teager能量算子

圖18 包絡熵優化

最后，通過本文所提的方法進行分析，其結果如圖19所示，故障特征頻率在低頻和高頻部分都明顯突出，提取效果更佳。

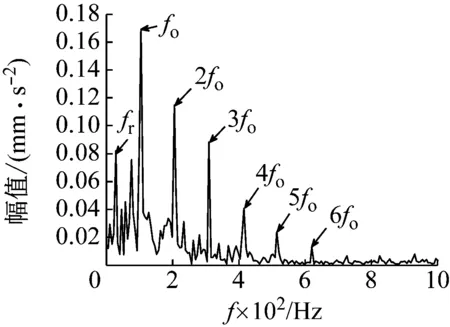
圖19 本文方法故障特征提取

5 結論

針對復雜工況和強背景噪聲干擾下，滾動軸承早期故障信號微弱而故障特征頻率難以提取的問題，提出了優化VMD與改進閾值降噪的滾動軸承故障特征提取方法，主要結論如下：

(1) 該方法對VMD組合參數進行了優化，建立了L-峭度和相關系數的最優模態分量選取準則，結合改進的閾值降噪對選取的最佳分量進行進一步的降噪，實現了故障特征頻率的有效提取，通過仿真和工程數據集驗證了有效性。

(2) 通過WOA優化VMD對故障信號進行降噪，其建立的L-峭度和相關系數準則能夠最大限度保留故障信息和去除噪聲干擾。并通過與最小包絡熵的準則優化結合改進閾值降噪方法進行了對比分析，驗證了提出準則的優越性。

(3) 通過希爾伯特分析表明，相比于WOA優化VMD降噪方法結合Teager能量算子的故障特征提取方法，本文方法降噪后的故障特征更加突出，具有明顯優勢。