換流變閥側套管振動模態及其法蘭根部應力研究

趙莉華, 蔡維哲, 黃小龍, 任俊文, 賈利川, 王 仲

(四川大學 電氣工程學院， 成都 610065)

高壓直流輸電技術因自身低造價、高可靠性優勢，已成為我國輸電系統的關鍵組成部分，而換流變壓器作為連接交流系統與直流系統的關鍵設備，其部件的損壞會直接影響系統的正常運行。作為支持換流變壓器穩定運行的核心元件，套管保證了換流變壓器進出線的絕緣并避免環境對導電桿造成損傷。換流變壓器閥側直流套管常采用干式復合絕緣(RIP)套管，該套管以銅/鋁管為導電桿，環氧樹脂浸紙電容芯子為主絕緣，空氣側采用硅橡膠外護套作為外絕緣，主絕緣與外絕緣之間填充SF6氣體，油側套管插入變壓器油中[1]。這種干式套管的絕緣性能和阻燃性能相對優于油紙式絕緣套管，更適合用于高絕緣裕度要求的高壓直流輸電環境[2]，復合材料套管的抗拉、抗彎性能也優于傳統的瓷套管[3]。

換流變壓器閥側套管通過安裝法蘭固定在變壓器油箱的升高座上，如圖1所示。安裝法蘭作為套管連接部位，同時也是套管結構的薄弱部位。工作狀態下，換流變壓器的繞組和鐵心會周期性振動，這種振動會傳導給閥側套管，使閥側套管受到振動載荷作用，相關研究測得換流變壓器表面振動信號最大主頻幅值約為1.9g、主要頻率集中在100～400 Hz[4]。安裝法蘭承受著套管自重和變壓器振動等復雜環境動力，在長期交變應力作用下易在局部高應力區出現細微裂紋，再由微小裂紋逐步擴展，最終出現疲勞破壞，造成換流變壓器停運和巨大經濟損失。

圖1 閥側套管安裝位置

實際工程中已出現多起閥側套管法蘭根部開裂導致絕緣氣體泄漏事故，某換流站于2016年發生類似事故，檢測后發現多支套管法蘭根部與金屬筒連接拐角處存在不同程度開裂，表面裂紋如圖 2(a)所示。對故障套管拆解后發現，裂縫起始于法蘭外側拐角處，并向內朝著內側密封槽延伸如圖 2(b)所示，裂口存在三個區域：裂紋源、拓展區和瞬斷區。這些套管均已使用多年，經分析認為其開裂符合疲勞斷裂特征，很可能是長年運行下變壓器振動導致金屬法蘭疲勞斷裂。這些裂縫會導致絕緣氣體泄漏，而套管內一定壓力的SF6絕緣氣體對套管起著絕緣保護的作用。當絕緣氣體泄漏到一定程度，套管的絕緣性能會嚴重下降，套管內部發生放電事故，進而危及換流變壓器本體的安全。換流變壓器通常為超高壓或特高壓設備，單臺價值數千萬元以上，一旦因絕緣氣體泄漏而損壞則會造成巨額損失。

(a) 套管表面裂紋

結構發生疲勞破壞的主要原因是應力集中，即結構在形狀突變位置出現應力局部增大的現象。大量試驗研究和理論分析表明，應力集中的部位容易形成疲勞源，在交變載荷的作用下首先萌生裂紋并逐漸延伸，降低結構的疲勞強度[5]。相關研究通常使用結構材料最大局部應力與整體名義應力的比值來描述應力集中，即理論應力集中系數KT，該參數與描述疲勞強度降低程度的缺口疲勞系數Kf呈正相關并在多數情況下服從線性關系[6-7]。理論應力集中系數KT僅與結構形狀相關并可以通過有限元方法計算得到,因此有必要對套管的機械特性及法蘭根部應力分布進行研究，了解其應力集中情況。

目前對套管機械特性的分析多見于變壓器抗震研究領域，研究者通過仿真與試驗的方法研究變壓器套管機械特性，建立套管的簡化有限元模型并分析了其模態特征和模擬地震激勵下的響應特性[8-9]。不過相關研究主要關注地震波短期作用過程中套管整體響應特性和抗震強度，沒有專門對套管法蘭進行詳細分析。此外,文獻[10]根據相關規范要求，對400 kV直流套管受彎曲、扭轉試驗載荷時位移和應力進行了簡單仿真，驗證規范試驗條件下套管應力不超過材料斷裂應力。文獻[11]針對GIS用空心復合套管進行有限元建模，分析了法蘭壁厚、加強筋寬度和膠裝比對機械強度的影響。文獻[12]則針對空心復合套管的鑄鋁帶筋法蘭盤進行仿真分析，得到彎矩載荷下法蘭盤厚度最優設計為20 mm。綜上所述，現有研究對套管法蘭根部應力的分析并不十分充分。

為減少金屬法蘭根部應力集中、降低換流變壓器閥側套管法蘭開裂事故發生概率，本文參考實際套管建立閥側套管有限元模型進行仿真分析，對不同法蘭根部結構的套管施加重力載荷并分析其應力分布特征，研究法蘭根部結構對應力分布的影響；在套管模態分析基礎上采用響應譜方法分析模擬基座振動載荷下法蘭根部應力分布特征，研究振動載荷對應力分布的影響。

1 模態與響應譜分析基本原理

1.1 模態分析基本原理

通過模態分析，可以得到閥側套管的振動特性，即固有頻率和振型。將閥側套管視為一個多自由度系統，其運動微分方程為

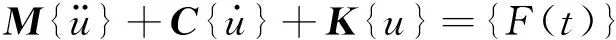
(1)

式中：M、C、K分別為套管的質量矩陣、阻尼矩陣和剛度矩陣;{u}和{F(t)}分別為位移向量和激勵力向量。

若激勵力為0，并忽略系統阻尼的作用，可以得到無阻尼自由振動的運動方程

(2)

該方程的解，也就是套管每個質點的位移可以表現為正弦形式

{u(t)}={φ}sin(ωt+φ)

(3)

將式(3)代入式(2)，可以得到：

(K-ω2M){φ}={0}

(4)

其對應的特征方程為

|K-ω2M|=0

(5)

由于M和K均是正定或半正定矩陣，則式(5)的全部根都是正實數或0，這些根是上述方程特征值，也就是套管的固有頻率。

通過特征方程得到階固有頻率ωi后，將其帶回式(4)，可以得到ωi對應的特征向量，也就是套管的i階振型列向量{φi}。通過模態分析得到固有頻率和振型后可以采用模態疊加方法將實際位移分解為各階模態的線性組合[13]。

1.2 響應譜分析基本原理

響應譜分析方法是一種特殊的模態疊加方法，通過激勵的響應譜和結構的模態進行疊加合并來計算結構承受隨時間變化載荷過程中的響應峰值[14]。響應譜分析將基座激勵載荷施加到具有不同固有頻率和阻尼比的單自由度模型上，得到這些模型的響應峰值與模型固有頻率之間的關系即為該激勵的響應譜[15]。

(6)

在支撐點固定的情況下進行模態分析得到模態矩陣φ，所有特征模態在支撐點處位移為0，因此這些特征模態表示相對位移。將系統各點相對位移用模態疊加表示為{u}=φq，代入運動方程并左乘φT得到

(7)

由于φTMφ,φTKφ是對角矩陣，阻尼也可以表示為對角矩陣，所以可以將方程組(7)解耦得到如下解耦模態方程

(8)

將支撐運動沿三個正交方向分解

b(t)=bx(t)lx+by(t)ly+bz(t)lz

(9)

矢量lx對所有x方向平動自由度來說，值均為“1”，對所有其他自由度則均為“0”，矢量ly、lz同理。由此得到模態運動方程

(10)

因此，當已得到通過基座運動施加的k方向激勵載荷的響應譜時，系統階模態的響應峰值振幅是相應固有頻率下的響應譜值與參與因子(結構屬性，與載荷無關)的乘積。

Rkj=Sd(ωj,ζj,bk(t))Γkj

(11)

得到各階模態的響應值后，為了獲得總的響應值，需要將各階模態響應值按一定的方法進行合并。對固有頻率分布比較均勻的結構，可以采用各階模態響應的平方和的均方根作為總響應(SRSS方法)；對固有頻率分布存在集中，即各階模態具有關聯耦合性的結構，則需要采用完全二次方合并方法(CQC方法)進行疊加[16]。

2 換流變閥側套管模型

2.1 閥側套管有限元模型

本文根據某500 kV換流變壓器閥側復合套管進行實體建模得到有限元模型如圖 3所示，模型主要由導電桿、套管本體、金屬法蘭三部分組成，忽略均壓環、接線端子等附屬結構。套管全長7 900 mm，空氣側套管長6 100 mm，油側套管長1 800 mm，套管外徑350 mm，金屬法蘭及套筒長1 100 mm。套管各部分材料和計算采用的材料機械性能參數如表1所示，復合材料套管本體僅考慮玻璃鋼彈性模量20 GPa，并采用考慮其外部包裹硅橡膠傘裙的等效密度，取7 000 kg/m3。取套管整體結構阻尼比為2%，設定套管安裝角度為相對水平面30°向上，通過法蘭盤靠近油側面固定在變壓器上，忽略法蘭盤上的螺栓。以套管軸線在水平面上投影為x軸方向、豎直方向為y軸方向建立坐標系。

圖3 閥側套管模型示意圖

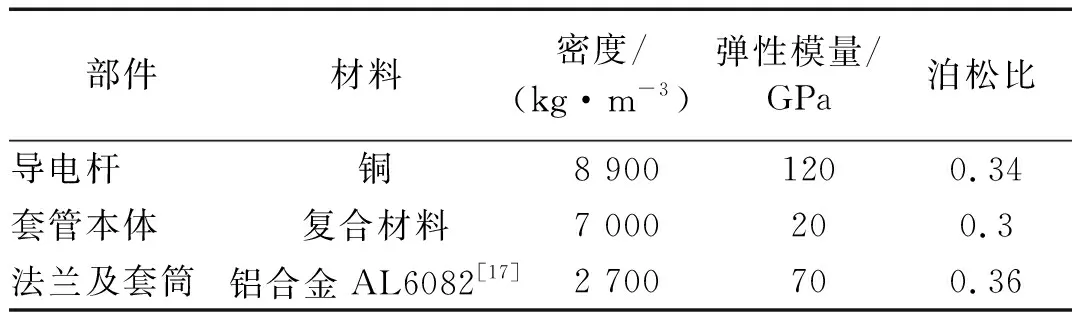
表1 各部件材料機械性能

2.2 套管根部結構

為了解套管根部結構對套管整體變形和金屬法蘭上應力分布的影響，將法蘭拐角的曲率半徑和套筒上加強筋的長度、寬度、高度、起始位置作為變量，觀察其改變時套管整體變形和法蘭應力分布的變化。

法蘭套筒上常設置加強筋以增加結構剛度，但受套筒上末屏盒子等結構的限制，僅能在套筒的上下兩側設置長條形加長筋。根據該加強筋可以將套管根部結構劃分無加強筋、加強筋未與法蘭盤連接、加強與法蘭盤連接三種狀態，如圖 4所示。將套筒中截面上加強筋與套筒連接位置到法蘭盤的距離定義為加強筋的起始位置，從該位置起計算加強筋的長度，將中截面上加強筋頂部到套筒圓柱面的距離定義為加強筋的高度，將加強筋兩個側面間距離定義為加強筋的寬度，從而得到長條加強筋長度、寬度、高度、起始位置四個變量，如圖 5(a)、(b)、(c)所示。如圖 5(d)所示，法蘭拐角是法蘭盤與套筒之間過渡的連接拐角，作為結構的尺寸突變位置，該位置會用圓角過渡以均勻應力，其曲率半徑是影響套管根部應力分布的關鍵參數。

(a) 無加強筋

(a) 法蘭及套筒側視圖(加強筋未連接)

除長條加強筋外，法蘭盤上還可以設置三角形加強筋連接在法蘭盤和套筒之間，三角形加強筋在長條加強筋兩邊對稱分布，如圖 6(a)所示。將三角形加強筋和套筒中截面的夾角定義為三角形加強筋的安裝角度，如圖 6(b)所示。設置三種排列方式，即法蘭盤平面的每個象限有1、2、3條三角形加強筋，三角形加強筋之間的夾角與安裝角度相等，并定義離中截面最遠的三角形加強筋與中截面的夾角為最大加強筋角度，如圖 6(c)、(d)所示。

(a) 三角形加強筋示意

3 套管根部應力靜力仿真

3.1 拐角曲率半徑的影響

對閥側套管受重力載荷，法蘭拐角曲率半徑從1 mm增加到20 mm條件下計算金屬法蘭的應力和套管整體變形。曲率半徑為2 mm時金屬法蘭等效應力分布如圖 7(a)、(b)所示，應力主要集中在法蘭拐角環面的頂部和底部。法蘭拐角最大等效應力值和套管整體最大變形曲線如圖 8所示，隨著拐角曲率半徑從1 mm增加10 mm，最大變形值在均值39.44 mm的0.4%范圍內輕微波動；最大等效應力值迅速減小并趨于平緩，當曲率半徑為6 mm時等效應力減小到最大值的50%，當曲率半徑增大到20 mm時等效應力減小到最大值的35%。

圖7 法蘭及套筒應力分布(曲率半徑為2 mm)

圖8 最大應力與最大變形隨拐角曲率半徑變化曲線

3.2 加強筋長度的影響

對閥側套管受重力載荷，長條加強筋末端連接法蘭盤和不連接法蘭盤兩種情況下，將加強筋長度從100mm增加到900 mm，計算金屬法蘭的應力和整體變形。法蘭拐角最大等效應力和套管整體最大變形曲線如圖 9所示，可以看出加強筋末端與法蘭盤連接狀態下，最大變形和等效應力都明顯小于未連接狀態，連接狀態最大應力均值為86.9 MPa，相比不連接狀態下最大應力均值104.7 MPa減小了17%。當加強筋長度從100 mm增加到900 mm，法蘭拐角最大應力值在一定范圍內輕微波動，未連接狀態下波動范圍為均值的4.4%范圍，連接狀態下波動范圍為均值的3.1%；套管最大變形值隨加強筋長度增加以近似線性規律下降，未連接狀態下降了2.1%，連接狀態下降了1.4%。

圖9 最大應力與最大變形隨加強筋長度變化曲線

3.3 加強筋寬度的影響

對閥側套管受重力載荷，加強筋末端連接法蘭盤和不連接法蘭盤兩種情況下，將加強筋寬度從10 mm增加到100 mm，計算金屬法蘭的應力和整體變形。法蘭拐角最大等效應力和套管整體最大變形隨加強筋寬度變化曲線如圖 10所示，可以看出當加強筋末端與法蘭盤連接，法蘭拐角的應力和套管變形均明顯小于加強筋未連接狀態。當加強筋寬度從10 mm增加到100 mm，除加強筋未連接狀態下法蘭最大應力緩慢增加了5.04%；加強筋連接狀態下法蘭拐角最大應力和兩狀態下的套管最大變形均明顯下降，連接狀態下最大應力下降了56%，非連接狀態和連接狀態下最大變形值分別下降了17.5%和27.8%。

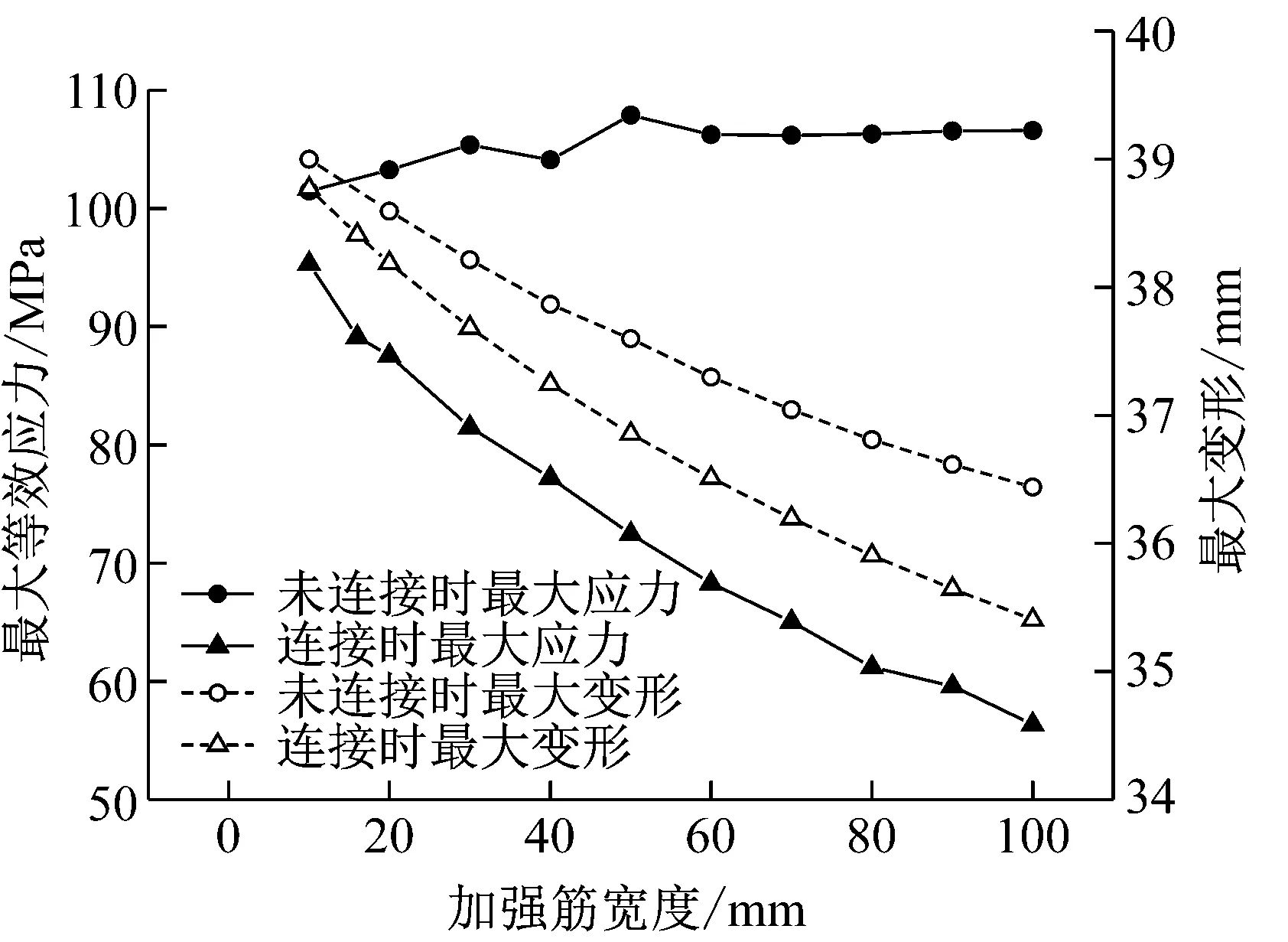
圖10 最大應力與最大變形隨加強筋寬度變化曲線

3.4 加強筋高度的影響

對閥側套管受重力載荷，加強筋末端連接法蘭盤狀態下將加強筋高度從50 mm增加到100 mm，加強筋不連接法蘭盤狀態下將加強筋高度從10 mm增加到100 mm，計算金屬法蘭的應力和套管整體變形。法蘭拐角最大等效應力和套管整體最大變形隨加強筋高度變化曲線如圖 11所示，當加強筋高度<70 mm時兩種狀態下套管最大變形相差較小，此后兩條曲線差距逐漸明顯，而連接狀態下法蘭拐角最大應力一直明顯低于未連接狀態。當未連接狀態下加強筋高度從10 mm增加到100 mm，套管最大變形減小了3.6%，法蘭拐角最大應力在均值102.3 MPa的1.8%范圍內輕微波動。當連接狀態下加強筋高度從50 mm增加到100 mm，套管最大變形減小了3%，法蘭拐角最大應力減小了17.9%。

圖11 最大應力與最大變形隨加強筋高度變化曲線

3.5 加強筋起始位置的影響

對閥側套管受重力載荷，加強筋末端連接法蘭盤和不連接法蘭盤兩種情況下，將加強筋起始位置從10 mm增加到100 mm，計算金屬法蘭的應力和套管整體變形。法蘭拐角最大等效應力和套管整體最大變形隨加強筋起始位置變化曲線如圖 12所示，加強筋連接狀態下應力和變形均明顯小于非連接狀態，并且隨著加強筋起始位置遠離法蘭盤，套管最大變形近似線性規律上升，法蘭拐角處最大應力先明顯下降后趨于平緩，兩種狀態下曲線變化規律十分相近。當加強筋起始位置距法蘭盤距離從10 mm增加到100 mm，連接狀態套管最大變形減小了0.12%，非連接狀態套管最大變形減小了0.28%，其變化比例接近加強筋長度變化情況下套管響應的變化；非連接狀態下套管最大應力先隨起始位置增加到50 mm減小到最大值的82.6%后保持平緩，連接狀態下套管最大應力先隨起始位置增加到50 mm減小到最大值的86.7%后保持平緩。

圖12 最大應力與最大變形隨加強筋起始位置變化曲線

3.6 三角形加強筋安裝角度與排列方式的影響

對閥側套管受重力載荷，長條加強筋末端與法蘭盤連接情況，設置三種排列方式的三角形加強筋并調整其安裝角度，計算金屬法蘭的最大應力。不同排列方式下法蘭最大等效應力隨三角形加強筋安裝角度變化曲線如圖 13所示，最大應力值隨安裝角度的增大明顯增加。三角形加強筋排列方式選擇排列1時，隨著安裝角度從10°增加到60°，最大等效應力值增加了25.4%，安裝角度超過60°后排列1曲線接近無三角形加強筋時最大應力值并保持相對平穩；三角形加強筋排列方式選擇排列2時，隨著安裝角度從10°增加到40°，最大應力值增加了36.4%，并且安裝角度大于35°后排列2與排列1的曲線基本重合；三角形加強筋排列方式選擇排列3時，隨著安裝角度從10°增加到27.5°，最大等效應力值增加了34.7%，并且安裝角度大于22.5°后排列3和排列2的曲線基本重合。

圖13 最大應力隨三角形加強筋安裝角度變化曲線

比較三種不同排列方式，可以發現相同安裝角度時三角形加強筋數量多的排列方式最大等效應力值更低，安裝角度為10°時排列三的最大應力值是排列1最大應力值的81.4%。將排列1與排列2同一安裝角度的最大應力值之差作為縱坐標，將排列2下該安裝角度對應的最大加強筋角度作為橫坐標，得到排列1與排列2間的最大應力差曲線，同理可以得到排列2與排列3之間的最大應力差曲線，如圖 14所示。從圖 14可以看出，當最大加強筋角度大于65°時最大應力差約等于0，此時角度最大的加強筋對法蘭最大等效應力幾乎無影響。

圖14 不同三角形加強筋排列方式的最大應力差曲線

4 套管根部應力動力仿真

4.1 套管模態分析

為了解閥側套管的振動機械特性，對套管進行模態分析，仿真計算套管的固有頻率及其對應的振型。在考慮靜態載荷預應力的基礎上，計算閥側套管0～50階模態固有頻率如圖15所示，套管1階固有頻率為2.935 Hz，套管50階固有頻率為733.8 Hz，前10階模態固有頻率在2～80 Hz范圍內。

圖15 閥側套管前50階模態固有頻率

從圖15中可以看出，套管常常每兩階模態固有頻率近似相同、振型相似，區別在于最大振幅位置的振動方向不同。以套管前4階振型為例，套管1、2階模態振型類似于套管頂端受徑向力狀態如圖 16(a)所示，套管向一個方向彎曲變形，越靠近套管頂端振幅越大，兩階振型區別在于1階振型偏向z軸負方向而2階振型偏向z軸正方向。套管3、4階模態振型則如圖 16(b)所示，套管空氣側中部呈拱形，存在套管頂端和空氣側中部兩個振幅較大區域，兩階振型區別在于3階振型頂端偏向y軸負方向而4階振型頂端偏向y軸正方向。

(a) 1階模態振型

換流變壓器振動的主要頻率集中在100～400 Hz，而從圖15中可以看出，套管的13～31階固有頻率處于100～400 Hz范圍內。通過對閥側套管模型進行諧響應分析，得到套管x軸方向位移的幅頻響應曲線如圖17所示，該曲線在100～400 Hz范圍內有數個峰值。這說明從換流變壓器傳來的振動載荷會導致套管位移和應力的明顯變化，在長期振動載荷作用下，安裝法蘭拐角位置逐漸出現細微裂紋，最終導致疲勞破壞并在應力集中部位開裂。

圖17 套管位移幅頻響應曲線

4.2 套管振動載荷響應譜

由于換流變壓器振動信號主要頻率集中在100～400 Hz、最大主頻幅值約為1.9g，本文設置套管所受加速度激勵幅值為2g，振動頻率分別為100、200、300、400 Hz，振動方向分別為x、y、z軸方向，以探究不同振動載荷條件下套管的響應。采用Newmark-β法計算不同固有頻率單自由度模型受激勵時的最大加速度響應值，得到不同振動載荷的加速度響應譜如圖 18所示。因為閥側套管的各階模態具有一定的耦合性，采用CQC方法將套管模態振型與該激勵響應譜值疊加合并得到套管承受基座振動激勵的最大響應。

圖18 振動激勵的絕對加速度響應譜

4.3 振動載荷的影響

通過響應譜方法分析閥側套管受到基座傳來的振動載荷時的最大應力幅值，該載荷振動方向為x、y、z軸方向、振動加速度幅值為2g、振動頻率分別為100 Hz、200 Hz、300 Hz、400 Hz。

振動載荷下套管法蘭的應力依然集中在法蘭拐角位置，如圖 19所示。不同根部結構下法蘭最大應力幅值如圖 20所示，圖(a)、(b)、(c)分別代表法蘭根部結構為無加強筋、長條加強筋未連接和加強筋連接，橫坐標代表不同振動載荷頻率、不同顏色的條形代表不同的振動載荷方向。從圖 20中可以看出，套管響應隨振動頻率增加而減小，振動載荷頻率為100 Hz時法蘭最大應力幅值約為20～22 MPa，高于其余情況。比較套管受不同方向振動時最大應力幅值，發現當振動頻率<400 Hz，套管受x軸向振動響應幅值大于y軸方向大于z軸方向，僅當振動頻率為400 Hz時套管受x軸方向振動響應幅值小于y軸方向。并且當根部結構為加強筋連接時，套管受z向振動和受x、y向振動的最大應力幅值差別相對另外兩種根部結構較小，這是因為加強筋連接結構降低了套管受x、y方向振動時的應力幅值。

圖19 振動載荷下法蘭應力幅值分布

(a) 無加強筋

套管受不同方向振動載荷時法蘭最大應力幅值情況如圖 21所示，圖(a)、(b)、(c)分別代表振動載荷為x、y、z方向，不同顏色條形代表不同法蘭根部結構。從圖 21中可以看出，加強筋未連接結構下法蘭最大應力幅值與無加強筋結構下接近，未連接加強筋對振動載荷下法蘭拐角應力沒有明顯作用；加強筋連接結構下，受x、y方向振動載荷的法蘭最大應力幅值明顯低于無加強筋狀態，但受z方向振動載荷的法蘭最大應力幅值與其余兩種結構類似。連接加強筋結構對x、y方向振動載荷下套管法蘭應力有一定的抑制作用，但對z方向振動載荷下套管法蘭應力沒有明顯影響。

(a) x軸向振動

5 結 論

(1) 閥側套管前10階模態固有頻率在2～80 Hz范圍內，套管的13～31階固有頻率處于100～400 Hz范圍。

(2) 套管受重力載荷時，應力集中在法蘭拐角的頂部和底部，應力隨著拐角曲率半徑的增加而明顯減小并在曲率半徑>10 mm后趨于平緩。

(3) 長條加強筋與法蘭盤連接時能明顯降低法蘭拐角的應力，若不與法蘭盤連接則僅能對套管的變形產生明顯影響；當加強筋與法蘭連接時，增大加強筋的寬度和高度能進一步降低法蘭拐角應力，增加加強筋長度則沒有明顯影響；加強筋的起始位置不能距離法蘭盤過近，否則反而會增大拐角處應力。

(4) 三角形加強筋安裝位置靠近應力集中位置時能明顯降低法蘭拐角處應力，但隨著安裝角度的增大降低應力的能力會減弱，安裝角度>60°后不再有明顯影響。

(5) 套管受基座振動時，應力幅值隨振動頻率升高而降低。與法蘭盤連接的長條加強筋能明顯降低套管受平行于軸線的水平方向振動和受豎直方向振動時的應力幅值，對受垂直于軸線的水平方向振動時套管應力幅值則沒有明顯作用。