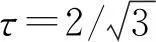自旋-1角動量分量的不確定關系

南 華, 玄東平, 胡曉會

(延邊大學 理學院數學系, 吉林 延吉 133002)

1 引言與預備知識

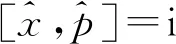
對于兩個可觀測量A和B, Robertson[4]推導出不等式

(1)

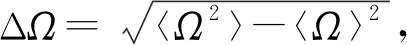
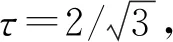
2 乘積形式的不確定關系

自旋角動量是量子系統的可觀測量, 已知自旋-1角動量的三個分量為

且滿足與軌道角動量相同的對易關系：

[Sx,Sy]=i?Sz, [Sy,Sz]=i?Sx, [Sz,Sx]=i?Sy.

(2)

令?=1, 由不確定關系(1)可得

ΔSxΔSy≥|〈Sz〉|/2, ΔSyΔSz≥|〈Sx〉|/2, ΔSzΔSx≥|〈Sy〉|/2,

(3)

因此, 有

(ΔSxΔSyΔSz)2≥|〈Sx〉〈Sy〉〈Sz〉|/8.

(4)

由于式(4)僅在不等式兩端全為0時等號成立, 但沒有實際意義.因此考慮不確定關系

(5)

使式(5)等號成立的τ稱為三方系數, 其作用是使式(5)在兩端非零時可達到下確界, 即不確定關系(5)是緊的.

考慮系統純態的一般形式

通過計算可得

為確定不等式(5)中常數τ的值, 根據

對于0≤θ1,θ2<2π, 0≤α1,α2<π/2, 求得

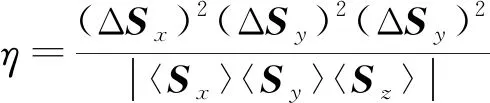
(6)

的最小值.可知當θ1=π/2,θ2=5π/4時, 存在π/5<α1<π/4, π/9<α2<π/8, 使得

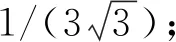
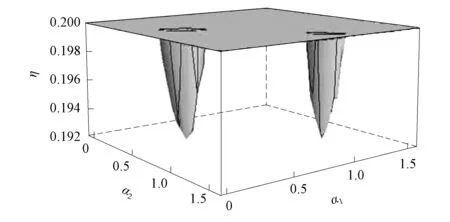
圖1 式(6)最小值的數值解Fig.1 Numerical solution of minimum value of formula (6)

3 和式的不確定關系

下面研究自旋-1角動量的三個分量相關和式的不確定性關系.由式(2)可得

(ΔSx)2+(ΔSy)2≥2ΔSxΔSy≥|〈Sz〉|,

(ΔSy)2+(ΔSz)2≥|〈Sx〉|, (ΔSx)2+(ΔSz)2≥|〈Sy〉|.

(7)

由式(7)可得三個分量的和式不等式

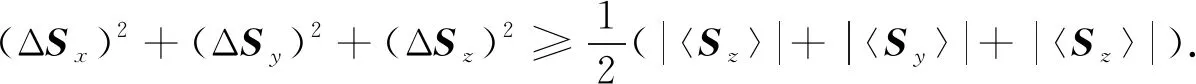
(8)

對于N維系統, 自旋-l時自旋量子數l=(N-1)/2, 且對任意量子態有

由于Sk(k=x,y,z)的期望值定義了一個向量, 其最大長度等于沿任意軸的極值特征值, 因此文獻[16]給出了如下不等式

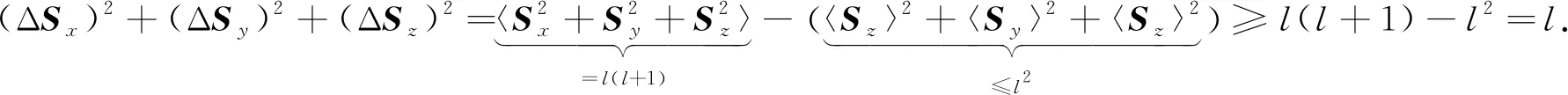
(9)

對一組數據{x1,x2,…,xn}, 已知代數平均值不超過二次平均值, 即

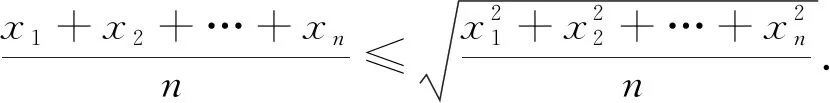
(10)

由此可得

由式(11)可知, 式(8)是非緊的, 因此考慮存在一個常數τ, 使不確定關系

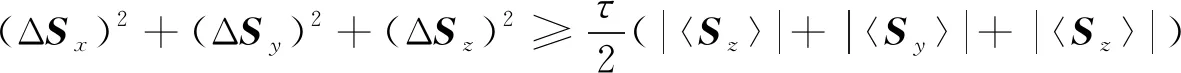
(12)

成為緊的, 即可達到該下確界.

對于0≤θ1,θ2<2π, 0≤α1,α2<π/2, 求得

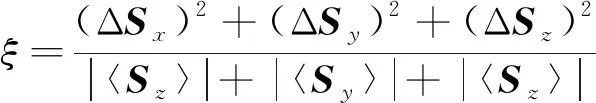
(13)

的最小值.

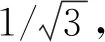
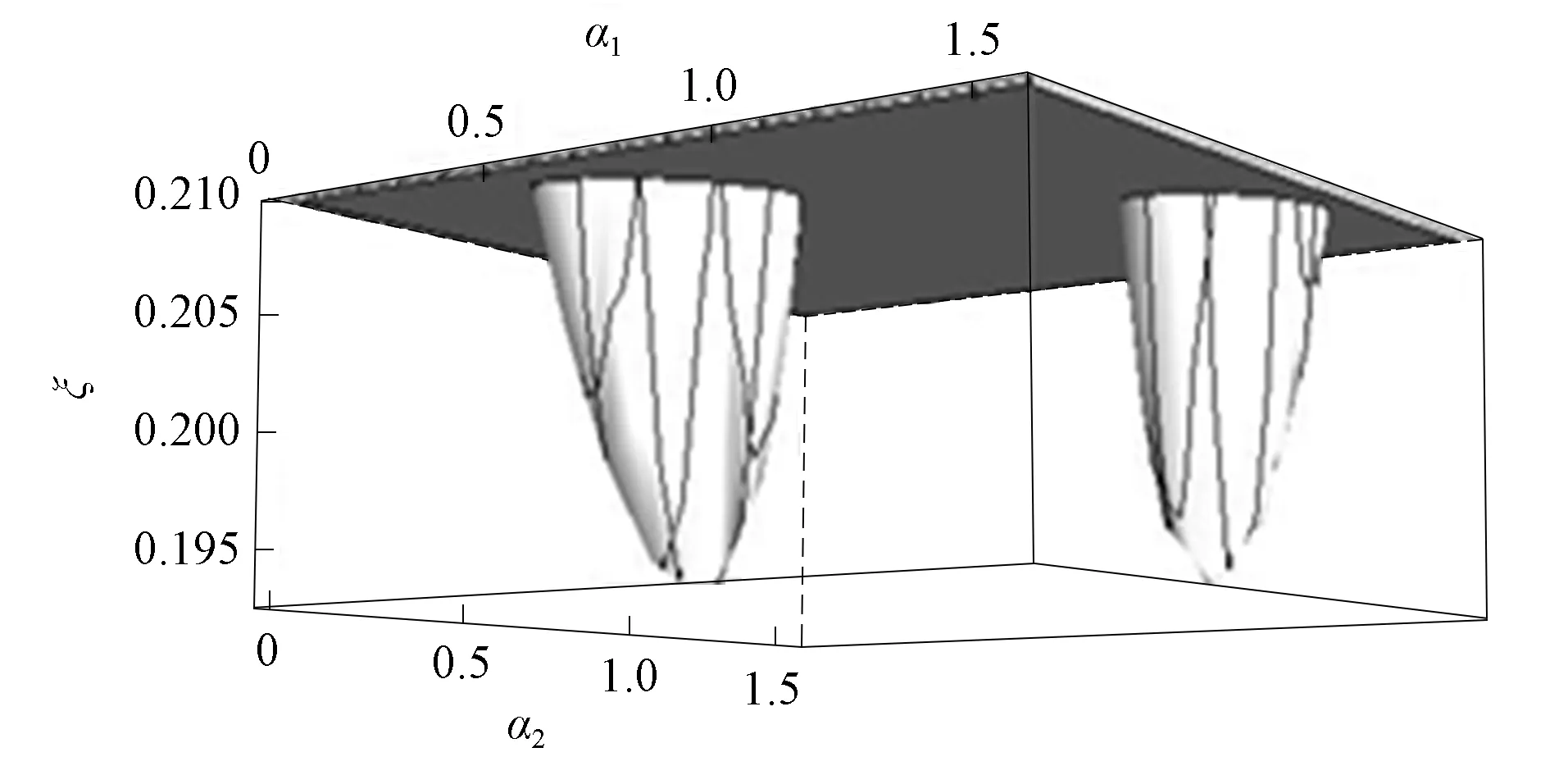
圖2 式(13)最小值的數值解Fig.2 Numerical solution of minimum value of formula (13)