高分子鏈模型對兩親性二嵌段共聚物系統均勻溶液/膠束轉變的影響

張 惠, 韓向剛

(內蒙古科技大學 理學院, 內蒙古 包頭 014010)

在兩親性嵌段共聚物溶液中, 當溫度低于某數值(臨界溫度)時, 系統可形成以疏水嵌段為核心, 親水嵌段為殼層的膠束. 研究表明, 膠束的性質與溶液的濃度、 溫度和高分子鏈模型有關. 目前, 聚合物膠束在藥物輸送[1]、 黏度改性、 膠體與聚合物混合物的穩定化和組織工程學[2-3]等領域應用廣泛.

兩親性嵌段共聚物的理論計算和實驗結果均表明, 在臨界溫度下, 存在一個具有一定寬度的平衡區, 在該區域存在大量的游離聚合物和締合聚合物(如膠束), 在該平衡區上, 溶液體系完全以膠束的形式存在[4-5]. 關于膠束性質的研究結果較多, 但高分子鏈模型的不同行走方式對膠束聚集影響尚未見文獻報道.

理論模擬是研究聚合物相行為的重要方法[6], 其中自洽場理論[7-8]是研究嵌段共聚物自組裝行為最有效的方法之一, 這是因為自洽場理論可表征嵌段共聚物分子鏈的位型、 短程排斥作用和不同組分間的不相容性. 文獻[9-11]用自洽場理論研究了兩親性嵌段共聚物的聚集形態. 本文用格子自洽場方法, 模擬計算嵌段共聚物的選擇性溶液體系的相行為[12-13]及棒/線嵌段共混物的自組裝[14], 并研究高分子鏈模型的不同行走方式(即體積排斥作用的差異)對AB兩親性二嵌段共聚物聚集行為的影響. 結果表明, 溫度是影響體系聚集行為的重要因素.

1 模型與理論

首先描述滿足不可壓縮條件的兩親性二嵌段共聚物溶液的格子自洽場方法. 系統含有np條二嵌段共聚物, 若每條聚合物鏈由Nns個親水鏈段B(表示非黏性單體)和Nst個疏水鏈段A(表示黏性單體)組成, 則聚合物鏈長為N=Nst+Nns[14].體系中格子總格點為NL, 假設A,B單體和溶劑具有相同的尺寸, 且每個單體或溶劑分子均占據一個格點, 從而可得NL=nh+npN.體系中存在的唯一非鍵相互作用是疏水嵌段間最近鄰對的吸引作用-ε(ε>0).近似相互作用能[10]為

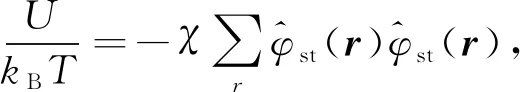
(1)

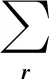
(2)

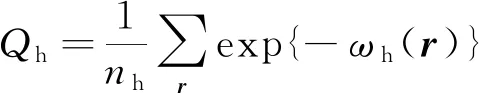
由ω-(r)和ω+(r)使自由能泛函F取得極小值, 可得自洽場方程組為

ω-(r)=2χφst(r),

(3)

φst(r)+φns(r)+φh(r)=1,

(4)

其中

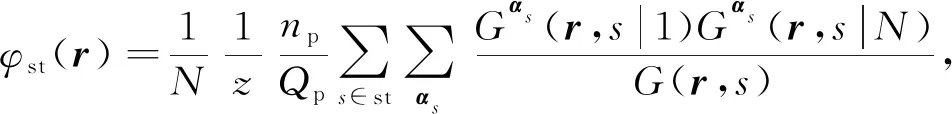
(5)

(6)

(7)

式(5)和式(6)分別表示疏水單體(A鏈段)和親水單體(B鏈段)在r點的平均體積分數, 式(7)表示溶劑分子在r位點的平均體積分數,

Gαs(r,s|1)可通過迭代關系[15]

(8)

計算, 其中

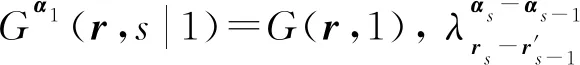
聚合物鏈的另一個末端分布函數Gαs(r,s|N)可利用迭代關系

(9)

計算得到, 對于所有αN值的初始條件為GαN(r,N|N)=G(r,N).

本文用實空間方法求解具有周期性邊界的簡立方格子自洽場方程[16].從適當的隨機場ω-(r)和ω+(r)開始計算, 當連續兩次迭代的自由能F變化達到設定精度時, 即可得鞍點位形.根據不同初值場下鞍點位形的自由能大小確定系統的穩定狀態.

2 結果與討論

兩親性二嵌段共聚物溶液的性質取決于4個因素, 包括Flory-Huggins作用參數、 聚合物的鏈長N(假設N=20)、 疏水嵌段的長度Nst(Nst=4保持不變)和高分子鏈模型.在邊長為40簡立方格子中, 研究高分子濃度、 相互作用參數和高分子鏈模型對均相溶液/膠束轉變的影響, 結果如圖1所示.圖1構建了以作用參數χc和高分子濃度為坐標的相圖, 給出了不同行走方式的分子鏈模型下均勻溶液/膠束轉變溫度(膠束臨界溫度)隨高分子濃度的變化, 其中圓形和正方形分別表示可直接折返和不可直接折返的高分子鏈模型膠束出現時的作用參數.由圖1可見, 隨著高分子濃度的增加, 膠束出現的作用參數χc減小, 即膠束出現的溫度升高[17].在疏水嵌段比例和高分子濃度保持不變的情況下, 當高分子鏈模型為不可直接折返的隨機行走鏈時, 膠束出現的作用參數χc減小.因此， 高分子濃度的增加與不可直接折返的高分子鏈模型均有利于膠束出現.

圖1 兩親性二嵌段共聚物溶液系統相圖Fig.1 Phase diagram for amphiphilic diblock copolymer solutions

膠束核黏性單體平均體積分數可表征膠束的聚集程度, 本文計算了不同高分子濃度條件下膠束核黏性單體平均體積分數隨相對作用參數χr(χr=χ-χc)的變化, 結果如圖2所示, 其中正方形、 三角形、 菱形、 星形分別表示cp=0.1,0.3,0.5,0.8, 空心和實心分別表示可直接折返和不可直接折返的高分子鏈模型.在假設濃度不變的條件下, 膠束核平均聚集程度隨χr的增加而增加, 當相對作用參數足夠大時, 平均聚集程度趨于不變.分子鏈模型對膠束平均聚集程度影響與高分子濃度有關.當cp=0.1時, 不可直接折返的無規行走聚合物鏈與可直接折返的聚合物鏈膠束的平均聚集程度相差很小, 表明在該濃度下, 不同行走方式的高分子鏈模型對膠束形成過程影響很小； 當cp=0.3時, 不同行走方式的高分子鏈模型的膠束核平均聚集程度差別較大, 此時體積排斥效應對膠束形成過程影響最大.當高分子濃度進一步增加時, 不同行走方式的聚合物鏈對膠束長大過程的影響趨于減小.因此, 不可直接回折的隨機行走高分子鏈模型增加了體積排斥效應, 有利于膠束的出現, 但在一定程度上限制了膠束聚集程度的增加.

圖2 不同濃度下膠束聚集程度隨相對作用參數的變化Fig.2 Change of degree of micellar aggregation with relative interaction parameters at different concentrations

比熱峰是表征轉變寬度的重要物理量[18].兩親性AB二嵌段共聚物在每個晶格點的比熱容可表示為(以kB為單位)

在不同鏈模型下, 均勻溶液/膠束轉變的熱容量Cv隨相對作用參數的變化如圖3所示, 其中實心和空心對應不可直接折返和可直接折返的高分子鏈模型, 正方形和三角形分別對應cp=0.1,0.3, 圓形和五角星分別對應cp=0.5,0.8.由圖3可見, 對于較低高分子濃度體系(cp=0.1,0.3), 均勻溶液/膠束發生轉變時, 系統的Cv曲線出現一個相對對稱的比熱峰.不同鏈模型的熱容峰高度不變, 且峰的半高寬(轉變寬度)保持不變.即不同鏈模型熱容峰的對稱性在相同濃度下不發生明顯改變.隨著高分子濃度的增加, 比熱峰的高度降低, 且彼此高度不同, 峰的不對稱性略有下降.當cp=0.5時, 可直接折返的聚合物鏈出現了3個峰值, 與不可直接折返鏈差異明顯.在高濃度(cp=0.8)下, 二者均未出現小的熱容峰, 不可直接折返鏈模型高于可直接折返高分子鏈模型的熱容峰值, 與cp=0.5時的結果完全相反.由熱容曲線和膠束平均聚集程度曲線可見: 當高分子濃度較低(cp=0.3)時, 可直接折返和不可直接折返鏈模型的膠束平均聚集程度的變化相差較大, 但膠束聚集的相對趨勢變化基本相同； 當分子濃度較高時, 其膠束平均聚集程度的變化相對較小, 但膠束聚集的相對趨勢差異明顯, 這是因為不同分子鏈模型引入體積排斥效應的影響與聚合物濃度有關.

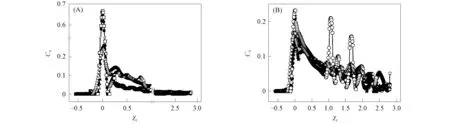
圖3 不同濃度下比熱峰隨相對作用參數χr的變化Fig.3 Change of specific heat peak with relative interaction parameters χr at different concentrations

綜上, 本文用格子自洽場方法模擬了高分子濃度和高分子鏈模型對膠束形成的影響.通過計算體系的相圖和熱容量, 證明了隨著高分子濃度的增加, 出現膠束結構所需的溫度升高.不可直接回折的隨機行走聚合物鏈增加了體積排斥效應, 有利于出現膠束結構, 但也限制了膠束聚集程度的增加, 這種影響與聚合物的濃度有關.