尺寸關聯更改傳播路徑生成方法

楊 波 尚俊芝 馬 寧 高常青

濟南大學機械工程學院，濟南，250022

0 引言

工程更改的傳播會導致開發過程中的復雜性和風險增加、成本提高[1-2]。復雜產品在尺寸、結構等屬性方面往往存在著多尺度的關聯，其中任一屬性發生的設計更改，不僅會觸發相關零件結構上的連鎖關聯更改，而且也會引發相關尺寸參數的一系列變更傳遞。鑒于尺寸更改的廣泛性與復雜性，有必要對其傳播過程進行描述與分析。

目前，針對尺寸更改傳播的研究主要包括尺寸關聯設計和更改傳播路徑兩個方面，兩者存在很強的依賴性。

關聯設計是準確預測更改傳播的關鍵。針對關聯設計中存在的關聯傳遞、關聯耦合等問題，目前的解決方法主要有基于骨架模型的關聯設計方法[3]、基于產品族模塊組合的主從關聯設計方法[4]、基于設計結構矩陣的關聯解耦策略[5]、基于關聯的變更操作算法[6]等。以產品關聯設計理論為基礎，尺寸關聯設計是在參數化設計技術的基礎上，通過建立尺寸約束以及特征參數的多參數關聯關系來完成對變更傳播的影響分析。劉振宇等[7]運用灰熵關聯分析對特征關聯參數進行篩選，研究了多個特征參數關聯對復雜產品性能的影響；徐新勝等[8]采用事物特性表技術，基于尺寸關聯設計模型，實現了產品自頂向下的變型設計；彭翔等[9]通過定性分析設計變量與性能目標間的關聯關系，構建了精確的復雜產品整體性能關聯模型；BAUDOUI等[10]利用后發式局部不確定傳播分析方法，減少了參數不確定性對性能的影響。更改傳播路徑的搜索是尺寸更改傳播研究的重要分支，有效的關聯路徑搜索算法是解決尺寸更改傳播效率問題的重要手段，目前常見的方法主要有基于關聯網絡的方法和基于設計結構矩陣的方法。楊帆等[11-12]建立了基于公式量化表達的產品參數關聯網絡模型，研究了更改傳播路徑的搜索算法；MA等[13]通過在參量關聯網絡圖上增加關聯強度屬性，并以關聯影響最低為目標，提出了最優更改傳播路徑搜索算法；陳進平等[14]、劉彥臣等[15]以關聯網絡為基礎，分別采用深度及廣度優先算法，實現了關聯傳播范圍的求解和可行更改路徑的優選；TANG等[16-17]用設計結構矩陣描述產品的結構關聯，確定了工程變更傳播及影響范圍，提出了變更傳遞路徑的搜索算法；宮中偉等[18]以設計結構矩陣為基礎，提出了基于聯系依賴矩陣的工程變更雪崩傳播預測方法；CLARKSON等[19]提出了基于非布爾型設計結構矩陣的變更預測算法。

上述工作為基于關聯的尺寸更改傳播研究提供了可靠的理論基礎，但目前相關研究主要集中于產品結構更改的傳播以及參數變更對產品性能影響等方面。如何基于產品結構的層次與邏輯關系，研究尺寸特性的定量轉變方式和更改傳播的轉化特性，使得計算機技術能以更為有效的方式為設計自動化服務，是該領域面對的深層問題。

針對上述問題，本文進行了尺寸關聯更改傳播路徑生成方法的相關研究。為有效描述尺寸特性間的邏輯與層次關系，建立了由尺寸邏輯元、更改傳播邏輯元、尺寸更改傳播系數組成的關聯更改傳播模型，提出了基于零件關聯的尺寸更改傳播路徑識別與優選方法，給出了基于內積運算的尺寸關聯更改傳播路徑搜索算法，確定了更改尺寸在產品中的傳播過程與路徑。該方法從關聯角度描述了尺寸的關聯與傳遞關系，為工程更改傳播提供了尺寸特性更改傳遞的定量轉變方式。

1 尺寸關聯更改傳播模型的構成要素

更改傳播路徑借由零件間的多種關聯關系來表征。作為裝配結構的固有屬性，零件間的關聯關系具有多維性和復雜性等特點，零件自身的尺寸特性、相關零件的尺寸關聯特性以及尺寸關聯波動的強弱程度在尺寸傳播更改過程中具有關鍵的作用。為有效描述尺寸特性間的邏輯與層次關系，以尺寸邏輯元、更改傳播邏輯元、尺寸更改傳播系數作為尺寸關聯更改傳播模型的構成要素。

1.1 尺寸邏輯元

在尺寸更改設計迭代過程中，尺寸邏輯元是由零件(或組件，為簡化描述本文統稱為零件)的基本信息構成的基本單元，它也是尺寸關聯更改傳播的基本單元。通過尺寸邏輯元可以實現能量轉化、轉移，并完成尺寸更改的傳遞。圖1所示為尺寸邏輯元的一般化符號模型。

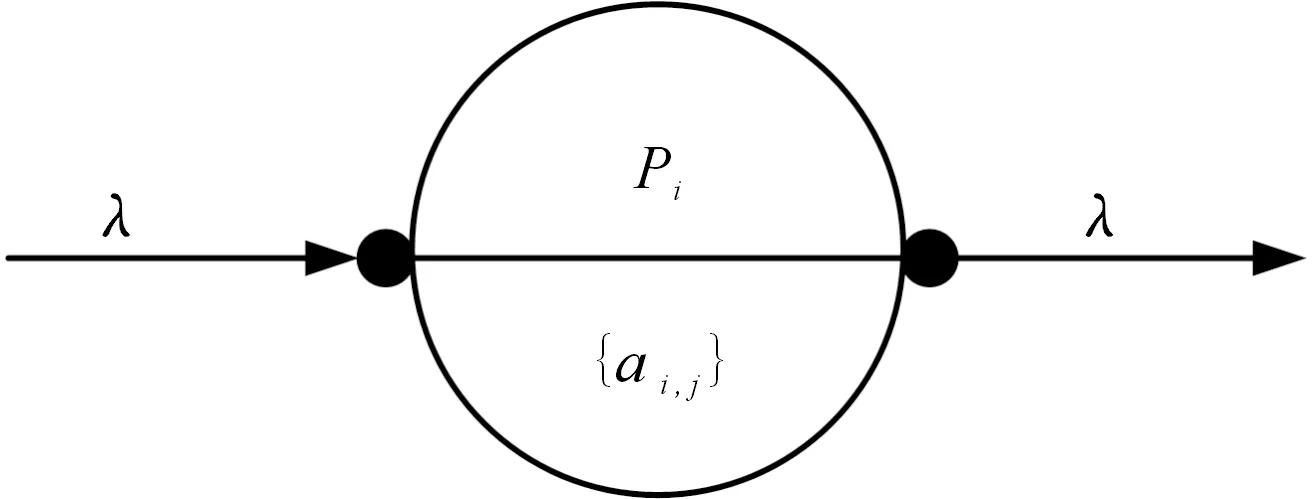
圖1 尺寸邏輯元模型Fig.1 Logical unit model of dimension

圖1中，Pi表示第i個零件；E(Pi)表示零件Pi的一組尺寸參數，主要是指工程更改發生時，零件Pi發生關聯變更的物理特性尺寸、幾何結構尺寸等；ai，j為零件Pi的第j個尺寸參數。定義

E(Pi)= {ai，1，ai，2，…，ai，n}

其中，n為零件Pi中發生關聯變更的尺寸參數數量(即集合E(Pi)中元素的數量)，并定義

EC(Ps，Pi)={ai，k1，ai，k2，…，ai，kt}

其中，EC(Ps，Pi)表示在更改傳播中當零件Pi更改時，對零件Ps尺寸參數產生影響的Pi的尺寸參數集合。ai，kt為會對零件Ps尺寸參數產生影響的零件Pi的第kt個尺寸參數，kt≤n，t為集合EC(Ps，Pi)中元素的數量，且有

EC(Ps，Pi)?E(Pi)

有向線段表示零件之間的尺寸關聯更改傳遞流，該線段的方向代表更改的流向及因果關系，線段的主要狀態參數包括尺寸變量的類型、大小和路徑，線段的特征值為尺寸更改傳播系數λ。

1.2 更改傳播邏輯元

相關聯零件之間的功能和結構連接關系(如尺寸特性之間的配合關系、輸入與輸出特性之間的匹配關系等)決定了設計更改從一個零件向另一個零件的傳播路徑與方式。為簡化更改分析，在梳理零件間復雜關聯關系的基礎上，基于尺寸更改傳播的特點，建立了構成更改傳播網絡的基本單元——更改傳播邏輯元，可分為如下三類。

(1)AND邏輯元。當某父代零件尺寸特性更改時，兩個或多個子代零件的尺寸特性必須同時更改，其模型結構如圖2a所示；當兩子代零件形成AND邏輯關系時，這兩個子代零件必然同時受其父代零件相同尺寸參數的影響，此時，EC(P2，P1) ∩EC(P3，P1)≠?。

(2)OR邏輯元。當某父代零件尺寸特性更改時，兩個或多個子代零件只需更改其中之一，如圖2b所示，此時，EC(P2，P1) ∩EC(P3，P1)=?；

(3)繼承邏輯元。當子代零件完全繼承父代零件的尺寸更改信息時，如圖2c所示，此時，EC(P2，P1)=E(P1)。

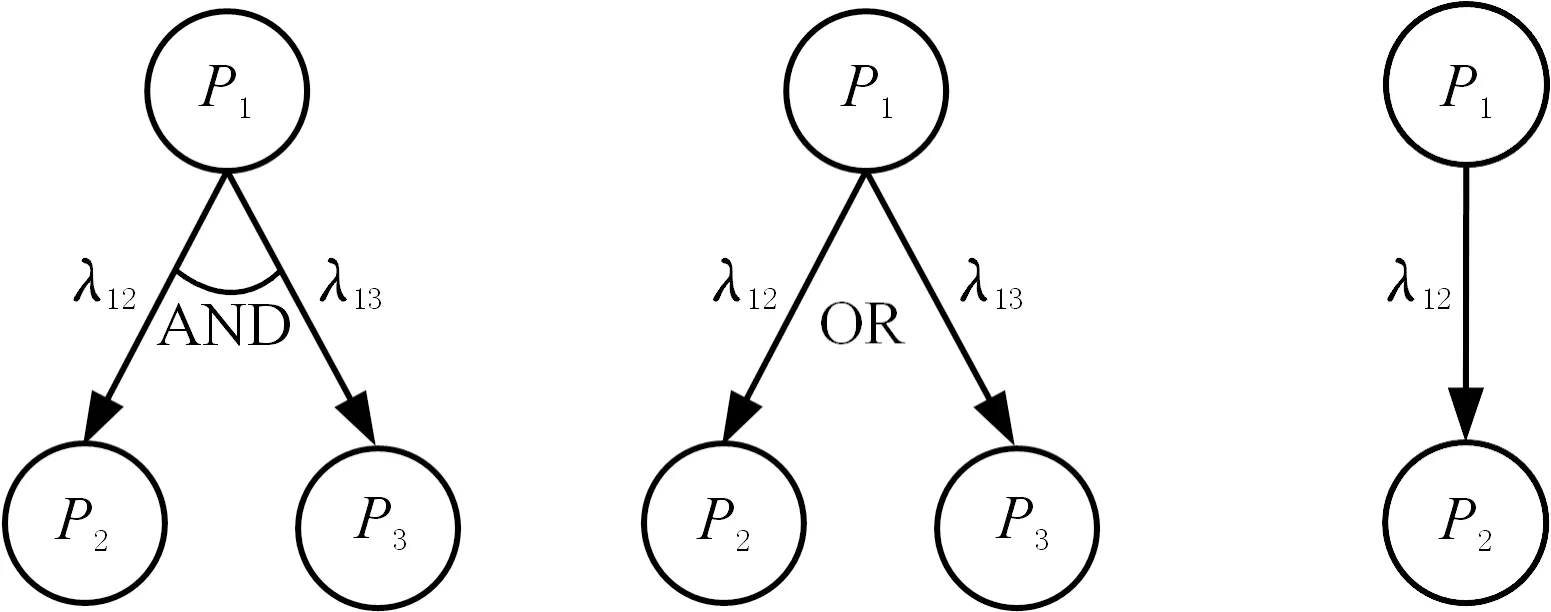
(a) AND邏輯元 (b) OR邏輯元 (c) 繼承邏輯元圖2 更改傳播邏輯元模型Fig.2 Logic unit model for change propagation

1.3 尺寸更改傳播系數

在尺寸關聯模型中，設計更改引發的波動是通過零件特性之間的連接對象進行傳播的，不同的連接關系對其特性的約束程度是不同的，其傳播更改的能力也存在差異。在此引入尺寸更改傳播系數來表征這種差異。

尺寸更改傳播系數λis用于表征父代零件Pi的尺寸更改對子代零件Ps尺寸的關聯影響程度。當僅考慮更改傳播邏輯元為AND和OR情況時，定義

(1)

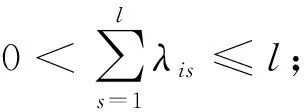
2 尺寸關聯更改傳播路徑規劃

識別可能的更改傳播路徑是進行更改傳播分析的一項重要前提。為簡化路徑搜索過程，本文采用從零件到尺寸的分層次路徑搜索方法。利用矩陣描述尺寸特性之間的關聯關系，基于邏輯運算識別它們之間的邏輯關系，并建立以零件為節點和以尺寸為節點的關聯更改傳播路徑，從而將工程更改影響分析中尺寸更改傳遞問題轉化為關聯矩陣運算問題。

由于在路徑搜索的不同階段涉及到不同的關聯矩陣，為方便運算，給出如下定義：

定義1 零件尺寸與零件間關聯矩陣：該矩陣基于尺寸特性之間的邏輯關系而形成，用以描述會對相關零件的尺寸參數產生影響的更改零件尺寸參數的情況。

定義2 尺寸關聯矩陣：用于描述相關零件尺寸特性之間關聯關系的矩陣。

零件尺寸與零件間關聯矩陣、尺寸關聯矩陣分別以零件、尺寸為目標對象，并分別用于建立以零件為節點和以尺寸為節點的更改傳播路徑。

2.1 以零件為節點的更改傳播路徑

2.1.1更改傳播路徑的初選

尺寸更改傳播發生的根本原因是產品內部零件尺寸之間存在相互關聯關系，因此，在更改傳播路徑初選的過程中，以零件為節點，依據零件之間的尺寸關聯關系建立更改傳播路徑并進行優選。具體步驟如下。

(1)建立產品關聯零件集合P={Pi}。

(2)建立尺寸邏輯元模型，并確定各零件的關聯更改尺寸參數集E(Pi)= {ai，1，ai，2，…，ai，n}。如有4個零件組成的裝配體，根據其尺寸關系可建立其尺寸邏輯元模型，如圖3所示。

圖3 尺寸邏輯元模型(示例)Fig.3 Dimension logic unit model(example)

(3)建立零件尺寸與零件間的關聯關系表征模型。主要包含如下幾個步驟：

第一步，建立零件間的關聯集值矩陣。根據所有參與關聯更改的零件間的尺寸關聯關系，以集合EC(Ps，Pi)為基礎，建立關聯集值矩陣R=[rsi]。該矩陣以零件為載體，通過建立會對相關零件尺寸參數產生影響的更改零件的尺寸參數集合來構建零件之間的關聯關系，其中

矩陣R中第s行第i列元素rsi表示對受影響零件Ps尺寸參數產生影響的更改零件Pi尺寸參數集合。為便于處理，規定矩陣中行零件與列零件的排序相同。以圖3為例，假設其關聯集值矩陣R如表1所示，表中元素為與行零件Ps的尺寸參數存在關聯關系的列零件Pi的尺寸參數集合。例如，由表1中第一行、第二列元素可知，列零件P2的尺寸參數a2，1、a2，2會對行零件P1的尺寸參數產生關聯影響。

表1 零件間的關聯集值矩陣

第二步，建立中間轉換矩陣。將矩陣R的列由零件擴展為該零件的尺寸參數，同時對矩陣R進行二進制轉化，用“1”、“0”分別表示列尺寸參數“是”或“否”會對行零件的某一尺寸參數產生影響，進而建立中間轉換矩陣，如表2所示。

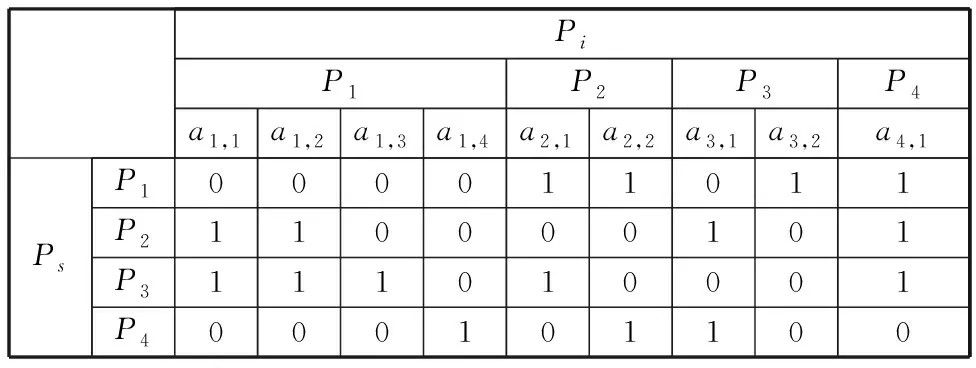
表2 中間轉換矩陣

第三步，建立零件尺寸與零件間的關聯矩陣。為便于運算，將中間轉換矩陣轉化為向量值矩陣C=[csi]l×l，其中csi為二進制向量，可表征對受影響零件Ps尺寸參數產生影響的更改零件Pi的尺寸參數情況，l為相關零件的數量。該矩陣更為直觀地描述了更改零件的尺寸參數對其余零件的影響。將表2所示的中間轉換矩陣轉換為向量值矩陣，可表示為

(4)根據是否被共同的父代零件尺寸參數所影響來確定子代零件之間的邏輯關系。若選取矩陣C中第i列零件Pi為更改零件(即更改源)，則對該列所有的非零向量兩兩進行“與”操作，根據“與”操作結果可以識別子代零件是否被共同的父代零件的尺寸參數所影響。本文采用“&”代表“與”操作運算符，對于零件Ps、Pm，若csi&cmi≠0(i≠m≠s)，則零件Ps與Pm之間的邏輯關系為AND，否則兩者之間形成OR關系；對于多個零件Pm、Ps、Pa、Pb，若(csi&cmi)&(cai&cbi)≠0(i≠m≠s≠a≠b)，則這些零件之間的邏輯關系為AND，否則為OR關系。上述圖3示例中，以列零件P1為父代節點，即以表1所示的矩陣R中第一列為更改源，以該列中的非零向量所對應的行零件為子代節點，依據上述方法可確定零件之間的AND、OR邏輯關系，進而可建立以零件為節點的第一層更改傳播路徑，如圖4所示。

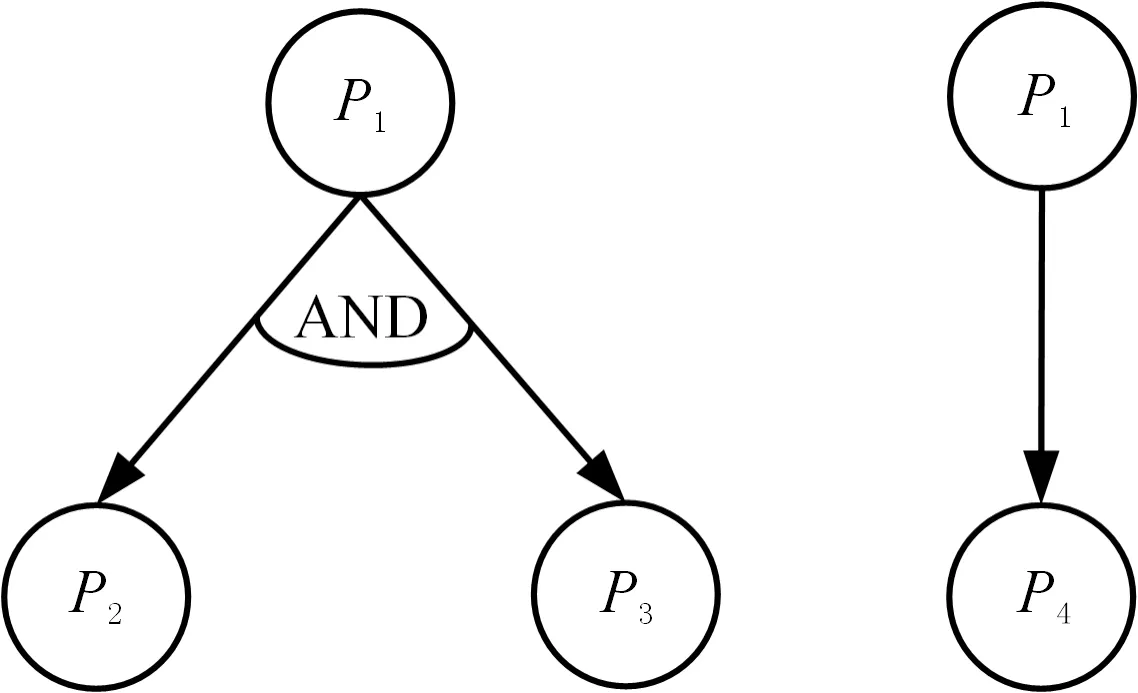
圖4 第一層更改傳播路徑(示例)Fig.4 First level change propagation path(example)

(5)以第一層更改傳播路徑的子代節點為更改源，重復步驟(4)，進行迭代搜索。

(6)搜索終止條件的確定。一般情況下，更改是單向的(即尺寸的更改不形成閉環反饋)，因此在搜索過程中，當路徑的某一分支中出現與父代節點相同的零件時，則搜索停止。在更改傳播路徑圖中，為表達搜索過程的完整性，將終止節點用虛線圓表示，且該節點不計入傳播路徑。基于上述過程，可得到圖3示例所示的以零件為節點的更改傳播路徑，如圖5所示。

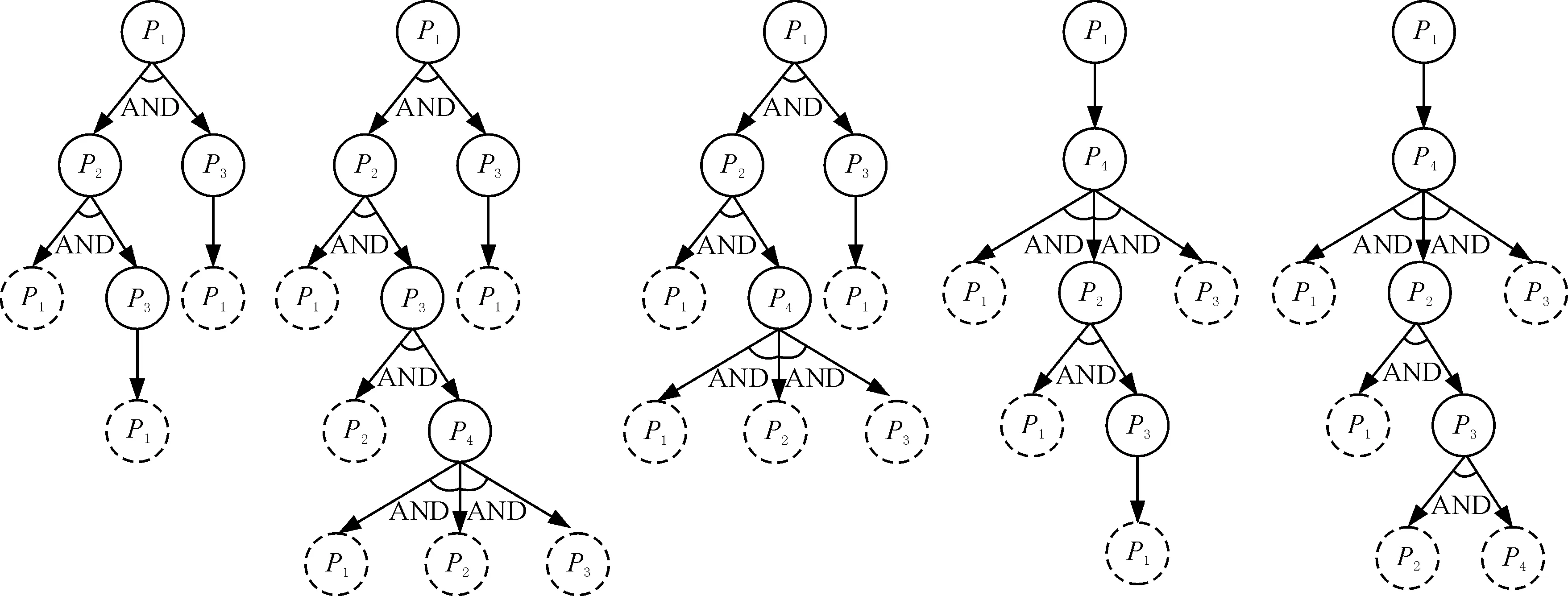
(a) 路徑1 (b) 路徑2 (c) 路徑3 (d) 路徑4 (e) 路徑5圖5 零件更改傳播路徑的初選(示例)Fig.5 Preliminary selection of part-based change propagation path(example)

2.1.2更改傳播路徑的優選

以零件為節點的更改傳播會形成多條路徑，如何從多條更改路徑中選擇一條經濟可行的方案是工程變更傳播需要解決的重要問題。路徑的優選涉及到幾何結構、配合關系、更改成本等多方面的內容，是個錯綜復雜的問題。本文僅從尺寸關聯及其變更成本的角度考慮路徑的優選問題。

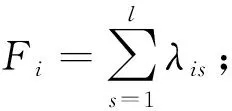
在不考慮其他約束條件的情況下，取評價指標值最小的路徑為最終更改傳播路徑。

2.2 以尺寸為節點的更改傳播路徑

基于2.1節所描述的過程，可得到以零件為節點的更改傳播路徑。但在更改傳播過程中，上層零件某一尺寸的更改并非直接反饋到下層相關零件的所有尺寸上，如何確定更改尺寸在零件確定尺寸間的傳遞過程與路徑，是最終進行尺寸傳播分析的基礎。

內積運算的物理意義是一個向量在另一個向量上的投影，其運算結果可以說明兩個向量在某一方向上的相互影響程度或接近程度。由此，本文以2.1節中所形成的零件間傳播路徑為基礎，基于內積運算，提出了以尺寸為節點的更改傳播路徑搜索算法。

根據以零件為節點的更改傳播路徑，首先建立關聯路徑圖上相鄰父子節點零件Pm、Ps之間的尺寸關聯矩陣為

D(Ps，Pm)=[duv]n1×n2

其中，n1為零件Ps的尺寸參數數量，n2為零件Pm的尺寸參數數量；在矩陣D(Ps，Pm)中，若零件Pm的第v個尺寸會對零件Ps的第u個尺寸產生影響，則duv=1，否則duv=0，在具體操作中，該矩陣可通過對建模軟件中特征尺寸之間關系的識別獲取。

為找出零件Pm的第v(1≤v≤n2)個尺寸所影響的零件Ps的尺寸參數集合，將ev與矩陣D(Ps，Pm)中的各行向量做內積運算，其中ev為內積運算算子，且ev為第v位為“1”的n2維單位向量；若ev與矩陣D(Ps，Pm)中第u(1≤u≤n1)行向量內積運算結果為1，則表明Pm的第v個尺寸參數會對Ps的第u個尺寸參數產生關聯影響。

以圖5b所示的路徑為例，采用上述內積運算方法即可建立以零件P1中尺寸參數a1，1為初始更改尺寸的尺寸傳播路徑，如圖6所示，具體步驟如下。

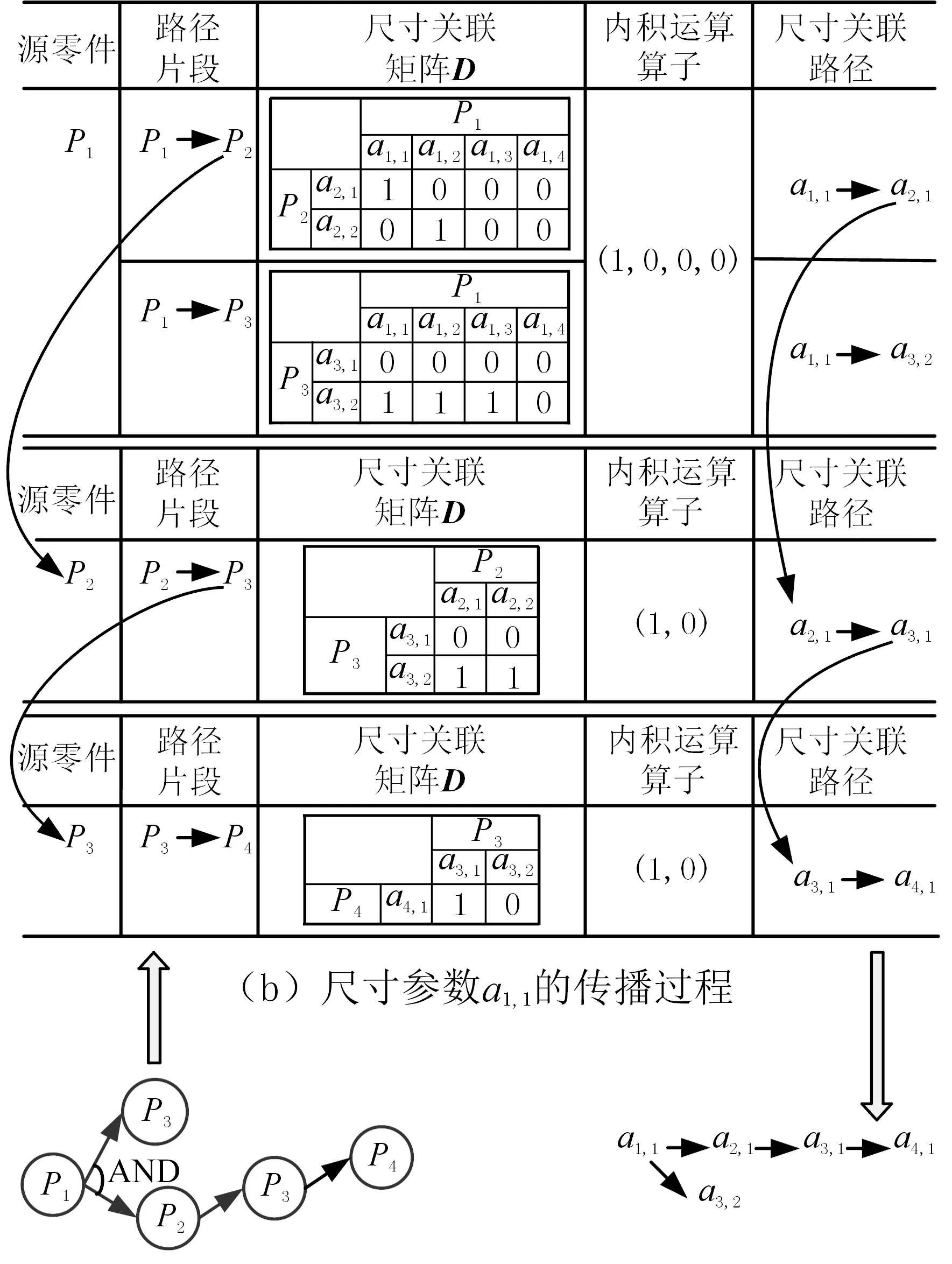
(a) 基于零件的更改 傳播路徑 (c) 尺寸a1，1的更改 傳播路徑圖6 尺寸參數a1，1的傳播路徑分析Fig.6 Analysis of the propagation path of a1，1

(1)刪除圖5b所示路徑的冗余節點，獲取簡化后的以零件為節點的傳播路徑，如圖6a所示。

(2)基于圖6a所示的以零件為節點的傳播路徑，分解出路徑片段；建立第一段路徑片段，即源零件P1與其子代零件P2、P3的尺寸關聯矩陣D(P2，P1)、D(P3，P1)。

(3)初始變更尺寸a1，1為零件P1中4個尺寸分量的第一個分量，其內積運算算子為e1=(1，0，0，0)；將向量e1與矩陣D(P2，P1)、D(P3，P1)的各個行向量分別做內積運算，得到尺寸a1，1所影響的零件P2、P3的尺寸分別為a2，1、a3，2，由此可得第一段尺寸傳遞路徑，即a1，1→a2，1，a1，1→a3，2。由圖6a可知P1→P3路徑終止。

(4)以零件P2為更改源，建立路徑片段P2→P3的尺寸關聯矩陣D(P3，P2)；依據尺寸a2，1在零件P2尺寸分量中的位置，將向量(1，0)與矩陣D(P3，P2)的各個行向量分別做內積運算，得到尺寸a2，1所影響的零件P3的尺寸為a3，1。

以此類推，可完成以尺寸a1，1為更改源的傳播路徑，如圖6c所示。

3 實例

本節以覆膜機為例說明上述方法的應用。圖7所示為覆膜機的結構模型。在工作過程中，送料機構對紙張進行運輸，然后由吸料部件將紙張吸起并傳遞到皮帶線1，由皮帶線1運送至覆膜卷處進行壓膜，壓好膜的紙張繼續傳遞到裁剪部位進行裁剪，最后經過皮帶線2完成覆膜。

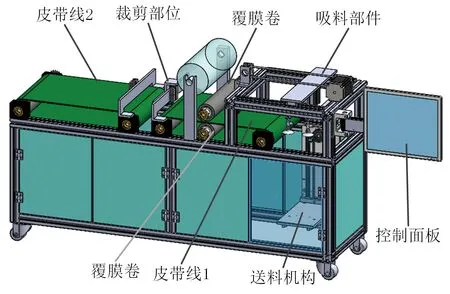
圖7 覆膜機結構模型Fig.7 Structural model of laminating machine

為簡化分析過程，本文只選取以圖8所示的機架結構、吸料部件與送料機構三個部件所構成的裝配體為例，分析尺寸更改傳播過程。

該裝配體中各零件的結構尺寸如圖8所示，圖中帶有箭頭的曲線表示零件之間存在裝配關聯關系。其中，機架P1與零件P3、P5、P7、P9、P10存在配合關系，氣缸安裝底板P2與零件P3、P4、P5存在配合關系，吸盤支架P8與零件P4、P6存在配合關系。各零件的關聯尺寸參數如下：

E(P1)={a1，1，a1，2，a1，3，a1，4，a1，5}

E(P2)={a2，1，a2，2}E(P3)={a3，1}

E(P4)={a4，1，a4，2，a4，3}E(P5)={a5，1，a5，2}

E(P7)={a7，1，a7，2}E(P8)={a8，1，a8，2}

E(P9)={a9，1，a9，2，a9，3}E(P10)={a10，1，a10，2}

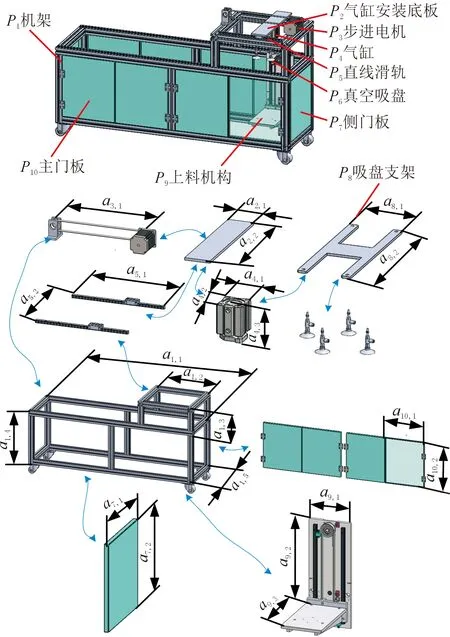
圖8 覆膜機尺寸及裝配關聯關系Fig.8 Dimension and assembly relationship of laminating machine

3.1 以零件為節點的更改傳播路徑

首先建立零件尺寸與零件間的關聯矩陣。根據零件間的尺寸關聯關系，建立基于尺寸關聯的覆膜機中間轉換矩陣，如表3所示。

表3 覆膜機中間轉換矩陣

然后確定子代零件之間的邏輯關系。為簡化描述過程，將其中一個零件作為更改源，并描述其更改傳播過程。在實際生產中，某一型號的覆膜機只能對特定尺寸范圍的紙張進行加工，當紙張尺寸變化超過該范圍時，則需要對覆膜機進行更改設計。由于紙張尺寸會對機架結構尺寸產生直接影響，因此將機架結構作為更改源。抽取表3中機架P1這一部分建立以機架為更改源的中間轉換矩陣，如表4所示。

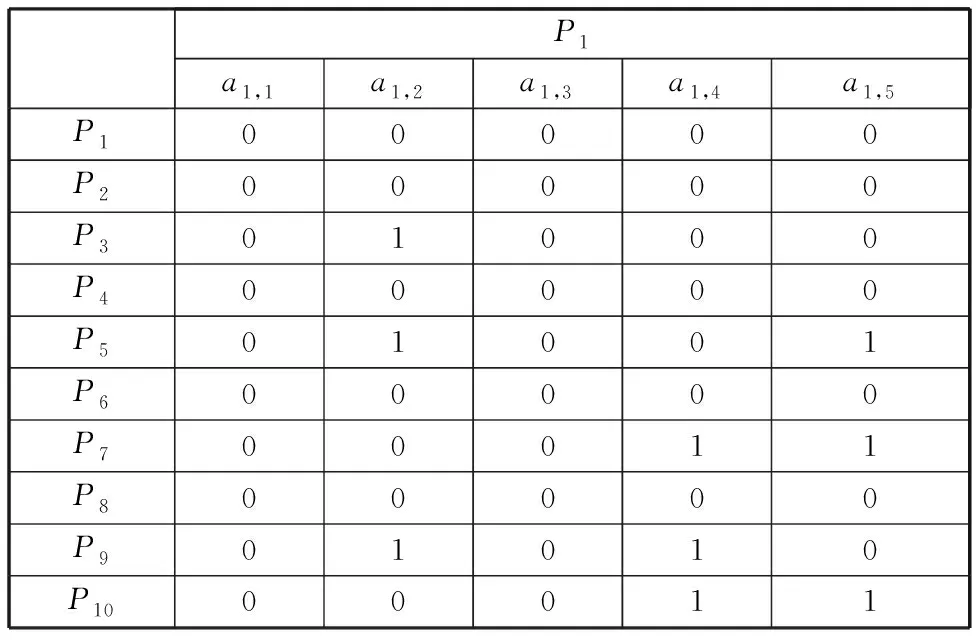
表4 機架作為更改源的中間轉換矩陣

在表4所示的矩陣中，零件P3、P5、P7、P9及P10所在的行向量非零，這些零件為受零件P1更改影響的零件，并對該矩陣的這些非零行向量兩兩進行“與”操作，有

P3&P5=(0，1，0，0，0)P7&P10=(0，0，0，1，1)

P7&P9=(0，0，0，1，0)P9&P10=(0，0，0，1，0)

均為非零向量。由此可得到零件間的更改傳播邏輯關系，見表5，其中，“A”、“O”分別代表零件之間的邏輯關系為“AND”、“OR”。

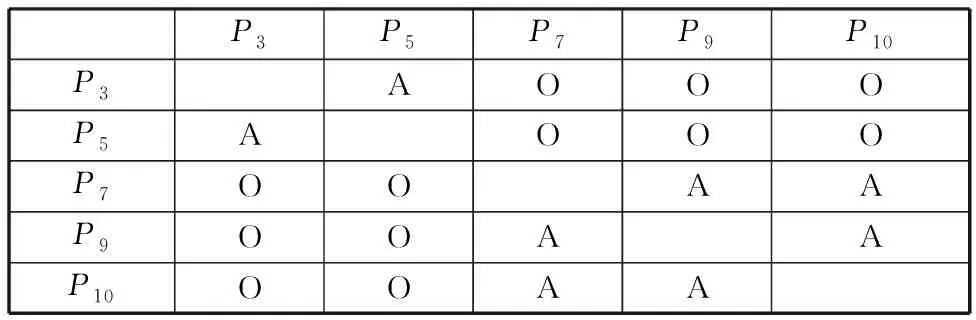
表5 零件間的更改傳播邏輯關系

依據表5可建立第一層更改傳播路徑，如圖9a所示。基于該路徑中的“OR”關系，第一層路徑可分解為兩個子路徑：①路徑1′為P1→(P3，P5)；②路徑2′為P1→(P7，P9，P10)。

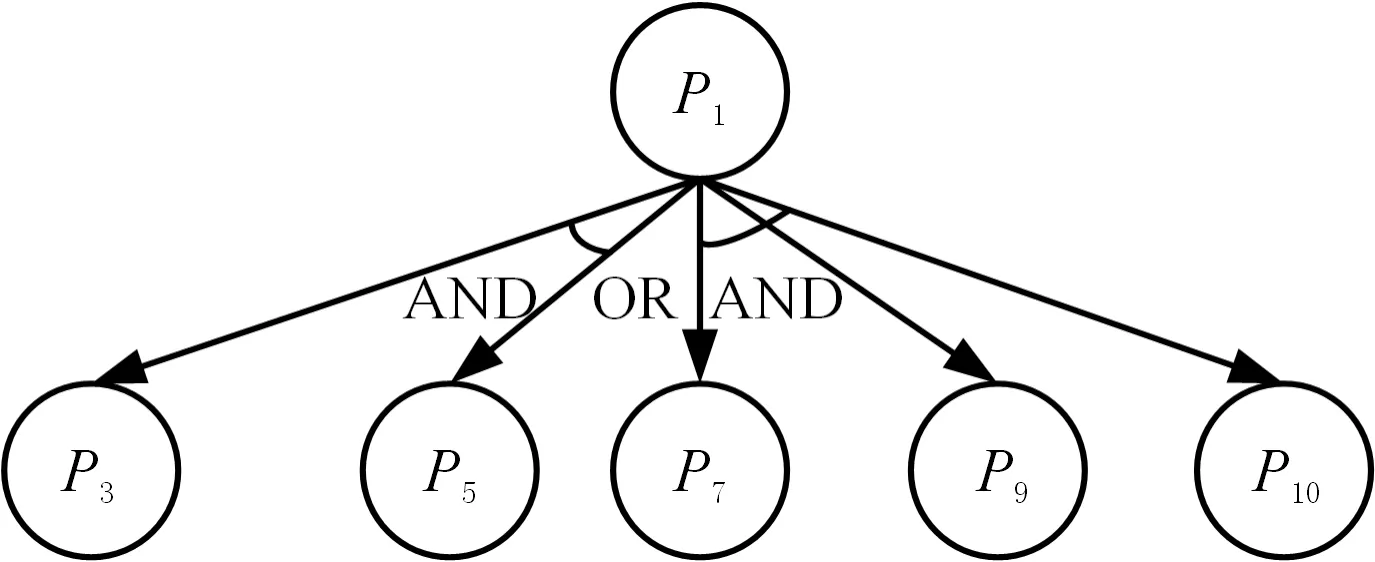
(a) 第一層路徑

將路徑1′中的P3、P5和路徑2′中的P7、P9、P10分別作為下一層更改源，重復上述運算，可得最終基于零件的更改傳播路徑：路徑1和路徑2，如圖9b所示。

3.2 以尺寸為節點的更改傳播路徑

建立關聯路徑圖上父代零件與其子代零件的尺寸關聯矩陣，分別如表6～表14所示。

表6 零件P1與零件P3尺寸關聯矩陣

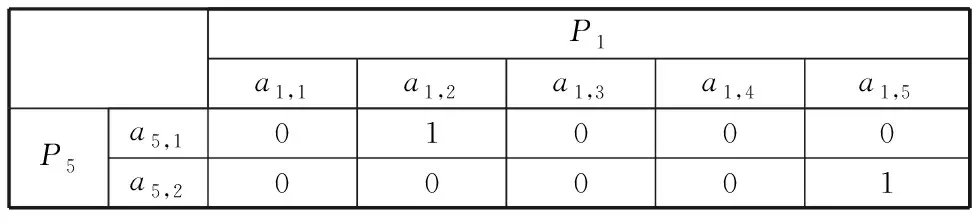
表7 零件P1與零件P5尺寸關聯矩陣

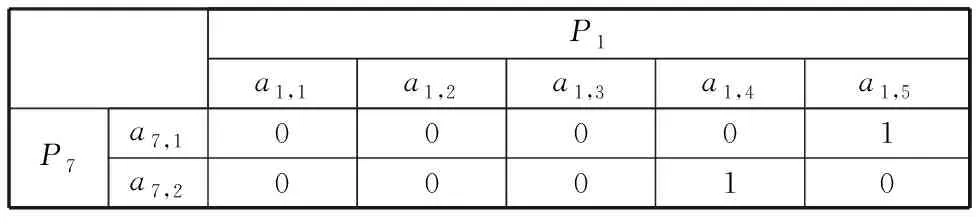
表8 零件P1與零件P7尺寸關聯矩陣

表9 零件P1與零件P9尺寸關聯矩陣

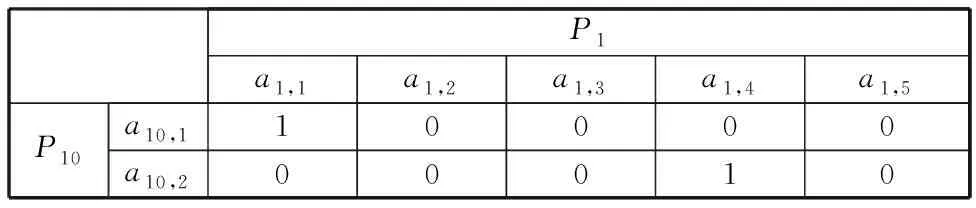
表10 零件P1與零件P10尺寸關聯矩陣

表11 零件P5與零件P2尺寸關聯矩陣

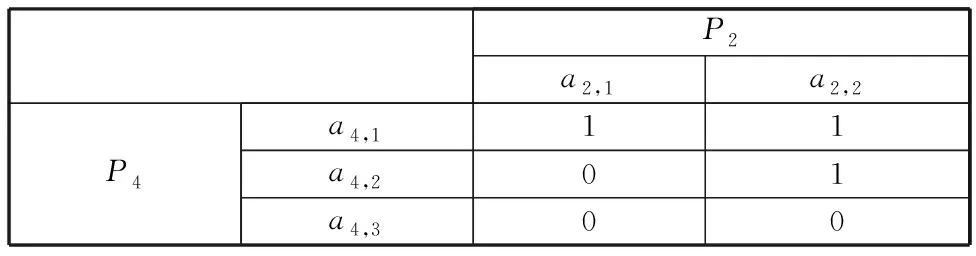
表12 零件P2與零件P4尺寸關聯矩陣

表13 零件P4與零件P8尺寸關聯矩陣

表14 零件P3與零件P2尺寸關聯矩陣

利用內積運算的方法，建立基于尺寸關聯的傳播路徑。如在路徑1中，父代零件為P1，子代零件分別為P3、P5，為求取尺寸a1，2的傳播路徑，可用向量(0，1，0，0，0)分別與表6和表7所示的矩陣中各個行向量做內積運算，可以得到零件P1中尺寸a1，2更改時的尺寸傳播路徑；同理也可得到零件P1中其他尺寸的傳播路徑。圖10所示為最終基于尺寸的更改傳播路徑。

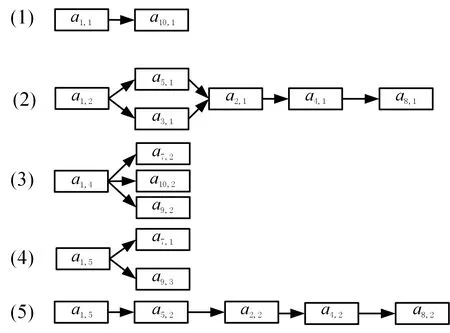
圖10 最終尺寸傳播路徑Fig.10 Final dimension propagation path

4 結論

(1)建立了以尺寸邏輯元、更改傳播邏輯元、尺寸更改傳播系數為基本構成的關聯更改傳播模型，實現了尺寸特性之間層次與邏輯關系的精準描述。

(2)分別采用矩陣運算及向量內積運算方法，建立了以零件為節點和以尺寸為節點的關聯更改傳播路徑，確定了更改尺寸在產品零件中相關尺寸間的傳遞過程與路徑。這種基于矩陣的分析方法，一方面實現了尺寸關聯關系由語義描述到數值描述的量化轉變，另一方面基于數學運算的更改傳播路徑搜索方法使得該方法更便于計算機表達與實現。此外，采用從零件到尺寸的分層次路徑搜索方法可顯著降低搜索的復雜性，從而提高了搜索效率。

本文所提出的方法可為深入研究尺寸更改傳播的內在機理提供一定的參考。但目前僅討論了單個零件發生尺寸變更后其更改傳播路徑的搜索方法，對于多零件以及多參數耦合更改方面的研究還有所欠缺，這也將是后續研究工作中擬進一步討論的問題。