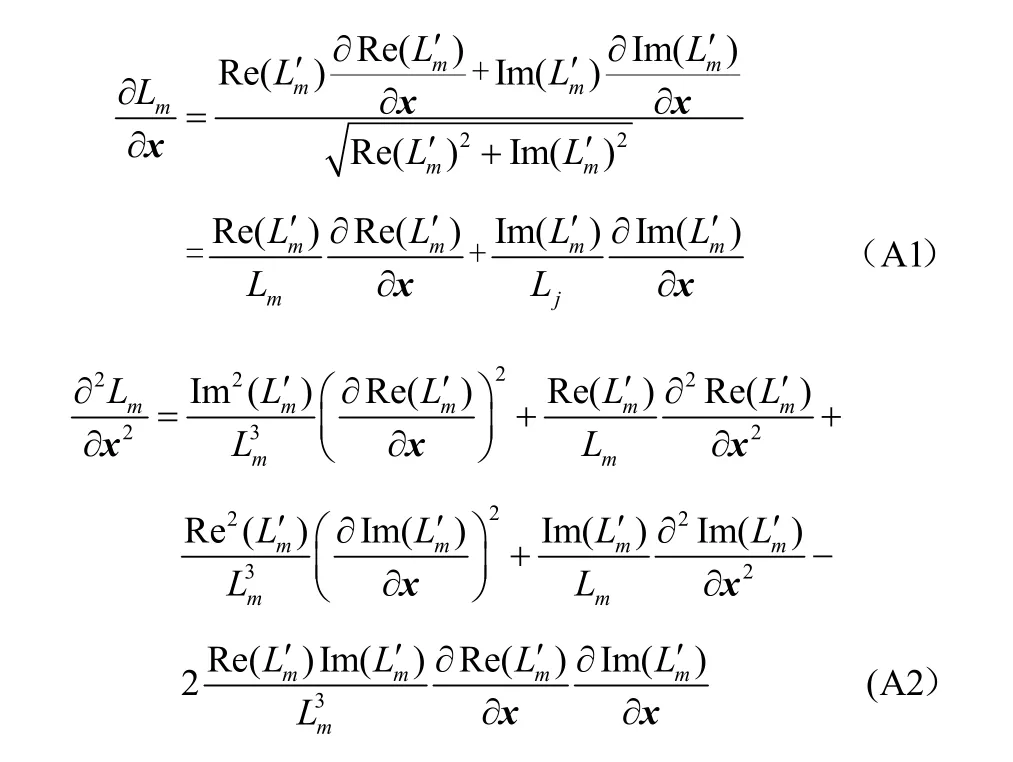基于擴展仿射模型的不確定性靜態電壓穩定性全局靈敏度分析

樂 健 廖小兵 李 奔 周子恒 彭學林

（1. 武漢大學電氣與自動化學院 武漢 430072 2. 國網鄂州供電公司 鄂州 436000 3. 國網武漢供電公司 武漢 430000）

0 引言

風電光伏發電等可再生能源集中式并網的規模日益增加，其出力的波動性將對接入系統的靜態電壓穩定性造成影響[1-2]。傳統靜態電壓穩定性分析以確定性潮流方程或擴展潮流方程為基礎[3]，忽略了可再生能源出力的波動性和負荷功率的時變性。確定性靜態電壓穩定性的評估結果已無法全面準確地反映系統電壓的運行態勢。

根據建模方式的不同，不確定性靜態電壓穩定性分析方法主要包括概率評估方法和區間評估方法。靜態電壓穩定性概率評估通常采用概率統計模型進行不確定量的建模，主要包括蒙特卡洛模擬法及改進方法[4-5]、點估計法[6]、半不變量法[7-8]、隨機響應面法[9]和最大熵估計法[10-11]等。靜態電壓穩定性概率評估需要建立不確定量精確的概率分布模型，而實際應用中輸入樣本數據往往不足，導致所建立的概率分布模型精度不高，因而，多數研究中需假設輸入不確定量服從某種概率分布，在一定程度上限制了靜態電壓穩定性概率評估方法的應用。

相比概率評估方法，靜態電壓穩定性區間評估方法僅需輸入不確定量的邊界信息，將不確定量波動范圍的上、下邊界描述為區間變量[12]，所需的統計信息較少，建模相對容易。文獻[13]將可再生能源出力的波動范圍上下界描述為區間輸入變量，采用仿射算術[14]將含區間變量的連續潮流模型轉換為仿射-線性優化模型求解。但基于極坐標系的連續潮流方程需要采用切比雪夫近似[15]對非線性三角函數估算，導致了區間擴張。文獻[16]采用基于直角坐標系的連續潮流方程，結合仿射-線性優化方法求解靜態電壓穩定裕度區間，但仿射乘法運算將不可避免地引入新的噪聲元，造成區間結果擴大。為此，文獻[17]通過優化改進仿射乘法運算來避免仿射乘法的區間擴張效應。文獻[18]通過建立風電場出力的概率區間分配模型，利用證據理論和雙層規劃方法求解靜態電壓失穩的概率區間。但上述靜態電壓穩定性區間評估方法仍存在如下兩個主要問題：

1）常用仿射算術以一階區間泰勒展開為基礎構建[19]，導致其在求解靜態電壓穩定裕度的過程中抑制區間擴張效應的能力有限，需要研究新的評估方法以降低評估結果的保守性。

2）常用仿射算術借助噪聲元的類同位素追蹤功能[20]來定性分析各輸入區間變量對系統輸出區間變量的影響，目前尚未可量化評估各輸入不確定量對靜態電壓穩定性影響重要程度的方法。

本文基于二階區間泰勒展開的擴展仿射算術[21]提出了不確定性靜態電壓穩定性的全局靈敏分析方法。首先根據擴展仿射算術構建基于L指標的靜態電壓穩定性評估模型。然后利用基于解析化方差分解的全局靈敏度分析方法定量評估各輸入區間變量對靜態電壓穩定性影響的重要性。通過IEEE標準測試系統中的多個仿真算例結果驗證了本文所提方法的正確性和有效性。

1 基于擴展仿射算術的靜態電壓穩定性評估模型

1.1 擴展仿射算術

式中，x0為標稱運行點或期望運行值；為由輸入擾動源變動所引入的噪聲元或仿射變量，各元素的取值范圍均為[-1 ,1]；系數x1為一階靈敏度系數向量，反映了仿射算子對噪聲元的線性變化大小。 常用仿射算術也稱為一階仿射算術，由于忽略了非線性項（二階項）對仿射算子的影響，很容易在區間計算過程中造成區間結果擴張[22]。因此，本文引入二階靈敏度系數，對常用的一階仿射形式（1）進行擴展，得到二階仿射形式，即

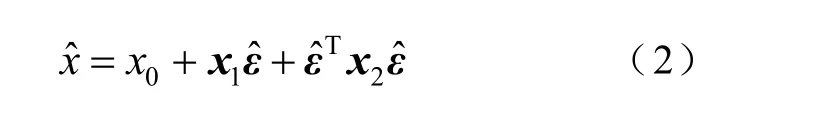
式中，系數x2為二階靈敏度系數矩陣，反映了仿射算子對噪聲元的非線性變化大小。

1.2 基于潮流解的靜態電壓穩定性L指標

評估靜態電壓穩定性的指標很多，主要包括靈敏度指標、奇異值指標、負荷裕度指標、L指標等。其中L指標物理概念清晰，計算速度快，被廣泛應用于在線靜態電壓穩定性評估[23]。本文選取基于潮流解的L指標來評估不確定性靜態電壓穩定性。

基于潮流解的L指標是表征實際狀態和穩定極限之間距離的量化指標，其值在0～1之間，用于描述電壓解的存在性。該方法的基本思路為：首先將所有節點劃分為發電機節點集合G（包括PV節點和平衡節點）、負荷節點集合D和網絡聯絡節點集合K，按三類節點建立網絡方程為

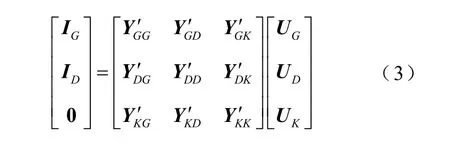
式中，UG和IG分別為發電機節點的電壓和電流向量；UD和ID為分別負荷節點的電壓和電流向量；UK為網絡聯絡節點的電壓向量；YG′G、YG′D、YG′K、YD′G、YD′D、YD′K、YK′G、YK′D、YK′K分別為相應節點的自導納或互導納子矩陣。

消去網絡聯絡節點K后，式（3）可簡化為

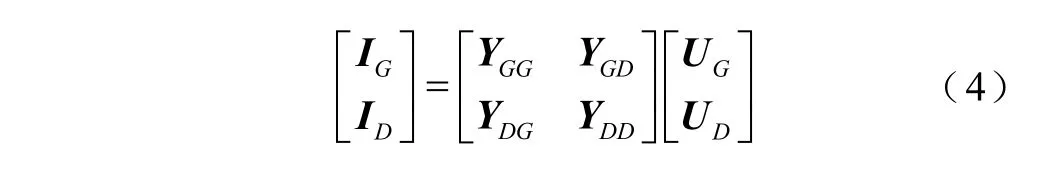
其中

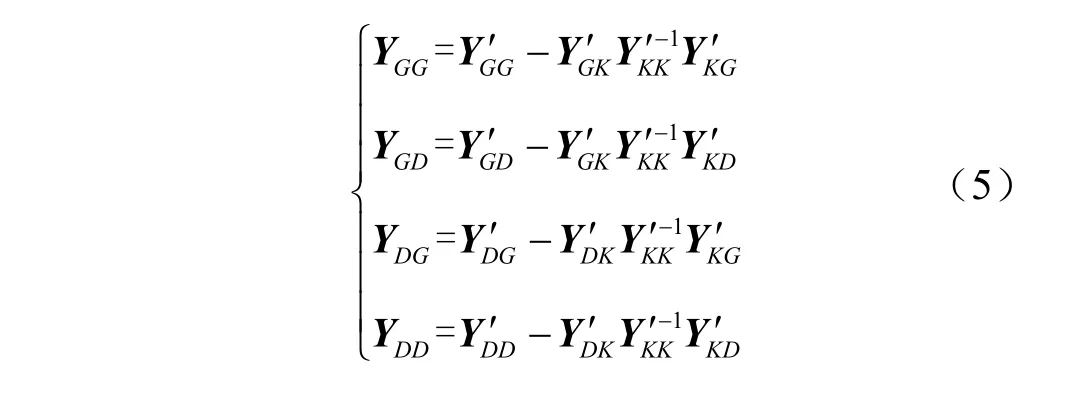
令ZDD=，式（4）可轉換為

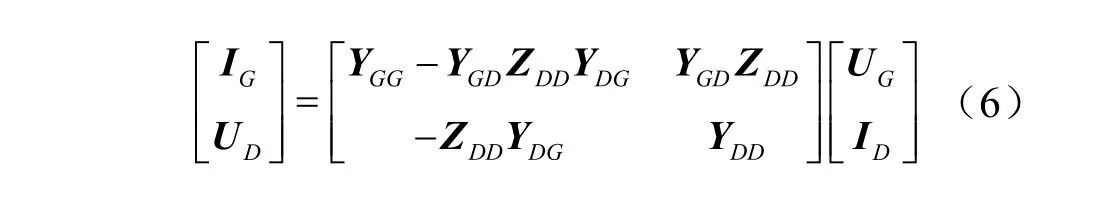
最后，求解負荷節點m(m∈D)，的靜態電壓穩定性指標為

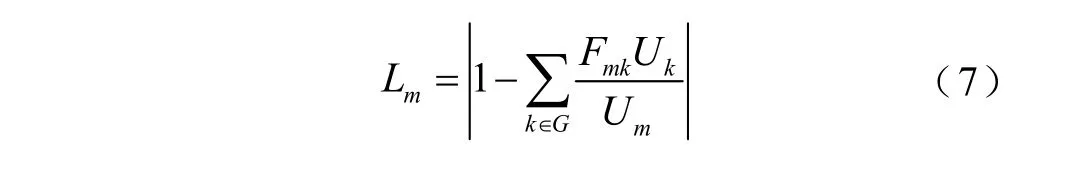
式中，Fmk為負荷節點參與因子，是矩陣F=-ZDDYDG的m行k列。

系統的靜態電壓穩定性指標L定義為

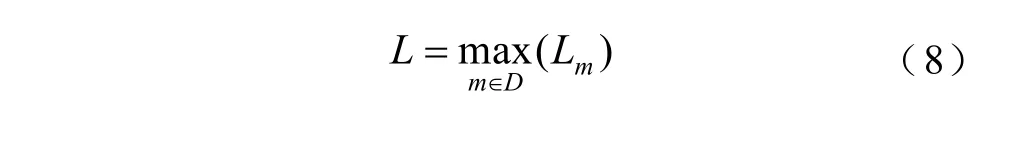
通過L值與1之間的臨近程度來表征全系統電壓發散程度[3]，當L＜1 .0表示系統電壓穩定，L=1.0表示系統電壓穩定臨界點，而L＞1 .0則表示系統電壓失穩。

1.3 基于L指標的靜態電壓穩定性區間評估模型

在1.2節靜態電壓穩定性L指標的基礎上，本節利用擴展仿射算術建立基于L指標的靜態電壓穩定性區間評估模型。

定義

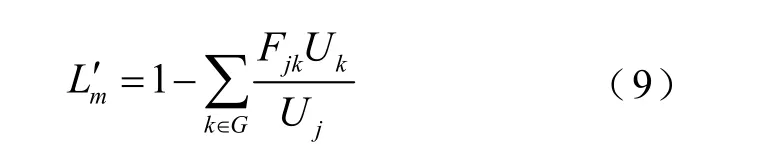
則式（7）可等效改寫為

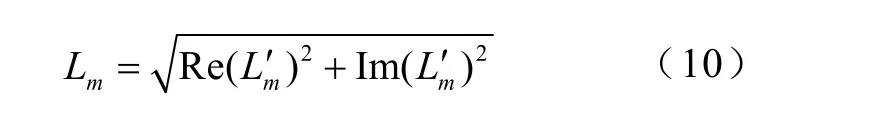
設直角坐標系下節點i電壓為Ui=ei+ jfi，負荷節點參與因子為Fjk=Gjk+jBjk，則的實部和虛部Im(Lm′)分別為

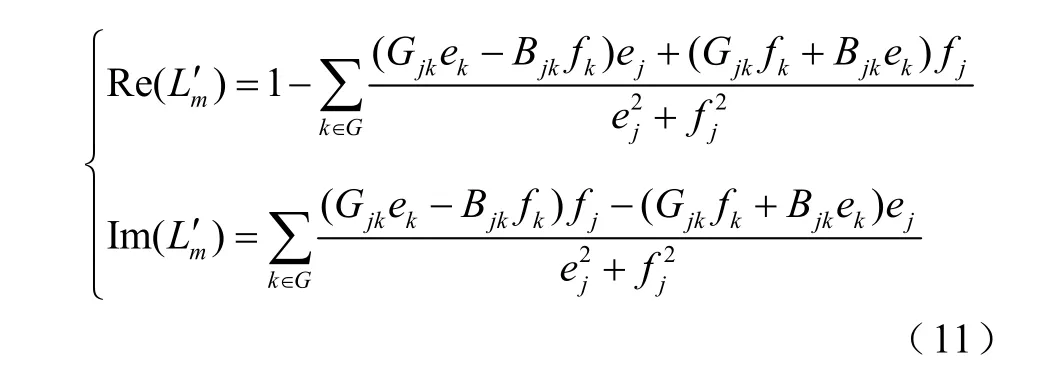
式（11）中的待求變量為ej、fj、ek、fk。

隨著節點注入有功功率和無功功率的隨機波動，各節點電壓也隨之變化，進而靜態電壓穩定性L指標也將跟隨變化。利用1.1節中的擴展仿射算術式（2）對節點注入功率擾動源進行二階區間泰勒展開，可得L指標的擴展仿射形式為

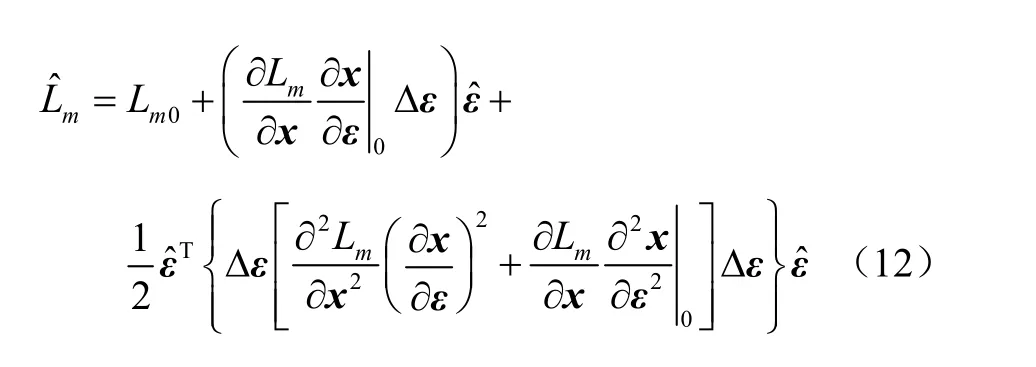
式中，Lm0為標稱運行點處的靜態電壓穩定性L指標值；分別為節點電壓待求變量x對輸入功率擾動源的一階、二階靈敏度系數矩陣，其詳細求解方法可參考文獻[23]；下標0表示在期望運行點處取值；Δε為注入功率擾動源的區間半徑；分別為L指標對節點電壓待求變量x的一階、二階靈敏度系數矩陣，其求解公式見附錄式（A1）和式（A2）。

因此，可構造以式（12）為目標函數（最大值即為上邊界，最小值即為下邊界）、噪聲元為約束條件的二次規劃模型，即靜態電壓穩定性L指標的擴展仿射優化模型?；跀U展仿射優化模型的靜態電壓穩定性評估方法通過二次規劃方法壓縮噪聲元范圍，得到L指標的區間結果，進一步可以判斷節點注入功率波動過程中系統是否失去靜態電壓穩定性。

從上述過程也可以看出：本文所提的擴展仿射方法是在確定性潮流基點的基礎上進行區間泰勒展開逼近，即標稱運行點處的解為基點，在輸入波動區間范圍內，先計算期望值處的L指標和相應的擴展仿射系數，利用區間泰勒展開就可以逼近L指標的區間范圍。因此，即使在輸入波動范圍內會出現病態潮流無解的現象，只要期望點處的確定性潮流有解，擴展仿射方法都能獲取L指標區間結果。

2 基于方差分解的靜態電壓穩定性全局靈敏度分析

通過靜態電壓穩定性擴展仿射評估模型可以真實地反映注入功率波動過程中L指標的區間范圍，但無法辨識出輸入擾動源對靜態電壓穩定性影響的重要性，只有對輸入擾動源進行重要性排序，才更有利于全面評估系統電壓的運行態勢。通常采用靈敏度分析來量化輸出響應中各輸入量的影響程度，但常用靈敏度分析方法是在某個固定點附近，每次僅對一個變量進行微小變化，而保持其他變量不變，即建立于局部線性化模型的基礎上，因此這類方法也被稱為局部靈敏度分析方法[24]。

局部靈敏度分析由于不能反映輸入變量波動對輸出響應的影響，已不適用于對不確定性系統的分析。全局靈敏度分析（Global Sensitivity Analysis, GSA）[25-26]從輸入變量的整個分布范圍來定量衡量輸入變量的不確定性對輸出量（例如模型輸出的方差或分布）的貢獻程度。方差是用來度量不確定量和期望運行點之間的偏離程度，可以反映不確定量的波動程度。通過將輸出響應的總方差分解得到各輸入量的方差貢獻，便能從輸入變量的整個波動區間范圍來量化輸入變量的波動對模型輸出響應的總方差貢獻程度。因此，基于方差分解的全局靈敏度分析方法（Variance Based Global Sensitivity Analysis）受到了越來越多的關注，其中Sobol'法[27]應用最為廣泛的。文獻[28]基于Sobol'法全局靈敏度分析理論，構建了考慮源荷不確定性的孤島微電網概率潮流全局靈敏度分析框架，并利用蒙特卡洛法求解了輸入不確定性量的一階全局靈敏度指標和總靈敏度指標。為了克服蒙特卡洛方法多次采樣耗時的缺陷，文獻[29]將概率潮流解用含隨機變量的稀疏混沌多項式表示，建立了基于稀疏多項式混沌展開（sparse Polynomial Chaos Expansion, sPCE）的孤島微電網潮流代理模型，只需少量的輸入和輸出樣本就可以確定稀疏多項式系數，從而實現了全局靈敏度指標的快速高效求取。但文獻[28-29]中均是基于獨立變量的方差分解方法，并未考慮輸入變量的相關性，文獻[30]進一步利用sPCE提出了計及相關性的區域電-氣聯合系統全局靈敏度分析方法。

但sPCE是基于隨機正交空間逼近理論，其逼近的精度決定了sPCE代理模型的準確性，它受輸入樣本空間大小和隨機采樣方法影響，因此，如何獲取最優輸入樣本成為提高其準確度的關鍵點。與上述思路不同，本文在靜態電壓穩定性擴展仿射模型的基礎上，提出考慮相關性的解析化方差分解方法，由于擴展仿射模型具有二階顯式表達，能快速、高效地將相關性方差和交叉貢獻進行分解。

2.1 靜態電壓穩定性L指標的總方差計算

基于擴展仿射模型的靜態電壓穩定性評估模型式（12）可以統一改寫為

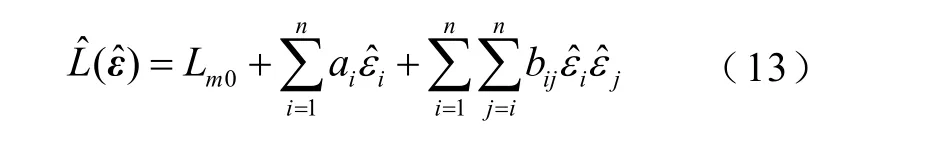
式中，n為輸入擾動源的維數；ai、bij分別為相應的一階、二階靈敏度系數。

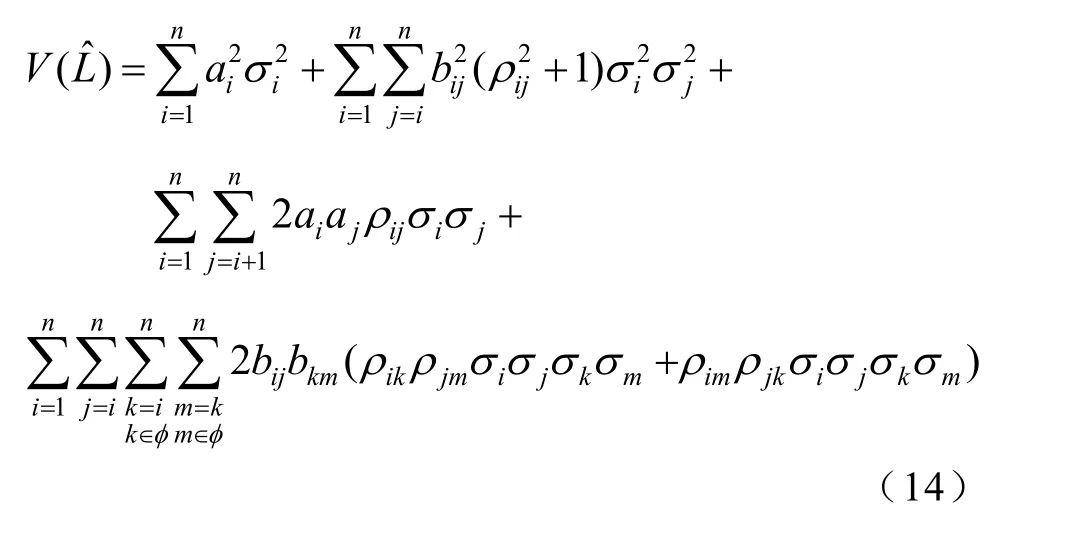
2.2 L指標的總方差的新分解形式

通過對輸出總方差式（14）的分解得到各輸入擾動源的方差貢獻量，就能清晰地辨識出各個擾動源對靜態電壓穩定性影響的重要程度。單個輸入擾動源的總方差貢獻分解框圖如圖1所示[32]。由于擾動源之間的相關性，單個輸入擾動源的總方差貢獻包括了總獨立性貢獻和總相關性貢獻，進一步總獨立性貢獻又可細分為獨立性主貢獻和各階獨立性交叉貢獻…，總相關性方差貢獻又可細分為各階相關性貢獻…。

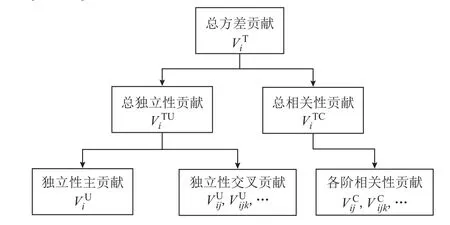
圖1 總方差貢獻新分解框圖Fig. 1 Novel decomposition framework of total variance contributions

2.3 基于新方差分解的全局靈敏度分析方法

基于方差分解的全局靈敏度分析是通過單個輸入變量的方差貢獻來反映各個輸入不確定量的影響程度，將單個輸入變量或者多個輸入變量的方差貢獻除以輸出響應的總方差，即為全局靈敏度指標。通過比較輸入擾動源的全局靈敏度指標大小便能清晰地辨識出對靜態電壓穩定性影響的主要因素和次要因素。本節在2.2節的基礎上定義兩類全局靈敏度指標：總靈敏度指標和主靈敏度指標。

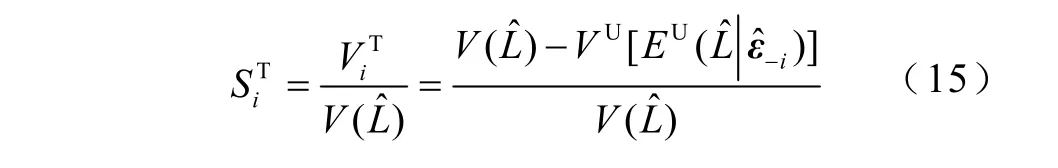
式中，VU、EU分別為不考慮之間相關性的方差、期望運算；為除之外的所有噪聲元?？傡`敏度指標又可分解為總獨立性靈敏度指標和總相關性靈敏度指標，即

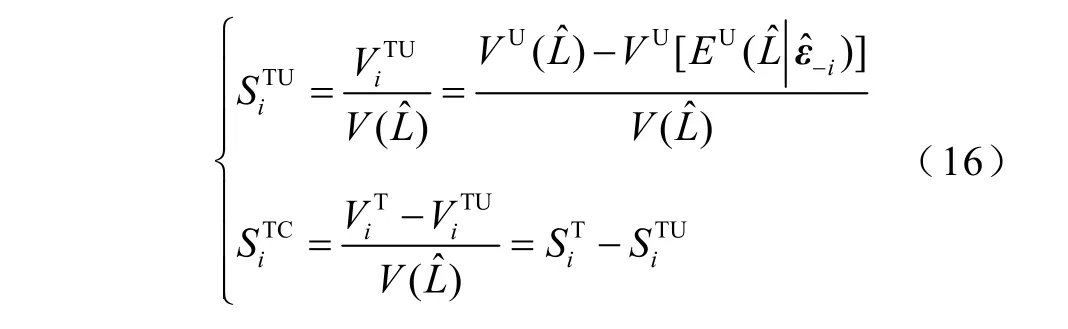
2）主靈敏度指標Si（或稱為一階獨立性靈敏度指標）

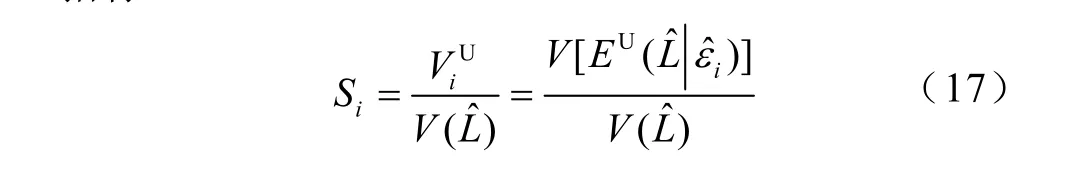
為便于理解，以一個簡單的含兩個相關性輸入變量的輸出響應函數為例，說明上述全局靈敏度指標求解方法。設輸入變量均服從正態分布，～N(0,Σ)，其中協方差矩陣Σ為

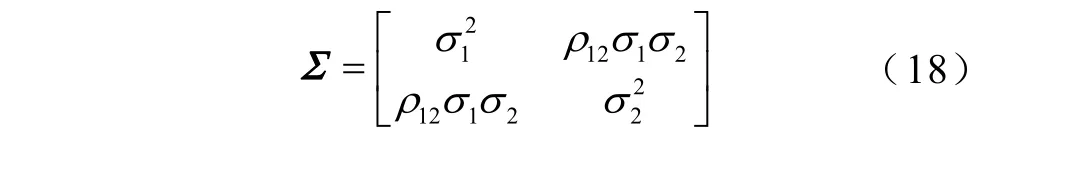
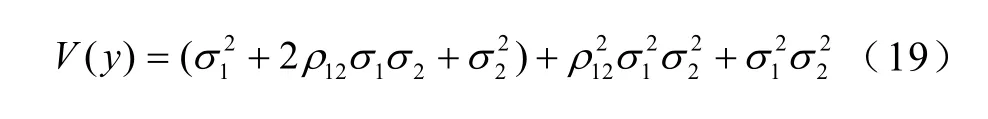
根據圖1得到輸出響應總方差貢獻分解結果見表1。

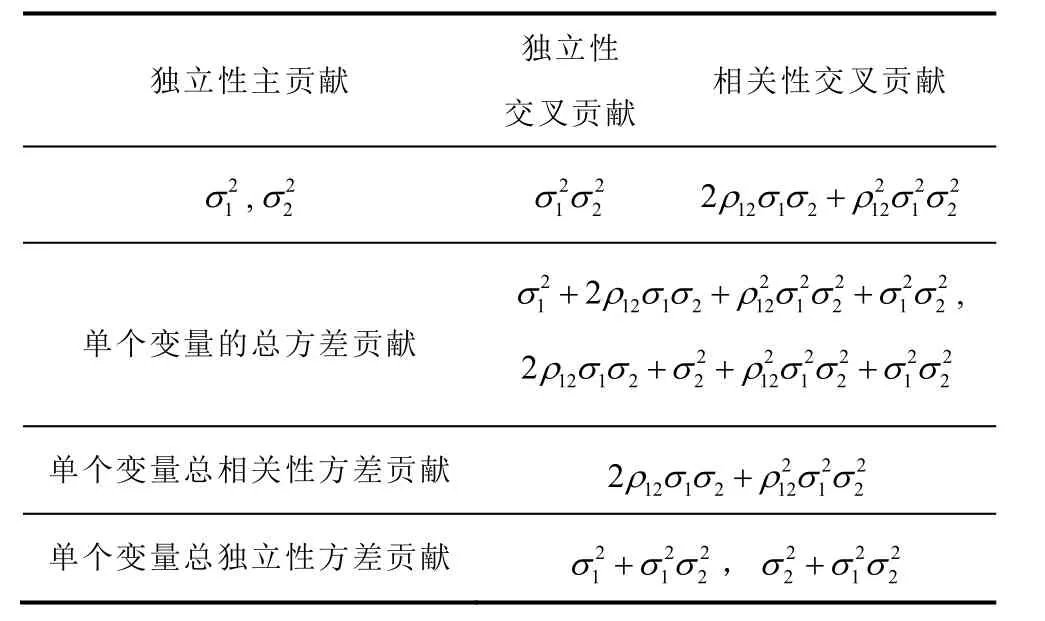
表1 輸出總方差貢獻分解結果Tab.1 Decomposition of total output variance contributions

由表1可知：通過輸入變量的總方差分解框架和計算公式，可以得出各個輸入變量的獨立性主貢獻、獨立性交互貢獻、相關性交互貢獻，也可以得到各個輸入變量的總相關性方差貢獻和總獨立性方差貢獻，這種分解形式有助于理清輸入變量總方差的組成成分，追蹤到關鍵環節。一旦獲取了這種解析化的方差分解形式，可以很容易獲得相應的全局靈敏度指標。當相關性系數ρ12= 0時，由相關性引起的相關性方差貢獻為零，即單個變量的總方差貢獻等于單個變量的總獨立性方差貢獻。因此，相關性系數為零時，本文所提出的全局靈敏度方差分解方法即退化為僅適用于獨立型變量的Sobol'法。因此，本文所提出的基于方差分解的全局靈敏度分析方法具有更廣泛的適用性。

3 算例測試與分析

3.1 有效性驗證

首先采用含風電場的IEEE 30節點系統作為算例對象，以驗證本文所提出的靜態電壓穩定性擴展評估模型的有效性。

含風電場的IEEE 30節點系統如圖2所示，三個風電場依次接入節點5、8、13。設風電場采用恒電壓控制方式，故可處理為PV節點。發電廠G1設置為平衡節點，設所有負荷節點和風電場節點注入功率為不確定性輸入變量，同時考慮風電場節點之間輸出有功功率之間的相關性。設不確定性輸入變量的均值為期望值或標稱運行點，標準差為相應均值的10%，三個風電場節點注入有功功率之間的相關性系數均為0.2。

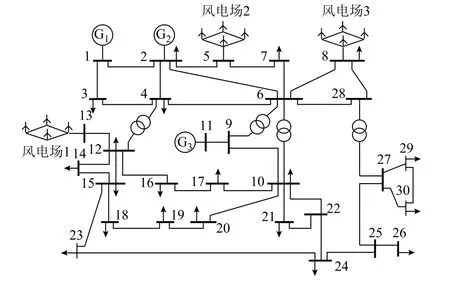
圖2 含風電場的IEEE 30節點系統Fig.2 Diagram of IEEE 30-bus system with wind farms

為驗證擴展仿射方法計算靜態電壓穩定性L指標的準確性，以蒙特卡洛方法多次抽樣仿真得到的區間結果作為靜態電壓穩定性L指標的對比標準。蒙特卡洛模擬作為一種隨機模擬技術，其模擬次數越多，計算結果越準確，但消耗計算時間也越多。測試中蒙特卡洛方法的抽樣隨機數在功率波動范圍內服從均勻分布，在抽樣次數超過1 800多次后，區間上、下邊界的誤差已經趨近于設置誤差精度10-3，故本文采樣2 000次作為其區間結果。分別采用擴展仿射方法（EAA）、仿射方法（AA）和蒙特卡洛方法（MC）三種方法求解各負荷節點L指標區間，并與確定性求解方法所得結果進行對比，結果如圖3所示。

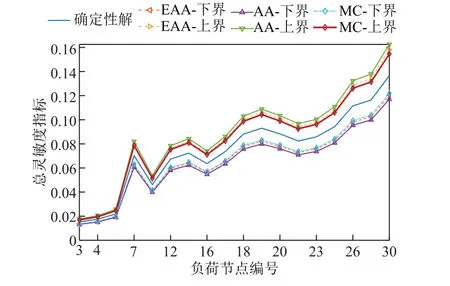
圖3 IEEE 30節點系統各負荷節點L指標區間結果Fig.3 Interval results of L index of each load node in IEEE 30 bus system

對比分析圖3中各方法所得L指標的區間結果，可得出如下結論：

1）三類區間評估方法所得L指標區間均包含了確定性方法所得的L指標。

2）采用擴展仿射方法和仿射方法獲得的L指標區間都嚴格包含了蒙特卡洛方法所得的區間，表明本文擴展仿射方法可嚴格獲取L指標區間解集的上、下邊界包絡線，驗證了本文所提出的靜態電壓穩定性擴展仿射評估模型的有效性。

3）以蒙特卡洛方法得到的結果作為“精確”的結果，可計算出擴展仿射方法和仿射方法計算得到的L指標平均估計誤差精度分別為1.58%和4.17%。

可見，盡管兩種方法均可得到準確的L指標區間結果，但基于擴展仿射方法的靜態電壓穩定性評估模型比基于仿射方法的評估模型獲取的L指標區間結果更為精確。這是因為基于擴展仿射方法的靜態電壓穩定性評估模型實質上是對L指標進行二階區間泰勒展開逼近，而仿射方法僅為一階區間泰勒展開逼近，二階項的計入使得擴展仿射方法獲得較常用仿射方法更高的計算準確度。

進一步，可從圖3中得出負荷節點30處的L指標最大，因此本節以負荷節點30處的L指標為例，對比分析輸入變量不確定時負荷節點30處L指標的總靈敏度指標和主靈敏度指標。表2和表3分別 給出了不考慮相關性和考慮相關性且相關性系數為0.2時，部分輸入不確定量對負荷節點30處的L指標的總靈敏度和主靈敏度。

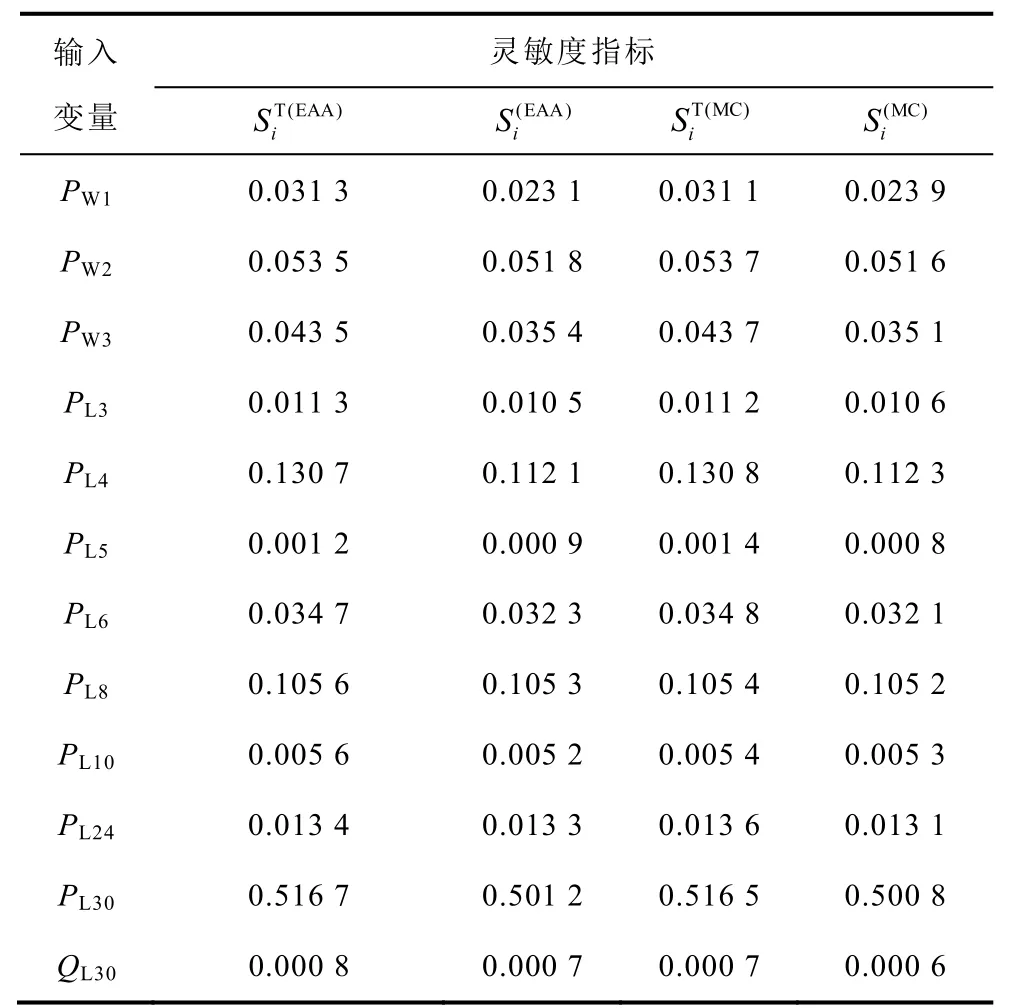
表2 部分輸入變量的總靈敏度指標和主靈敏度指標 (不考慮相關性)Tab.2 Total sensitivity index and main sensitivity index of some input variables (without considering the correlation)

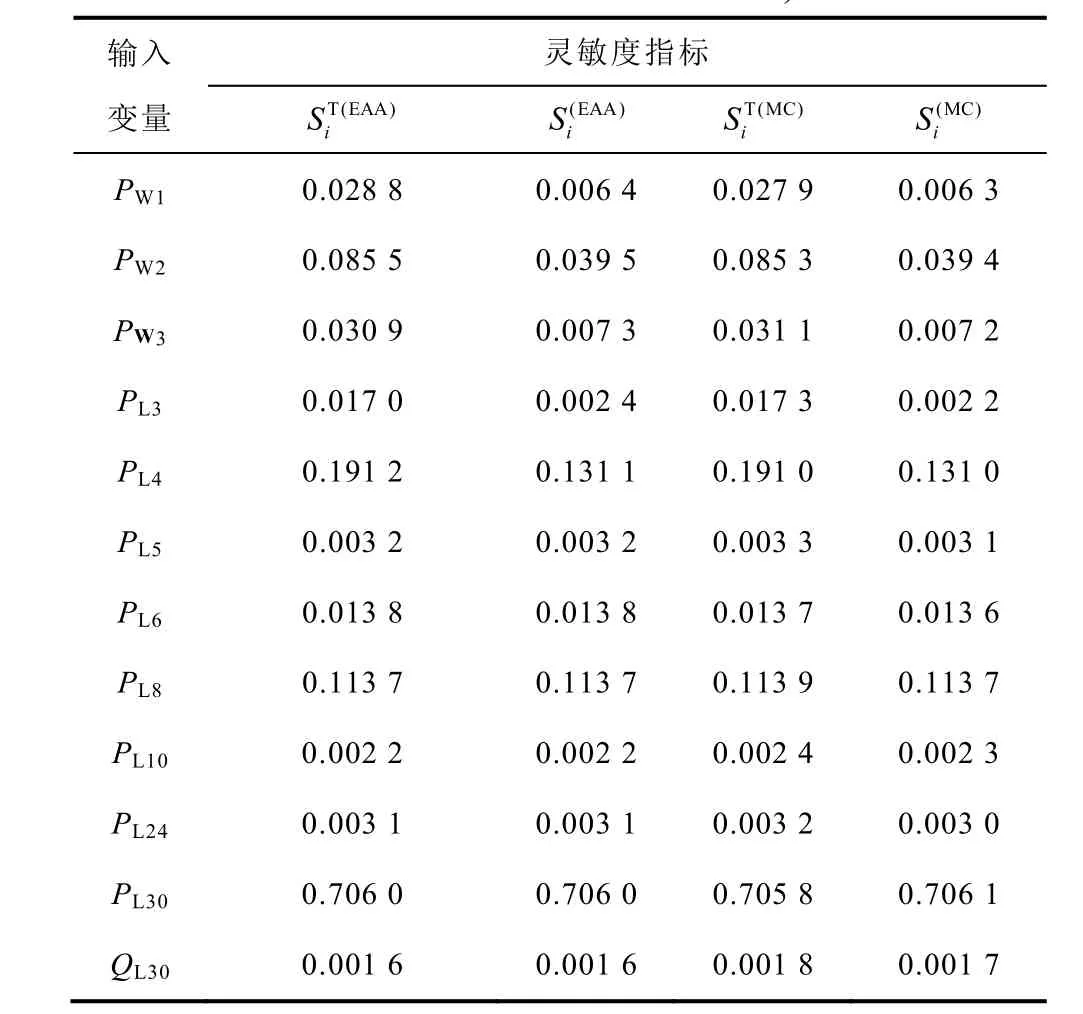
表3 部分輸入變量的總靈敏度指標和主靈敏度指標 (考慮相關性且相關系數為0.2)Tab.3 Total sensitivity index and main sensitivity index of some input variables(considering the correlation and The correlation coefficient is 0.2)

在不考慮相關性時，與蒙特卡洛方法（即為經典的Sobol’法）所得結果進行對比分析可以發現，基于擴展仿射方法獲得的總靈敏度指標與蒙特卡洛方法的最大相對誤差小于14.29%，主靈敏度指標的最大相對誤差小于6.8%。在考慮相關性時，與蒙特卡洛方法所得結果進行對比分析可以發現，基于擴展仿射方法獲得的總靈敏度指標與蒙特卡洛方法的最大相對誤差小于11.1%，主靈敏度指標的最大相對誤差小于9.1%，從而驗證了基于擴展仿射模型的全局靈敏度分析方法的有效性。

在不考慮相關性時，將表2全局靈敏度指標值由大到小排序，即為PL30＞PL8＞PL4＞PW2＞PW3＞PW1；而在在考慮相關性時，將表3全局靈敏度指標值由大到小排序，即為PL30＞PL4＞PL8＞PW2＞PW3＞PW1，可以看出考慮風電場輸出功率的相關性對全局靈敏度度指標的影響。因此，在全局靈敏度分析各輸入不確定量對L指標影響的重要性時需要計及相關性的影響。

表3表明1、2、3號風電場總靈敏度指標分別為0.028 8、0.085 5、0.030 9，即輸出有功功率的不確定性對負荷節點30處的L指標影響最大是2號風電場，3號風電場居中，而1號風電場最小。此外，30號負荷節點的有功功率需求的不確定性對該節點的L指標貢獻最大，達到0.706 0。

圖4和圖5進一步給出了所有負荷節點L指標的總靈敏度指標和主靈敏度指標。對比兩圖可知：主靈敏度指標和總靈敏度指標之間存在一定差異，這是因為主靈敏度指標僅考慮輸入變量的一階方差貢獻，而總靈敏度指標反映了相應輸入變量的總方差貢獻，即包括了輸入變量之間相互作用產生的一階及高階靈敏度。因此，主靈敏度指標和總靈敏度指標之間的差異性表明了輸入變量之間相互作用的方差貢獻。

圖4 所有負荷節點L指標的總靈敏度指標Fig. 4 Total sensitivity index of L index of all load nodes

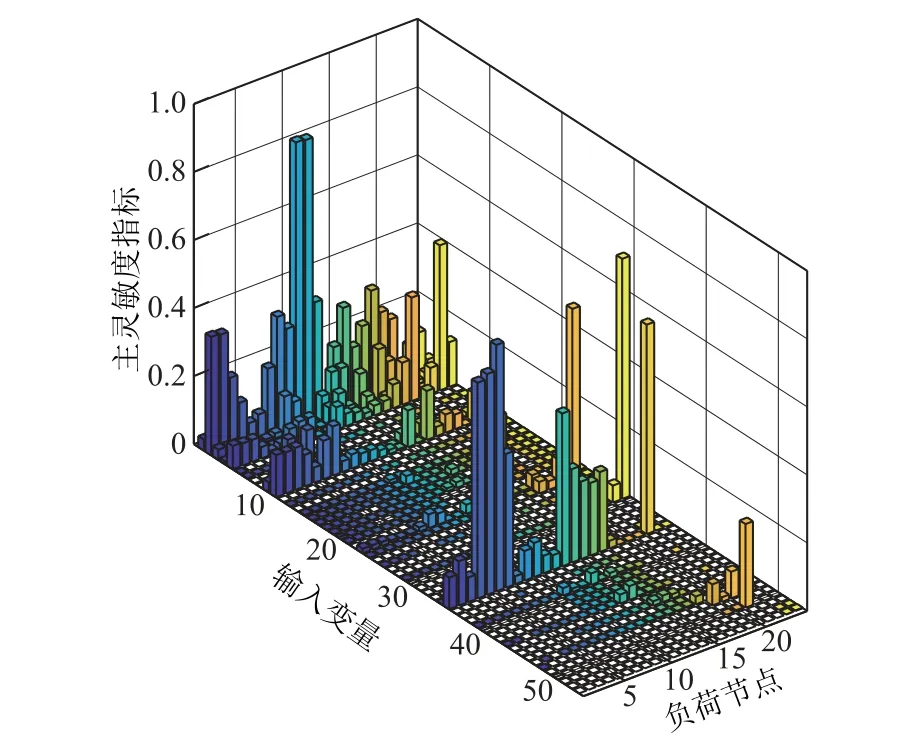
圖5 所有負荷節點L指標的主靈敏度指標Fig. 5 Main sensitivity index of L index of all load nodes

為驗證擴展仿射方法應用于靜態電壓穩定性全局靈敏度分析的魯棒性優于常用的仿射方法，本文將輸入變量的標準差分別設為相應均值的10%、20%、40%、80%，計算得出輸入變量PW1、PW2、PW3對負荷節點30處的L指標的總靈敏度指標和主靈敏度指標見表4。

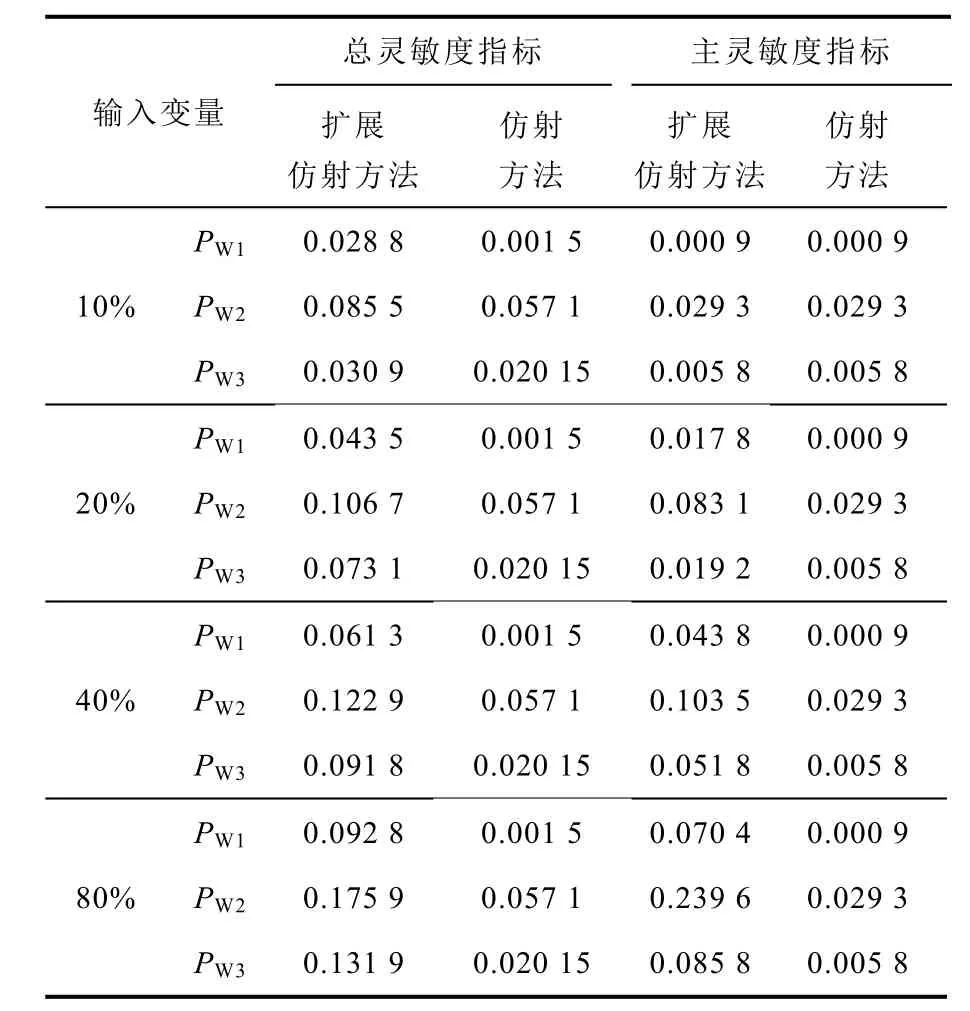
表4 負荷節點30 L指標的總靈敏度指標和主靈敏度指標Tab.4 Total sensitivity index and main sensitivity index of L index of 30 load node

從表4中可以看出，由于傳統仿射方法忽略了二階項的影響，使得基于仿射模型的全局靈敏度分析方法得到的三個風電場輸出功率變量的總靈敏度指標和主靈敏度指標隨標準差的增大而保持不變，即總方差貢獻與輸入變量的標準差無關；而擴展仿射方法能清楚地揭示三個風電場輸出功率變量PW1、PW2、PW3的總靈敏度指標和主靈敏度指標隨輸入變量標準差的增大而增大的變化趨勢，這與式（14）給出的結果一致。因此，采用擴展仿射方法得到的總靈敏度指標和主靈敏度指標能更準確地揭示輸入變量波動對L指標影響的變化規律。

3.2 相關性分析

以IEEE 30節點系統為例，設風電場的輸出有功功率PW1、PW2、PW3之間存在相關性，圖6給出了相關系數從-1到1變化時系統L指標的總靈敏度 指標的變化趨勢。

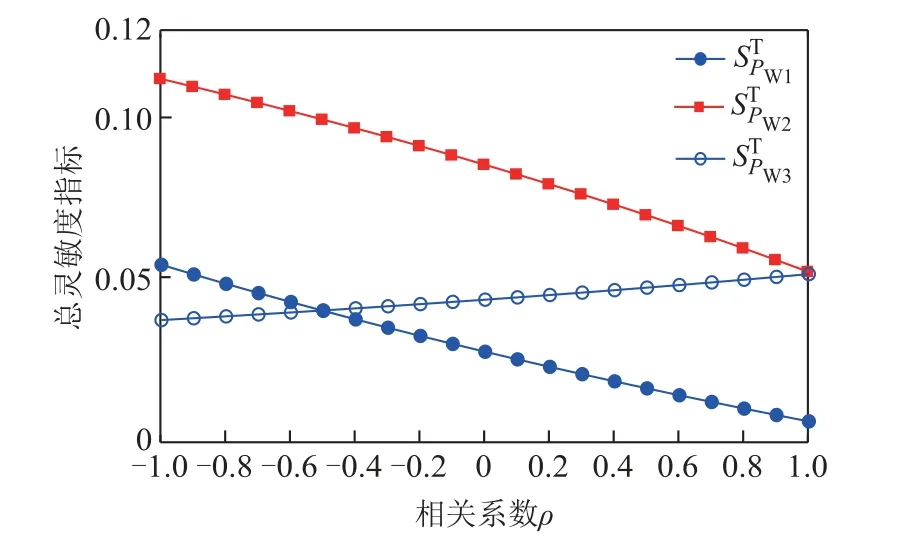
圖6 系統L指標的總靈敏度指標隨相關系數的變化曲線Fig.6 Change curve of total sensitivity index of system L index with correlation coefficient

圖6表明，風電場輸出有功功率PW1和PW2的總靈敏度指標隨著相關性系數的增加而下降，而風電場輸出有功功率PW3的總靈敏度指標隨著相關性系數的增加而緩慢增加。通過比較風電場輸出有功功率PW1、PW2和PW3的總靈敏度指標變化曲線的斜率不難看出：相關性系數對風電場輸出有功功率PW1和PW2的總靈敏度指標的影響明顯大于風電場輸出有功功率PW3。

3.3 計算效率比較

本文所提出的基于擴展仿射模型的靜態電壓穩定性全局靈敏度分析是一種解析式的方差分解方法，計算量小且計算效率高。在IEEE 30、IEEE 300和Case-2383算例系統中分別應用本文擴展仿射方法與蒙特卡洛方法，不同波動場景下兩種方法的計算時間和平均誤差統計于表5。其中的“平均誤差”表示所有負荷節點的靜態電壓穩定性L指標的全局靈敏度指標相對誤差的平均值；在IEEE 300和Case-2383中蒙特卡洛法分別模擬5 000次和10 000次。

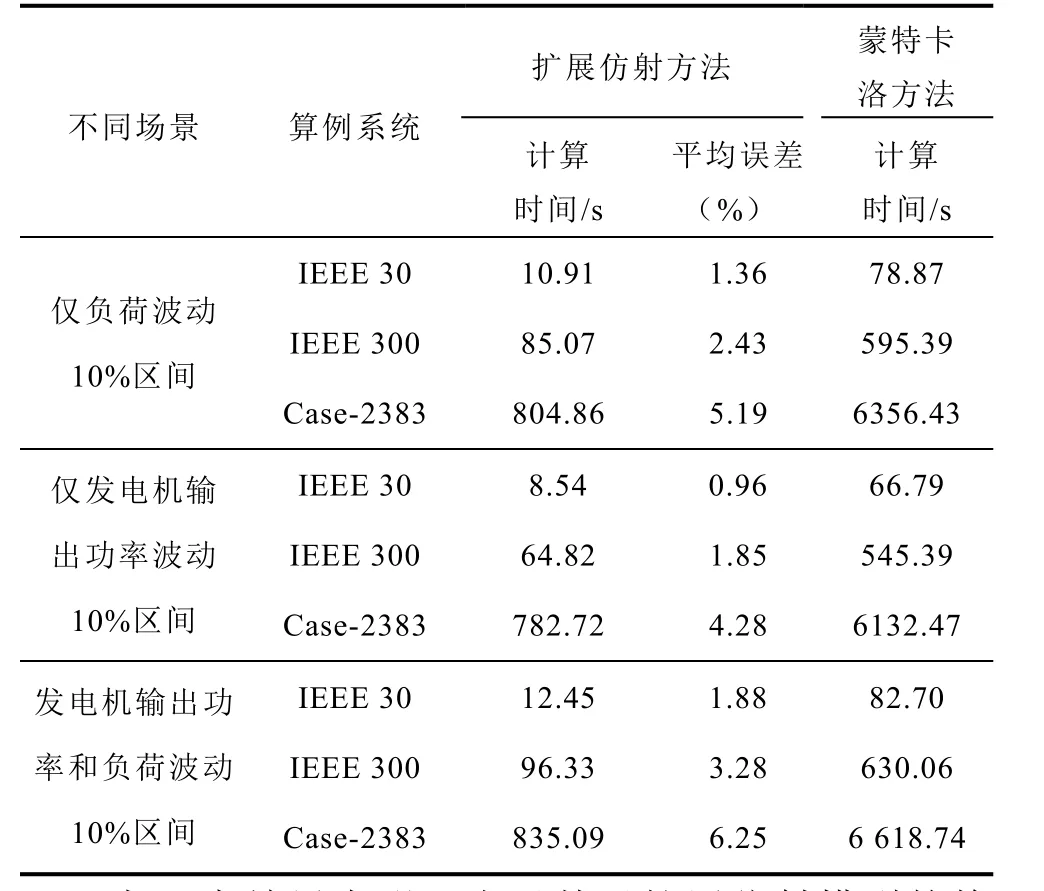
表5 不同波動場景下計算時間和計算精度比較Tab.5 Comparison of calculation time and accuracy in different fluctuation scenarios

表5中結果表明，由于基于擴展仿射模型的靜態電壓穩定性全局靈敏度分析方法具有解析化計算模式，相對于多次模擬采樣的蒙特卡洛方法，其計算時間明顯縮短，加速比可達到6～9。此外，與蒙特卡洛方法相比，基于擴展仿射模型的靜態電壓穩定性全局靈敏度分析方法具有很高的準確度，平均誤差最大不超過6.25%；系統規模擴大時靜態電壓穩定性靈敏度指標的平均誤差將有所增加。

4 結論

本文考慮新能源場站自身輸出功率的波動性和場站間輸出功率的相關性，利用擴展仿射方法構建系統靜態電壓穩定性評估的擴展仿射模型，可得到系統靜態電壓穩定性L指標的區間邊界，同時能辨識出系統中的薄弱節點。進一步將基于解析化方差分解的全局靈敏度分析方法和靜態電壓穩定性評估的擴展仿射模型相結合，提出了基于擴展仿射模型的靜態電壓穩定性全局靈敏度分析方法。經在IEEE系統中的算例分析可得如下結論：

1）基于仿射方法和擴展仿射方法建立的靜態電壓穩定性評估模型均可獲得準確的計算結果，但基于擴展仿射方法的靜態電壓穩定性評估模型比基于仿射方法的所得到的L指標區間更為精確。

2）與基于蒙特卡洛仿真的全局靈敏度分析方法相比，基于擴展仿射模型的靜態電壓穩定性全局靈敏度分析方法獲得總靈敏度指標的最大相對誤差小于11.1%，主靈敏度指標最大相對誤差指標小于9.1%，且由于解析化計算方式而具有更高計算效率。

本文建立的基于L指標的靜態電壓穩定性全局靈敏度分析方法，計算簡單且易于實現，適用于大規模風電并網后系統靜態電壓穩定性評估和靜態電壓穩定性在線快速掃描。下一步工作將考慮負荷的ZIP模型、發電機的無功限制等。

附 錄