對稱因子表的快速形成及直角坐標和極坐標PQ分解法的比較
陳 懇,丁 戈,3,唐婧璇,萬新儒
(1.南昌大學信息工程學院,江西 南昌 330031;2.江西電力職業技術學院,江西 南昌 330032;3.國網睢寧縣供電公司,江蘇 徐州 221200)
因子表法一般用于求解常系數線性方程[1-7]。不少文獻提及求取因子表時一般均采用“按行消元,逐行規格化”的過程[1,5]。對于對稱矩陣,按行消元的方式并不利于根據元素的對稱性進行計算。文獻[1-2]雖提及利用對稱性簡化下三角元素計算,或僅存儲和計算上三角元素。但在按行消元的前代計算中,獲取下三角元素并不方便,而僅存儲和使用上三角元素也會增加對對角元的反復乘除計算。此外,文獻[1-6]中都是在形成因子表后再對對角元取倒數,無形增加了程序的除法運算,降低了計算速度。
在牛頓-拉夫遜法(牛頓法)潮流計算基礎上發展起來的PQ分解法(PQ法)是電力系統中廣泛使用的潮流計算方法,其特點是將牛頓法潮流中變系數、不對稱的雅可比矩陣簡化成常系數、對稱的系數矩陣,從而將有功無功分開迭代[1-8]。然而當系統中有PV節點時,直角坐標牛頓法的方程數多于極坐標牛頓法,且前者的潮流迭代次數有時也會多于后者。但在實際潮流計算中,一般前者的計算速度快于后者,主要原因是受后者三角函數計算的影響[12]。受極坐標牛頓法的修正方程數及潮流迭代次數均少于直角坐標牛頓法等表象的影響,極坐標PQ法的應用極為廣泛,而直角坐標PQ法幾乎沒有被介紹和應用。
本文對傳統因子表的形成過程進行改進,包括:規格化前就對對角元取倒,而不是在形成因子表后才將對角元取倒;采用逐行規格化按列消元的方式、利用對稱矩陣的特點按對稱算法形成因子表。分別將這些方法用于IEEE-30~-118節點系統,可大大減少因子表的形成時間,提高計算速度。
通過比較系統中PV節點數、方程數、三角函數等對潮流迭代次數和計算速度的影響,對直角坐標和極坐標PQ分解法的計算原理進行了詳細地對比分析可發現,盡管極坐標PQ法中的方程數和迭代次數均少于直角坐標PQ法,但由于前者三角函數的計算,其潮流計算速度仍比后者慢很多。
1 對稱因子表法
1.1 按行消元形成因子表的問題
設n階線性方程組為AX=F。傳統因子表法對A陣采用“按行消元,逐行規格化”,對第k行元素消元后的A(k)′陣為式(1)。
(1)

(1)第1~k-1各行中僅一個元素與第k行中ak1~ak,k-1的一個元素對應,其對應元素的尋找、行列的變化均過于復雜。
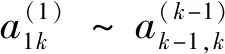
(3)由于在形成整個因子表后才將所有的對角元取倒,在其規格化計算式如式(2)中仍然有不少除法計算而影響計算速度。
(2)
1.2 按列消元形成因子表的優勢
如果對A陣采用“逐行規格化,按列消元”,且在每行元素規格化前將對角元取倒,則對第k列元素消元后得的A(k)′陣為式(3)。
(3)

(4)
(5)
比較“按行消元,逐行規格化”和“逐行規格化,按列消元”的計算過程可看出,后者在對應元素的尋找、程序中行列的變化以及元素對稱性的應用上均有極大的優勢。如果再考慮元素規格化前將對角元取倒,則還可進一步提高計算速度。實際上,在形成因子表后對F陣的前代過程中,不少文獻均采用按行消元的計算方式[4],如果該過程也用按列消元方式,同樣可大大提高計算速度。
1.3 對稱因子表法
根據式(3)可看出,“逐行規格化,按列消元”是用第k行對角元及其以右的元素對對角元以下元素進行消元。而對對稱矩陣,其第k行對角元以右的元素與第k列對角元以下的元素僅相差其對角元。因此,在形成因子表的消元計算過程中,可僅計算上三角元素,而將規格化前對角元以右元素賦值給對角元以下相應的元素獲得下三角元素。
根據上述計算規律,對稱因子表的形成過程可歸納如下:
(1)將對第k行規格化前的元素賦值給第k列對角元以下的元素,再將對角元取倒后對第k行規格化,然后對第k列元素消元,且僅計算各行中的上三角元素;
(2)將對第k+1行規格化前的元素賦值給第k+1列元素,再將對角元取倒后對第k+1行規格化,再對第k+1列元素消元,且僅計算各行的上三角元素;
(3)依此循環。
對稱因子表法是通過規格化前的上三角元素賦值得到,因而可省去所有下三角元素的計算,并由于對角元在規格化前取倒,可大大減少規格化的除法計算,從而加速因子表的形成。
1.4 對稱因子表法中四角規則應用
用四角規則可直接完成消元的前代計算而無需應用消元計算公式[13],大大簡化程序的編制。
對第k列元素消元前后其簡化矩陣如圖1所示。

用四角規則只要根據相應元素在矩陣中的位置就可直接寫出計算元素的表達式,而無需使用消元計算公式。且在對稱因子表法中,只需計算所有的上三角元素,其下三角元素可通過規格化前的元素直接賦值得到。四角規則可大大簡化編程計算。
2 極坐標與直角坐標PQ法的比較
2.1 極坐標PQ法
極坐標PQ法修正方程如式(6)、(7)。
[ΔP/V]=[B′][VΔδ]
(6)
[ΔQ/V]=[B″][ΔV]
(7)
展開式(6)、(7)可得
(8)
(9)
2.2 直角坐標PQ法
直角坐標牛頓法修正方程式如式(10)。
(10)
由于電力網絡中各元件的電抗x遠大于電阻r,因此有功功率Pi變化主要受電壓虛部fj影響,無功功率Qi和電壓幅值Vi變化主要受電壓實部ej影響,為此可略去式(10)中N、M、R子陣。再根據fi?ei、Gij?Bij,可得Gijfi≈0,并忽略接地支路。對式(10)中H、L、S子陣簡化后可得直角坐標PQ法修正方程如式(11)、(12)。
[ΔP/e]=[B′][Δf]
(11)
(12)
展開式(11)、(12)可得式(13)、(14)
(13)
(14)
2.3 極坐標與直角坐標PQ法的比較分析
雖然極坐標與直角坐標PQ法的計算原理接近,但仍有以下幾點主要不同:
(1)比較式(8)、(9)和式(13)、(14)可看出,與牛頓法類似,極坐標PQ法的方程數比直角坐標PQ法更少。
極坐標PQ法的式(8)、(9)中,B′陣為(n-1)階,B″陣為m階,且均為對稱陣;直角坐標PQ法的式(13)、(14)中,B′陣和B″陣均為(n-1)階,前者為對稱陣,后者為不對稱陣。
(2)雖然直角坐標PQ法的式(14)中階數為(n-1)階,但由于其與PV節點對應的方程中僅其對角元為-2,其它元素均為零。因此式(14)中可只對第1~m個方程消元,而對第m+1~n-1個方程無需消元。因此可將式(14)方程簡化為式(15)。
(15)

(3)分別比較式(8)、(9)和式(13)、(15)可看出,直角坐標PQ法的有功迭代過程略簡單,極坐標PQ法的無功迭代過程略簡單。
(4)極坐標PQ法中在節點電流或節點功率的計算中需使用大量三角函數,而直角坐標PQ法沒有。

3 算例分析
不考慮稀疏性時,對IEEE-30~-118節點系統用傳統因子表法、規格化之前先對對角元取倒的改進因子表法以及對稱因子表法形成因子表時間的比較結果如表1;且在均用對稱因子表法時,直角坐標PQ法和極坐標PQ法潮流的收斂時間、迭代次數等比較結果如表2。收斂判據均為ε≤10-5。

表1 不同因子表法形成時間的比較

表2 PQ法潮流計算時間和迭代次數的比較
根據表1可看出,與傳統因子表法相比,在規格化之前先對對角元取倒的改進因子表法形成因子表的速度對各個系統均可提高約4%,而用對稱因子表法形成因子表的速度隨著系統規模的增加而增加。如對IEEE-30節點系統其速度可提高約20%,而對IEEE-118節點系統可提高約35%。
根據表2可看出,雖然極坐標PQ法的迭代次數一般均少于直角坐標PQ法的迭代次數,但由于直角坐標PQ法中無三角函數的計算,其收斂所需時間反而比極坐標PQ法少很多。如IEEE-118節點系統,極坐標PQ法的迭代次數為6/5,直角坐標PQ法的迭代次數為9/8;但直角坐標PQ法收斂的計算時間僅為極坐標的32.84%,且該優勢隨著系統規模的增加而增加。因此,直角坐標PQ法比極坐標PQ法可能有更好的應用前景。
4 結論
本文在規格化之前將對角元取倒,可進一步減少除法計算;利用元素對稱性,僅計算上三角元素,下三角元素按列通過賦值上三角規格化前的元素得到,可大大提高因子表的形成速度;用四角規則可直接完成相應的消元計算,而無需應用消元計算公式,極大地便于編程。提出直角坐標PQ法,盡管其與常用的極坐標PQ法相比需求解的方程數和迭代次數更多,但由于對其方程采用特殊解法,且沒有三角函數計算,因此與極坐標PQ法相比,其潮流計算速度大大加快。且隨著系統規模的增加,優勢更加明顯。

