跳線風偏故障分析和計算方法探討

陳科技，白 航，樓文娟，張琳琳，陳賽慧

（1.國網浙江省電力有限公司經濟技術研究院，杭州 310008；2.四川省建筑科學研究院有限公司，成都 610081；3.浙江大學 建筑工程學院結構工程研究所，杭州 310058）

0 引言

跳線又稱引流線，是非直線塔（包括直線耐張塔和轉角塔）體系中桿塔兩側導線的連接線，通常分為直引跳線和繞引跳線，2 種跳線的示意圖見圖1。直引跳線如同穿過塔頭空間的一個小孤立檔導線，繞引跳線如同中間具有1（或2）個直線轉角的2（或3）個連續檔導線。輸電線路中非直線塔跳線體系的風偏研究是輸電線路風偏研究的重要內容之一，當跳線發生風偏時，會對桿塔構件形成放電，造成跳閘。故對此類跳線體系在強風場下的風偏發展情況及幅值的確定是完善輸電線路設計、保證輸電線路安全運行的重要措施。

圖1 不同種類的跳線

已有文獻表明[1-2]，由跳線風偏所引起的跳閘故障在所有風偏跳閘事故中占有較高的比例。在2005 年臺風“海棠”登陸浙江省期間，溫州地區110 kV 及以上輸電線路共發生跳閘事故67 起，其中與跳線相關的跳閘事故超過50 起[1]。2006 年6月一次颮線風引起浙江地區110 kV 輸電線路跳閘13 次、220 kV 輸電線路跳閘12 次，其中由跳線風偏引起的跳閘事故分別為5 次和7 次[1]。南方電網的事故調查及相關運行資料顯示[2]，該地區的風偏閃絡事故以耐張塔跳線風偏居多，耐張塔跳線在臺風情況下的跳閘次數占220 kV 及以上線路風偏閃絡事故的50%以上。此外，受微地形風場或短時復雜氣候條件的影響，內蒙古[3]、安徽、云南[4]、湖北[5]等非臺風多發地區的輸電線路也多次發生由跳線風偏引起的跳閘故障，跳線風偏跳閘故障已成為影響輸電線路安全穩定運行的重要因素。

輸電線路跳線風偏問題是對現有輸電線路導線風偏工況的有效補充。與普通導線相比，跳線的跨度小、質量輕、更松弛，因而在風荷載作用下更加容易產生較大的風偏位移。目前對跳線風偏的研究多集中在基于實際閃絡故障的定性分析和防治措施討論[1-6]，缺少明確的理論計算方法和計算結果討論。不同于直線塔懸垂絕緣子串的運動特性，跳線兩端的跳線絕緣子串與輸電導線直接相連，這使得跳線的風偏響應會不可避免地受到導線運動的影響，但已有的關于跳線風偏響應的研究往往忽略了上述特征[6-7]。趙雪飛[7]計算了直引跳線的風偏角并進行了輸電線路風偏風險評估分析，但并未考慮與跳線相連的導線運動對前者風偏響應的影響。考慮到繞引跳線結構形式與直線塔懸垂絕緣子線串模型相近，部分文獻[6，8]采用剛性直棒法來計算繞引跳線的風偏角，但實際上繞引跳線的運動受跳線絕緣子串、相鄰導線運動、跳線本身長度和張力、掛點高差等多因素的影響[9]，剛性直棒法并不完全適用于繞引跳線的風偏計算。為此，部分學者[10-13]討論了跳線長度的計算方法以供耐張塔塔頭設計、跳線施工安裝參考，結果表明在弧垂相同的情況下考慮跳線彎曲剛度的計算線長比不考慮時短約3.7%，但上述研究并未進一步討論跳線彎曲剛度對風偏響應的影響。此外，徐海巍等[8]采用有限元方法計算了繞引跳線在脈動風場下的動態風偏響應，但并未對直引跳線的風偏響應進行探討。錢程[14]通過縮尺模型的高頻天平測力風洞試驗測定了不同分裂數、不同形式跳線的體形系數，并運用到隨后的跳線風偏有限元計算中，但該有限元計算只對跳線本身進行了建模，并未將與之相連的導線體系納入考慮。

可以看到，現有文獻對跳線風偏響應的研究較少，對實際風偏閃絡故障中直引跳線風偏響應計算方法的討論更是罕見。為此，本文對近年來部分臺風登陸期間我國東南沿海地區輸電線路跳線風偏閃絡故障進行統計分析并總結了跳線風偏故障的易發特征；對實際故障線路進行跳線風偏響應的有限元精細化分析并確定了計算模型；以《電力工程高壓送電線路設計手冊》[9]（以下簡稱“手冊”）計算方法求解該故障塔處的跳線風偏位移并與有限元計算結果進行了對比，最后指出手冊計算方法的主要誤差來源和跳線風偏故障頻發的可能原因。

1 輸電線路跳線風偏閃絡故障統計

1.1 3 次臺風登陸期間A 市線路跳閘故障情況

近年來，在我國東南沿海地區，臺風來臨時耐張塔跳線風偏閃絡成為線路風災故障中最主要的一種形態。表1 給出了我國東南沿海地區A 市在2013 年第23 號臺風“菲特”、2015 年第13 號臺風“蘇迪羅”、2019 年第9 號臺風“利奇馬”登陸期間110～500 kV 輸電線路跳閘故障統計數據。可以看到，在臺風登陸期間跳閘線路條數與臺風登陸時的強度密切相關，臺風登陸時的最大風速越大，輸電線路發生跳閘閃絡故障越多。在單次臺風登陸過程中，輸電線路跳閘條數隨著電壓等級的提高而減少，這與不同電壓等級的輸電線路在設計校驗過程中的電氣間隙裕度和現役運行的線路數量有關。

表1 我國東南沿海A 市在臺風作用下跳閘故障統計

表2 給出了上述3 次臺風期間A 市各電壓等級輸電線路中由跳線風偏和導線風偏引起的跳閘線路統計數據。可以看出，在臺風登陸過程中500 kV 輸電線路跳閘閃絡故障均由跳線風偏引起；220 kV 輸電線路由跳線風偏和導線風偏引起的跳閘閃絡故障占比較大；110 kV 輸電線路由跳線風偏和導線風偏引起的跳閘閃絡故障占比較少，該電壓等級輸電線路在臺風登陸過程中發生跳閘閃絡事故的原因還包括倒塔、斷線、異物閃絡等。

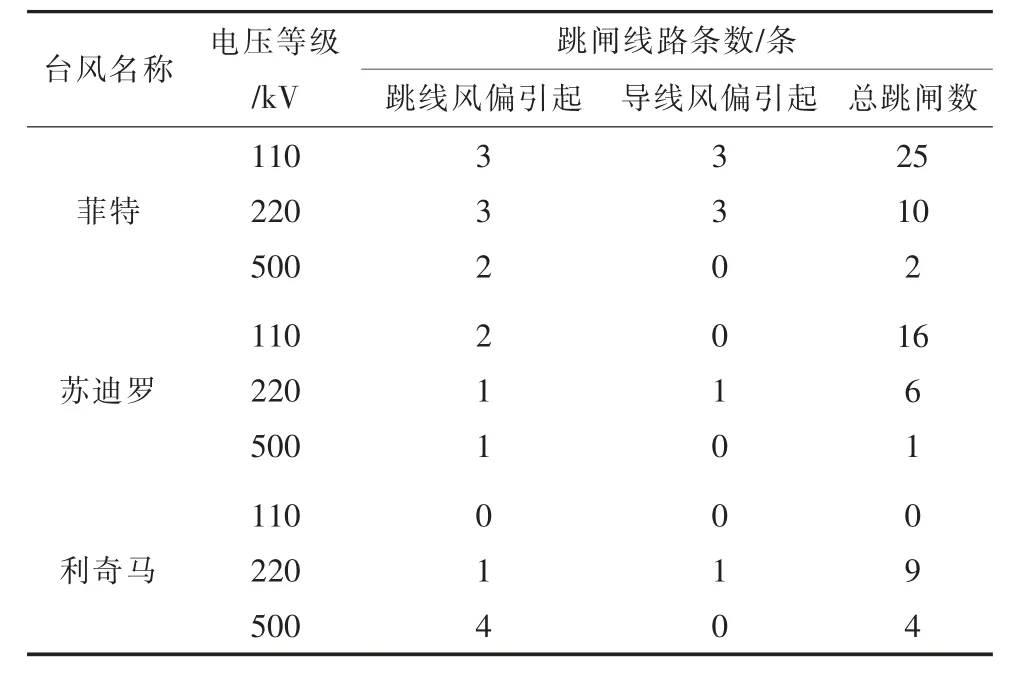
表2 3 次臺風期間A 市輸電線路風偏跳閘統計

1.2 “利奇馬”登陸期間B 市線路跳閘故障情況

表3 給出了我國東南沿海另一城市B 市在2019 年第9 號臺風“利奇馬”登陸期間110～500 kV輸電線路跳閘統計數據，其中220 kV 線路已明確故障原因的跳閘次數為33 次（共66 次），500 kV 線路15 次跳閘的故障原因已全部查明，對應的故障原因統計見圖2。

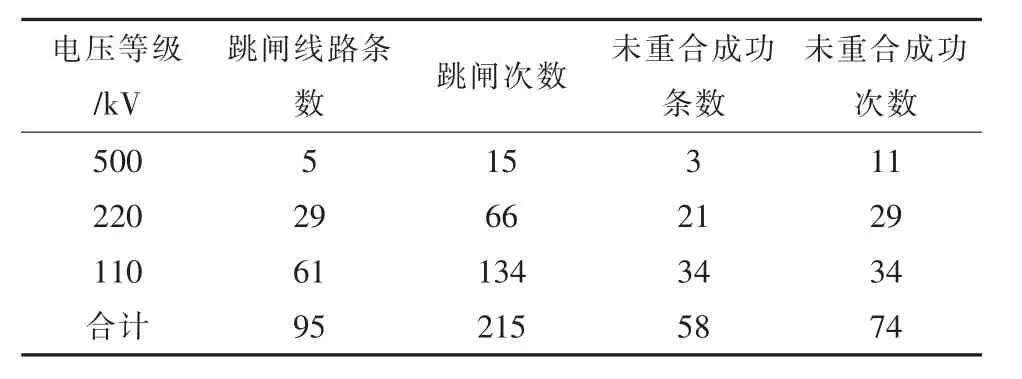
表3 臺風“利奇馬”登陸期間B 市輸電線路跳閘故障統計

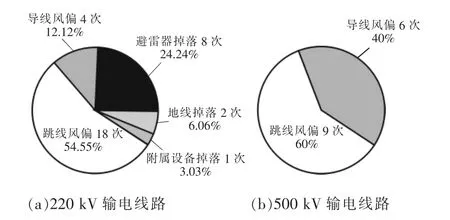
圖2 “利奇馬”登陸期間B 市跳閘線路故障原因統計

可以看出，在“利奇馬”登陸期間，B 市不同電壓等級輸電線路跳閘條數和次數也隨著電壓等級的提高而減少，而由跳線風偏和導線風偏引起的跳閘閃絡故障在220 kV 輸電線路的總跳閘故障中（已明確故障原因部分）同樣占比較大，兩者之和達到了66.67%。與A 市不同的是，B市500 kV輸電線路的跳閘閃絡故障由跳線風偏和導線風偏共同引起，但由跳線風偏引起的仍達到了60%，跳線風偏仍是引起這一電壓等級輸電線路跳閘閃絡故障的主要原因。同時從表3 可以看出，臺風登陸期間220 kV 和500 kV 輸電線路發生跳閘閃絡故障時具有重合成功條數低的特點，兩者重合成功的線路條數僅占27.59%和40%。

1.3 “黑格比”登陸期間A 市、B 市線路跳閘故障情況

作為補充，表4 給出了2020 年第4 號臺風“黑格比”登陸期間A 市、B 市兩地部分輸電線路跳閘閃絡情況。由于“黑格比”登陸時間較近，目前缺少該次臺風登陸期間A 市、B 市兩地不同電壓等級輸電線路跳閘閃絡故障的完整統計數據，表4 僅給出了目前已知的8 條220 kV 和500 kV輸電線路跳閘閃絡故障概況。可以發現，已有資料的8 條跳閘線路閃絡故障均由跳線風偏或導線風偏造成，其中有6 條跳閘線路（500 kV 線路和220 kV 線路各3 條）的故障原因與跳線風偏有關。同時，跳閘線路重合成功率低的特點也在本次臺風登陸過程中得到了印證。

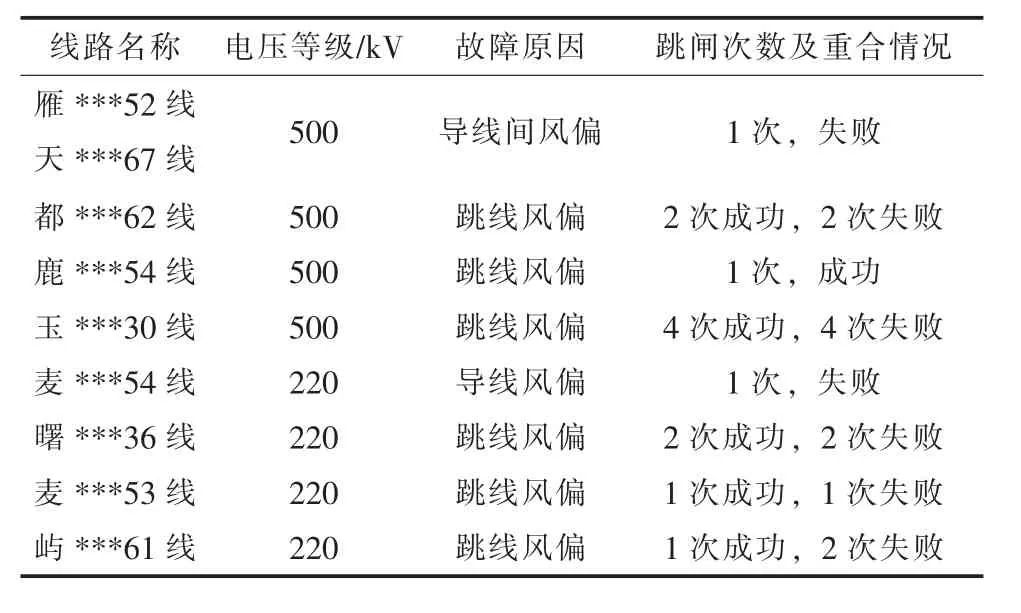
表4 A 市、B 市兩地在臺風“黑格比”登陸期間部分線路跳閘故障概況

對上述臺風登陸期間A 市、B 市兩地由跳線風偏引起的220 kV 和500 kV 輸電線路跳閘閃絡故障中故障桿塔所處地理位置進行分析統計，發現所有跳閘閃絡故障的故障桿塔均處于山地地區或沿海小平原邊緣的丘陵地區，受微地形效應的影響較為顯著。

綜上可知，近年來我國東南沿海地區220 kV及以上輸電線路跳閘閃絡故障多由跳線風偏和導線風偏引起，其中跳線風偏已成為500 kV 輸電線路跳閘閃絡故障的最主要原因。由跳線風偏引起的輸電線路跳閘閃絡故障呈現出重合率低的特點，且發生跳線風偏閃絡的故障桿塔均處于山地丘陵地區。

2 典型跳線風偏閃絡故障簡介

2020 年第4 號臺風“黑格比”于8 月4 日凌晨3:30 在浙江樂清登陸，中心最大風力13 級，登陸期間附近多個氣象站偵測到最大風速大于38 m/s。某220 kV 輸電線路在8 月4 日2:30—3:10共發生3 次故障跳閘，其中1 次重合成功，2 次重合失敗。臺風過后巡視人員對故障區段進行檢查，發現該輸電線路第一次跳閘因為47 號塔A相跳線風偏，第二、三次跳閘因為91 號塔A 相、B 相跳線風偏。以47 號桿塔為例，圖3 給出了其A 相跳線和塔身處的放電痕跡。

圖3 某220 kV 線路跳線風偏故障照片

某500 kV 輸電線路于8 月4 日2:39—6:14在3 處不同位置處共發生4 次故障跳閘，其中2次重合成功，2 次重合失敗。8 月5 日特巡檢查發現該輸電線路33 號桿塔和38 號桿塔的A 相跳線和塔身均有明顯放電痕跡，而107 號桿塔的A相跳線、C 相跳線及對應塔身位置有明顯放電痕跡。以33 號桿塔為例，圖4 給出了其A 相跳線和塔身處的放電痕跡及可能的放電通道。

圖4 某500 kV 線路33 號塔處跳線風偏故障照片

3 跳線風偏響應有限元計算

3.1 跳線風偏響應有限元計算模型

與輸電導線的風偏響應分析類似，對轉角塔跳線系統的風偏響應可以采用基于有限元模型的動力時程分析計算方法。但由于轉角塔跳線系統在風荷載作用下的風偏發展情況不僅與跳線本身的位移響應密切相關，還將受到跳線兩端導線運動的顯著影響，因此，考慮導線影響的轉角塔跳線風偏計算模型的建立是跳線風偏響應有限元計算中的關鍵步驟。

以前文中發生跳線風偏閃絡故障的某500 kV 輸電線路33 號塔為中心，建立了其左右2 個耐張段之間總計7 塔6 檔線路和跳線體系有限元模型。33 號塔型號為JTS1（24），桿塔海拔104.3 m，呼高30 m。33 號塔處線路轉角27°18′，其線路如圖5 所示，圖中括號內的數字為導線懸掛點的離地高度，單位為m。線路導線和跳線型號均為四分裂LGJ630/45，跳線系統位于33 號耐張塔處，其檔距約為16.68 m。由圖4 可知發生閃絡的跳線為直引跳線，因此本文后續均以直引跳線為研究對象。

圖5 故障線路兩耐張段示意

在實際ANSYS 建模過程中，采用等效單導線模型來模擬實際的四分裂導線，導線及耐張段絕緣子均采用Link10 單元模擬；直線塔及繞引跳線處懸式復合絕緣子采用Link8 單元模型，單元一端鉸接于導線相應位置，另一端則鉸接于固定支座上，跳線采用Beam188 單元模型，同時采用Mass21 單元模擬跳線相應位置處的間隔棒質量。跳線段端部節點與多跨導線相應位置的節點采用耦合三維平動位移并約束轉角位移的方式來模擬實際的連接方式。

為考察各因素對轉角塔跳線串結構風偏作用的影響，在整體多跨導線體系轉角塔跳線風偏發展情況的基礎上，提出了以下計算模型：

（1）考慮前述2 個耐張段之間全部的7 塔6檔線路及相鄰耐張段之間的轉角塔跳線體系，本文稱之為全跨模型。

（2）為考察導線線路跨數對跳線結構的影響，只取33 號耐張塔為中心的前后各一跨導線，即32—34 號桿塔之間3 塔2 檔導線及跳線耦合連接體系，本文稱之為耦聯模型。

（3）為考察跳線結構的實際運動方式并確認跳線風偏的貢獻主要來自多跨導線的整體運動對其的激勵還是跳線本身的平面外擺動，建立了孤立的跳線結構模型，其中跳線兩端部節點自由度全部約束，本章稱之為孤立模型。

直引跳線的3 種計算模型簡圖和坐標軸方向如圖6 所示，全局坐標系O-XYZ 的X 軸與33—37 號桿塔區間的線路走向平行，Z 軸豎直向上；而跳線局部坐標系O-X′Y′Z′的X′軸與跳線懸掛點A，B 的連線方向平行，Z′軸同樣豎直向上。

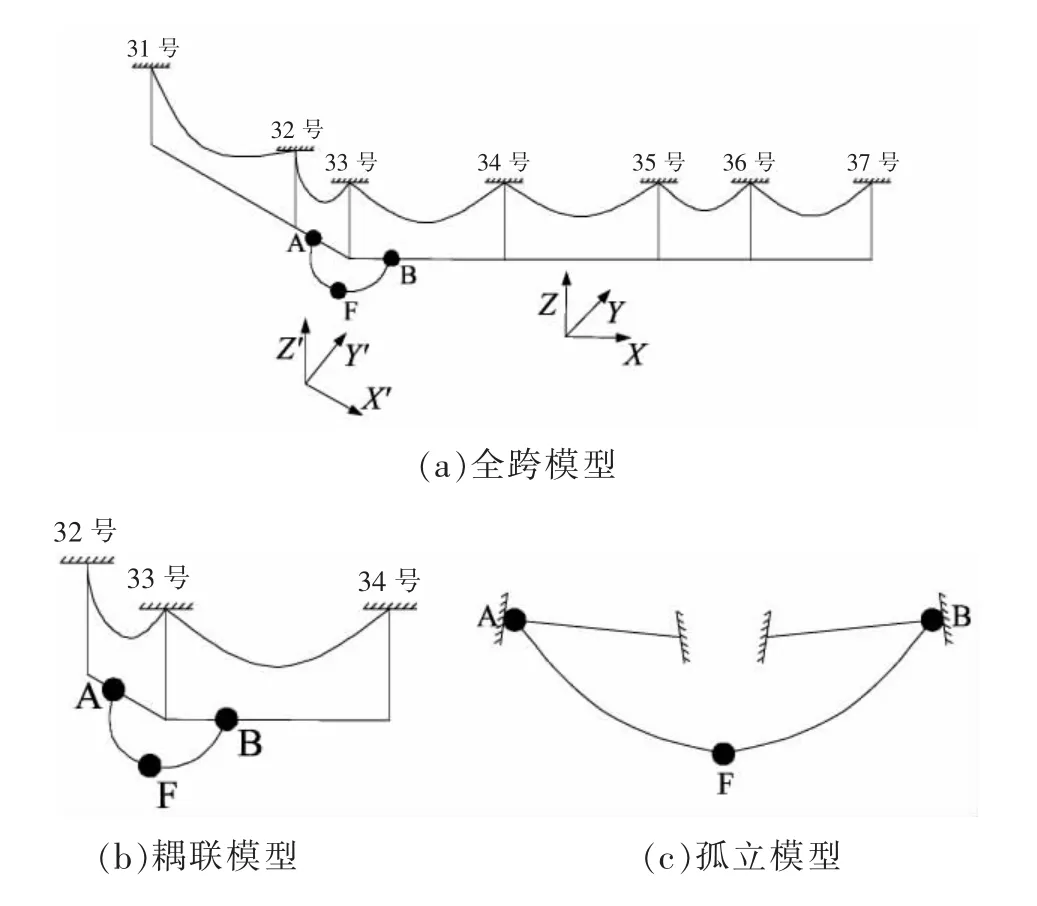
圖6 直引跳線的有限元模型示意

3.2 跳線風偏響應有限元計算結果

采用時域法對上述3 種跳線計算模型進行風偏響應有限元計算，其中輸電線路導線和跳線的多點同步風荷載可采用諧波疊加法來進行模擬。計算時考慮線路處于B 類平坦地貌，基本風速U0=27 m/s，來流方向與全局坐標系的Y 軸正方向相同，即在水平面內垂直于33—37 號桿塔區間的線路走向，時間間隔取Δt=0.062 5 s，模擬時長T=2 048 s，風速譜采用Davenport 譜。需要說明的是，若直接采用突加荷載的形式將風荷載時程施加于整體輸電線路結構上，則風偏響應時域計算的初始階段風致響應會出現與真實情況不符的大幅瞬態沖擊響應。為消除該影響，在風速時程前段加入時長100 s 的由0 m/s 增至平均風速的線性增長過程。該過程相較于全時程2 148 s 的動態荷載施加過程比例較小，基本不會影響風偏量值的合理分布，并能有效消除突加荷載的影響。

本文以弧垂最低點F 處的風偏位移來表征直引跳線的風偏響應。表5 給出了F 點以及跳線懸掛點A 點、B 點的風偏位移有限元計算結果。由于采用孤立模型計算時跳線懸掛點A 點、B 點為固定鉸支座（如圖6 所示），兩點的風偏位移均為0，因此表5 僅給出了全跨模型和耦聯模型的A點、B 點位移計算結果。

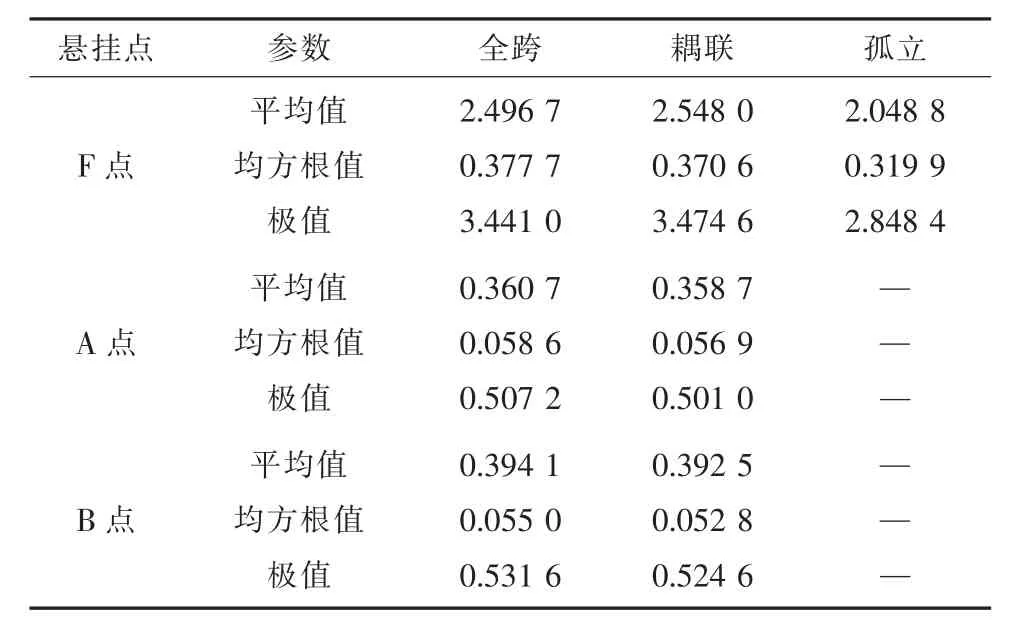
表5 故障線路跳線Y′向風偏位移結果 m

可以看到，該故障塔處直引跳線的風偏位移結果雖以平均位移為主，但其脈動位移也不可忽略，這與導線的風偏位移結果類似。從計算模型的角度分析，全跨模型在3 個點處的風偏位移均值和極值與耦聯模型均非常接近，耦聯模型能準確反映跳線的實際風偏情況，并可減少計算量和加快運行速度，最適用于有限元分析計算。孤立模型的風偏位移均值和極值相較于前兩者明顯偏小，這說明忽略跳線兩端導線作用計算得到的跳線風偏位移是偏于不安全的，但耦聯模型和全跨模型的風偏位移在平均值和極值方面仍是以孤立模型的貢獻為主。由于跳線運動與導線運動之間的相互作用，全跨模型或耦聯模型的風偏位移并不是孤立模型與跳線懸掛點風偏位移的簡單求和。

4 跳線風偏響應的手冊計算方法誤差分析

現行手冊給出了直引跳線的風偏位移計算公式。考慮到直引跳線的懸掛點位置（即耐張絕緣子串尾部）會隨兩側導線的運動而改變，因此其總的順風向風偏位移DH可以看作跳線兩側懸掛點在風荷載作用下的平均水平位移Δecp與跳線本身的順風向風偏位移Dt兩部分之和。

本文仍以圖5 所示的故障線路和計算參數為例，采用手冊計算方法對33 號桿塔處的直引跳線順風向風偏位移進行計算，表6 給出了直引跳線風偏手冊方法計算結果與有限元靜力計算結果的對比。可以看到，手冊方法對直引跳線孤立模型部分的風偏位移均值Dt的計算較準，但在一定程度上低估了跳線懸掛點的平均風偏位移Δecp，這是直引跳線手冊計算方法誤差來源之一。手冊方法直接將Dt和Δecp兩部分位移相加得到直引跳線的風偏總位移，而從有限元結果可以看到直引跳線F 點的風偏位移并不等于孤立模型風偏位移與A 點、B 點風偏位移之和。作為參考，表6中給出了全跨模型名義上的Dt結果（以* 表示），可以看到該結果與孤立模型的Dt并不相等。手冊采用兩部分直接相加的計算方法會在一定程度上低估直引跳線的風偏位移。以上兩部分誤差皆由手冊方法的計算模型引起，因此統稱為模型誤差。事實上，直引跳線手冊計算方法的模型誤差對計算結果的影響較為有限，在數值上約為5%。忽略了脈動風的放大效應才是直引跳線手冊計算方法結果偏小的根本原因。表7 給出了直引跳線風偏手冊方法計算結果與有限元動力計算結果的對比。可以看到，全跨模型的有限元風偏位移極值是手冊方法計算結果的1.45 倍，該放大系數綜合考慮了模型誤差及脈動風的放大作用。若扣除模型誤差5%的影響，可得脈動風對跳線風偏響應的放大系數達到了1.38。

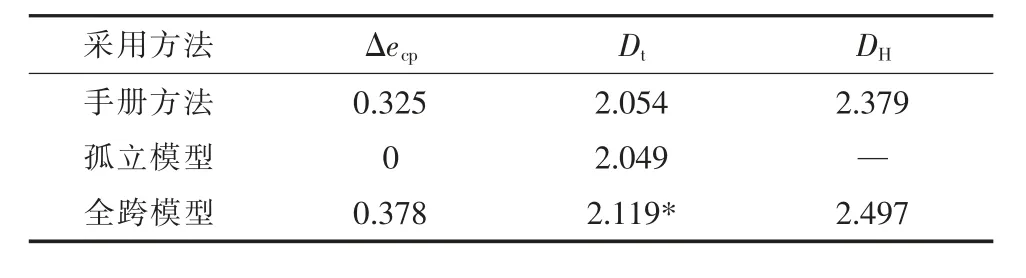
表6 直引跳線風偏手冊方法與有限元靜力結果對比m

表7 直引跳線風偏手冊方法與有限元動力結果對比

根據手冊方法和有限元計算的結果對比可知，由于忽略了脈動風的放大作用以及客觀存在的模型誤差，手冊方法會嚴重低估輸電線路跳線風偏響應。在輸電線路設計和校驗時，采用手冊方法會造成線路電氣間隙裕度不足，這也是輸電線路跳線風偏閃絡故障頻發的原因之一。

作為補充，圖7 給出了不同基本風速下33號桿塔處的跳線風偏位移結果。可以看到，在設計風速（39 m/s）條件下33 號桿塔處按照手冊計算方法得到的風偏位移結果約為3.5 m。實際上，有限元分析方法在基本風速為27 m/s 時的計算結果已與之接近，即按照設計風速39 m/s 設計的線路在實際風速為27 m/s 時就可能發生閃絡故障，這也從側面反映出了手冊計算方法對脈動風放大作用的考慮不足。

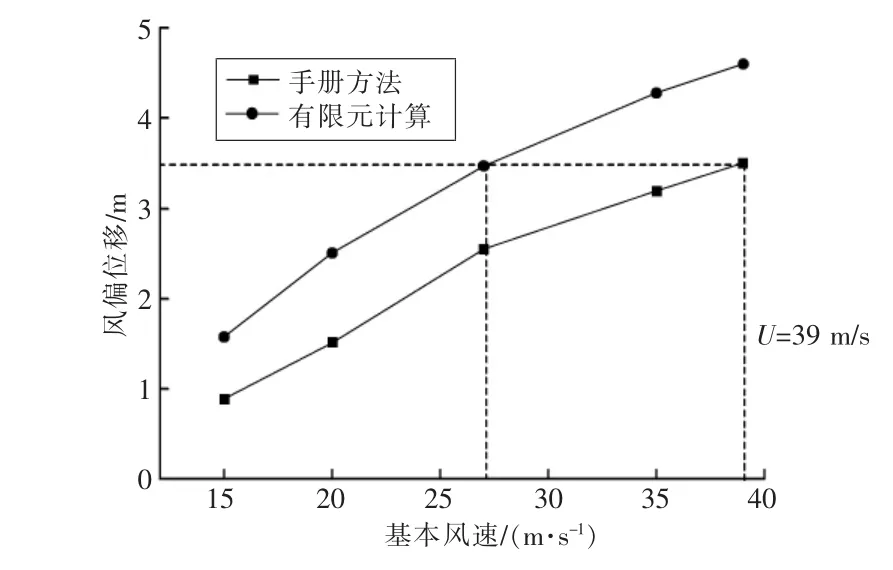
圖7 直引跳線風偏位移隨風速的變化規律

5 結論

本文對近年來部分臺風登陸期間我國東南沿海地區輸電線路跳線風偏閃絡故障特征進行了統計分析；對實際故障線路進行跳線風偏響應的有限元精細化分析并確定了計算模型；以現行手冊計算方法求解故障塔處的跳線風偏位移并與有限元計算結果進行對比，指出手冊計算方法的主要誤差來源和跳線風偏故障頻發的可能原因。主要結論如下：

（1）跳線風偏已成為近年來我國東南沿海地區輸電線路跳閘閃絡故障的最主要原因，跳線風偏引起的輸電線路跳閘閃絡故障呈現出重合率低的特點，且發生跳線風偏閃絡的故障桿塔多處于山地丘陵地區。

（2）與跳線相連的導線運動對跳線風偏響應有較為明顯的影響，取耐張塔前后各一跨導線及跳線結構的耦聯模型能準確反映跳線的實際風偏情況并減少計算量，其計算結果與全跨模型一致。

（3）脈動風對跳線風偏響應的放大系數約為1.38，由于未考慮脈動風的放大作用以及客觀存在的模型誤差，現行手冊計算方法得到的跳線風偏位移要明顯小于有限元計算結果，這也是輸電線路跳線風偏閃絡故障頻發的主要原因之一。